5.1.1: Entradas y Salidas
- Page ID
- 118594
Lección
Hagamos algunas reglas.
Ejercicio\(\PageIndex{1}\): Dividing by 0
Estudie cuidadosamente las declaraciones.
- \(12\div 3=4\)porque\(12=4\cdot 3\)
- \(6\div 0=x\)porque\(6=x\cdot 0\)
¿Qué valor se puede utilizar en lugar de\(x\) crear declaraciones verdaderas? Explica tu razonamiento.
Ejercicio\(\PageIndex{2}\): Guess My Rule
Intenta averiguar qué está pasando en la “caja negra”.
Nota: Debes presionar enter o return antes de hacer clic en GO.
¿Estás listo para más?
Si tienes una regla, puedes aplicarla varias veces seguidas y buscar patrones. Por ejemplo, si tu regla era “agregar 1" y empezaste con el número 5, entonces al aplicar esa regla una y otra vez obtendrías 6, luego 7, luego 8, etc., formando un patrón obvio.
Prueba esto por las reglas en esta actividad. Es decir, comenzar con el número 5 y aplicar cada una de las reglas varias veces. ¿Notaste algún patrón? ¿Y si comienzas con un número inicial diferente?
Ejercicio\(\PageIndex{3}\): Making Tables
Para cada regla de entrada-salida, rellena la tabla con las salidas que van con una entrada dada. Agrega dos pares de entrada-salida más a la tabla.
1.

| entrada | salida |
|---|---|
| \(\frac{3}{4}\) | \(7\) |
| \(2.35\) | |
| \(42\) | |
2.

| entrada | salida |
|---|---|
| \(\frac{3}{4}\) | \(7\) |
| \(2.35\) | |
| \(42\) | |
3.
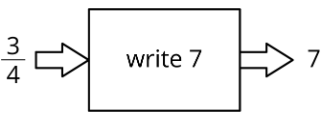
| entrada | salida |
|---|---|
| \(\frac{3}{4}\) | \(7\) |
| \(2.35\) | |
| \(42\) | |
Haz una pausa aquí hasta que tu profesor te dirija a la última regla.
4.

| entrada | salida |
|---|---|
| \(\frac{3}{7}\) | \(\frac{7}{3}\) |
| \(1\) | |
| \(0\) | |
Resumen
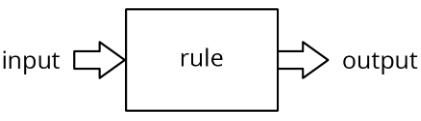
Una regla de entrada-salida es una regla que toma una entrada permisible y la usa para determinar una salida. Por ejemplo, el siguiente diagrama representa la regla que toma cualquier número como entrada, luego agrega 1, multiplica por 4 y da el número resultante como salida.

En algunos casos, no todas las entradas son permisibles, y la regla debe especificar qué entradas funcionarán. Por ejemplo, esta regla está bien cuando la entrada es 2:

Pero si la entrada es -3, necesitaríamos evaluar\(6\div 0\) para obtener la salida.

Entonces, cuando decimos que la regla es “dividir 6 por 3 más que la entrada”, también tenemos que decir que -3 no está permitido como entrada.
Práctica
Ejercicio\(\PageIndex{4}\)
Dada la regla:

Complete la tabla para la regla de función para los siguientes valores de entrada:
| entrada | 0 | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|
| salida |
Ejercicio\(\PageIndex{5}\)
Aquí hay una regla de entrada y salida:

Complete la tabla para la regla de entrada y salida:
| entrada | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| salida |
Ejercicio\(\PageIndex{6}\)
La escuela de Andre ordena algunos suministros nuevos para el laboratorio de química. La tienda en línea muestra un paquete de 10 tubos de ensayo cuesta $4 menos que un juego de vasos de precipitados anidados. Para equipar completamente el laboratorio, la escuela ordena 12 juegos de vasos de precipitados y 8 paquetes de tubos de ensayo.
- Escribir una ecuación que muestre el costo de un paquete de tubos de ensayo,\(t\), en términos del costo de un conjunto de vasos de precipitados,\(b\).
- La oficina de la escuela recibe una factura por los suministros por un monto de 348 dólares. Escribe una ecuación con\(t\) y\(b\) que describa esta situación.
- Ya que\(t\) es en términos de\(b\) desde la primera ecuación, esta expresión puede ser sustituida por la segunda ecuación donde\(t\) aparece. Escribe una ecuación que muestre esta sustitución.
- Resolver la ecuación para\(b\).
- ¿Cuánto pagó la escuela por un juego de vasos de precipitados? ¿Para un paquete de tubos de ensayo?
(De la Unidad 4.3.6)
Ejercicio\(\PageIndex{7}\)
Resolver:
\[\left\{\begin{array}{l}{y=x-4}\\{y=6x-10}\end{array}\right.\nonumber\]
Ejercicio\(\PageIndex{8}\)
¿Por qué valor de\(x\) las expresiones\(2x+3\) y\(3x-6\) tienen el mismo valor?
(De la Unidad 4.2.8)


