5.2.5: Conexión de representaciones de funciones
- Page ID
- 118603
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Conectemos tablas, ecuaciones, gráficas e historias de funciones.
Ejercicio\(\PageIndex{1}\): Which are the Same? Which are Different?
Aquí hay tres formas diferentes de representar funciones. ¿Cómo son iguales? ¿En qué se diferencian? \(y=2x\)
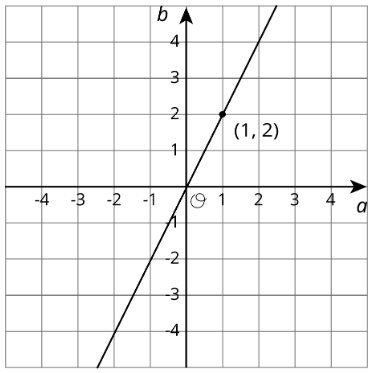
| \(p\) | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| \(q\) | 4 | 2 | 0 | -2 | -4 | -6 |
Ejercicio\(\PageIndex{2}\): Comparing Temperatures
El gráfico muestra la temperatura entre el mediodía y la medianoche en Ciudad A en un día determinado.
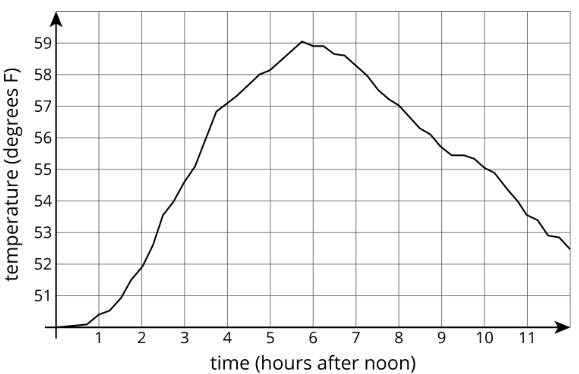
En la tabla se muestra la temperatura\(T\), en grados Fahrenheit, para\(h\) horas después del mediodía, en la Ciudad B.
| \(h\) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| \(T\) | 82 | 78 | 75 | 62 | 58 | 59 |
- ¿Qué ciudad era más cálida a las 4:00 p.m.?
- ¿Qué ciudad tuvo un mayor cambio de temperatura entre la 1:00 p.m. y las 5:00 p.m.?
- ¿Cuánto mayor fue la temperatura más alta registrada en Ciudad B que la temperatura más alta registrada en Ciudad A durante este tiempo?
- Compara las salidas de las funciones cuando la entrada es 3.
Ejercicio\(\PageIndex{3}\): Comparing Volumes
El volumen,\(V\), de un cubo con longitud de borde\(s\) cm viene dado por la ecuación\(V=s^{3}\). El volumen de una esfera es función de su radio (en centímetros), y aquí se muestra la gráfica de esta relación.
- ¿El volumen de un cubo con longitud de borde es\(s=3\) mayor o menor que el volumen de una esfera con radio 3?
- Si una esfera tiene el mismo volumen que un cubo con una longitud de borde 5, estime el radio de la esfera.
- Compara las salidas de las dos funciones de volumen cuando las entradas son 2.
Aquí hay un applet para usar si así lo desea.
¿Estás listo para más?
Estime la longitud de borde de un cubo que tiene el mismo volumen que una esfera con radio 2.5.
Ejercicio\(\PageIndex{4}\): It's Not a Race
La familia de Elena conduce por la autopista a 55 millas por hora.
La familia de Andre circula por la misma autopista, pero no a una velocidad constante. En la tabla se muestra hasta dónde ha viajado la familia de Andre\(d\),, en millas, cada minuto durante 10 minutos.
| \(t\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(d\) | 0.9 | 1.9 | 3.0 | 4.1 | 5.1 | 6.2 | 6.8 | 7.4 | 8 | 9.1 |
- ¿Cuántas millas por minuto son 55 millas por hora?
- ¿Quién había viajado más lejos después de 5 minutos? ¿Después de 10 minutos?
- ¿Cuánto tardó la familia de Elena en viajar tan lejos como la familia de Andre había viajado después de 8 minutos?
- Para ambas familias, la distancia en millas es una función del tiempo en minutos. Compara las salidas de estas funciones cuando la entrada es 3.
Resumen
Las funciones se tratan de obtener salidas de entradas. Para cada forma de representar una función —ecuación, gráfica, tabla o descripción verbal— podemos determinar la salida para una entrada dada.
Digamos que tenemos una función representada por la ecuación\(y=3x+2\) donde\(y\) está la variable dependiente y\(x\) es la variable independiente. Si quisiéramos encontrar la salida que va con 2, podemos ingresar 2 en la ecuación para\(x\) y encontrar el valor correspondiente de\(y\). En este caso, cuando\(x\) es 2,\(y\) es 8 ya que\(3\cdot 2+2=8\).
Si en su lugar tuviéramos una gráfica de esta función, entonces las coordenadas de los puntos en la gráfica son los pares entrada-salida. Entonces leeríamos la\(y\) coordenada -del punto en la gráfica que corresponde a un valor de 2 para\(x\). Al mirar la gráfica de esta función aquí, podemos ver el punto\((2,8)\) en ella, por lo que la salida es 8 cuando la entrada es 2.
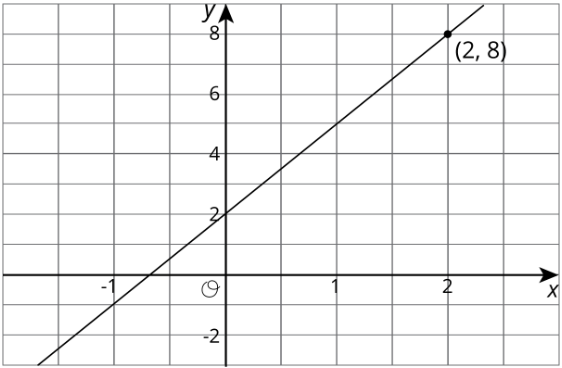
Una tabla que representa esta función muestra los pares entrada-salida directamente (aunque solo para entradas seleccionadas).
| \(x\) | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| \(y\) | -1 | 2 | 5 | 8 | 11 |
Nuevamente, la tabla muestra que si la entrada es 2, la salida es 8.
Entradas en el glosario
Definición: Variable dependiente
Una variable dependiente representa la salida de una función.
Por ejemplo, supongamos que necesitamos comprar 20 piezas de fruta y decidir comprar manzanas y plátanos. Si seleccionamos primero el número de manzanas, la ecuación\(b=20-a\) muestra el número de plátanos que podemos comprar. El número de plátanos es la variable dependiente porque depende del número de manzanas.
Definición: Variable independiente
Una variable independiente representa la entrada de una función.
Por ejemplo, supongamos que necesitamos comprar 20 piezas de fruta y decidir comprar algunas manzanas y plátanos. Si seleccionamos primero el número de manzanas, la ecuación\(b=20-a\) muestra el número de plátanos que podemos comprar. El número de manzanas es la variable independiente porque podemos elegir cualquier número para ello.
Definición: Radio
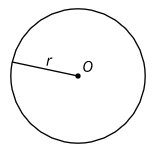
Un radio es un segmento de línea que va desde el centro hasta el borde de un círculo. Un radio puede ir en cualquier dirección. Cada radio del círculo tiene la misma longitud. También usamos la palabra radio para significar la longitud de este segmento.
Por ejemplo,\(r\) es el radio de este círculo con centro\(O\).
Definición: Volumen
Volumen es el número de unidades cúbicas que llenan una región tridimensional, sin huecos ni superposiciones.
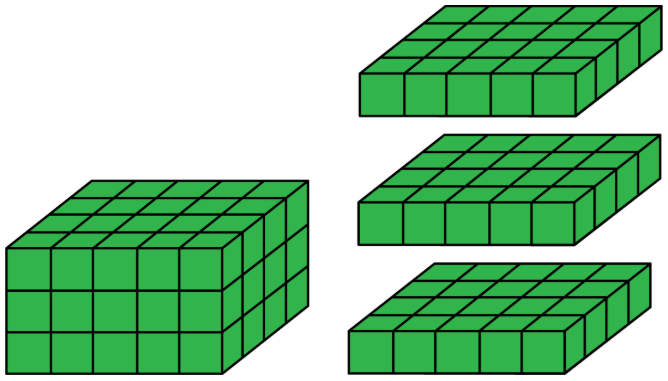
Por ejemplo, el volumen de este prisma rectangular es de 60 unidades 3, debido a que está compuesto por 3 capas que son cada una de 20 unidades 3.
Practica
Ejercicio\(\PageIndex{5}\)
La ecuación y las tablas representan dos funciones diferentes. Usa la ecuación\(b=4a-5\) y la tabla para responder a las preguntas. Esta tabla representa\(c\) como una función de\(a\).
| \(a\) | -3 | 0 | 2 | 5 | 10 | 12 |
|---|---|---|---|---|---|---|
| \(c\) | -20 | 7 | 3 | 21 | 19 | 45 |
- ¿Cuándo\(a\) es -3, es\(b\) o\(c\) mayor?
- Cuando\(c\) es 21, ¿cuál es el valor de\(a\)? ¿Cuál es el valor de\(b\) que va con este valor de\(a\)?
- ¿Cuándo\(a\) es 6, es\(b\) o\(c\) mayor?
- ¿Para qué valores de\(a\) sabemos que\(c\) es mayor que\(b\)?
Ejercicio\(\PageIndex{6}\)
Elena y Lin están entrenando para una carrera. Elena corre su milla a una velocidad constante de 7.5 millas por hora.
Las distancias totales de Lin se registran cada minuto:
| tiempo (minutos) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| distancia (millas) | 0.11 | 0.21 | 0.32 | 0.41 | 0.53 | 0.62 | 0.73 | 0.85 | 1 |
- ¿Quién terminó primero su milla?
- Esta es una gráfica del progreso de Lin. Dibuja una gráfica para representar la milla de Elena en los mismos ejes.
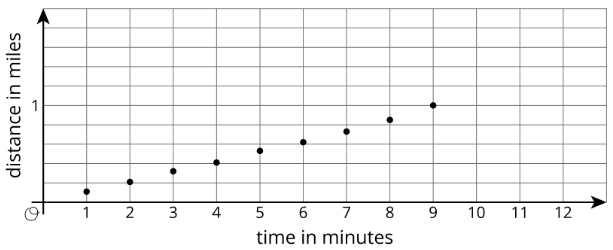
3. Para estos modelos, ¿la distancia es una función del tiempo? ¿El tiempo es una función de la distancia? Explique cómo sabe.
Ejercicio\(\PageIndex{7}\)
Haga coincidir cada regla de función con el valor que no podría ser una entrada posible para esa función.
- 3 dividido por la entrada
- Agrega 4 a la entrada, luego divide este valor en 3
- Restar 3 de la entrada, luego dividir este valor en 1
- 3
- 4
- -4
- 0
- 1
(De la Unidad 5.1.2)
Ejercicio\(\PageIndex{8}\)
Encontrar un valor\(x\) que haga que la ecuación sea verdadera. Explica tu razonamiento, y comprueba que tu respuesta sea correcta.
\(-(-2x+1)=9-14x\)
(De la Unidad 4.2.3)