5.3.3: Funciones lineales por piezas
- Page ID
- 118621
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Exploremos funciones construidas a partir de piezas lineales.
Ejercicio\(\PageIndex{1}\): Notice and Wonder: Lines on Dots
¿Qué notas? ¿Qué te preguntas?
Ejercicio\(\PageIndex{2}\): Modeling Recycling
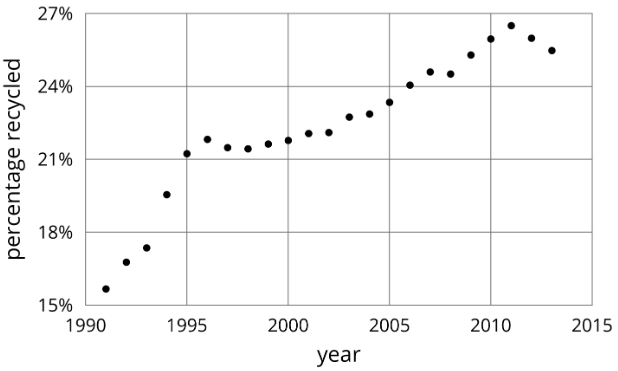
- Aproximar el porcentaje reciclado cada año con una función lineal por tramos dibujando entre tres y cinco segmentos de línea para aproximar la gráfica.
- Encuentra la pendiente para cada pieza. ¿Qué te dicen estas pendientes?
Ejercicio\(\PageIndex{3}\): Dog Bath
Elena llenó la bañera y le dio un baño a su perro. Después dejó salir el agua de la tina.
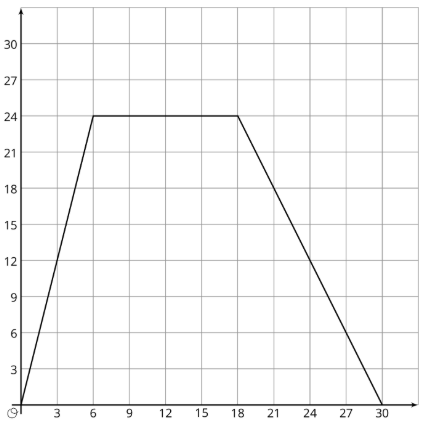
- El gráfico muestra la cantidad de agua en la tina, en galones, en función del tiempo, en minutos. Agrega etiquetas a la gráfica para mostrar esto.
- ¿Cuándo apagó el grifo de agua?
- ¿Cuánta agua había en la tina cuando bañaba a su perro?
- ¿Cuánto tiempo tardó en drenar completamente la tina?
- ¿A qué ritmo el grifo llenó la tina?
- ¿A qué ritmo se drenó el agua de la tina?
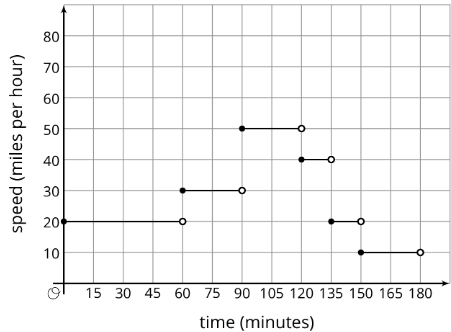
Ejercicio\(\PageIndex{4}\): Distance and Speed
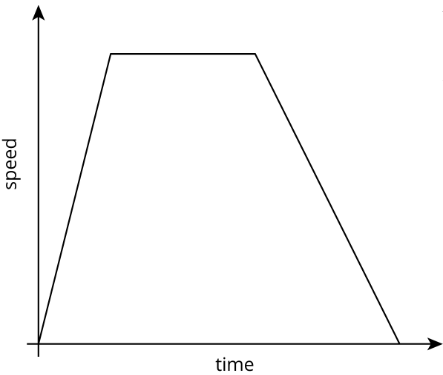
El gráfico muestra la velocidad de un automóvil en función del tiempo. Describe lo que vería una persona que vigila el auto.
¿Estás listo para más?
El gráfico modela la velocidad de un automóvil en función del tiempo durante un viaje de
3 horas. ¿Hasta dónde llegó el auto en el transcurso del viaje?
Hay una buena manera de visualizar esta cantidad en términos de la gráfica. ¿Lo puedes encontrar?
Resumen
Esta gráfica muestra a Andre en bicicleta hasta la casa de su amigo donde pasa el rato por un tiempo. Después van en bicicleta juntos a la tienda para comprar algunos comestibles antes de correr de regreso a la casa de Andre para una noche de cine. Cada segmento de línea en la gráfica representa una parte diferente de los viajes de Andre.
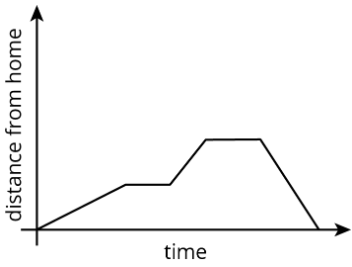
Este es un ejemplo de una función lineal por tramos, que es una función cuya gráfica se reconstruye a partir de segmentos de línea. Se puede utilizar para modelar situaciones en las que una cantidad cambia a una tasa constante por un tiempo, luego cambia a una tasa constante diferente.
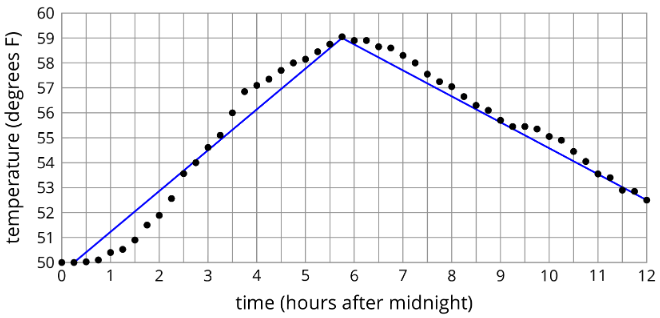
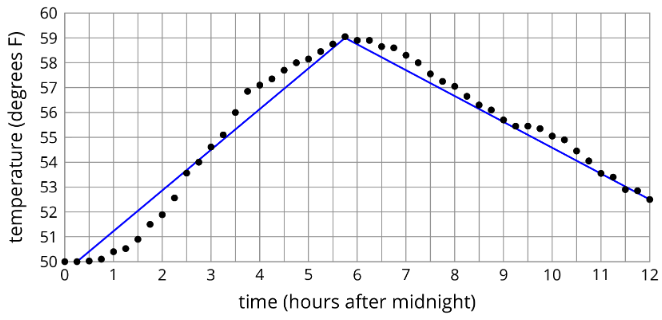
Podemos usar funciones por partes para representar historias, o podemos usarlas para modelar datos reales. En el segundo ejemplo, los registros de temperatura en varias ocasiones a lo largo del día se modelan con una función por tramos compuesta por dos segmentos de línea. ¿Qué segmento de línea crees que hace el mejor trabajo de modelar los datos?
Practica
Ejercicio\(\PageIndex{5}\)
El gráfico muestra la distancia de un automóvil desde su casa en función del tiempo.
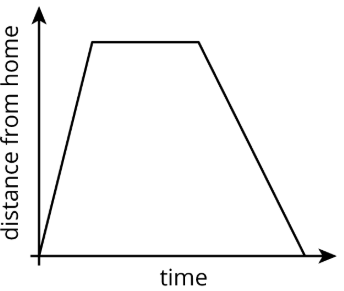
Describa lo que puede estar viendo una persona que vigila el auto.
Ejercicio\(\PageIndex{6}\)
La ecuación y la gráfica representan dos funciones. Usa la ecuación\(y=4\) y la gráfica para responder a las preguntas.
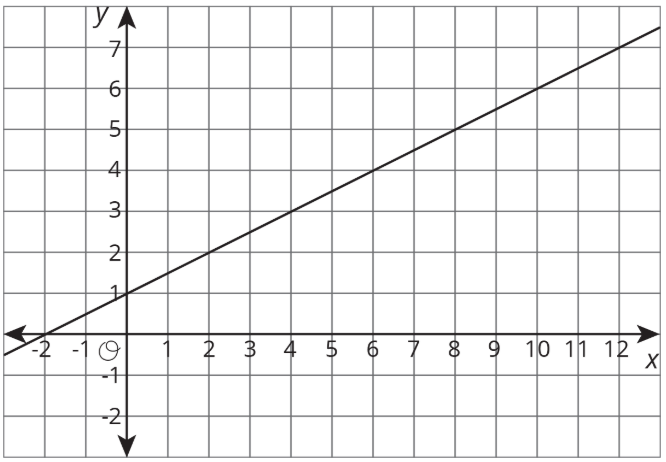
- Cuando\(x\) es 4, ¿es mayor la salida de la ecuación o la gráfica?
- ¿Para qué valor\(x\) produce la misma salida tanto en la gráfica como en la ecuación?
(De la Unidad 5.2.5)
Ejercicio\(\PageIndex{7}\)
Esta gráfica muestra un viaje en un sendero para bicicletas. El sendero tiene marcadores cada 0.5 km que muestran la distancia desde el inicio del sendero.
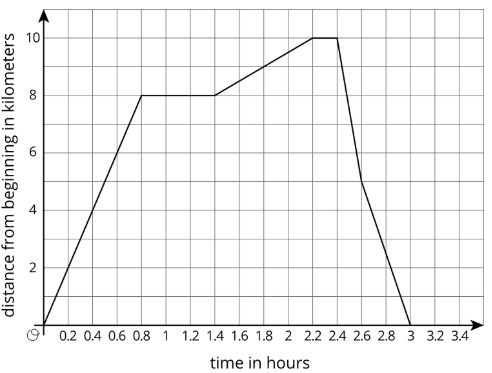
- ¿Cuándo iba el ciclista más rápido?
- ¿Cuándo iba el ciclista más lento?
- ¿Durante qué tiempos se alejaba el jinete del inicio del sendero?
- ¿Durante qué tiempos retrocedía el jinete hacia el inicio del sendero?
- ¿Durante qué horarios se detuvo el jinete?
Ejercicio\(\PageIndex{8}\)
La expresión\(-25t+1250\) representa el volumen de líquido de un recipiente después de\(t\) segundos. La expresión\(50t+250\) representa el volumen de líquido de otro recipiente después de\(t\) segundos. ¿Qué\(-25t+1250=50t+250\) significa la ecuación en esta situación?
(De la Unidad 4.2.8)