5.4.1: Llenado de Contenedores
- Page ID
- 118635
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Llenemos los recipientes con agua.
Ejercicio\(\PageIndex{1}\): Which One Doesn't Belong: Solids
Se trata de dibujos de objetos tridimensionales. ¿Cuál no pertenece? Explica tu razonamiento.
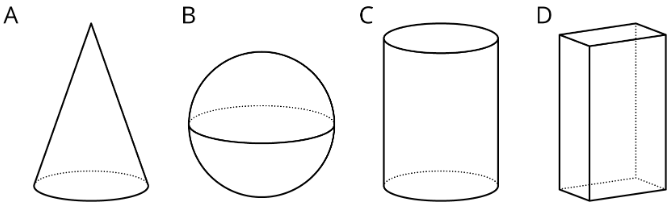
Ejercicio\(\PageIndex{2}\): Height and Volume
Use el applet para investigar la altura del agua en el cilindro en función del volumen de agua.
- Antes de comenzar, haga una predicción sobre la forma de la gráfica.
- Verifique Restablecer y establezca el radio y la altura del cilindro graduado a los valores que elija.
- Deje que el cilindro se llene con diferentes cantidades de agua y registre los datos en la tabla.
- Crear una gráfica que muestre la altura del agua en el cilindro en función del volumen de agua.
- Elija un punto en la gráfica y explique su significado en el contexto de la situación.
Ejercicio\(\PageIndex{3}\): What is the Shape?
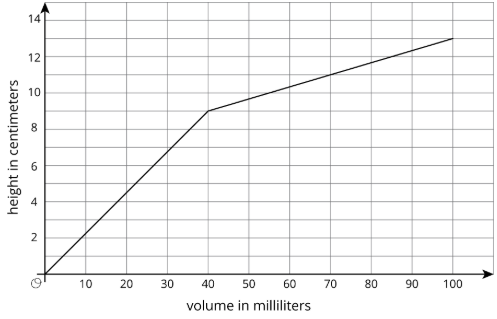
1. La gráfica muestra la función altura vs volumen de un contenedor desconocido. ¿Qué forma podría tener este contenedor? Explica cómo conoces y dibuja un posible contenedor.
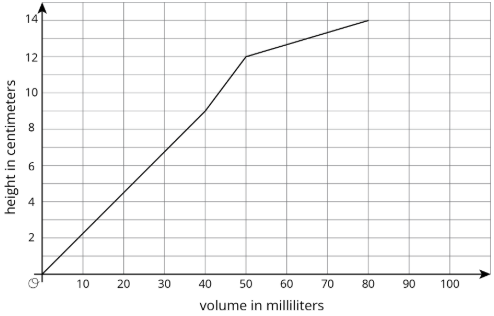
2. La gráfica muestra la función altura vs volumen de un contenedor desconocido diferente. ¿Qué forma podría tener este contenedor? Explica cómo conoces y dibuja un posible contenedor.
3. ¿En qué se parecen los dos contenedores? ¿En qué se diferencian?
¿Estás listo para más?
La gráfica muestra la función altura vs volumen de un contenedor desconocido. ¿Qué forma podría tener este contenedor? Explica cómo conoces y dibuja un posible contenedor.
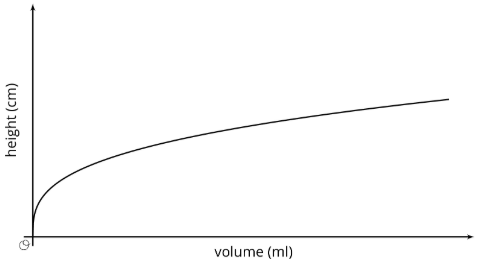
Resumen
Al llenar una forma como un cilindro con agua, podemos ver cómo las dimensiones del cilindro afectan cosas como la altura cambiante del agua. Por ejemplo, digamos que tenemos dos cilindros,\(D\) y\(E\), con la misma altura, pero\(D\) tiene un radio de 3 cm y\(E\) tiene un radio de 6 cm.
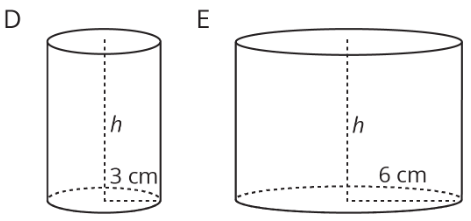
Si vertimos agua en ambos cilindros a la misma velocidad, la altura del agua en\(D\) aumentará más rápido que la altura del agua en\(E\) debido a su radio menor. Esto quiere decir que si hiciéramos gráficas de la altura del agua en función del volumen de agua para cada cilindro, tendríamos dos líneas y la pendiente de la línea para cilindro\(D\) sería mayor que la pendiente de la línea para cilindro\(E\).
Entradas en el glosario
Definición: Cylinder
Un cilindro es una figura tridimensional como un prisma, pero con bases que son círculos.
Practica
Ejercicio\(\PageIndex{4}\)
Los cilindros A, B y C tienen el mismo radio pero diferentes alturas. Poner los cilindros en orden de su volumen de menor a mayor.
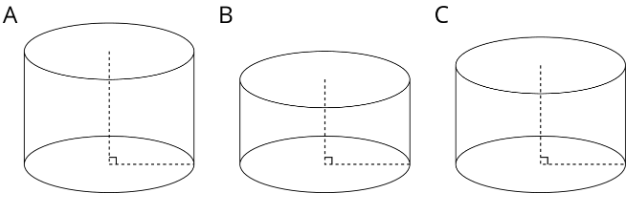
Ejercicio\(\PageIndex{5}\)
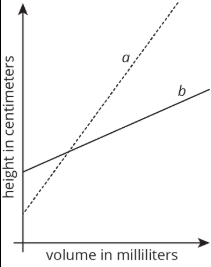
Dos cilindros,\(a\) y\(b\), cada uno comenzó con diferentes cantidades de agua. La gráfica muestra cómo la altura del agua cambió a medida que el volumen de agua aumentaba en cada cilindro. Coincidir con las gráficas de\(a\) y\(b\) con Cilindros P y Q. Explica tu razonamiento
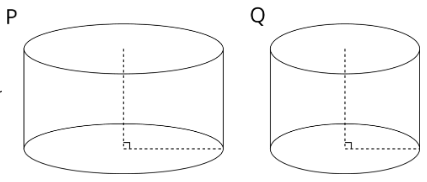
Ejercicio\(\PageIndex{6}\)
¿Cuál de las siguientes gráficas podría representar el volumen de agua en un cilindro en función de su altura? Explica tu razonamiento.
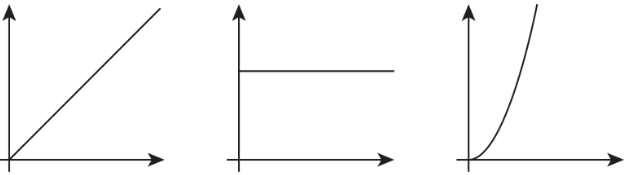
Ejercicio\(\PageIndex{7}\)
En conjunto, las áreas de los rectángulos suman 30 centímetros cuadrados.
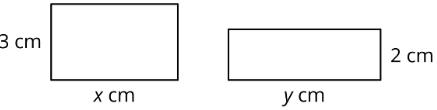
- Escribir una ecuación que muestre la relación entre\(x\) y\(y\).
- Rellene la tabla con los valores faltantes.
| \(x\) | 3 | 8 | 12 | ||
|---|---|---|---|---|---|
| \(y\) | 5 | 10 |
(De la Unidad 5.2.1)