5.4.6: Encontrar las dimensiones del cono

Última actualización
Guardar como PDF

Page ID: 118623

Illustrative Mathematics
OpenUp Resources

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lección

Averiguemos las dimensiones de los conos.

Ejercicio\(\PageIndex{1}\): Number Talk: Thirds

Para cada ecuación, decidir qué valor, en su caso, la haría cierta.

\(27=\frac{1}{3}h\)

\(27=\frac{1}{3}r^{2}\)

\(12\pi =\frac{1}{3}\pi a\)

\(12\pi =\frac{1}{3}\pi b^{2}\)

Ejercicio\(\PageIndex{2}\): An Unknown Radius

El volumen\(V\) de un cono con radio\(r\) viene dado por la fórmula\(V=\frac{1}{3}\pi r^{2}h\).

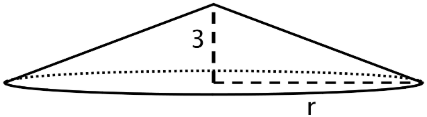
El volumen de este cono con altura 3 unidades y radio\(r\) es de unidades\(V=64\pi\) cúbicas. Esta afirmación es cierta:

\(64\pi =\frac{1}{3}\pi r^{2}\cdot 3\)

¿Cuál tiene que ser el radio de este cono? Explique cómo sabe.

Ejercicio\(\PageIndex{3}\): Cones with Unknown Dimensions

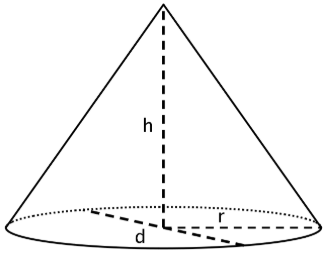
Cada fila de la tabla tiene alguna información sobre un cono en particular. Completa la mesa con las dimensiones faltantes.

Mesa\(\PageIndex{1}\)
diámetro (unidades)	radio (unidades)	área de la base (unidades cuadradas)	altura (unidades)	volumen de cono (unidades cúbicas)
	\(4\)		\(3\)
	\(\frac{1}{3}\)		\(6\)
		\(36\pi\)	\(\frac{1}{4}\)
\(20\)				\(200\pi\)
			\(12\)	\(64\pi \)
			\(3\)	\(3.14\)

¿Estás listo para más?

Un frustum es el resultado de tomar un cono y cortar un cono más pequeño usando un corte paralelo a la base.

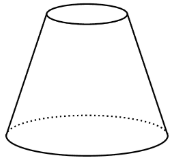
Encuentra una fórmula para el volumen de un frustum, incluyendo decidir qué cantidades vas a incluir en tu fórmula.

Ejercicio\(\PageIndex{4}\): Popcorn Deals

Una sala de cine ofrece dos contenedores:

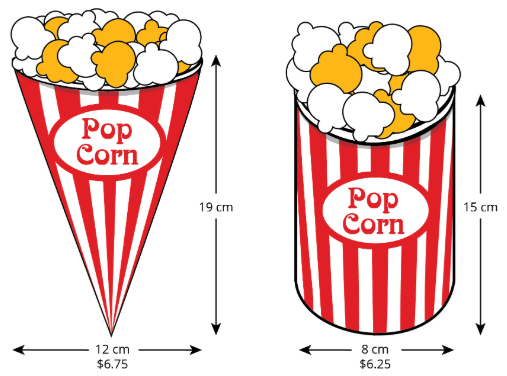
¿Qué contenedor es el mejor valor? Utilice 3.14 como aproximación para\(\pi\).

Resumen

Como vimos con los cilindros, el volumen\(V\) de un cono depende del radio\(r\) de la base y la altura\(h\):

\(V=\frac{1}{3}\pi r^{2}h\)

Si conocemos el radio y la altura, podemos encontrar el volumen. Si conocemos el volumen y una de las dimensiones (ya sea radio o altura), podemos encontrar la otra dimensión.

Por ejemplo, imagina un cono con un volumen de\(64\pi\) cm ³, una altura de 3 cm, y un radio desconocido\(r\). Por la fórmula de volumen, sabemos que

\(64\pi =\frac{1}{3}\pi r^{2}\cdot 3\)

Mirando la estructura de la ecuación, podemos ver eso\(r^{2}=64\), por lo que el radio debe ser de 8 cm.

Ahora imagina un cono diferente con un volumen de\(18\pi \) cm ³, un radio de 3 cm, y una altura desconocida\(h\). Usando la fórmula para el volumen del cono, sabemos que

\(18\pi =\frac{1}{3}\pi 3^{2}h\)

por lo que la altura debe ser de 6 cm. ¿Puedes ver por qué?

Entradas en el glosario

Definición: Cono

Un cono es una figura tridimensional como una pirámide, pero la base es un círculo.

Definición: Cilindro

Un cilindro es una figura tridimensional como un prisma, pero con bases que son círculos.

Definición: Esfera

Una esfera es una figura tridimensional en la que todas las secciones transversales en todas las direcciones son círculos.

Practica

Ejercicio\(\PageIndex{5}\)

El volumen de este cilindro es de unidades\(175\pi\) cúbicas.

¿Cuál es el volumen de un cono que tiene la misma área base y la misma altura?

(De la Unidad 5.4.5)

Ejercicio\(\PageIndex{6}\)

Un cono tiene un volumen de pulgadas\(12\pi\) cúbicas. Su altura es de 4 pulgadas. ¿Cuál es su radio?

Ejercicio\(\PageIndex{7}\)

Un cono tiene volumen\(3\pi\).

Si el radio del cono es 1, ¿cuál es su altura?
Si el radio del cono es 2, ¿cuál es su altura?
Si el radio del cono es 5, ¿cuál es su altura?
Si el radio del cono es\(\frac{1}{2}\), ¿cuál es su altura?
Si el radio del cono entra\(r\), entonces ¿cuál es la altura?

Ejercicio\(\PageIndex{8}\)

Tres personas están jugando cerca del agua. La persona A se para en el muelle. La persona B comienza en la parte superior de un poste y tirolesa hacia el agua, luego sale del agua. La persona C sale del agua y sube por el poste de tirolesa. Empareja a las personas con las gráficas donde el eje horizontal representa el tiempo en segundos y el eje vertical representa la altura por encima del nivel del agua en pies.

Figura\(\PageIndex{6}\): Plano coordenado, x, negativo 1 a 8 por 1, y, negativo 10 a 20 por 5. Tres líneas. La primera línea comienza en 0 coma 20, baja a 2 punto 5 coma negativa 5, horizontal a 4 coma negativa 5, luego aumenta a 3 coma 5. La segunda línea comienza en 0 coma 10 y permanece horizontal a 8 coma 10. La tercera línea comienza en 0 coma negativa 3 y aumenta a 8 coma 13.

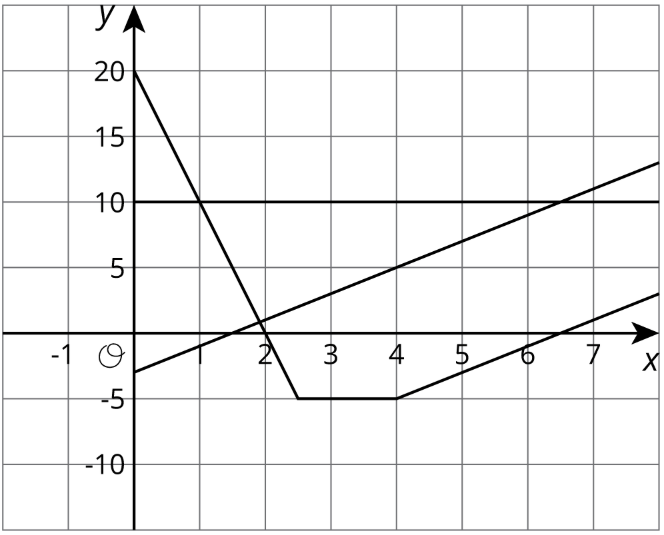
(De la Unidad 5.2.4)

Ejercicio\(\PageIndex{9}\)

Una habitación mide 15 pies de altura. Un arquitecto quiere incluir una ventana de 6 pies de altura. La distancia entre el piso y la parte inferior de la ventana es de\(b\) pies. La distancia entre el techo y la parte superior de la ventana es de\(a\) pies. Esta relación puede ser descrita por la ecuación\(a=15-(b+6)\)

¿Qué variable es independiente en función de la ecuación dada?
Si el arquitecto\(b\) quiere ser 3, ¿qué significa esto? ¿Para qué valor\(a\) trabajaría con el valor dado\(b\)?
El cliente quiere que la ventana tenga 5 pies de espacio encima de ella. ¿El cliente está describiendo\(a\) o\(b\)? ¿Cuál es el valor de la otra variable?

(De la Unidad 5.2.1)