5.5.1: Escalado de una dimensión

Lección

Veamos cómo cambiar una dimensión cambia el volumen de una forma.

Ejercicio\(\PageIndex{1}\): Driving the Distance

Aquí hay una gráfica de la cantidad de gas quemado durante un viaje por un camión tractor-remolque mientras conduce a una velocidad constante por una carretera:

Figura\(\PageIndex{1}\)

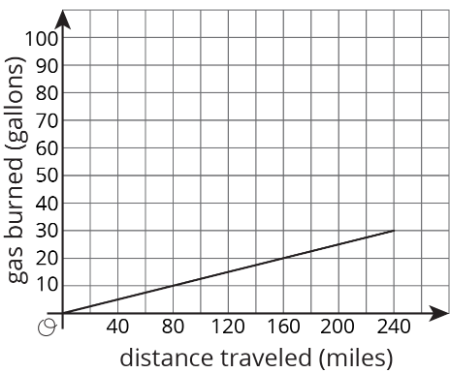
1. Al final del viaje, ¿qué tan lejos conducía la camioneta y cuánta gasolina usó?
2. Si un camión recorriera la mitad de esta distancia al mismo ritmo, ¿cuánto gas usaría?
3. Si un camión recorriera el doble de esta distancia a la misma tasa, ¿cuánto gas usaría?
4. Completa la frase: ___________ es una función de _____________.

Ejercicio\(\PageIndex{2}\): Double the Edge

Hay muchos prismas rectangulares rectos con un borde de longitud 5 unidades y otro borde de longitud 3 unidades. Dejar\(s\) representar la longitud del tercer borde y\(V\) representar el volumen de estos prismas.

1. Escribir una ecuación que represente la relación entre\(V\) y\(s\).
2. Grafica esta ecuación.
3. ¿Qué pasa con el volumen si duplicas la longitud del borde\(s\)? ¿Dónde ves esto en la gráfica? ¿Dónde lo ve algebraicamente?

Ejercicio\(\PageIndex{3}\): Halve the Height

Hay muchos cilindros con radio 5 unidades. Dejar\(h\) representar la altura y\(V\) representar el volumen de estos cilindros.

1. Escribir una ecuación que represente la relación entre\(V\) y\(h\). Usar 3.14 como aproximación de\(\pi\).
2. Grafica esta ecuación.
3. ¿Qué pasa con el volumen si se reduce a la mitad la altura,\(h\)? ¿Dónde puedes ver esto en la gráfica? ¿Cómo se puede ver algebraicamente?

¿Estás listo para más?

Supongamos que tenemos un prisma rectangular con dimensiones 2 unidades por 3 unidades por 6 unidades, y nos gustaría hacer un prisma rectangular de volumen 216 unidades cúbicas estirando una de las tres dimensiones.

• ¿Cuáles son las tres formas de hacer esto? De estos, ¿qué le da al prisma con la menor superficie?
• Repita este proceso para un prisma rectangular inicial con dimensiones 2 unidades por 6 unidades por 6 unidades.
• ¿Puedes darle algunos consejos generales a alguien que quiera hacer una caja con cierto volumen, pero quiere ahorrar costos en material al tener una superficie lo más pequeña posible?

Ejercicio\(\PageIndex{4}\): Figuring Out Cone Dimensions

Aquí hay una gráfica de la relación entre la altura y el volumen de algunos conos que tienen el mismo radio:

Figura\(\PageIndex{2}\)

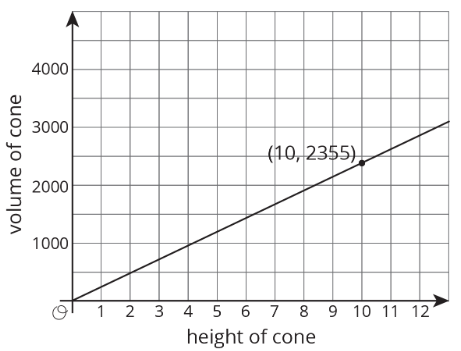
1. ¿Qué representan las coordenadas del punto etiquetado?
2. ¿Cuál es el volumen del cono con altura 5? ¿Con altura 30?
3. Utilice el punto etiquetado para encontrar el radio de estos conos. Utilice 3.14 como aproximación para\(\pi\).
4. Escribe una ecuación que relacione el volumen\(V\) y la altura\(h\).

Resumen

Imagina un cilindro con un radio de 5 cm que se está llenando de agua. A medida que aumenta la altura del agua, aumenta el volumen de agua.

Decimos que el volumen del agua en el cilindro,\(V\), depende de la altura del agua\(h\). Podemos representar esta relación con una ecuación:\(V=\pi\cdot 5^{2}h\) o simplemente

\(V=25\pi h\)

Esta ecuación representa una relación proporcional entre la altura y el volumen. Podemos usar esta ecuación para entender cómo cambia el volumen cuando se triplica la altura.

Figura\(\PageIndex{3}\)

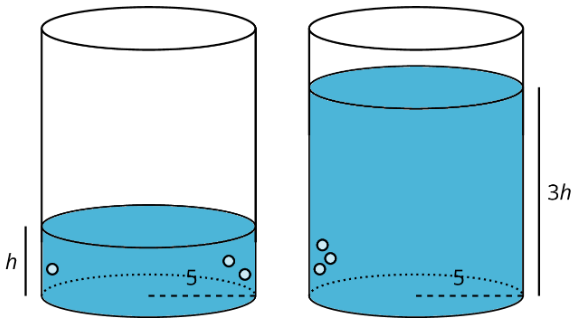
El nuevo volumen sería\(V=25\pi (3h)=75\pi h\), que es precisamente 3 veces más que el viejo volumen de\(25\pi h\). En general, cuando una cantidad en una relación proporcional cambia por un factor dado, la otra cantidad cambia por el mismo factor.

Recuerde que las relaciones proporcionales son ejemplos de relaciones lineales, que también pueden ser pensadas como funciones. Entonces en este ejemplo\(V\), el volumen de agua en el cilindro, es función de la altura\(h\) del agua.

Practica

Ejercicio\(\PageIndex{5}\)

Un cilindro tiene un volumen de\(48\pi\) cm ³ y altura\(h\). Completa esta tabla para volumen de cilindros con el mismo radio pero diferentes alturas.

Mesa\(\PageIndex{1}\)

altura (cm)	volumen (cm\(^{3}\))
\(h\)	\ (^ {3}\)) ">\(48\pi\)
\(2h\)	\ (^ {3}\)) ">
\(5h\)	\ (^ {3}\)) ">
\(\frac{h}{2}\)	\ (^ {3}\)) ">
\(\frac{h}{5}\)	\ (^ {3}\)) ">

Ejercicio\(\PageIndex{6}\)

Un cilindro tiene un radio de 3 cm y una altura de 5 cm.

1. ¿Cuál es el volumen del cilindro?
2. ¿Cuál es el volumen del cilindro cuando se triplica su altura?
3. ¿Cuál es el volumen del cilindro cuando se reduce a la mitad su altura?

Ejercicio\(\PageIndex{7}\)

Un cilindro graduado que mide 24 cm de altura puede contener 1 L de agua. ¿Cuál es el radio del cilindro? ¿Cuál es la altura de la marca de 500 ml? ¿La marca de 250 ml? Recordemos que 1 litro (L) es igual a 1000 mililitros (ml), y que 1 litro (L) es igual a 1,000 cm ³.

Ejercicio\(\PageIndex{8}\)

Una heladería ofrece dos conos de helado. El cono de gofre tiene capacidad para 12 onzas y mide 5 pulgadas de alto. El cono de azúcar también tiene capacidad para 12 onzas y mide 8 pulgadas de alto. ¿Qué cono tiene un radio mayor?

(De la Unidad 5.4.6)

Ejercicio\(\PageIndex{9}\)

Un vaso de papel de 6 oz tiene forma de cono con un diámetro de 4 pulgadas. ¿Cuántas onzas de agua aguará un vaso cilíndrico de plástico con un diámetro de 4 pulgadas si tiene la misma altura que el vaso de papel?

(De la Unidad 5.4.5)

Ejercicio\(\PageIndex{10}\)

El teléfono inteligente de Lin estaba completamente cargado cuando inició la escuela a las 8:00 a.m., a las 9:20 a.m., estaba cargado al 90%, y al mediodía, estaba cargado con 72%.

1. ¿Cuándo crees que morirá su batería?
2. ¿La duración de la batería es una función del tiempo? En caso afirmativo, ¿es una función lineal? Explica tu razonamiento.

(De la Unidad 5.3.2)