5.5.2: Escalar dos dimensiones
- Page ID
- 118606
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Cambiemos más dimensiones de formas.
Ejercicio\(\PageIndex{1}\): Tripling Statements
\(m, n, a, b\), y\(c\) todos representan enteros positivos. Considera estas dos ecuaciones:\(m=a+b+c\)\(n=abc\)
- ¿Cuáles de estas afirmaciones son ciertas? Seleccione todas las que correspondan.
- Si\(a\) se triplica,\(m\) se triplica.
- Si\(a\),\(b\), y\(c\) son todos triplicados, entonces\(m\) se triplican.
- Si\(a\) se triplica,\(n\) se triplica.
- Si\(a\),\(b\), y\(c\) son todos triplicados, entonces\(n\) se triplican.
- Crea una verdadera declaración propia sobre una de las ecuaciones.
Ejercicio\(\PageIndex{2}\): A Square Base
Clare esboza un prisma rectangular con una altura de 11 y una base cuadrada y etiqueta los bordes de la base\(s\). Ella le pregunta a Han qué piensa que le pasará al volumen del prisma rectangular si se triplica\(s\).
Han dice que el volumen será 9 veces mayor. ¿Tiene razón? Explica o muestra tu razonamiento.
¿Estás listo para más?
Se puede construir un cilindro a partir de un trozo de papel rizándolo para que puedas pegar dos bordes opuestos (los bordes punteados en la figura).
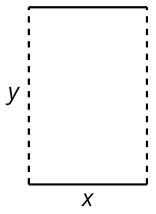
- Si quisieras aumentar el volumen dentro del cilindro resultante, ¿tendría más sentido duplicar\(x\)\(y\), o no importa?
- Si quisieras aumentar la superficie del cilindro resultante, ¿tendría más sentido duplicar\(x\)\(y\), o no importa?
- ¿Cómo cambiarían sus respuestas a estas preguntas si hiciéramos un cilindro pegando juntas las líneas continuas en lugar de las líneas discontinuas?
Ejercicio\(\PageIndex{3}\): Playing with Cones
Hay muchos conos con una altura de 7 unidades. Dejar\(r\) representar el radio y\(V\) representar el volumen de estos conos.
- Escribir una ecuación que exprese la relación entre\(V\) y\(r\). Utilice 3.14 como aproximación para\(\pi\).
- Predice qué pasa con el volumen si triples el valor de\(r\).
- Grafica esta ecuación.
- ¿Qué pasa con el volumen si triples\(r\)? ¿Dónde ves esto en la gráfica? ¿Cómo se puede ver algebraicamente?
Resumen
Hay muchos prismas rectangulares que tienen una longitud de 4 unidades y un ancho de 5 unidades pero diferentes alturas. Si\(h\) representa la altura, entonces el volumen\(V\) de dicho prisma es
\(V=20h\)
La ecuación nos muestra que el volumen de un prisma con un área base de 20 unidades cuadradas es una función lineal de la altura. Debido a que esta es una relación proporcional, si la altura se multiplica por un factor de\(a\), entonces el volumen también se multiplica por un factor de\(a\):
\(V=20(ah)\)
¿Qué pasa si escalamos dos dimensiones de un prisma por un factor de\(a\)? En este caso, el volumen se multiplica por un factor de\(a\) dos veces, o\(a^{2}\).
Por ejemplo, piense en un prisma con una longitud de 4 unidades, un ancho de 5 unidades y una altura de 6 unidades. Su volumen es de 120 unidades cúbicas desde entonces\(4\cdot 5\cdot 6=120\). Ahora imagina el largo y ancho cada uno se escala por un factor de\(a\), lo que significa que el nuevo prisma tiene una longitud de\(4a\), ancho de\(5a\), y una altura de 6. El nuevo volumen es unidades\(120a^{2}\) cúbicas desde\(4a\cdot 5a\cdot 6=120a^{2}\).
Una relación similar se mantiene para cilindros. Piense en un cilindro con una altura de 6 y un radio de 5. El volumen serían unidades\(150\pi\) cúbicas desde entonces\(\pi\cdot 5^{2}\cdot 6=150\pi \). Ahora, imagina que el radio se escala por un factor de\(a\). Entonces el nuevo volumen es\(\pi\cdot (5a)^{2}\cdot 6=\pi\cdot 25a^{2}\cdot 6\) o unidades\(150a^{2}\pi\) cúbicas. Entonces escalar el radio por un factor de\(a\) tiene el efecto de multiplicar el volumen por\(a^{2}\)!
¿Por qué el volumen se multiplica por\(a^{2}\) cuando solo cambia el radio? Esto tiene sentido si imaginamos cómo escalar el radio cambia el área base del cilindro. A medida que aumenta el radio, el área base se hace más grande en dos dimensiones (el círculo se ensancha y también más alto), mientras que la tercera dimensión del cilindro, la altura, permanece igual.
Practica
Ejercicio\(\PageIndex{4}\)
Hay muchos cilindros con una altura de 18 metros. Dejar\(r\) representar el radio en metros y\(V\) representar el volumen en metros cúbicos.
- Escribe una ecuación que represente\(V\) el volumen en función del radio\(r\).
- Completa esta tabla, dando tres posibles ejemplos.
\(r\) \(V\) \ (r\) ">1 \ (V\) "> \ (r\) "> \ (V\) "> \ (r\) "> \ (V\) "> Mesa\(\PageIndex{1}\) - Si se duplica el radio de un cilindro, ¿se duplica el volumen? Explique cómo sabe.
- ¿La gráfica de esta función es una línea? Explique cómo sabe.
Ejercicio\(\PageIndex{5}\)
Como parte de una competencia, Diego debe dar vueltas en círculo 6 veces y luego correr hacia un árbol. El tiempo que pasa en cada giro está representado por\(s\) y el tiempo que pasa corriendo lo es\(r\). Llega al árbol 21 segundos después de que empieza a girar.
- Escribir una ecuación que muestre la relación entre\(s\) y\(r\).
- Reorganizar la ecuación para que\(r\) se muestre en función de\(s\).
- Si Diego tarda 1.2 segundos en dar vueltas cada vez, ¿cuántos segundos pasó corriendo?
(De la Unidad 5.2.1)
Ejercicio\(\PageIndex{6}\)
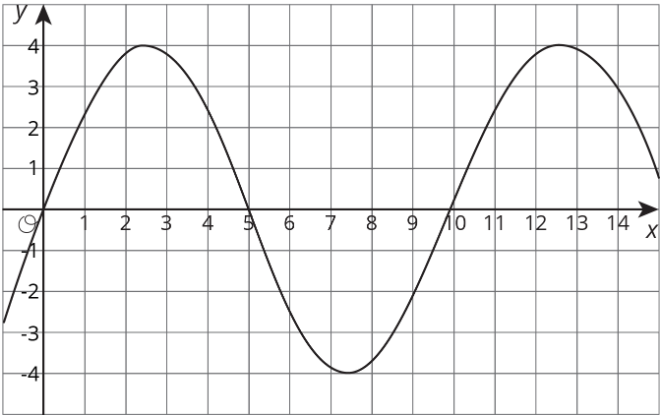
La tabla y la gráfica representan dos funciones. Utilice la tabla y la gráfica para responder a las preguntas.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| \(y\) | 3 | -1 | 0 | 4 | 5 | -1 |
- ¿Para qué valores de la salida de la tabla\(x\) es menor que la salida de la gráfica?
- En la función graficada, ¿qué valores de\(x\) dan una salida de 0?
(De la Unidad 5.2.5)
Ejercicio\(\PageIndex{7}\)
Un cono tiene un radio de 3 unidades y una altura de 4 unidades.
- ¿Qué es este volumen de este cono?
- Otro cono tiene cuadruplicado el radio, y la misma altura. ¿Cuántas veces más grande es el volumen del nuevo cono?