Saltar al contenido principal
LibreTexts Español

5.5.5: Cilindros, Conos y Esferas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118601

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Encontremos el volumen de las formas.

    Ejercicio\(\PageIndex{1}\): Sphere Adjustments

    Cuatro estudiantes calcularon cada uno el volumen de una esfera con un radio de 9 centímetros y obtuvieron cuatro respuestas diferentes.

    • Han piensa que son 108 centímetros cúbicos.
    • Jada obtuvo centímetros\(108\pi\) cúbicos.
    • Tyler calculó 972 centímetros cúbicos.
    • Mai dice que son centímetros\(972\pi\) cúbicos.

    ¿Estás de acuerdo con alguno de ellos? Explica tu razonamiento.

    Ejercicio\(\PageIndex{2}\): Sphere's Radius

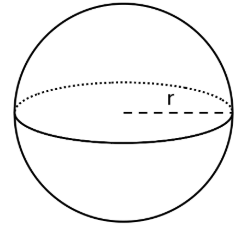
    clipboard_e2c1f7a9d4cd5a139fbf277cfccbbccdc.png
    Figura\(\PageIndex{1}\)

    El volumen de esta esfera con radio\(r\) es\(V=288\pi\). Esta afirmación es cierta:

    \(288\pi =\frac{4}{3}r^{3}\pi\). ¿Cuál es el valor de\(r\) para esta esfera? Explique cómo sabe.

    Ejercicio\(\PageIndex{3}\): Info Gap: Unknown Dimensions

    Tu profesor te dará ya sea una tarjeta de problema o una tarjeta de datos. No muestres ni leas tu tarjeta a tu pareja.

    Si tu profesor te da la tarjeta de problemas:

    1. Lee silenciosamente tu tarjeta y piensa en qué información necesitas para poder responder a la pregunta.
    2. Pídele a tu pareja la información específica que necesites.
    3. Explique cómo está utilizando la información para resolver el problema.
      Continúa haciendo preguntas hasta que tengas la información suficiente para resolver el problema.
    4. Comparte la tarjeta de problemas y resuelve el problema de forma independiente.
    5. Lee la tarjeta de datos y discute tu razonamiento.

    Si tu profesor te da la tarjeta de datos:

    1. Lee silenciosamente tu tarjeta.
    2. Pregúntale a tu pareja “¿Qué información específica necesitas?” y esperar a que pidan información.
      Si tu pareja solicita información que no esté en la tarjeta, no hagas los cálculos por ellos. Diles que no tienes esa información.
    3. Antes de compartir la información, pregunta “¿Por qué necesitas esa información? ” Escucha el razonamiento de tu pareja y haz preguntas aclaratorias.
    4. Lea la tarjeta del problema y resuelva el problema de forma independiente.
    5. Comparte la tarjeta de datos y discute tu razonamiento.

    Haz una pausa aquí para que tu profesor pueda revisar tu trabajo. Pídele a tu profesor un nuevo juego de cartas y repite la actividad, negociando roles con tu pareja.

    Ejercicio\(\PageIndex{4}\): The Right Fit

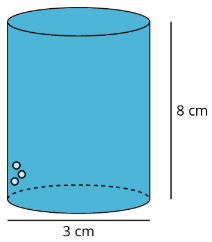
    clipboard_e065920d37064cae4822a65ec89405d69.png
    Figura\(\PageIndex{2}\)

    Un cilindro con diámetro 3 centímetros y altura 8 centímetros se llena de agua. Decidir qué cifras aquí descritas, si las hubiera, podrían contener toda el agua del cilindro. Explica tu razonamiento.

    1. Cono con una altura de 8 centímetros y un radio de 3 centímetros.
    2. Cilindro con un diámetro de 6 centímetros y altura de 2 centímetros.
    3. Prisma rectangular con una longitud de 3 centímetros, ancho de 4 centímetros y altura de 8 centímetros.
    4. Esfera con un radio de 2 centímetros.

    ¿Estás listo para más?

    Un cuervo sediento quiere elevar el nivel del agua en un recipiente cilíndrico para que pueda llegar al agua con su pico.

    • El contenedor tiene un diámetro de 2 pulgadas y una altura de 9 pulgadas.
    • El nivel del agua se encuentra actualmente en 6 pulgadas.
    • El cuervo puede llegar al agua si está a 1 pulgada de la parte superior del recipiente.

    Para elevar el nivel del agua, el cuervo pone guijarros esféricos en el contenedor. Si los guijarros tienen aproximadamente una\(\frac{1}{2}\) pulgada de diámetro, ¿cuál es el menor número de guijarros que el cuervo necesita caer en el contenedor para llegar al agua?

    Resumen

    La fórmula

    \(V=\frac{4}{3}\pi r^{3}\)

    da el volumen de una esfera con radio\(r\). Podemos usar la fórmula para encontrar el volumen de una esfera con un radio conocido. Por ejemplo, si el radio de una esfera es de 6 unidades, entonces el volumen sería

    \(\frac{4}{3}\pi (6)^{3}=288\pi\)

    o aproximadamente unidades\(904\) cúbicas. También podemos usar la fórmula para encontrar el radio de una esfera si solo conocemos su volumen. Por ejemplo, si sabemos que el volumen de una esfera son unidades\(36\pi\) cúbicas pero no conocemos el radio, entonces esta ecuación es verdadera:

    \(36\pi = \frac{4}{3}\pi r^{3}\)

    Eso significa que\(r^{3}=27\), por lo que el radio\(r\) tiene que ser de 3 unidades para que ambos lados de la ecuación tengan el mismo valor.

    Muchos objetos comunes, desde botellas de agua hasta edificios y globos, son similares en forma a prismas rectangulares, cilindros, conos y esferas, ¡o incluso combinaciones de estas formas! El uso de las fórmulas de volumen para estas formas nos permite comparar el volumen de diferentes tipos de objetos, a veces con resultados sorprendentes.

    Por ejemplo, una caja en forma de cubo con longitud lateral de 3 centímetros sostiene menos que una esfera con radio de 2 centímetros debido a que el volumen del cubo es de 27 centímetros cúbicos (\(3^{3}=27\)), y el volumen de la esfera es de alrededor de 33.51 centímetros cúbicos (\(\frac{4}{3}\pi\cdot 2^{3}\approx 33.51\)).

    Practica

    Ejercicio\(\PageIndex{5}\)

    Una cucharada de helado tiene un diámetro de 3 pulgadas. ¿Qué tan alto debe ser el cono de helado del mismo diámetro para contener todo el helado dentro del cono?

    Ejercicio\(\PageIndex{6}\)

    Calcular el volumen de las siguientes formas con la información dada. Para las tres primeras preguntas, dar cada respuesta tanto en términos de\(\pi\) como utilizando\(3.14\) para aproximar\(\pi\). Asegúrese de incluir unidades.

    1. Esfera con un diámetro de 6 pulgadas
    2. Cilindro con una altura de 6 pulgadas y un diámetro de 6 pulgadas
    3. Cono con una altura de 6 pulgadas y un radio de 3 pulgadas
    4. ¿Cómo se relacionan estos tres volúmenes?

    Ejercicio\(\PageIndex{7}\)

    Un dispensador de bolas hinchables que funciona con monedas tiene una gran esfera de vidrio que contiene muchas bolas esféricas. La gran esfera de vidrio tiene un radio de 9 pulgadas. Cada bola hinchable tiene un radio de 1 pulgada y se asienta dentro del dispensador.

    Si hay 243 bolas hinchables en la esfera de vidrio grande, ¿qué proporción del volumen de la esfera de vidrio grande ocupa las bolas hinchables? Explique cómo sabe.

    Ejercicio\(\PageIndex{8}\)

    Un agricultor tiene un tanque de agua para vacas en forma de cilindro con radio de 7 pies y una altura de 3 pies. El tanque viene equipado con un sensor para alertar al agricultor para que lo llene cuando el agua caiga al 20% de su capacidad. ¿Cuál es el volumen del tanque cuando se enciende el sensor?

    (De la Unidad 5.4.3)

    This page titled 5.5.5: Cilindros, Conos y Esferas is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.