5.6.1: Volumen en función de...
- Page ID
- 118592
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Lección
Comparemos las alturas del agua en diferentes contenedores.
Ejercicio\(\PageIndex{1}\): Missing Information
Un cilindro y una esfera tienen la misma altura.
- Si la esfera tiene un volumen de unidades\(36\pi\) cúbicas, ¿cuál es la altura del cilindro?
- ¿Cuál es un volumen posible para el cilindro? Esté preparado para explicar su razonamiento.
Ejercicio\(\PageIndex{2}\): Scaling Volume of a Sphere
- Rellene los volúmenes faltantes en términos de\(\pi\). Agrega dos pares de radio y volumen más de tu elección.
radio \(1\) \(2\) \(3\) \(\frac{1}{2}\) \(\frac{1}{3}\) \(100\) \(r\) volumen \(\frac{4}{3}\pi\) Mesa\(\PageIndex{1}\) - ¿Cómo se compara el volumen de una esfera con radio de 2 cm con el volumen de una esfera con radio de 1 cm?
- ¿Cómo se compara el volumen de una esfera con radio\(\frac{1}{2}\) cm con el volumen de una esfera con radio de 1 cm?
- Una esfera tiene un radio de longitud\(r\).
- ¿Qué pasa con el volumen de esta esfera si se duplica su radio?
- ¿Qué pasa con el volumen de esta esfera si su radio se reduce a la mitad?
- La Esfera Q tiene un volumen de 500 cm 3. La Esfera S tiene un radio\(\frac{1}{5}\) tan grande como la Esfera Q. ¿Cuál es el volumen de la Esfera S?
Ejercicio\(\PageIndex{3}\): A Cylinder, a Cone, and a Sphere
Tres recipientes de la misma altura se llenaron con agua a la misma velocidad. Un contenedor es un cilindro, uno es un cono y el otro es una esfera. A medida que se llenaban, la relación entre el volumen de agua y la altura del agua se registró de diferentes maneras, que se muestran aquí:
- Cilindro:\(h=\frac{V}{4\pi}\)
- Cono:
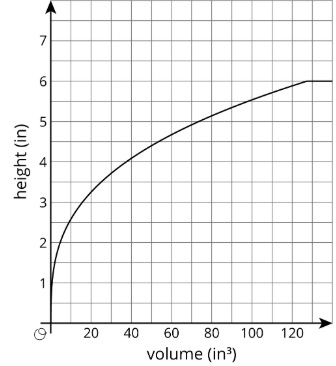
- Esfera:
| volumen (pulg\(^{3}\)) | altura (pulg) |
|---|---|
| \ (^ {3}\)) ">0 | 0 |
| \ (^ {3}\)) ">8.38 | 1 |
| \ (^ {3}\)) ">29.32 | 2 |
| \ (^ {3}\)) ">56.55 | 3 |
| \ (^ {3}\)) ">83.76 | 4 |
| \ (^ {3}\)) ">104.72 | 5 |
| \ (^ {3}\)) ">113.04 | 6 |
| \ (^ {3}\)) ">120 | 6 |
| \ (^ {3}\)) ">200 | 6 |
- El volumen máximo de agua que puede contener el cilindro es\(24\pi\). ¿Cuál es el radio del cilindro?
- Grafique la relación entre el volumen de agua vertida en el cilindro y la altura del agua en el cilindro en los mismos ejes que el cono. ¿Qué representa la pendiente de esta línea?
- ¿Qué contenedor puede caber el mayor volumen de agua? ¿El más pequeño?
- ¿Sobre cuánta agua se necesita para que el cilindro y la esfera tengan la misma altura? ¿El cilindro y el cono? Explica cómo sabes.
- ¿Para qué rango aproximado de volúmenes es mayor la altura del agua en el cilindro que la altura del agua en el cono? Explica cómo sabes.
- ¿Para qué rango aproximado de volúmenes es menor la altura del agua en la esfera que la altura del agua en el cilindro? Explica cómo sabes.