6.3.1: Buscando Asociaciones
- Page ID
- 118742
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Busquemos asociaciones en los datos.
Ejercicio\(\PageIndex{1}\): Notice and Wonder: Bar Association
¿Qué notas? ¿Qué te preguntas?
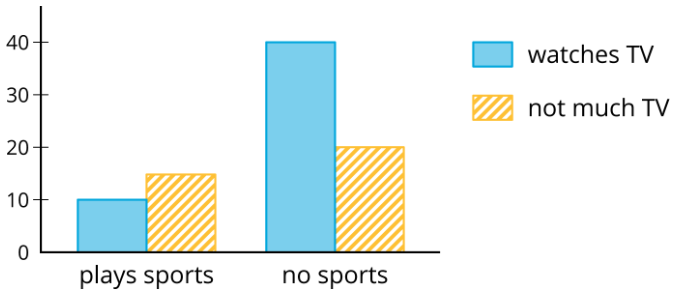
Ejercicio\(\PageIndex{2}\): Card Sort: Matching Representations
Tu profesor repartirá algunas tarjetas.
Algunas tarjetas muestran mesas bidireccionales como esta:
| cuenta con celular | no tiene celular | total | |
|---|---|---|---|
| De 10 a 12 años | 25 | 35 | 60 |
| De 13 a 15 años | 40 | 10 | 50 |
| 16 a 18 años | 50 | 10 | 60 |
| total | 115 | 55 | 170 |
Algunas tarjetas muestran gráficos de barras como este:
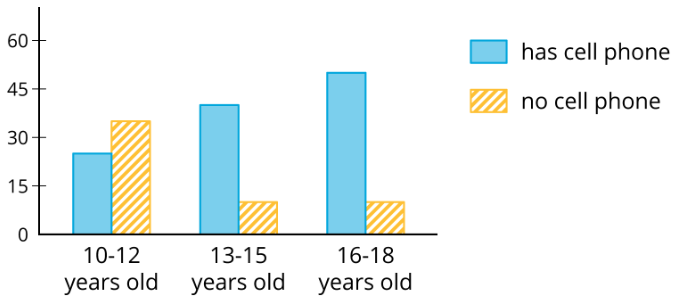
Algunas tarjetas muestran gráficas de barras segmentadas como esta:
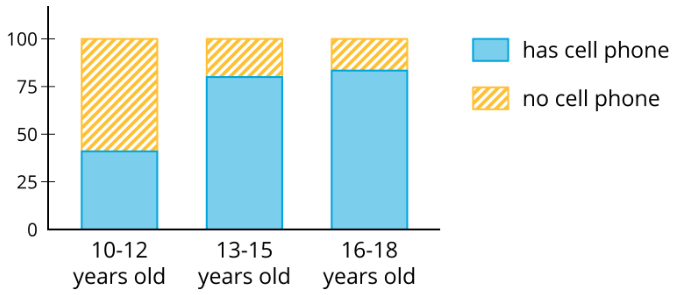
Las gráficas de barras y las gráficas de barras segmentadas tienen sus etiquetas eliminadas.
- Poner en un mismo grupo todas las tarjetas que describan la misma situación.
- Uno de los grupos no tiene una mesa de dos vías. Hacer una tabla bidireccional para la situación descrita por las gráficas del grupo.
- Etiquete los gráficos de barras y los gráficos de barras segmentados para que se indiquen las categorías representadas por cada barra.
- Describa con sus propias palabras el tipo de información que muestra un gráfico de barras segmentado.
¿Estás listo para más?
Falta uno de los gráficos de barras segmentados. Construye un gráfico de barras segmentado que coincida con las otras representaciones.
Ejercicio\(\PageIndex{3}\): Building Another Type of Two-Way Table
Aquí hay una tabla bidireccional que muestra datos sobre el uso del teléfono celular entre niños de 10 a 18 años.
| cuenta con celular | no tiene celular | total | |
|---|---|---|---|
| De 10 a 12 años | 25 | 35 | 60 |
| De 13 a 15 años | 40 | 10 | 50 |
| 16 a 18 años | 50 | 10 | 60 |
| total | 115 | 55 | 170 |
1. Completa la tabla. En cada fila, las entradas para “tiene celular” y “no tiene celular” deben tener el total del 100%. Redondear las entradas al punto porcentual más cercano.
| cuenta con celular | no tiene celular | total | |
|---|---|---|---|
| De 10 a 12 años | 42% | ||
| De 13 a 15 años | 100% | ||
| 16 a 18 años | 17% |
Esta sigue siendo una mesa de dos vías. En lugar de mostrar la frecuencia, esta tabla muestra la frecuencia relativa.
2. Las tablas bidireccionales que muestran frecuencias relativas a menudo no incluyen una fila “total” en la parte inferior. ¿Por qué?
3. ¿Existe una asociación entre la edad y el uso del celular? ¿Cómo ayuda a ilustrar esto la tabla bidireccional de frecuencias relativas?
¿Estás listo para más?
Un encuestador asiste a un mitin y encuesta a muchos de los participantes sobre si se asocian con el Partido político A o al Partido político B y si están a favor o en contra de la Proposición 3.14 subiendo pronto a votación. Los resultados se ordenan en la tabla que se muestra.
| para | contra | |
|---|---|---|
| fiesta A | 832 | 165 |
| partido B | 80 | 160 |
- Un noticiero reporta estos resultados diciendo: “Una encuesta muestra que aproximadamente el mismo número de personas de ambos partidos están votando en contra de la Proposición 3.14”.
- Una segunda estación de noticias muestra este gráfico.
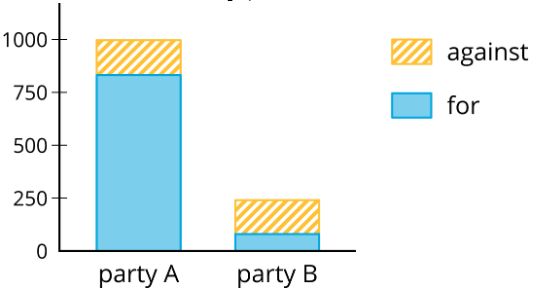
- ¿Alguno de los reportes noticiosos es engañoso? Explica tu razonamiento.
- Cree un titular, un gráfico y una breve descripción que represente con mayor precisión los datos de la tabla.
Resumen
Cuando recolectamos datos contando cosas en varias categorías, como rojo, azul o amarillo, llamamos a los datos datos categóricos, y decimos que el color es una variable categórica.
Podemos usar tablas bidireccionales para investigar posibles conexiones entre dos variables categóricas. Por ejemplo, esta tabla bidireccional de frecuencias muestra los resultados de un estudio de meditación y estado mental de los atletas antes de un encuentro de pista.
| meditó | no meditó | total | |
|---|---|---|---|
| calma | 45 | 8 | 53 |
| agitado | 23 | 21 | 44 |
| total | 68 | 29 | 97 |
Si nos interesa la cuestión de si existe una asociación entre meditar y estar tranquilo, podríamos presentar las frecuencias en un gráfico de barras, agrupando datos sobre meditadores y agrupando datos sobre no meditadores, para poder comparar los números de atletas tranquilos y agitados en cada grupo.
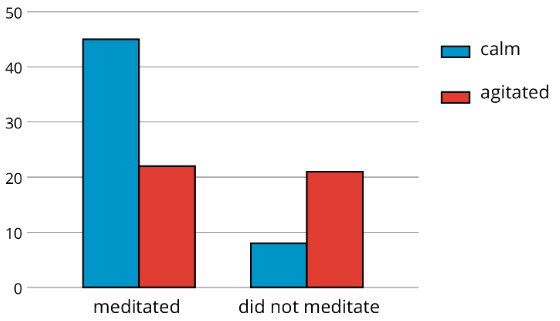
Observe que el número de atletas que no meditaron es pequeño en comparación con el número que meditó (29 en comparación con 68, como se muestra en la tabla).
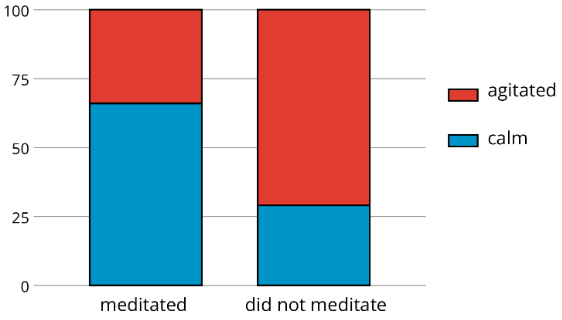
Si queremos conocer las proporciones de meditadores tranquilos y no meditadores tranquilos, podemos hacer una tabla bidireccional de frecuencias relativas y presentar las frecuencias relativas en un gráfico de barras segmentado.
| meditó | no meditó | |
|---|---|---|
| calma | 66% | 28% |
| agitado | 34% | 72% |
| total | 100% | 100% |
Entradas en el glosario
Definición: Frecuencia relativa
La frecuencia relativa de una categoría nos indica la proporción en la que se produce la categoría en el conjunto de datos. Se expresa como una fracción, un decimal o un porcentaje del número total.
Por ejemplo, supongamos que había 21 perros en el parque, algunos blancos, algunos marrones, algunos negros y algunos multicolores. La tabla muestra la frecuencia y la frecuencia relativa de cada color.
| color | frecuencia | frecuencia relativa |
|---|---|---|
| blanco | \(5\) | \(\frac{5}{21}\) |
| marrón | \(7\) | \(\frac{7}{21}\) |
| negro | \(3\) | \(\frac{3}{21}\) |
| Multicolor | \(6\) | \(\frac{6}{21}\) |
Definición: Gráfico de barras segmentado
Un gráfico de barras segmentado compara dos categorías dentro de un conjunto de datos. Toda la barra representa todos los datos dentro de una categoría. Después, cada barra se separa en partes (segmentos) que muestran el porcentaje de cada parte en la segunda categoría.
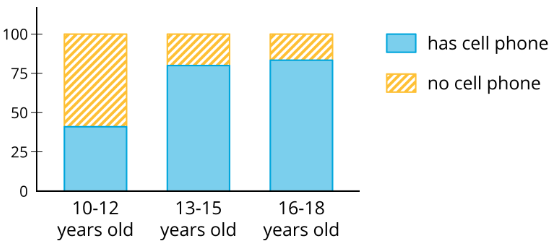
Este gráfico de barras segmentado muestra el porcentaje de personas en diferentes grupos de edad que tienen y no tienen celular. Por ejemplo, entre las personas de 10 a 12 años, alrededor del 40% tiene un celular y el 60% no tiene un celular.
Definición: Mesa de dos vías
Una tabla bidireccional proporciona una manera de comparar dos variables categóricas.
Muestra una de las variables en la parte superior y la otra hacia abajo por un lado. Cada entrada en la tabla es la frecuencia o frecuencia relativa de la categoría mostrada por los encabezamientos de columna y fila.
Un estudio investiga la conexión entre la meditación y el estado de ánimo de los atletas antes de un encuentro de pista. Esta tabla bidireccional muestra los resultados del estudio.
| meditó | no meditó | total | |
|---|---|---|---|
| calma | 45 | 8 | 53 |
| agitado | 23 | 21 | 44 |
| total | 68 | 29 | 97 |
Practica
Ejercicio\(\PageIndex{4}\)
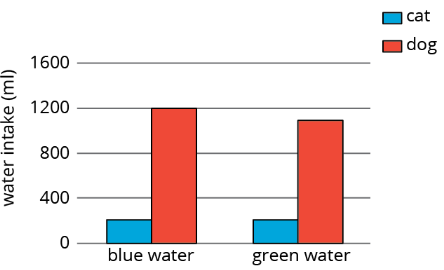
Un científico quiere saber si el color del agua afecta la cantidad de animales que beben. La cantidad promedio de agua que bebe cada animal se registró en mililitros durante una semana y luego se graficó. ¿Hay evidencia que sugiera una asociación entre el color del agua y el animal?
| ingesta de gatos (mL) | ingesta de perros (mL) | total (mL) | |
|---|---|---|---|
| agua azul | 210 | 1200 | 1410 |
| agua verde | 200 | 1100 | 1300 |
| total | 410 | 2300 | 2710 |
Ejercicio\(\PageIndex{5}\)
Un agricultor lleva sus productos al mercado del granjero y registra si la gente compra lechuga, manzanas, ambos, o algo más.
| manzanas compradas | no compré manzanas | |
|---|---|---|
| lechuga comprada | 14 | 58 |
| no compré lechuga | 8 | 29 |
Hacer una tabla que muestre las frecuencias relativas para cada fila. Usa esta tabla para decidir si existe una asociación entre comprar lechuga y comprar manzanas.
Ejercicio\(\PageIndex{6}\)
Investigadores de una compañía de medios quieren estudiar hábitos de lectura de noticias entre diferentes grupos de edad. Hicieron un seguimiento de los datos impresos y de suscripción en línea e hicieron una tabla bidireccional.
| medios de internet | medios impresos | |
|---|---|---|
| 18-25 años | 151 | 28 |
| 26-45 años | 132 | 72 |
| 46-65 años | 48 | 165 |
- Cree un gráfico de barras segmentado usando una barra por cada fila de la tabla.
- ¿Existe una asociación entre los grupos de edad y el método que utilizan para leer artículos? Explica tu razonamiento.
Ejercicio\(\PageIndex{7}\)
Usando los datos en el diagrama de dispersión, ¿cuál es una pendiente razonable de un modelo que se ajuste a estos datos?
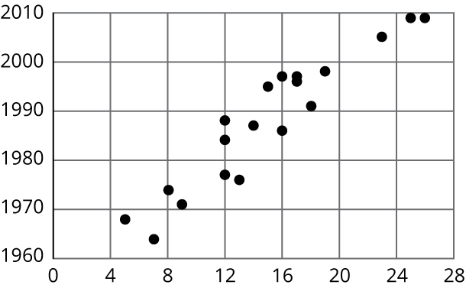
- \(-2.5\)
- \(-1\)
- \(1\)
- \(2.5\)
(De la Unidad 6.2.4)