6.3.2: Uso de pantallas de datos para encontrar asociaciones

Última actualización
Guardar como PDF

Page ID: 118741

Illustrative Mathematics
OpenUp Resources

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lección

Usemos pantallas de datos para encontrar asociaciones.

Ejercicio\(\PageIndex{1}\): Sports and Musical Instruments

Para una encuesta, los alumnos de una clase respondieron estas preguntas:

¿Practicas un deporte?
¿Tocas un instrumento musical?

1. Aquí hay una tabla bidireccional que da algunos resultados de la encuesta. Completar la tabla, asumiendo que todos los alumnos contestaron ambas preguntas.

Mesa\(\PageIndex{1}\)
	toca instrumento	no toca el instrumento	total
juega deporte	5		16
no practica deporte
total		15	25

2. Al punto porcentual más cercano, ¿qué porcentaje de alumnos que practican un deporte no tocan un instrumento musical?

3. Al punto porcentual más cercano, ¿qué porcentaje de alumnos que no practican un deporte tampoco tocan un instrumento musical?

Ejercicio\(\PageIndex{2}\): Sports and Music Association

Tu profesor te dará una mesa bidireccional con información sobre el número de personas en tu clase que tocan instrumentos deportivos o musicales.

1. Complete esta tabla para hacer una tabla bidireccional para los datos anteriores. La tabla mostrará las frecuencias relativas por fila.

Mesa\(\PageIndex{2}\)
	toca instrumento	no toca el instrumento	total de fila
juega deporte			100%
no practica deporte			100%

2. Hacer un gráfico de barras segmentado para la tabla. Utilice una barra de la gráfica para cada fila de la tabla.

3. Complete la tabla para hacer una tabla bidireccional para los datos anteriores. En la tabla se mostrarán las frecuencias relativas por columna.

Mesa\(\PageIndex{3}\)
	toca instrumento	no toca el instrumento
juega deporte
no practica deporte
total de la columna	100%	100%

4. Usando los valores de la tabla, haz un gráfico de barras segmentado. Utilice una barra de la gráfica para cada columna de la tabla.

5. Con base en las tablas bidireccionales y los gráficos de barras segmentados, ¿crees que existe una asociación entre practicar un deporte y tocar un instrumento musical? Explique cómo sabe.

Ejercicio\(\PageIndex{3}\): Colored Erasers

Una fábrica de goma de borrar cuenta con cinco máquinas. Una máquina hace que las formas de borrador. Entonces cada forma pasa por la máquina roja, máquina azul, máquina amarilla o máquina verde para tener un lado coloreado.

El gerente nota que un lado sin color de algunas gomas de borrar tiene fallas al final del proceso y quiere saber qué máquina necesita ser arreglada: la máquina de formas o algunas de las máquinas de color. El gerente recopiló datos sobre el número de gomas de borrar defectuosas e impecables de cada color.

Mesa\(\PageIndex{4}\)
	intacto	viciado	total
rojo	285	15	300
azul	223	17	240
amarillo	120	80	200
verde	195	65	260
total	823	177	1000

Trabajar con un compañero. Cada uno de ustedes debe hacer una gráfica de barras segmentada para los datos de la tabla. Un gráfico de barras segmentado debe tener una barra para cada fila de la tabla. El otro gráfico de barras segmentado debe tener una barra por cada columna de la tabla.
¿Los borradores defectuosos están asociados con ciertos colores? Si es así, ¿qué colores? Explica tu razonamiento.

¿Estás listo para más?

Con base en los presupuestos federales para 2009, la tabla muestra hacia dónde se esperaba que fuera parte del dinero federal. Los valores están en miles de millones de dólares estadounidenses.

Mesa\(\PageIndex{5}\)
	Estados Unidos	Japón	Reino Unido
defensa	718.4	42.8	49.2
educación	44.9	47.5	113.9

¿Por qué sería más útil un gráfico de barras segmentado que la tabla de datos para ver alguna asociación entre el país y dónde se gasta el dinero?
Cree un gráfico de barras segmentado que represente los datos de la tabla.
¿Existe una asociación entre el presupuesto del país y su gasto en estas áreas? Explica tu razonamiento.

Resumen

En una lección anterior, observamos datos sobre la meditación y el estado mental en los atletas.

Figura\(\PageIndex{3}\): Gráfica de barras dobles en azul y rojo. Horizontal etiquetada meditó y no meditó. Vertical etiquetada de 0 a 50. El azul representa la calma. El rojo representa agitado.

Figura\(\PageIndex{4}\): Gráfico de barras apiladas en azul y rojo. Horizontal etiquetada meditó y no meditó. Vertical etiquetada de 0 a 100. El azul representa la calma. El rojo representa agitado.

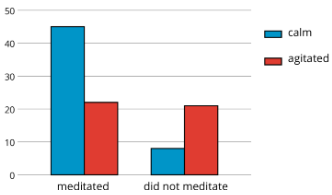
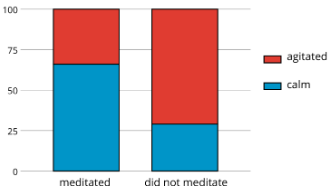
¿Existe una asociación entre la meditación y el estado de ánimo?

El gráfico de barras muestra que más atletas estaban tranquilos que agitados entre el grupo que meditó, y más atletas estaban agitados que tranquilos entre el grupo que no lo hizo. Podemos ver las proporciones de meditadores tranquilos y no meditadores tranquilos a partir del gráfico de barras segmentado, que muestra que alrededor del 66% de los atletas que meditaron estaban tranquilos, mientras que solo alrededor del 27% de los que no meditaron estaban tranquilos.

Esto no significa necesariamente que la meditación cause calma; podría ser al revés, que los atletas tranquilos estén más inclinados a meditar. Pero sí sugiere que existe una asociación entre la meditación y la calma.

Entradas en el glosario

Definición: Frecuencia relativa

La frecuencia relativa de una categoría nos indica la proporción en la que se produce la categoría en el conjunto de datos. Se expresa como una fracción, un decimal o un porcentaje del número total.

Por ejemplo, supongamos que había 21 perros en el parque, algunos blancos, algunos marrones, algunos negros y algunos multicolores. La tabla muestra la frecuencia y la frecuencia relativa de cada color.

Mesa\(\PageIndex{6}\)
color	frecuencia	frecuencia relativa
blanco	\(5\)	\(\frac{5}{21}\)
marrón	\(7\)	\(\frac{7}{21}\)
negro	\(3\)	\(\frac{3}{21}\)
Multicolor	\(6\)	\(\frac{6}{21}\)

Definición: Gráfico de barras segmentado

Un gráfico de barras segmentado compara dos categorías dentro de un conjunto de datos. Toda la barra representa todos los datos dentro de una categoría. Después, cada barra se separa en partes (segmentos) que muestran el porcentaje de cada parte en la segunda categoría.

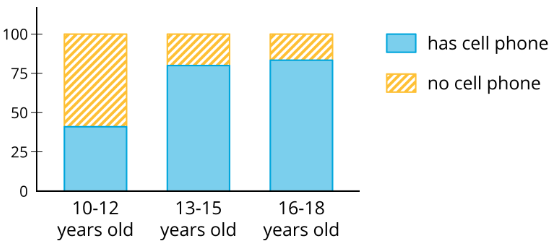
Este gráfico de barras segmentado muestra el porcentaje de personas en diferentes grupos de edad que tienen y no tienen celular. Por ejemplo, entre las personas de 10 a 12 años, alrededor del 40% tiene un celular y el 60% no tiene un celular.

Definición: Mesa de dos vías

Una tabla bidireccional proporciona una manera de comparar dos variables categóricas.

Muestra una de las variables en la parte superior y la otra hacia abajo por un lado. Cada entrada en la tabla es la frecuencia o frecuencia relativa de la categoría mostrada por los encabezamientos de columna y fila.

Un estudio investiga la conexión entre la meditación y el estado mental de los atletas antes de un encuentro de pista. Esta tabla bidireccional muestra los resultados del estudio.

Mesa\(\PageIndex{7}\)
	meditó	no meditó	total
calma	45	8	53
agitado	23	21	44
total	68	29	97

Practica

Ejercicio\(\PageIndex{4}\)

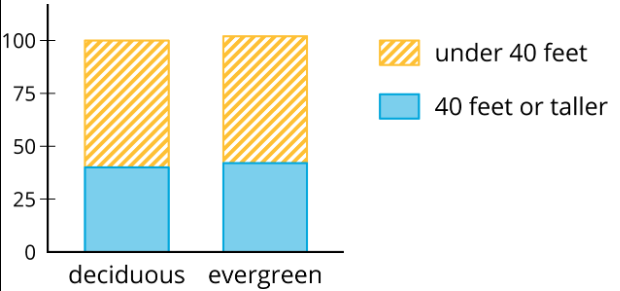
Un ecologista está estudiando un bosque con una mezcla de tipos de árboles. Dado que la altura promedio del árbol en la zona es de 40 pies, mide la altura del árbol contra eso. También registra el tipo de árbol. Los resultados se muestran en la tabla y en la gráfica de barras segmentadas. ¿Hay evidencia de asociación entre la altura del árbol y el tipo de árbol? Explica tu razonamiento.

Mesa\(\PageIndex{8}\)
	por debajo de 40 pies	40 pies o más	total
caducifolios	45	30	75
hoja perenne	14	10	24
total	59	40	99

Ejercicio\(\PageIndex{5}\)

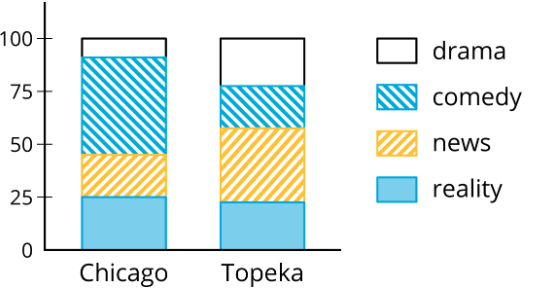
Los trabajadores de una agencia de publicidad están interesados en los hábitos de visualización de televisión de las personas. Hacen una encuesta a personas en dos ciudades para tratar de encontrar patrones en los tipos de espectáculos que ven. Los resultados se registran en una tabla y se muestran en un gráfico de barras segmentado. ¿Hay evidencia de diferentes hábitos de visualización? Si es así, explique.

Mesa\(\PageIndex{9}\)
	realidad	noticias	comedia	drama
Chicago	50	40	90	20
Topeka	45	70	40	45

Ejercicio\(\PageIndex{6}\)

A un científico le interesa saber si a ciertas especies de mariposas les gustan ciertos tipos de flores locales. El científico captura mariposas en dos zonas con diferentes tipos de flores y registra el número capturado. ¿Estos datos muestran una asociación entre el tipo de mariposa y la zona? Explica tu razonamiento.

Mesa\(\PageIndex{10}\)
	zona 1	zona 2
cola de golondrina de tigre oriental	16	34
monarca	24	46