7.3.3: Representar números pequeños en la línea numérica

Última actualización
Guardar como PDF

Page ID: 118810

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Visualicemos números pequeños en la línea numérica usando una potencia de 10.

Ejercicio$\PageIndex{1}$: Small Numbers on a Number Line

Kiran dibujó esta línea numérica.

Figura$\PageIndex{1}$: Una línea numérica, 11 marcas de verificación, 0, 1 veces 10 a la potencia negativa 4, 2 veces 10 a la potencia negativa 4, 3 veces 10 a la potencia negativa 4, 4 veces 10 a la potencia negativa 4, 5 veces 10 a la potencia negativa 4, 6 veces 10 a la potencia negativa 4, 7 veces 10 a la potencia negativa 4, 8 veces 10 a la potencia negativa 4, 9 veces 10 a la potencia negativa 4, 10 a la potencia negativa 5.

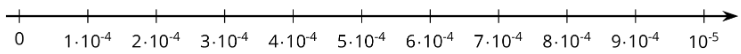
Andre dijo: “Eso no me parece correcto”.

Explica por qué Kiran tiene razón o explica cómo puede fijar la recta numérica.

Ejercicio$\PageIndex{2}$: Comparing Small Numbers on a Number Line

Etiquete las marcas de la línea numérica.
Trazar los siguientes números en la recta numérica:
1. $6\cdot 10^{-6}$
2. $6\cdot 10^{-7}$
3. $29\cdot 10^{-7}$
4. $(0.7)\cdot 10^{-5}$
¿Cuál es más grande,$29\cdot 10^{-7}$ o$6\cdot 10^{-6}$? Estimar cuántas veces más grandes.
¿Cuál es más grande,$7\cdot 10^{-8}$ o$3\cdot 10^{-9}$? Estimar cuántas veces más grandes.

Ejercicio$\PageIndex{3}$: Atomic Scale

El radio de un electrón es de aproximadamente 0.0000000000003 cm.
1. Escribe este número como múltiplo de potencia 10.
2. Decide qué poder de 10 poner en el lado derecho de esta línea numérica y etiquetarlo.
3. Etiquete cada marca de garrapata como un múltiplo de una potencia de 10.
  $clipboard_ea38eb250df7b57323548dd65eadb25aa.png$
  Figura$\PageIndex{3}$
4. Trazar el radio del electrón en centímetros en la recta numérica.
La masa de un protón es de aproximadamente 0.0000000000000000000000017 gramos.
1. Escribe este número como múltiplo de una potencia de 10.
2. Decide qué poder de 10 poner en el lado derecho de esta línea numérica y etiquetarlo.
3. Etiquete cada marca de garrapata como un múltiplo de una potencia de 10.
  $clipboard_e391e4ce1645485474347f0ede6e7bef2.png$
  Figura$\PageIndex{4}$
4. Trazar la masa del protón en gramos en la recta numérica.
El punto$A$ en la línea numérica ampliada describe la longitud de onda de una cierta radiografía en metros.

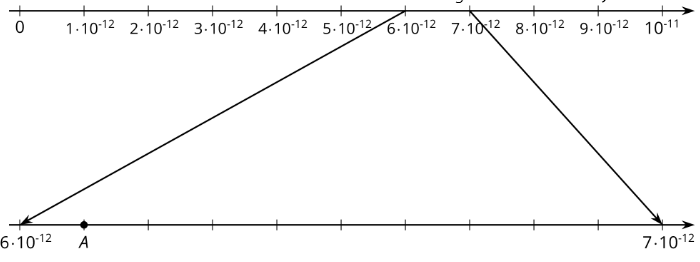
Figura$\PageIndex{5}$
1. Escriba la longitud de onda de los rayos X como una potencia múltiple de 10.
2. Escribe la longitud de onda de la radiografía como decimal.

Resumen

El ancho de una célula bacteriana es de unos$2\cdot 10^{-6}$ metros. Si queremos trazar esto en una recta numérica, necesitamos encontrar entre qué dos potencias de 10 se encuentra. Podemos ver que$2\cdot 10^{-6}$ es un múltiplo de$10^{-6}$. Entonces nuestra línea numérica será etiquetada con múltiplos de$10^{-6}$

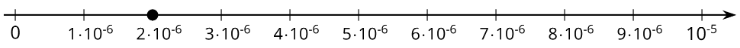
Tenga en cuenta que el lado derecho está etiquetado$10\cdot 10^{-6}=10^{-5}$

La potencia de diez en el lado derecho de la línea numérica siempre es mayor que la potencia de la izquierda. Esto es cierto para potencias con exponentes positivos o negativos.

Practica

Ejercicio$\PageIndex{4}$

Seleccione todas las expresiones que sean iguales a

$4\cdot\left(\frac{1}{10}\right)\cdot\left(\frac{1}{10}\right)\cdot\left(\frac{1}{10}\right)$
$4\cdot (-10)\cdot (-10)\cdot (-10)$
$4\cdot 0.001$
$4\cdot 0.0001$
$0.004$
$0.0004$

Ejercicio$\PageIndex{5}$

Escribe cada expresión como un múltiplo de una potencia de 10:

0.04
0.072
0.0000325
Tres milésimas
23 centésimas
729 milésimas
41 millonésimas

Ejercicio$\PageIndex{6}$

Una familia emprende un viaje por carretera para visitar a sus primos. Viajan a un ritmo constante. La gráfica muestra la distancia restante a la casa de sus primos por cada hora del viaje.

¿Qué tan rápido viajan?
¿La pendiente es positiva o negativa? Explica cómo sabes y por qué eso encaja con la situación.
¿Qué tan lejos está el viaje y cuánto tiempo tardó? Explique cómo sabe.

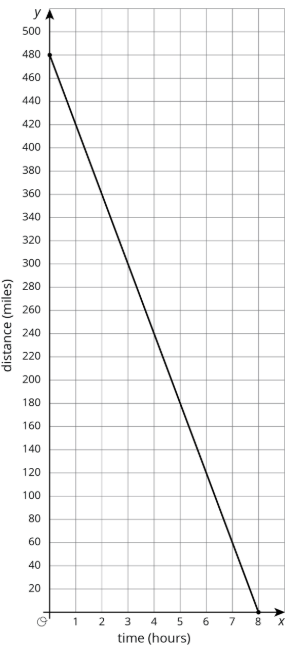
(De la Unidad 3.3.1)

Search

Text Color

Text Size

Margin Size

Font Type