Saltar al contenido principal
LibreTexts Español

8.1.1: Las áreas de los cuadrados y sus longitudes laterales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118642

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Investiguemos los cuadrados y sus longitudes laterales.

    Ejercicio\(\PageIndex{1}\): Two Regions

    ¿Qué región sombreada es más grande? Explica tu razonamiento.

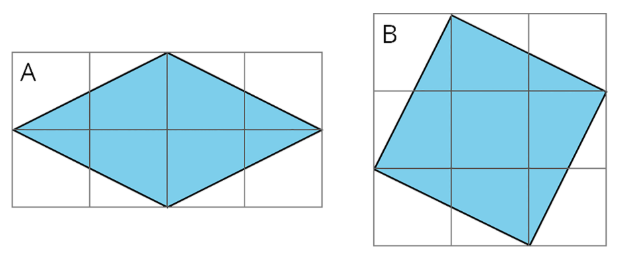
    clipboard_e807a4c3e75d3554179367531d0bcea69.png
    Figura\(\PageIndex{1}\)

    Ejercicio\(\PageIndex{2}\): Decomposing to Find Area

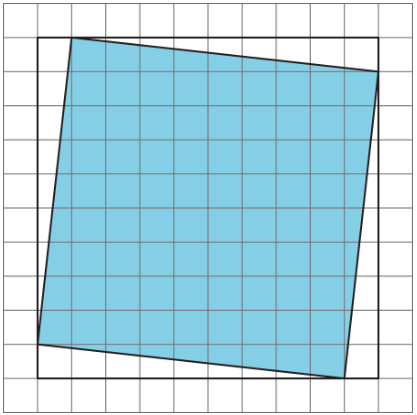
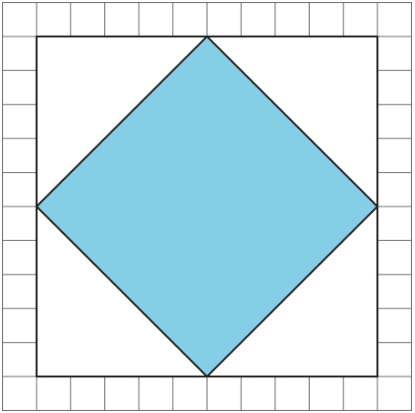
    Encuentra el área de cada cuadrado sombreado (en unidades cuadradas).

    1.

    clipboard_e47745377faccdae9d6a1e580fbb72106.png
    Figura\(\PageIndex{2}\)

    2.

    clipboard_e807ad3d25b4a869ac74b46cf4a5c69b2.png
    Figura\(\PageIndex{3}\)

    3.

    clipboard_ea0b288dfd6df614e42619c4a8cfafdd4.png
    Figura\(\PageIndex{4}\)

    ¿Estás listo para más?

    Cualquier triángulo con una base de 13 y una altura de 5 tiene un área de\(\frac{65}{2}\).

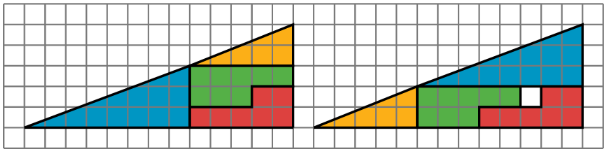
    clipboard_e55186455eb837c328e570bebf82886db.png
    Figura\(\PageIndex{5}\)

    Ambas formas en la figura se han dividido en las mismas cuatro piezas. Encuentra el área de cada una de las piezas, y verifica que las partes correspondientes sean las mismas en cada imagen. Parece haber una unidad cuadrada extra de área en la figura derecha. Si todas las piezas tienen la misma área, ¿cómo es esto posible?

    Ejercicio\(\PageIndex{3}\): Estimating Side Lengths from Areas

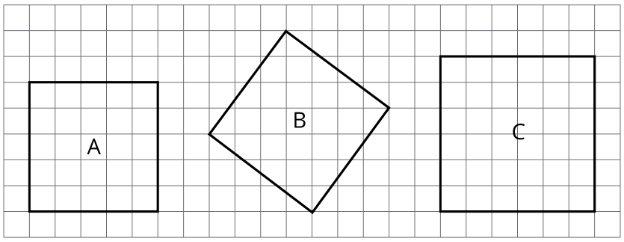
    clipboard_ec77bcfc27ec51b634e7d0c89814e6468.png
    Figura\(\PageIndex{6}\)
    1. ¿Cuál es la longitud lateral del cuadrado A? ¿Cuál es su área?
    2. ¿Cuál es la longitud lateral del cuadrado C? ¿Cuál es su área?
    3. ¿Cuál es el área del cuadrado B? ¿Cuál es su longitud lateral? (Use papel de calco para verificar su respuesta a esto).
    4. Encuentra las áreas de los cuadrados D, E y F. ¿Cuál de estos cuadrados debe tener una longitud lateral que sea mayor que 5 pero menor que 6? Explique cómo sabe.
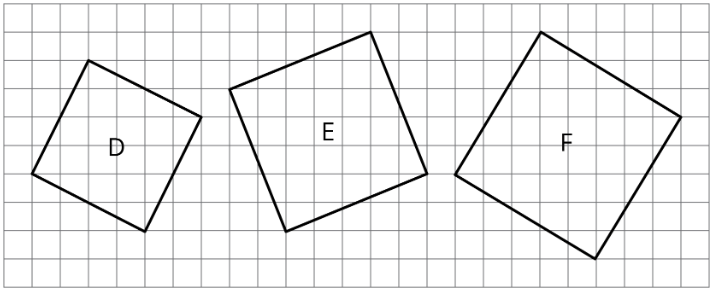
    clipboard_e76d0c62bd8ed6601d9c940f62b723e36.png
    Figura\(\PageIndex{7}\)

    Ejercicio\(\PageIndex{4}\): Making Squares

    Utilice el applet para determinar el área total de las cinco formas\(D\),\(E\),\(F\),\(G\), y\(H\). Supongamos que cada cuadrado pequeño es igual a 1 unidad cuadrada.

    Resumen

    El área de un cuadrado con longitud lateral 12 unidades es\(12^{2}\) o 144 unidades 2.

    La longitud lateral de un cuadrado con área 900 unidades 2 es de 30 unidades porque\(30^{2}=900\).

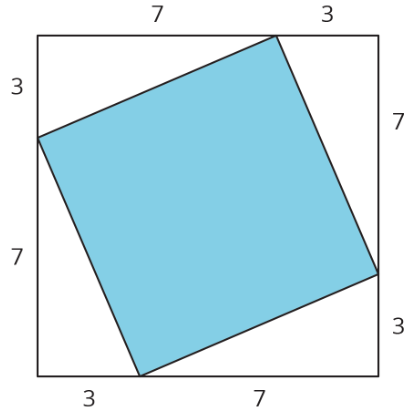
    A veces queremos encontrar el área de una plaza pero no sabemos la longitud lateral. Por ejemplo, ¿cómo podemos encontrar el área de cuadrado\(ABCD\)?

    Una forma es encerrarla en un cuadrado cuyas longitudes laterales sí conocemos.

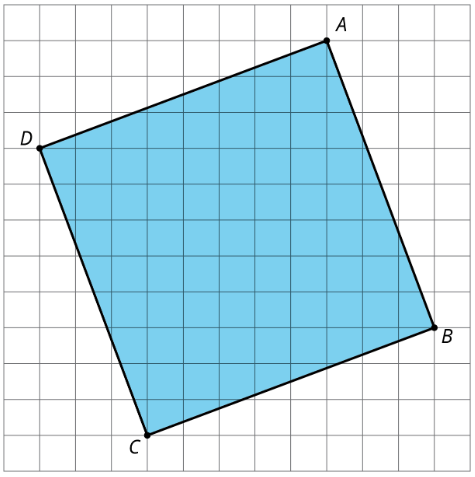
    clipboard_ef106a1661ee02087ae8a395bb8ce10b8.png
    Figura\(\PageIndex{8}\)

    El cuadrado exterior\(EFGH\) tiene longitudes laterales de 11 unidades, por lo que su área es de 121 unidades 2. El área de cada uno de los cuatro triángulos es\(\frac{1}{2}\cdot 8\cdot 3=12\), por lo que el área de los cuatro juntos es\(4\cdot 12=48\) unidades 2. Para obtener el área de la plaza sombreada, podemos tomar el área de la plaza exterior y restar las áreas de los 4 triángulos. Entonces el área del cuadrado sombreado\(ABCD\) es\(121-48=73\) o 73 unidades 2.

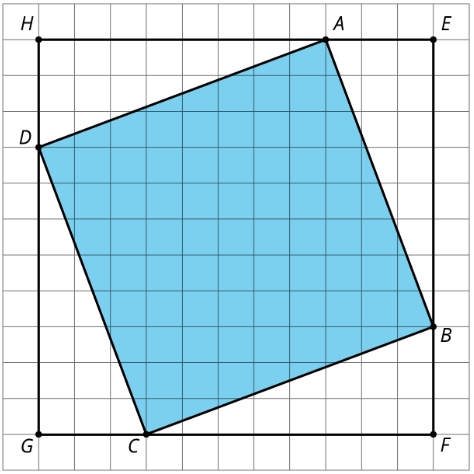
    clipboard_e9286cea23b8ab9673554a67f61f94c56.png
    Figura\(\PageIndex{9}\)

    Practica

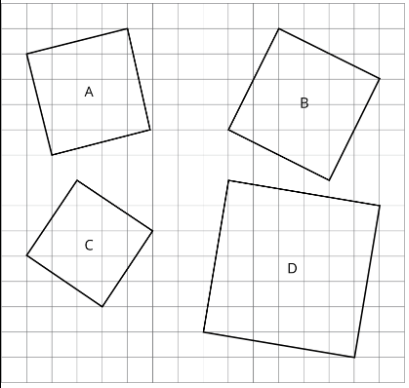
    Ejercicio\(\PageIndex{5}\)

    Encuentra el área de cada plaza. Cada cuadrado de rejilla presenta 1 unidad cuadrada.

    clipboard_ed8950136ecf2172bab12f214c6bcb0b1.png
    Figura\(\PageIndex{10}\)

    Ejercicio\(\PageIndex{6}\)

    Encuentra la longitud de un lado de un cuadrado si su área es:

    1. \(81\)pulgadas cuadradas
    2. \(\frac{4}{25}\)cm 2
    3. \(0.49\)unidades cuadradas
    4. \(m^{2}\)unidades cuadradas

    Ejercicio\(\PageIndex{7}\)

    Encuentra el área de un cuadrado si su longitud lateral es:

    1. 3 pulgadas
    2. 7 unidades
    3. 100 cm
    4. 40 pulgadas
    5. \(x\)unidades

    Ejercicio\(\PageIndex{8}\)

    Evaluar\((3.1\times 10^{4})\cdot (2\times 10^{6})\). Elige la respuesta correcta.

    1. \(5.1\times 10^{10}\)
    2. \(5.1\times 10^{24}\)
    3. \(6.2\times 10^{10}\)
    4. \(6.2\times 10^{24}\)

    (De la Unidad 7.3.6)

    Ejercicio\(\PageIndex{9}\)

    Noé lee el problema: “Evaluar cada expresión, dando la respuesta en notación científica”. La primera parte problemática es:\(5.4\times 10^{5}+2.3\times 10^{4}\).

    Noé dice: “Puedo reescribir\(5.4\times 10^{5}\) como\(54\times 10^{4}\). Ahora puedo agregar los números:\(54\times 10^{4}+2.3\times 10^{4}=57.3\times 10^{4}\).”

    ¿Estás de acuerdo con la solución de Noé al problema? Explica tu razonamiento.

    (De la Unidad 7.3.7)

    Ejercicio\(\PageIndex{10}\)

    Seleccione todas las expresiones que sean equivalentes a\(3^{8}\).

    1. \((3^{2})^{4}\)
    2. \(8^{3}\)
    3. \(3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\)
    4. \((3^{4})^{2}\)
    5. \(\frac{3^{6}}{3^{-2}}\)
    6. \(3^{6}\cdot 10^{2}\)

    (De la Unidad 7.2.5)

    This page titled 8.1.1: Las áreas de los cuadrados y sus longitudes laterales is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.