8.2.6: Encontrar distancias en el plano de coordenadas

Lección

Busquemos distancias en el plano de coordenadas.

Ejercicio\(\PageIndex{1}\): Closest Distance

1. Ordene los siguientes pares de coordenadas del más cercano al más alejado. Esté preparado para explicar su razonamiento.
   1. \((2,4)\)y\((2,10)\)
   2. \((-3,6)\)y\((5,6)\)
   3. \((-12,-12)\)y\((-12,-1)\)
   4. \((7,0)\)y\((7,-9)\)
   5. \((1,-10)\)y\((-4,-10)\)
2. Nombra otro par de coordenadas que estarían más juntas que el primer par de tu lista.
3. Nombra otro par de coordenadas que estarían más separadas que el último par de tu lista.

Ejercicio\(\PageIndex{2}\): How Far Apart?

Encuentra las distancias entre los tres puntos mostrados.

Figura\(\PageIndex{1}\)

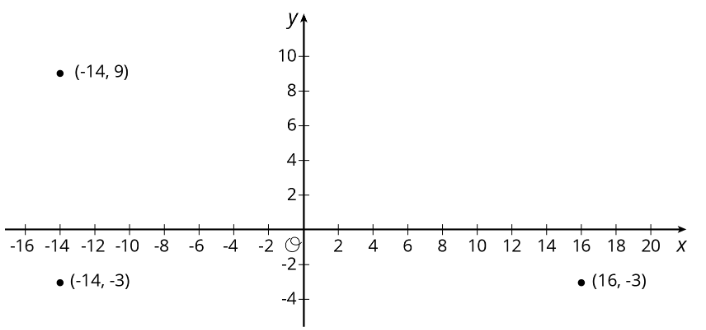
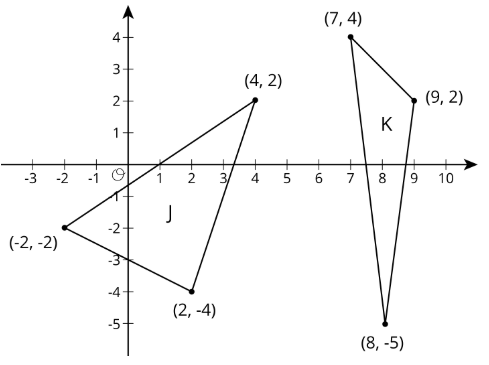
Ejercicio\(\PageIndex{3}\): Perimeters with Pythagoras

1. ¿Cuál figura crees que tiene el perímetro más largo?
2. Seleccione una figura y calcule su perímetro. Tu pareja calculará el perímetro del otro. ¿Tenías razón sobre qué figura tenía el perímetro más largo?

Figura\(\PageIndex{2}\)

¿Estás listo para más?

El cuadrilátero\(ABCD\) tiene vértices en\(A=(-5,1),\: B=(-4,4),\: C=(2,2)\), y\(D=(1,-1)\).

1. Usa el Teorema de Pitágoras para encontrar las longitudes de los lados\(AB\),\(BC\),\(CD\), y\(AD\).
2. Usa el Teorema de Pitágoras para encontrar las longitudes de las dos diagonales,\(AC\) y\(BD\).
3. Explica por qué el cuadrilátero\(ABCD\) es un rectángulo.

Ejercicio\(\PageIndex{4}\): Finding the Right Distance

Haga que cada persona de su grupo seleccione uno de los conjuntos de pares de coordenadas que se muestran aquí. Después calcula la longitud del segmento de línea entre esas dos coordenadas. Una vez calculados los valores, haga que cada persona del grupo comparta brevemente cómo hicieron sus cálculos.

• \((-3,1)\)y\((5,7)\)
• \((-1,-6)\)y\((5,2)\)
• \((-1,-2)\)y\((5,-6)\)
• \((-2,-5)\)y\((6,1)\)

1. ¿Cómo se compara el valor que encontraste con el resto de tu grupo?
2. En sus propias palabras, escriba una explicación a otro estudiante sobre cómo encontrar la distancia entre dos pares de coordenadas cualesquiera.

Resumen

Podemos usar el Teorema de Pitágoras para encontrar la distancia entre dos puntos cualesquiera en el plano de coordenadas. Por ejemplo, si las coordenadas de punto\(A\) son\((-2,-3)\), y las coordenadas de punto\(B\) son\((-8,4)\), encontremos la distancia entre ellas. Esta distancia es también la longitud del segmento de línea\(AB\). Es una buena idea trazar primero los puntos.

Figura\(\PageIndex{3}\)

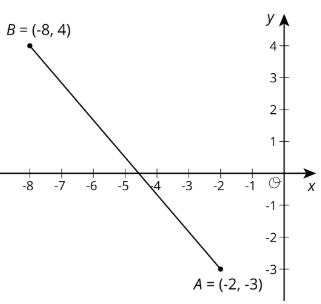
Piense en la distancia entre\(A\) y\(B\), o la longitud del segmento\(AB\), como la hipotenusa de un triángulo rectángulo. Las longitudes de las patas se pueden deducir a partir de las coordenadas de los puntos.

Figura\(\PageIndex{4}\)

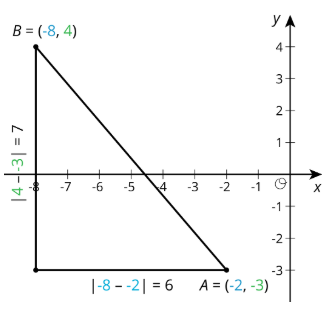
La longitud de la pata horizontal es 6, que se puede ver en el diagrama, pero también es la distancia entre las\(x\) coordenadas -de\(A\) y\(B\) desde\(|-8--2|=6\). La longitud de la pata vertical es de 7, lo que se puede ver en el diagrama, pero esta es también la distancia entre las\(y\) coordenadas -de\(A\) y\(B\) desde\(|-4--3|=7\).

Una vez que se conocen las longitudes de las piernas, utilizamos el Teorema de Pitágoras para encontrar la longitud de la hipotenusa\(AB\), con la que podemos representar\(c\). Dado que\(c\) es un número positivo, solo hay un valor que puede tomar:

\[\begin{aligned} 6^{2}+7^{2}&=c^{2}\\ 36+49&=c^{2}\\ 85&=c^{2} \\ \sqrt{85}&=c\end{aligned}\nonumber\]

Esta longitud es un poco mayor que 9, ya que 85 es un poco más larga que 81. El uso de una calculadora da una respuesta más precisa,\(\sqrt{85}\approx 9.22\).

Entradas en el glosario

Definición: Teorema de Pitágoras

El Teorema de Pitágoras describe la relación entre las longitudes laterales de los triángulos rectos.

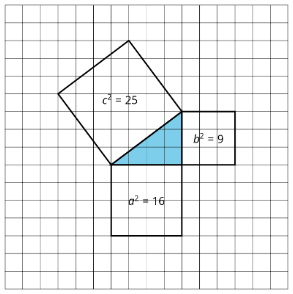
El diagrama muestra un triángulo rectángulo con cuadrados construidos a cada lado. Si agregamos las áreas de los dos cuadrados pequeños, obtenemos el área del cuadrado más grande.

El cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. Esto está escrito como\(a^{2}+b^{2}=c^{2}\).

Figura\(\PageIndex{5}\)

Definición: Hipotenusa

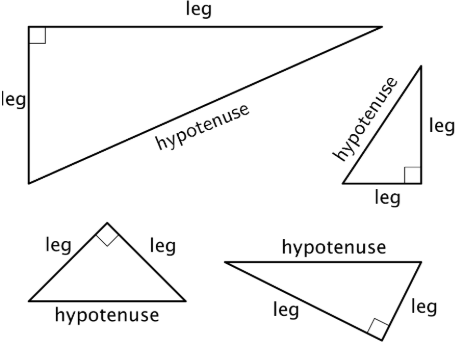
La hipotenusa es el lado de un triángulo rectángulo que está opuesto al ángulo recto. Es el lado más largo de un triángulo rectángulo.

Aquí hay algunos triángulos rectos. Cada hipotenusa está etiquetada.

Figura\(\PageIndex{6}\)

Definición: LEG

Las patas de un triángulo rectángulo son los lados que forman el ángulo recto.

Aquí hay algunos triángulos rectos. Cada pata está etiquetada.

Figura\(\PageIndex{7}\)

Practica

Ejercicio\(\PageIndex{5}\)

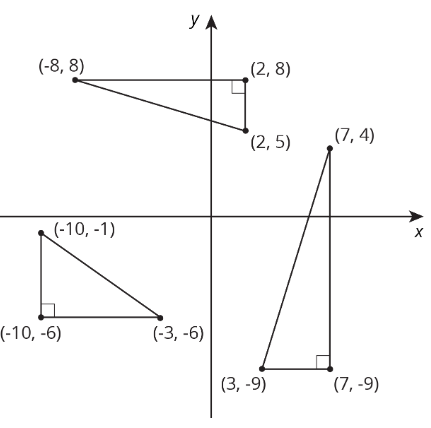
Los triángulos rectos se dibujan en el plano de coordenadas y se etiquetan las coordenadas de sus vértices. Para cada triángulo rectángulo, etiquete cada pata con su longitud.

Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{6}\)

Encuentra la distancia entre cada par de puntos. Si te quedas atascado, intenta trazar los puntos en papel cuadriculado.

1. \(M=(0,-11)\)y\(P=(0,2)\)
2. \(A=(0,0)\)y\(B=(-3,-4)\)
3. \(C=(9,0)\)y\(D=(0,-6)\)

Ejercicio\(\PageIndex{7}\)

1. Encuentra un objeto que contenga un ángulo recto. Esto puede ser algo en la naturaleza o algo que fue hecho por humanos o máquinas.
2. Mida los dos lados que forman el ángulo recto. Luego mida la distancia desde el extremo de un lado hasta el extremo del otro.
3. Dibuja un diagrama del objeto, incluyendo las medidas.
4. Usa el Teorema de Pitágoras para demostrar que tu objeto realmente tiene un ángulo recto.

(De la Unidad 8.2.4)

Ejercicio\(\PageIndex{8}\)

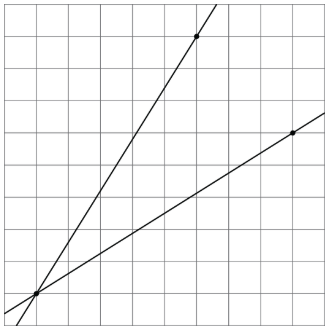
¿Qué línea tiene una pendiente de 0.625 y qué línea tiene una pendiente de 1.6? Explica por qué las pendientes de estas líneas son 0.625 y 1.6.

Figura\(\PageIndex{9}\)

(De la Unidad 2.3.1)

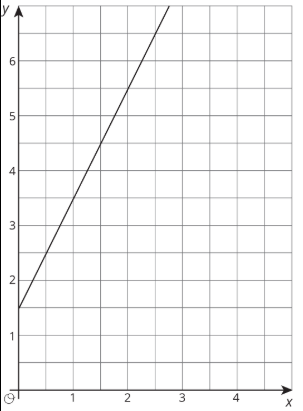
Ejercicio\(\PageIndex{9}\)

Escribe una ecuación para la gráfica.

Figura\(\PageIndex{10}\)

(De la Unidad 3.2.3)