8.2.5: Aplicaciones del Teorema de Pitágoras

Lección

Exploremos algunas aplicaciones del Teorema de Pitágoras.

Ejercicio\(\PageIndex{1}\): Closest Estimate: Square Roots

¿Cuál estimación es la más cercana al valor real de la expresión? Explica tu razonamiento.

1. \(\sqrt{24}\)
   • \(4\)
   • \(4.5\)
   • \(5\)
2. \(\sqrt{7}\)
   • \(2\)
   • \(2.5\)
   • \(3\)
3. \(\sqrt{42}\)
   • \(6\)
   • \(6.5\)
   • \(7\)
4. \(\sqrt{10}+\sqrt{97}\)
   • \(13\)
   • \(13.25\)
   • \(13.5\)

Ejercicio\(\PageIndex{2}\): Cutting Corners

Mai y Tyler estaban parados en una esquina de un gran campo rectangular y decidieron correr hacia la esquina opuesta. Como Mai tenía una bicicleta y Tyler no, pensaron que sería una carrera más justa si Mai cabalgara por la acera que rodea el campo mientras Tyler corría la distancia más corta directamente a través del campo. El campo es de 100 metros de largo y 80 metros de ancho. Tyler puede correr alrededor de 5 metros por segundo, y Mai puede andar en bicicleta a unos 7.5 metros por segundo.

Figura\(\PageIndex{1}\)

1. Antes de hacer algún cálculo, ¿quién crees que ganará? ¿Por cuánto? Explica tu pensamiento.
2. ¿Quién gana? Muestra tu razonamiento.

¿Estás listo para más?

Puede ser necesaria una calculadora para responder a las siguientes preguntas. Respuestas redondas a la centésima más cercana.

1. Si pudieras darle una ventaja al perdedor de la carrera, ¿cuánto tiempo necesitarían para que ambas personas llegaran a la misma hora?
2. Si pudieras hacer que el ganador fuera más lento, ¿qué tan lento necesitarían ir para que ambas personas llegaran al mismo tiempo?

Ejercicio\(\PageIndex{3}\): Internal Dimensions

Aquí hay dos prismas rectangulares:

Figura\(\PageIndex{2}\)

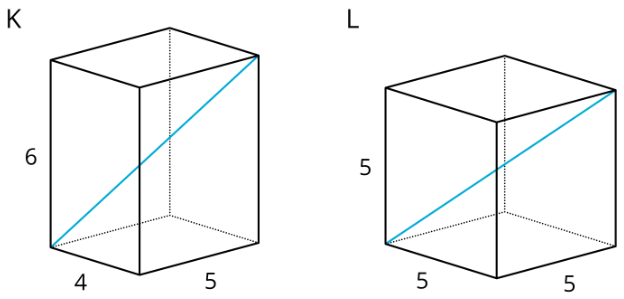
1. ¿Cuál figura crees que tiene la diagonal más larga? Obsérvese que las figuras no están dibujadas a escala.
2. Calcular las longitudes de ambas diagonales. ¿Cuál es en realidad más largo?

Resumen

El Teorema de Pitágoras se puede utilizar para resolver cualquier problema que pueda modelarse con un triángulo rectángulo donde se conocen las longitudes de dos lados y se necesita encontrar la longitud del otro lado. Por ejemplo, digamos que se está colocando un cable en suelo nivelado para soportar una torre. Es un cable de 17 pies, y el cable debe estar conectado 15 pies arriba de la torre. ¿A qué distancia del fondo de la torre debe conectarse el otro extremo del cable al suelo?

A menudo es muy útil dibujar un diagrama de una situación, como el que se muestra aquí:

Figura\(\PageIndex{3}\)

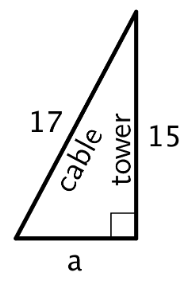
Se supone que la torre hace un ángulo recto con el suelo. Dado que se trata de un triángulo rectángulo, la relación entre sus lados es\(a^{2}+b^{2}=c^{2}\), donde\(c\) representa la longitud de la hipotenusa\(a\) y y\(b\) representan las longitudes de los otros dos lados. La hipotenusa es el lado opuesto al ángulo recto. Hacer sustituciones da\(a^{2}+15^{2}=17^{2}\). Resolviendo esto por\(a\) da\(a=8\). Entonces, el otro extremo del cable debe conectarse al suelo a 8 pies de distancia del fondo de la torre.

Entradas en el glosario

Definición: Teorema de Pitágoras

El Teorema de Pitágoras describe la relación entre las longitudes laterales de los triángulos rectos.

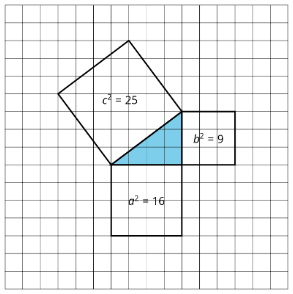
El diagrama muestra un triángulo rectángulo con cuadrados construidos a cada lado. Si agregamos las áreas de los dos cuadrados pequeños, obtenemos el área del cuadrado más grande.

El cuadrado de la hipotenusa es igual a la suma de los cuadrados de las piernas. Esto está escrito como\(a^{2}+b^{2}=c^{2}\).

Figura\(\PageIndex{4}\)

Definición: Hipotenusa

La hipotenusa es el lado de un triángulo rectángulo que está opuesto al ángulo recto. Es el lado más largo de un triángulo rectángulo.

Aquí hay algunos triángulos rectos. Cada hipotenusa está etiquetada.

Figura\(\PageIndex{5}\)

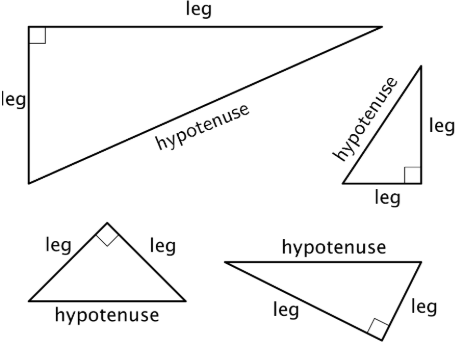
Definición: LEG

Las patas de un triángulo rectángulo son los lados que forman el ángulo recto.

Aquí hay algunos triángulos rectos. Cada pata está etiquetada.

Figura\(\PageIndex{6}\)

Practica

Ejercicio\(\PageIndex{4}\)

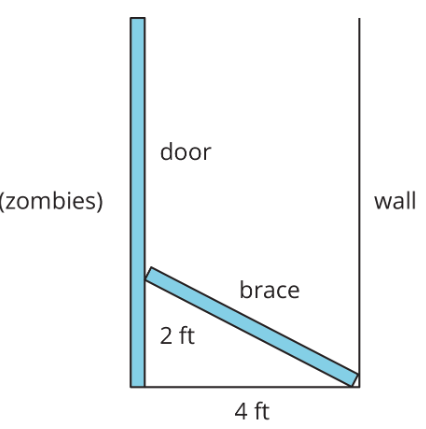
Un hombre está tratando de hacer prueba de zombis en su casa. Quiere cortar un trozo de madera que apunte una puerta contra una pared. El muro está a 4 pies de distancia de la puerta, y quiere que el corsé descanse a 2 pies por la puerta. ¿Acerca de cuánto tiempo debe cortar el corsé?

Figura\(\PageIndex{7}\)

Ejercicio\(\PageIndex{5}\)

En un restaurante, la apertura de un bote de basura es rectangular y mide 7 pulgadas por 9 pulgadas. El restaurante sirve comida en charolas que miden 12 pulgadas por 16 pulgadas. Jada dice que es imposible que la bandeja caiga accidentalmente a través de la abertura del bote de basura porque el lado más corto de la bandeja es más largo que cualquiera de los bordes de la abertura. ¿Estás de acuerdo o en desacuerdo con la explicación de Jada? Explica tu razonamiento.

Ejercicio\(\PageIndex{6}\)

Selecciona todos los conjuntos que son las tres longitudes laterales de los triángulos rectos.

1. \(8,7,15\)
2. \(4,10,\sqrt{84}\)
3. \(\sqrt{8},11,\sqrt{129}\)
4. \(\sqrt{1},2,\sqrt{3}\)

(De la Unidad 8.2.4)

Ejercicio\(\PageIndex{7}\)

Por cada par de números, ¿cuál de los dos números es mayor? ¿Cuántas veces más grandes?

1. \(12\cdot 10^{9}\)y\(4\cdot 10^{9}\)
2. \(1.5\cdot 10^{12}\)y\(3\cdot 10^{12}\)
3. \(20\cdot 10^{4}\)y\(6\cdot 10^{5}\)

(De la Unidad 7.3.2)

Ejercicio\(\PageIndex{8}\)

Una línea contiene el punto\((3,5)\). Si la línea tiene pendiente negativa, ¿cuál de estos puntos podría estar también en la línea?

1. \((2,0)\)
2. \((4,7)\)
3. \((5,4)\)
4. \((6,5)\)

(De la Unidad 3.3.2)

Ejercicio\(\PageIndex{9}\)

Noah y Han se preparan para un concurso de cuerda para saltar. Noé puede saltar 40 veces en 0.5 minutos. Han puede saltar\(y\) tiempos en\(x\) minutos, donde\(y=78x\). Si ambos saltan por 2 minutos, ¿quién salta más veces? ¿Cuántos más?

(De la Unidad 3.1.4)