8.3.2: Raíces cúbicas
- Page ID
- 118626
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lección
Comparemos las raíces cubicas.
Ejercicio\(\PageIndex{1}\): True or False: Cubed
Decidir si cada declaración es verdadera o falsa.
\(\left(\sqrt[3]{5}\right) ^{3}=5\)
\(\left(\sqrt[3]{27}\right)^{3}=3\)
\(7=\left(\sqrt[3]{7}\right)^{3}\)
\(\left(\sqrt[3]{10}\right)^{3}=1,000\)
\(\left(\sqrt[3]{64}\right) = 2^{3}\)
Ejercicio\(\PageIndex{2}\): Cube Root Values
¿Entre qué dos números enteros se encuentra cada raíz cúbica? Esté preparado para explicar su razonamiento.
- \(\sqrt[3]{5}\)
- \(\sqrt[3]{23}\)
- \(\sqrt[3]{81}\)
- \(\sqrt[3]{999}\)
Ejercicio\(\PageIndex{3}\): Solutions on a Number Line
Los números\(x\),\(y\), y\(z\) son positivos, y:
\(x^{3}=5\qquad y^{3}=27\qquad z^{3}=700\)
- Trazar\(x\),\(y\), y\(z\) en la recta numérica. Prepárate para compartir tu razonamiento con la clase.
- Trazar\(-\sqrt[3]{2}\) en la recta numérica.
¿Estás listo para más?
Diego sabe eso\(8^{2}=64\) y aquello\(4^{3}=64\). Dice que esto significa que todos son ciertos los siguientes:
- \(\sqrt{64}=8\)
- \(\sqrt[3]{64}=4\)
- \(\sqrt{-64}\)
- \(\sqrt[3]{-64}\)
¿Está en lo cierto? Explique cómo sabe.
Resumen
Recuerde que las raíces cuadradas de números enteros se definen como longitudes laterales de cuadrados. Por ejemplo,\(\sqrt{17}\) es la longitud lateral de un cuadrado cuya área es 17. Definimos raíces cúbicas de manera similar, pero usando cubos en lugar de cuadrados. El número\(\sqrt[3]{17}\), pronunciado “la raíz cúbica de 17”, es la longitud del borde de un cubo que tiene un volumen de 17.
Podemos aproximar los valores de las raíces cúbicas observando los números enteros a su alrededor y recordando la relación entre las raíces cúbicas y los cubos. Por ejemplo,\(\sqrt[3]{20}\) es entre 2 y 3 ya que\(2^{3}=8\) y\(3^{3}=27\), y 20 es entre 8 y 27. De igual manera, ya que 100 está entre\(4^{3}\) y\(5^{3}\), sabemos que\(\sqrt[3]{100}\) está entre 4 y 5. Muchas calculadoras tienen una función de raíz cúbica que se puede utilizar para aproximar el valor de una raíz cúbica con mayor precisión. Usando nuestros números de antes, una calculadora mostrará eso\(\sqrt[3]{20}\approx 2.7144\) y aquello\(\sqrt[3]{100}\approx 4.6416\).
También como las raíces cuadradas, la mayoría de las raíces cúbicas de números enteros son irracionales. La única vez que la raíz cúbica de un número es un número entero es cuando el número original es un cubo perfecto.
Entradas en el glosario
Definición: Raíz cúbica
La raíz cúbica de un número\(n\) es el número cuyo cubo es\(n\). También es la longitud del borde de un cubo con un volumen de\(n\). Escribimos la raíz cúbica de\(n\) as\(\sqrt[3]{n}\).
Por ejemplo, la raíz cúbica de 64, escrita como\(\sqrt[3]{64}\), es 4 porque\(4^{3}\) es 64. \(\sqrt[3]{64}\)es también la longitud del borde de un cubo que tiene un volumen de 64.
Practica
Ejercicio\(\PageIndex{4}\)
Encuentra la solución positiva a cada ecuación. Si la solución es irracional, escriba la solución usando notación de raíz cuadrada o raíz cúbica.
- \(t^{3}=216\)
- \(a^{2}=15\)
- \(m^{3}=8\)
- \(c^{3}=343\)
- \(f^{3}=181\)
Ejercicio\(\PageIndex{5}\)
Por cada raíz cúbica, encuentra los dos números enteros entre los que se encuentra.
- \(\sqrt[3]{11}\)
- \(\sqrt[3]{80}\)
- \(\sqrt[3]{120}\)
- \(\sqrt[3]{250}\)
Ejercicio\(\PageIndex{6}\)
Ordene los siguientes valores de menor a mayor:
\(\sqrt[3]{530}, \sqrt{48}, \pi ,\sqrt{121},\sqrt[3]{27},\frac{19}{2}\)
Ejercicio\(\PageIndex{7}\)
Seleccione todas las ecuaciones que tengan una solución de\(\frac{2}{7}\)
- \(x^{2}=\frac{2}{7}\)
- \(x^{2}=\frac{4}{14}\)
- \(x^{2}=\frac{4}{49}\)
- \(x^{3}=\frac{6}{21}\)
- \(x^{3}=\frac{8}{343}\)
- \(x^{3}=\frac{6}{7}\)
Ejercicio\(\PageIndex{8}\)
La ecuación\(x^{2}=25\) tiene dos soluciones. Esto se debe a que tanto\(5\cdot 5=25\), como también\(-5\cdot -5=25\). Entonces, 5 es una solución, y también -5 es una solución. ¡Pero! La ecuación\(x^{3}=125\) sólo tiene una solución, que es 5. Esto se debe a que\(5\cdot 5\cdot 5=125\), y no hay otros números que puedas cubo para hacer 125. (¡Piensa por qué -5 no es una solución!)
Encuentra todas las soluciones a cada ecuación.
- \(x^{3}=8\)
- \(\sqrt[3]{x}=3\)
- \(x^{2}=49\)
- \(x^{3}=\frac{64}{125}\)
Ejercicio\(\PageIndex{9}\)
Encuentra el valor de cada variable, a la décima más cercana.
1.
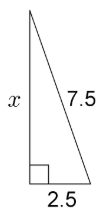
2.
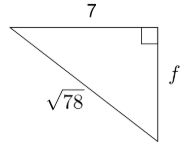
3.
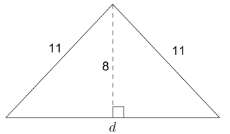
(De la Unidad 8.2.3)
Ejercicio\(\PageIndex{10}\)
Una manzana estándar en Manhattan es un rectángulo que mide 80 m por 270 m. Un residente quiere llegar de una esquina de una cuadra a la esquina opuesta de una manzana que contiene un parque. Ella se pregunta sobre la diferencia entre cortar la diagonal a través del parque en comparación con dar la vuelta al parque, a lo largo de las calles. ¿Cuánto más corto sería su paseo pasando por el parque? Redondea tu respuesta al medidor más cercano.
(De la Unidad 8.2.5)