Saltar al contenido principal
LibreTexts Español

8.4.1: Representación decimal de números racionales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118614

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lección

    Aprendamos más sobre cómo se pueden representar los números racionales.

    Ejercicio\(\PageIndex{1}\): Notice and Wonder: Shaded Bars

    ¿Qué notas? ¿Qué te preguntas?

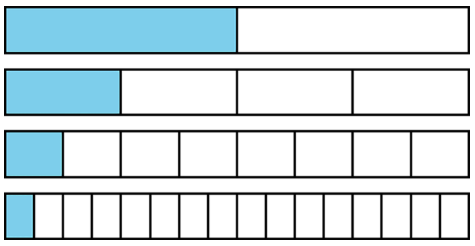
    clipboard_ebcc724cfc86e1143e8d6200d5a4d6220.png
    Figura\(\PageIndex{1}\): Cuatro barras rectangulares de igual longitud, alineadas verticalmente. La primera barra rectangular se divide en dos partes de igual tamaño y la primera parte está sombreada. La segunda barra rectangular se divide en 4 partes de igual tamaño y la primera parte está sombreada. La tercera barra rectangular se divide en 8 partes de igual tamaño y la primera parte está sombreada. La cuarta barra rectangular se divide en 16 partes de igual tamaño y la primera barra está sombreada.

    Ejercicio\(\PageIndex{2}\): Halving The Length

    Aquí hay una línea numéricadel 0 al 1.

    clipboard_ef53680fc0a372d160eb2006114d8e465.png
    Figura\(\PageIndex{2}\)
    1. Marque el punto medio entre 0 y 1. ¿Cuál es la representación decimal de ese número?
    2. Marcar el punto medio entre 0 y el punto más nuevo. ¿Cuál es la representación decimal de ese número?
    3. Repita el paso dos. ¿Cómo encontraste el valor de este número?
    4. Describe cómo el valor de los puntos medios que has agregado a la línea numérica sigue cambiando a medida que encuentras más. ¿Cómo cambian las representaciones decimales?

    Ejercicio\(\PageIndex{3}\): Recalculating Rational Numbers

    1. Los números racionales son fracciones y sus opuestos. Todos estos números son números racionales. Demostrar que son racionales escribiéndolos en la forma\(\frac{a}{b}\) o\(-\frac{a}{b}\).
      1. \(0.2\)
      2. \(-\sqrt{4}\)
      3. \(0.333\)
      4. \(\sqrt[3]{1000}\)
      5. \(-1.000001\)
      6. \(\sqrt{\frac{1}{9}}\)
    2. Todos los números racionales también tienen representaciones decimales. Encuentra la representación decimal de cada uno de estos números racionales.
      1. \(\frac{3}{8}\)
      2. \(\frac{7}{5}\)
      3. \(\frac{999}{1000}\)
      4. \(\frac{111}{2}\)
      5. \(\sqrt[3]{\frac{1}{8}}\)

    Ejercicio\(\PageIndex{4}\): Zooming In On \(\frac{2}{11}\)

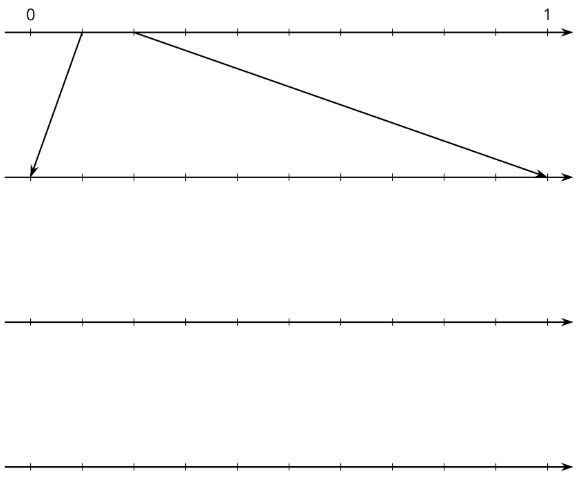
    clipboard_e8407eea3de850efb838836f485685d3e.png
    Figura\(\PageIndex{3}\)
    1. En la línea numérica superior, etiquete las marcas de garrapata. A continuación, busque el primer lugar decimal de\(\frac{2}{11}\) usar división larga y estime dónde\(\frac{2}{11}\) debe colocarse en la línea numérica superior.
    2. Etiquete las marcas de la segunda línea numérica. Encuentre el siguiente lugar decimal de\(\frac{2}{11}\) continuando la división larga y estime dónde\(\frac{2}{11}\) debe colocarse en la segunda línea numérica. Agregue flechas de la segunda a la tercera línea numérica para acercar la ubicación de\(\frac{2}{11}\).
    3. Repita el paso anterior para las líneas numéricas restantes.
    4. ¿Cuál crees que\(\frac{2}{11}\) es la expansión decimal de?

    ¿Estás listo para más?

    Let\(x=\frac{25}{11}=2.272727\ldots\) y\(y=\frac{58}{33}=1.75757575\ldots\)

    Para cada una de las siguientes preguntas, primero decida si la fracción o las representaciones decimales de los números son más útiles para responder a la pregunta, y luego encontrar la respuesta.

    • ¿Cuál de\(x\) o\(y\) está más cerca de 2?
    • Encuentra\(x^{2}\).

    Resumen

    Aprendimos antes que los números racionales son una fracción o lo contrario de una fracción. Por ejemplo,\(\frac{3}{4}\) y\(-\frac{5}{2}\) son ambos números racionales. Una expresión numérica de aspecto complicado también puede ser un número racional siempre que el valor de la expresión sea una fracción positiva o negativa. Por ejemplo,\(\sqrt{64}\) y\(-\sqrt[3]{\frac{1}{8}}\) son números racionales porque\(\sqrt{64}=8\) y\(-\sqrt[3]{\frac{1}{8}}=-\frac{1}{2}\).

    Los números racionales también se pueden escribir usando notación decimal. Algunos tienen expansiones decimales finitas, como 0.75, -2.5 o -0.5. Otros números racionales tienen expansiones decimales infinitas, como 0.7434343.. donde los 43 se repiten para siempre. Para evitar escribir la parte repetida una y otra vez, usamos la notación\(0.7\overline{43}\) para este número. El listón sobre parte de la expansión nos dice la parte que va a repetir para siempre.

    Una expansión decimal de un número nos ayuda a trazarlo con precisión en una recta numérica dividida en décimas. Por ejemplo,\(0.7\overline{43}\) debe estar entre 0.7 y 0.8. Cada dígito decimal adicional aumenta la precisión de nuestro trazado. Por ejemplo, el número\(0.7\overline{43}\) está entre 0.743 y 0.744.

    Entradas en el glosario

    Definición: Decimal repetido

    Un decimal repetido tiene dígitos que siguen en el mismo patrón una y otra vez. Los dígitos repetidos están marcados con una línea encima de ellos.

    Por ejemplo, la representación decimal para\(\frac{1}{3}\) is\(0.\overline{3}\), que significa 0.3333333. La representación decimal para\(\frac{25}{22}\) es la\(1.1\overline{36}\) que significa 1.136363636.

    Practica

    Ejercicio\(\PageIndex{5}\)

    Andre y Jada están discutiendo cómo escribir\(\frac{17}{20}\) como decimal.

    Andre dice que puede usar división larga para dividir\(17\) por\(20\) para obtener el decimal.

    Jada dice que puede escribir una fracción equivalente con un denominador de\(100\) multiplicando por\(\frac{5}{5}\), luego escribiendo el número de centésimas como decimal.

    1. ¿Funcionan ambas estrategias?
    2. ¿Qué estrategia prefieres? Explica tu razonamiento.
    3. Escribir\(\frac{17}{20}\) como decimal. Explica o muestra tu razonamiento.

    Ejercicio\(\PageIndex{6}\)

    Escribe cada fracción como decimal.

    1. \(\sqrt{\frac{9}{100}}\)
    2. \(\frac{99}{100}\)
    3. \(\sqrt{\frac{9}{16}}\)
    4. \(\frac{23}{10}\)

    Ejercicio\(\PageIndex{7}\)

    Escribe cada decimal como una fracción.

    1. \(\sqrt{0.81}\)
    2. \(0.0276\)
    3. \(\sqrt{0.04}\)
    4. \(10.01\)

    Ejercicio\(\PageIndex{8}\)

    Encuentra la solución positiva a cada ecuación. Si la solución es irracional, escriba la solución usando notación de raíz cuadrada o raíz cubo.

    1. \(x^{2}=90\)
    2. \(p^{3}=90\)
    3. \(z^{2}=1\)
    4. \(y^{3}=1\)
    5. \(w^{2}=36\)
    6. \(h^{3}=64\)

    (De la Unidad 8.3.2)

    Ejercicio\(\PageIndex{9}\)

    Aquí hay una pirámide cuadrada derecha.

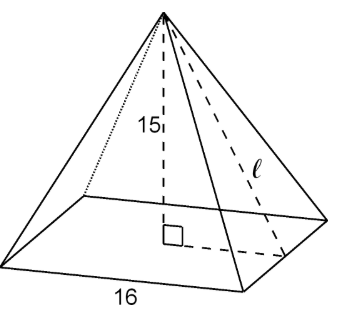
    clipboard_e7b337ccff2727ce712105079d5652928.png
    Figura\(\PageIndex{4}\)
    1. ¿Cuál es la medida de la altura inclinada\(l\) de la cara triangular de la pirámide? Si te quedas atascado, usa una sección transversal de la pirámide.
    2. ¿Cuál es la superficie de la pirámide?

    (De la Unidad 8.2.5)

    This page titled 8.4.1: Representación decimal de números racionales is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.