8.4.2: Expansiones Decimales Infinitas

Lección

Pensemos en decimales infinitos.

Ejercicio\(\PageIndex{1}\): Searching for Digits

Se\(\frac{3}{7}\) han calculado los primeros 3 dígitos después del decimal para la expansión decimal de. Encuentra los siguientes 4 dígitos.

Figura\(\PageIndex{1}\)

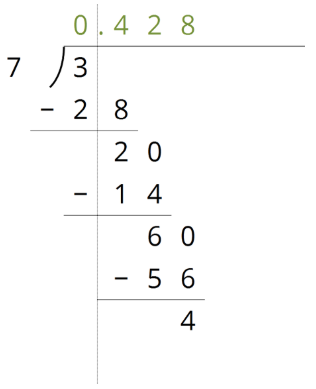
Ejercicio\(\PageIndex{2}\): Some Numbers are Rational

Tu profesor le dará a tu grupo un juego de tarjetas. Cada tarjeta tendrá un lado de cálculos y un lado de explicación.

1. Las tarjetas muestran el trabajo de Noé calculando la representación fraccional de\(0.4\overline{85}\). Arregla estos para ver cómo se dio cuenta de eso\(0.4\overline{85}=\frac{481}{990}\) sin necesidad de una calculadora.
2. Usa el método de Noé para calcular la representación de fracciones de:
   1. \(0.1\overline{86}\)
   2. \(0.7\overline{88}\)

¿Estás listo para más?

Utilice esta técnica para encontrar representaciones fraccionarias para\(0.\overline{3}\) y\(0.\overline{9}\).

Ejercicio\(\PageIndex{3}\): Some Numbers are Not Rational

1.

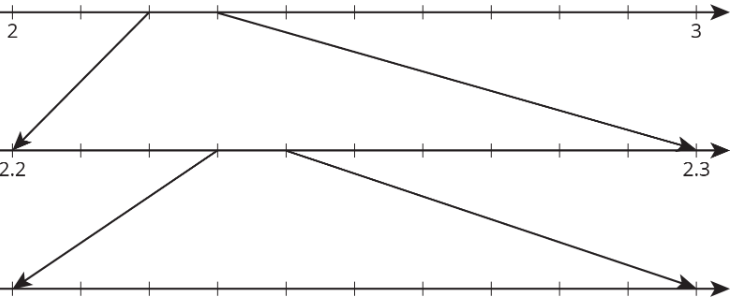
1. ¿Por qué está\(\sqrt{2}\) entre 1 y 2 en la recta numérica?
2. ¿Por qué está\(\sqrt{2}\) entre 1.4 y 1.5 en la recta numérica?
3. ¿Cómo se puede calcular una aproximación para una\(\sqrt{2}\) precisión de 3 decimales?
4. Etiquete todas las marcas de garrapata. Trazar\(\sqrt{2}\) en las tres líneas de números. Asegúrate de agregar flechas de la segunda a la tercera línea numérica.

Figura\(\PageIndex{2}\)

2.

1. Elena nota que un vaso de precipitados en clase de ciencias dice que tiene un diámetro de 9 cm y mide su circunferencia para ser de 28.3 cm. ¿Qué valor obtienes por\(\pi\) usar estos valores y la ecuación para circunferencia,\(C=2\pi r\)?
2. Diego se enteró de que uno de los tanques de combustible del transbordador espacial tenía un diámetro de 840 cm y una circunferencia de 2,639 cm. ¿Qué valor obtienes por\(\pi\) usar estos valores y la ecuación para circunferencia,\(C=2\pi r\)?
3. Etiquete todas las marcas de las líneas numéricas. Use una calculadora para obtener una aproximación muy precisa\(\pi\) y trazar ese número en las tres líneas numéricas.

Figura\(\PageIndex{3}\)

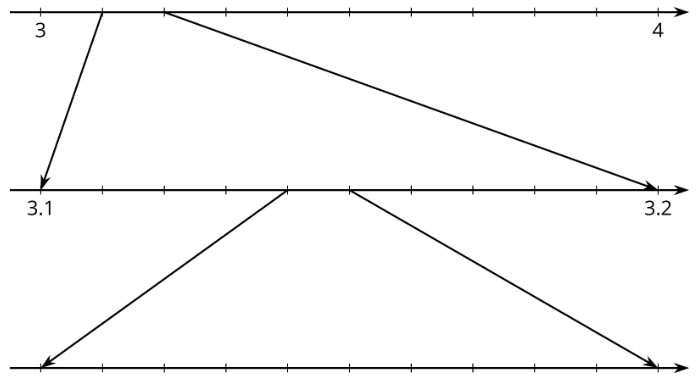
d. ¿Cómo se pueden explicar las diferencias entre estos cálculos de\(\pi\)?

Resumen

No todos los números son racionales. Anteriormente intentamos encontrar una fracción cuyo cuadrado sea igual a 2. Eso resulta imposible, aunque podemos acercarnos bastante (intentar cuadrar\(\frac{7}{5}\)). Ya que no hay fracción igual a\(\sqrt{2}\) ella no es un número racional, razón por la que lo llamamos un número irracional. Otro número irracional bien conocido es\(\pi\).

Cualquier número, racional o irracional, tiene una expansión decimal. A veces dura para siempre. Por ejemplo, el número racional\(\frac{2}{11}\) tiene la expansión decimal\(0.181818\ldots\) con los 18 repitiéndose para siempre. Cada número racional tiene una expansión decimal que o bien se detiene en algún momento o termina en un patrón repetitivo como\(\frac{2}{11}\). Los números irracionales también tienen expansiones decimales infinitas, pero no terminan en un patrón repetitivo. Desde el punto de vista decimal podemos ver que los números racionales son bastante especiales. La mayoría de los números son irracionales, aunque los números que usamos a diario son con mayor frecuencia racionales.

Entradas en el glosario

Definición: Decimal Repitiendo

Un decimal repetido tiene dígitos que siguen en el mismo patrón una y otra vez. Los dígitos repetidos están marcados con una línea encima de ellos.

Por ejemplo, la representación decimal para\(\frac{1}{3}\) is\(0.\overline{3}\), que significa 0.3333333. La representación decimal para\(\frac{25}{22}\) es la\(1.1\overline{36}\) que significa 1.136363636.

Practica

Ejercicio\(\PageIndex{4}\)

Elena y Han están discutiendo cómo escribir el decimal repetido\(x=0.1\overline{37}\) como fracción. Han dice que\(0.1\overline{37}\) es igual\(\frac{13764}{99900}\). “Calculé\(1000x=137.7\overline{77}\) porque el decimal comienza a repetirse después de 3 dígitos. Entonces resté para conseguir\(999x=137.64\). Entonces multiplicé por\(100\) para deshacerme del decimal:\(99900x=13764\). Y finalmente me dividí para conseguir”\(x=\frac{13764}{99900}\). Elena dice que\(0.1\overline{37}\) es igual\(\frac{124}{900}\). “Calculé\(10x=1.37\overline{7}\) porque se repite un dígito. Entonces resté para conseguir\(9x=1.24\). Entonces hice lo que hizo Han para conseguir\(900x=124\) y”\(x=\frac{124}{900}\).

¿Estás de acuerdo con alguno de ellos? Explica tu razonamiento.

Ejercicio\(\PageIndex{5}\)

¿Cómo son los números\(0.444\) y\(0.\overline{4}\) lo mismo? ¿En qué se diferencian?

Ejercicio\(\PageIndex{6}\)

1. Escribe cada fracción como decimal.
   1. \(\frac{2}{3}\)
   2. \(\frac{126}{37}\)
2. Escribe cada decimal como una fracción.
   1. \(0.\overline{75}\)
   2. \(0.\overline{3}\)

Ejercicio\(\PageIndex{7}\)

Escribe cada fracción como decimal.

1. \(\frac{5}{9}\)
2. \(\frac{5}{4}\)
3. \(\frac{48}{99}\)
4. \(\frac{5}{99}\)
5. \(\frac{7}{100}\)
6. \(\frac{53}{90}\)

Ejercicio\(\PageIndex{8}\)

Escribe cada decimal como una fracción.

1. \(0.\overline{7}\)
2. \(0.\overline{2}\)
3. \(0.1\overline{3}\)
4. \(0.\overline{14}\)
5. \(0.\overline{03}\)
6. \(0.6\overline{38}\)
7. \(0.52\overline{4}\)
8. \(0.1\overline{5}\)

Ejercicio\(\PageIndex{9}\)

\(2.2^{2}=4.84\)y\(2.3^{2}=5.29\). Esto da alguna información sobre\(\sqrt{5}\).

Sin calcular directamente la raíz cuadrada, trazar\(\sqrt{5}\) en las tres líneas numéricas usando aproximación sucesiva.

Figura\(\PageIndex{4}\)