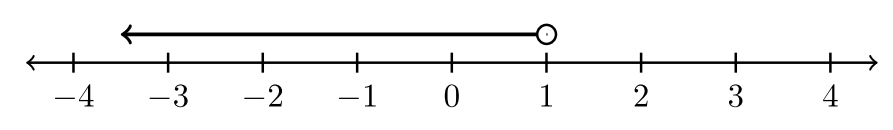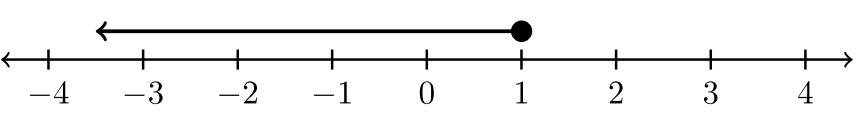4.1: Gráficas de Líneas Numeriales

Última actualización
Guardar como PDF

Page ID: 115861

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Una línea numérica real es un enfoque visual para ordenar todos los números reales:

$clipboard_eb10fd8d4232148ac8dd0aa8dae3d6ba8.png$

Lectura de líneas de números reales

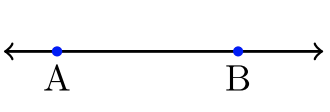
Cualquier número real$A$ trazado a la izquierda de otro número real$B$ tiene la relación:$A < B$, o equivalentemente,$B > A$. Leemos en voz alta, “$A$es menor que$B$” o equivalentemente, “$B$es mayor que”$A$.

Graficando las Desigualdades

“Grafique el conjunto de soluciones”$x > 3$.

La solución puesta a una desigualdad es el conjunto de números reales que hacen de la desigualdad una verdadera declaración. Todos los valores que se encuentran a la derecha de$3$ en la recta numérica son mayores que$3$. El número$3$ en sí no es mayor que$3$. Un gráfico transmite rápidamente el conjunto de soluciones. Para denotar visualmente que no$3$ es mayor que$3$, usaremos un círculo abierto; un círculo que no se llena. La porción azul de esta línea numérica indica valores mayores que$3$.

$clipboard_ebfc0f2306763c3850bb29538d4f4a0f7.png$

Finalmente, desplazamos toda la línea azul por encima de la recta numérica. Ahora no necesitamos colores:

Todos los valores$x > 3$ se representan a continuación:

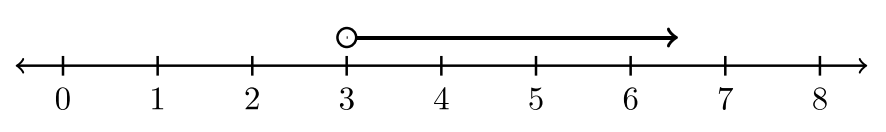
$clipboard_e6f6294b1010f37391ba51ae9b8d08757.png$

Ejemplo 4.1.1

Grafique el conjunto de soluciones$y < 6$.

Solución

El conjunto de soluciones es el conjunto de todos los números reales estrictamente menores que$6$. El gráfico de líneas numéricas transmite la solución:

$clipboard_eedb3bed92075ada5194704602905fa7a.png$

Cómo Decidir: ¿Círculo Cerrado o Abierto?

Desigualdad	Círculo Asociado	Gráficas de ejemplo
\(<\)O bien\(>\)	$clipboard_ea43aad3358d129021fdca988a4b93451.png$	\(x < 1\) $clipboard_e2179e990c1859d0b1b9acd2ab052ee8f.png$
\(≤\)O bien\(≥\)	$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$	\(x ≤ 1\) $clipboard_e074795f922ecf03a8b106d9d7695b5f3.png$

Desigualdad

Círculo Asociado

Gráficas de ejemplo

$<$O bien$>$

$clipboard_ea43aad3358d129021fdca988a4b93451.png$

$x < 1$

$clipboard_e2179e990c1859d0b1b9acd2ab052ee8f.png$

$≤$O bien$≥$

$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$

$x ≤ 1$

$clipboard_e074795f922ecf03a8b106d9d7695b5f3.png$

Ejemplo 4.1.2

Grafique el conjunto de soluciones de$−4 ≤ t$.

Solución

La desigualdad dada es equivalente a$t ≥ −4$. La gráfica expresará todos los valores mayores o iguales a$−4$. En este caso,$−4$ se incluye como solución. Use un círculo relleno para denotar su inclusión en el conjunto de soluciones.

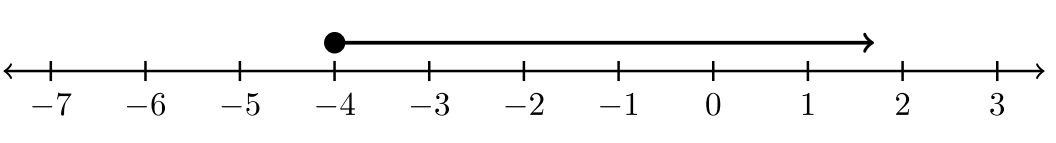
$clipboard_eb6035ca22d56d66675b9bc696be5f336.png$

Todos los valores entre A y B: Desigualdades compuestas

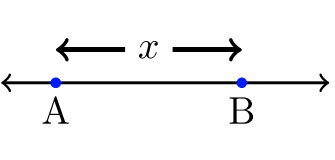
Si queremos describir todos los números entre$A$ y$B$, hay una manera elegante de hacerlo. Deje que$x =$ todos los números reales entre$A$ y$B$. Los ejemplos a continuación utilizan$A = –2$ y$B = 3$. Los círculos abiertos y cerrados corresponden con la desigualdad apropiada.

$clipboard_ea634df7b7e966ecb743ed21413e2739e.png$

Desigualdad	Gráfica
$– 2 < x < 3$	$clipboard_e3e39a5b7387f45cc60b2e0d437998dc7.png$
$– 2 < x ≤ 3$	$clipboard_e0d8d8c2fcc49d6506480180809899351.png$
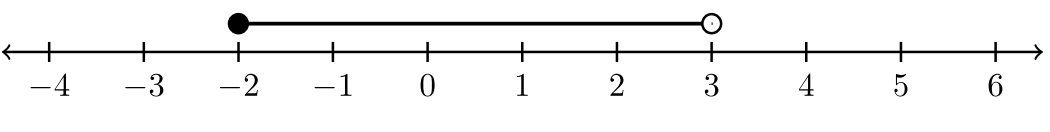$– 2 ≤ x < 3$	$clipboard_e35d9ff4f3e2ab21e4e343006e841b52a.png$
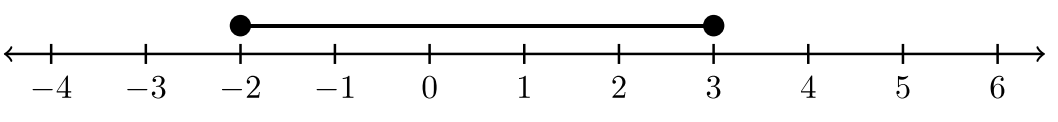$−2 ≤ x ≤ 3$	$clipboard_e5204894c7b49fb5e550d60983085c015.png$

Estas desigualdades no se manejan de manera diferente, sin embargo, la unidad es$π$:

Desigualdad	Gráfica
$– 2 \pi ≤ x ≤ 2 \pi$	$clipboard_e926b79b7a8937c51efd133840e251438.png$
$−4 \pi ≤ x < 0$	$clipboard_eabb4d333641bad8589c5f5a76a801838.png$
$0 < x ≤ 3 \pi$	$clipboard_eb815396b29d68e467172d7a2eb512fbb.png$
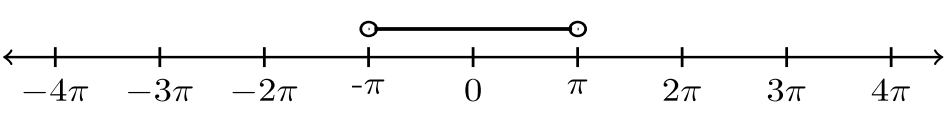$−\pi < x < \pi$	$clipboard_e15a0ce01cdd917bf7082815f958748d7.png$

Desigualdades compuestas

Las desigualdades anteriores son ejemplos de desigualdades compuestas: desigualdades que expresan dos o más desigualdades a la vez. Podemos dividir cada desigualdad arriba en dos desigualdades, usando una declaración “y” entre cada desigualdad:

$A < x < B$es equivalente a$A < x$ y$x < B$

Aviso$A < B$. Cuando las desigualdades están desacopladas, la variable media se expresa en ambas desigualdades, y se mantiene el símbolo de desigualdad.

Repasaremos las desigualdades compuestas en el contexto de las desigualdades de valor absoluto en la Sección 4.4.

Ejemplo 4.1.3

Grafique el conjunto de soluciones de la desigualdad compuesta:$x > −6$ y$x ≤ 0$.

Solución

Las dos desigualdades tienen una afirmación de “y” entre ellas. La primera desigualdad$x > −6$ puede replantearse en su forma equivalente:$−6 < x$. El valor real$A = −6$ es el punto final izquierdo, mientras que$B = 0$ es el extremo derecho. La gráfica se muestra a continuación para$−6 < x ≤ 0$.

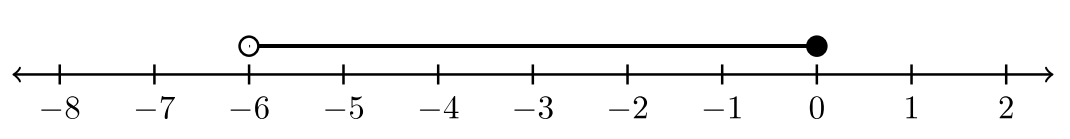
$clipboard_e968d112f5b83c85b858ce9064e330214.png$

¡Pruébalo! (Ejercicios)

Para los ejercicios #1 -10, indicar la desigualdad que está representada por la gráfica.

Desigualdad	Gráfica
1.	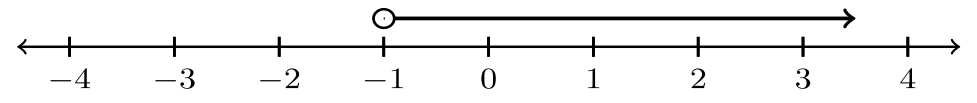$clipboard_e00924fa3af0f2fcd83ccacd00af5647d.png$
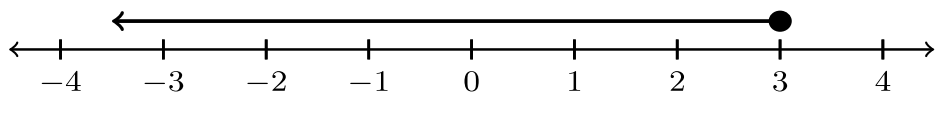2.	$clipboard_e819c87d268a67978cc1a995c2691c4d2.png$
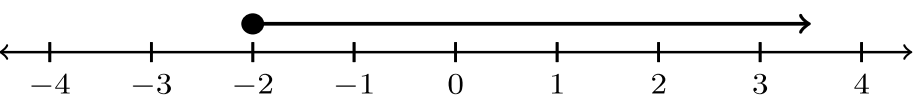3.	$clipboard_ebd297ab3db9d13d2f9afad742edca716.png$
4.	$clipboard_e0a626ad8eb06e627b565e0e1cd960ff6.png$
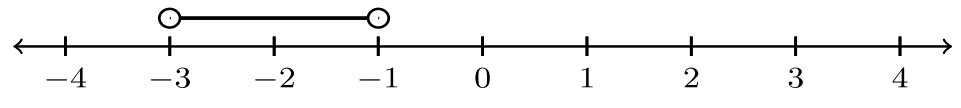5.	$clipboard_ef0134d358695d6c312d5c7bbb69df20d.png$
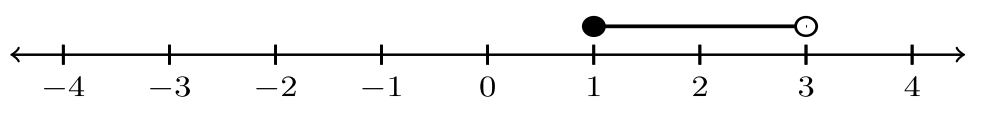6.	$clipboard_e37c51071558f5ec25aa131a5aca372e2.png$
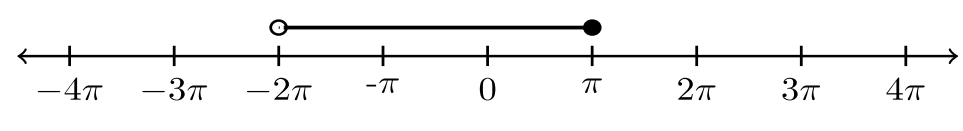7.	$clipboard_e4097966cd968d1434cc3bc3e85a3bf7f.png$
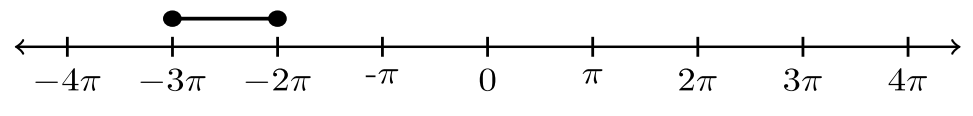8.	$clipboard_e0e80ab3322b0d6cc296a8483012b865b.png$
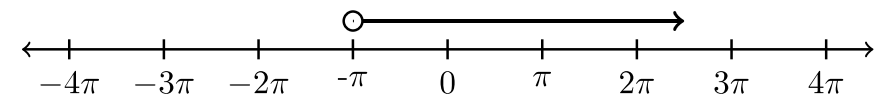9.	$clipboard_e77e211d9d036bbc3a63629dcf396e198.png$
10.	$clipboard_ec81f810d4b5e15b0c0ce633550b6efce.png$

Para los ejercicios #11 -15, la recta numérica se divide por igual. Etiquete las marcas de garrapata. Utilizar fracciones. Después bosquejar el gráfico de líneas numéricos que representa cada desigualdad.

Desigualdad	Gráfica
11. $-\dfrac{1}{2} < x ≤ \dfrac{3}{2}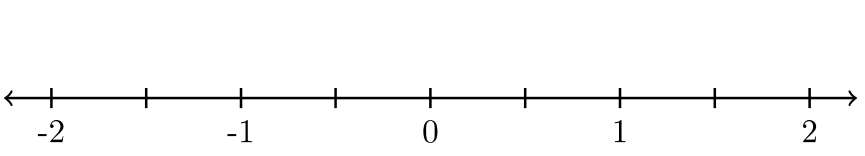$	$clipboard_e8ba383259efa4a68b15faf2313c679cc.png$
12. $x ≥ \dfrac{1}{2}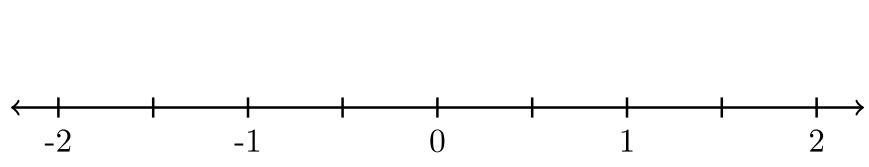$	$clipboard_e7fe4d4e6f1db11432245bc10bf10b34e.png$
13. $x < −\dfrac{3}{2}$	$clipboard_e975beb8cd379a388b26257558781f6c3.png$
14. $−\dfrac{3 \pi}{2} ≤ x < \dfrac{3 \pi}{2}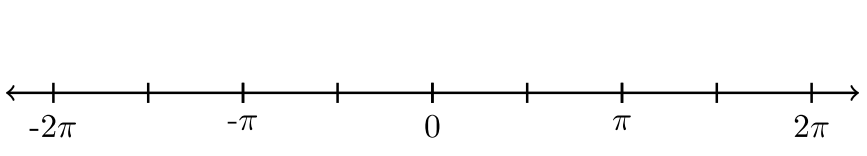$	$clipboard_edff371ef735d6c52249f18a938a354f8.png$
15. $−\dfrac{\pi}{4} < x < \dfrac{3 \pi}{4}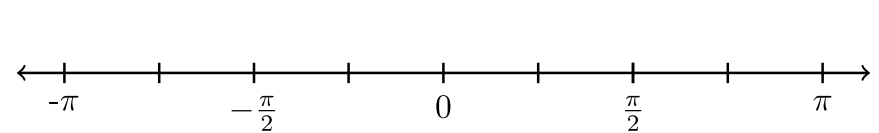$	$clipboard_e63fc7336cdb19c77d1d3401fe5aaaf4d.png$

Para los ejercicios #16 -22, Esboza un gráfico de líneas numéricos que corresponda con la desigualdad compuesta dada.

$x > −2$y$x ≤ 5$
$x ≥ 1$y$x ≤ 10$
$x ≤ −1$y$x > −3$
$x < 8$y$x ≥ −8$
$x > −\dfrac{3}{2}$y$x < \dfrac{1}{2}$
$x ≥ 2 \pi$y$x ≤ 4 \pi$
$x > −\dfrac{\pi}{2}$y$x < \dfrac{\pi}{2}$

Desigualdad	Gráfica
\(– 2 < x < 3\)	$clipboard_e3e39a5b7387f45cc60b2e0d437998dc7.png$
\(– 2 < x ≤ 3\)	$clipboard_e0d8d8c2fcc49d6506480180809899351.png$
\(– 2 ≤ x < 3\)	$clipboard_e35d9ff4f3e2ab21e4e343006e841b52a.png$
\(−2 ≤ x ≤ 3\)	$clipboard_e5204894c7b49fb5e550d60983085c015.png$

Desigualdad	Gráfica
\(– 2 \pi ≤ x ≤ 2 \pi\)	$clipboard_e926b79b7a8937c51efd133840e251438.png$
\(−4 \pi ≤ x < 0\)	$clipboard_eabb4d333641bad8589c5f5a76a801838.png$
\(0 < x ≤ 3 \pi\)	$clipboard_eb815396b29d68e467172d7a2eb512fbb.png$
\(−\pi < x < \pi\)	$clipboard_e15a0ce01cdd917bf7082815f958748d7.png$

Desigualdad	Gráfica
11. \(-\dfrac{1}{2} < x ≤ \dfrac{3}{2}\)	$clipboard_e8ba383259efa4a68b15faf2313c679cc.png$
12. \(x ≥ \dfrac{1}{2}\)	$clipboard_e7fe4d4e6f1db11432245bc10bf10b34e.png$
13. \(x < −\dfrac{3}{2}\)	$clipboard_e975beb8cd379a388b26257558781f6c3.png$
14. \(−\dfrac{3 \pi}{2} ≤ x < \dfrac{3 \pi}{2}\)	$clipboard_edff371ef735d6c52249f18a938a354f8.png$
15. \(−\dfrac{\pi}{4} < x < \dfrac{3 \pi}{4}\)	$clipboard_e63fc7336cdb19c77d1d3401fe5aaaf4d.png$