4.2: Notación de intervalos

Última actualización
Guardar como PDF

Page ID: 115860

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

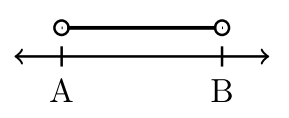
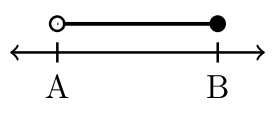
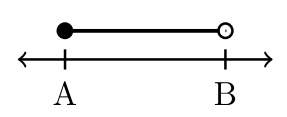
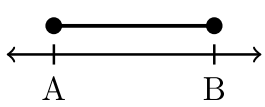
$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Las desigualdades cortan y cortan la recta numérica real en segmentos de interés o intervalos. Un intervalo es un subconjunto continuo e ininterrumpido de números reales. ¿Cómo podemos anotar intervalos con sencillez? La siguiente tabla introduce la notación de intervalos.

Desigualdad	Círculo Asociado	Cierres de punto final asociados
$<$O bien$>$	$clipboard_ea43aad3358d129021fdca988a4b93451.png$	Paréntesis izquierdo: (o paréntesis derecho:)
$≤$O bien$≥$	$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$	Corchete Cuadrado Izquierdo: [o Soporte Cuadrado Derecho:]

Las desigualdades tienen$4$ posibles cierres de intervalos:

$(A,B)$	$(A,B]$	$[A,B)$	$[A,B]$
$clipboard_ef4d418cfbf59895619f0546ad98eaf4f.png$	$clipboard_e510d65b9070b6f966181489fb9235b67.png$	$clipboard_edce393fed1ea667df1f70b28c7dbb00e.png$	$clipboard_e9bbd934e732ad52963b83f2dac9d6bed.png$

El menor número en el intervalo,$A$, siempre se indica primero. Se coloca una coma. El mayor número en el intervalo,$B$, se indica después de la coma. Se considera el cierre apropiado para cada valor$A$ y$B$.

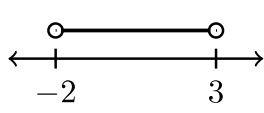
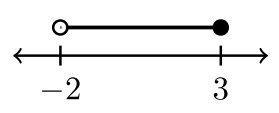
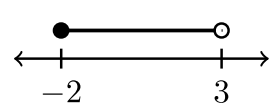
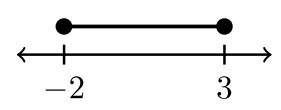
Cuatro ejemplos de notación de intervalos

$−2 < x < 3$	$−2 < x ≤ 3$	$– 2 ≤ x < 3$	$– 2 ≤ x ≤ 3$
$clipboard_eb02fe1b987d2d7aeb60c8fea96ed2803.png$	$clipboard_e019534632b13aa8f1cc8d1d9d3d569d9.png$	$clipboard_edea90ab320a9712b9de1bd8371585e1b.png$	$clipboard_e8b9543e4ca42fb42ac9e7d44a55396c3.png$
$(−2, 3)$	$(−2, 3]$	$[−2, 3)$	$[−2, 3]$

Los Infinidades

Hay dos infinidades: positiva y negativa. Cada uno define una dirección en la recta numérica:

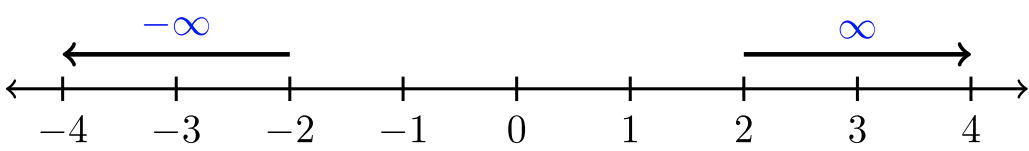
$clipboard_e5b29aa7ac89e2b9ce0b9a83ff14aa23a.png$

El infinito no es un número real. Indica una dirección. Por lo tanto, al usar notación de intervalos, siempre encerrar$∞$ y$−∞$ con paréntesis. Nunca encerramos infinidades con corchete cuadrado.

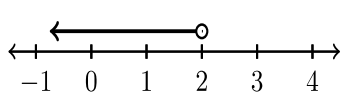
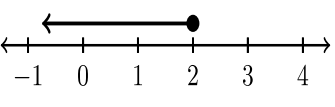
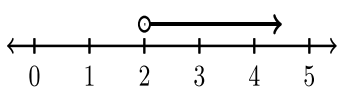
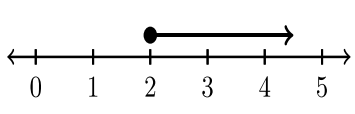
La siguiente tabla muestra cuatro ejemplos de notación de intervalos que requieren el uso de infinito.

$x < 2$	$x ≤ 2$	$x > 2$	$x ≥ 2$
$clipboard_e5734c942cda8d2c4a2fc66d380d43045.png$	$clipboard_e02fd4cce2c4fdbda973bec7ec7cea27d.png$	$clipboard_eaf1970b524b0ed982616d4f351aef523.png$	$clipboard_ed53713ef79ac5f76e978d135bba630af.png$
$(−∞, 2)$	$(−∞, 2]$	$(2, ∞)$	$[2, ∞)$

Combinaciones de Intervalos

Si dos o más intervalos se interrumpen con un hueco en la recta numérica, se utiliza la notación de conjunto para unir los intervalos, simbólicamente. El símbolo que usamos para combinar intervalos es el símbolo de unión:$∪$. La siguiente tabla muestra cuatro ejemplos:

Notación de intervalos	Gráfica
$(−∞, −2) ∪ [1, ∞)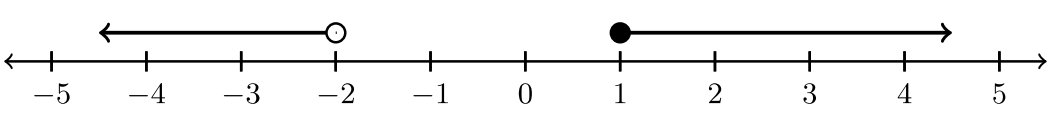$	$clipboard_ee59da9758674b8fbf6ec2276685e5423.png$
$(−∞, −1) ∪ (−1, ∞)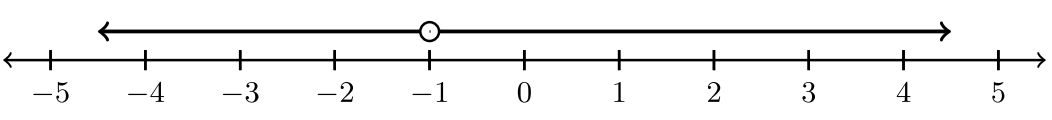$	$clipboard_ed827350d30be0e842f3deae80c6892f7.png$
$\left(−\dfrac{3 \pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left( \dfrac{\pi}{2}, \dfrac{3 \pi}{2} \right)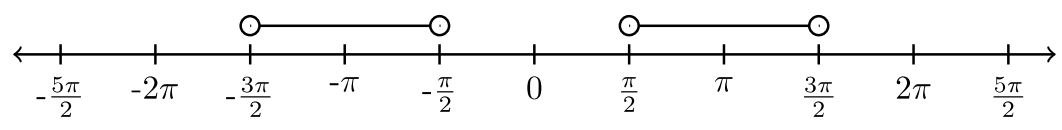$	$clipboard_ebbcf3adffba82a210520564b5a4782e1.png$
$\left[−2 \pi, − \dfrac{\pi}{2} \right) ∪ \left[ \dfrac{3 \pi}{2} , ∞ \right)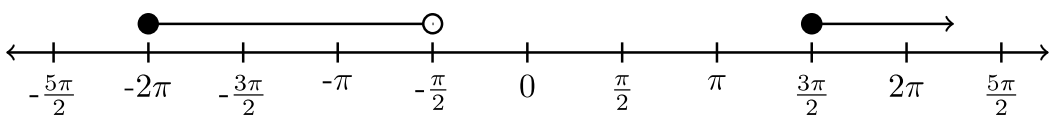$	$clipboard_ef225c28a7a5773a54ade751969064732.png$

Desigualdades compuestas

Los intervalos que tienen brechas, como los mostrados anteriormente, se traducen en desigualdades compuestas. Las soluciones reales pertenecen en un intervalo u otro. La palabra “o” juega un papel clave a la hora de traducir. Por ejemplo: el intervalo$(−∞, −2) ∪ [1, ∞)$ se traduce en su desigualdad compuesta asociada:

$x < -2$o$x ≥ 1$

La palabra “y” no se puede usar entre las desigualdades porque un número no puede pertenecer a ambos intervalos a la vez. Por ejemplo,$x = 5$ es una solución porque$5$ pertenece en el intervalo$x ≥ 1$, pero$5$ no pertenece en el intervalo$x < −2$. Sin embargo, debido a la palabra “o”,$x = 5$ es una solución al intervalo$(−∞, −2) ∪ [1, ∞)$.

¡Pruébalo! (Ejercicios)

Para los ejercicios #1 -6, indique la desigualdad y la notación de intervalo asociada a la gráfica.

Gráfica			Desigualdad	Notación de intervalos
$clipboard_e141ee93db0e0b1fcece04011d50b027c.png$
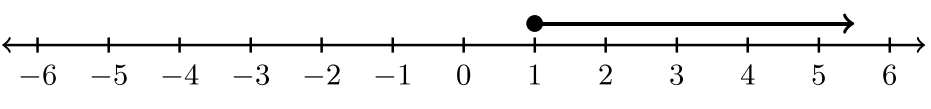$clipboard_ee998ec64608d5197c3eb0225a8dabfb4.png$
$clipboard_e387a79a4c9d9a3c5536f90ca06cc706a.png$
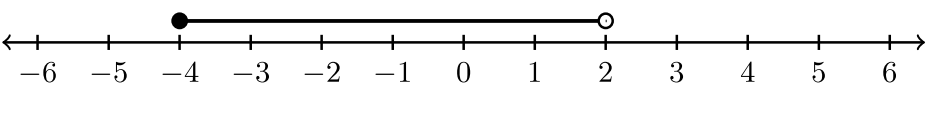$clipboard_e520b9807a5ebbd773c86cc029f9dd4cd.png$
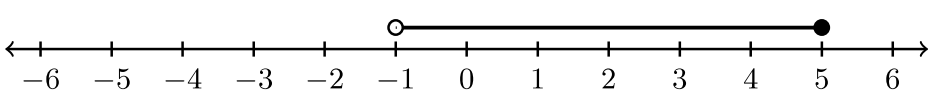$clipboard_e90ef48553dcc2b631e06459ee8b7d36b.png$
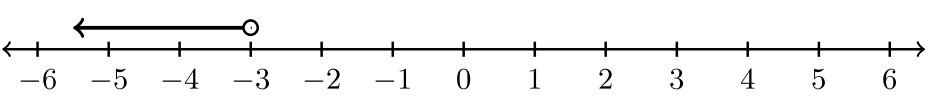$clipboard_e82c969b77994d0dd174ccb04a54f7dec.png$

Para los ejercicios #7 -10, indique la notación del intervalo y esboce la gráfica asociada a la desigualdad.

Gráfica			Desigualdad	Notación de intervalos
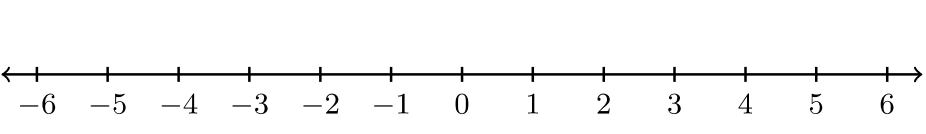$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$−3 ≤ x ≤ 1$
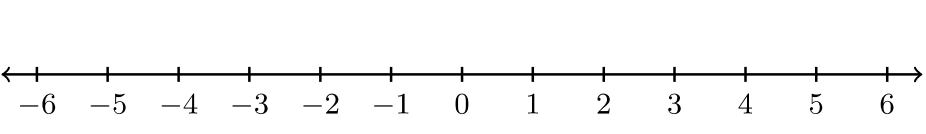$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$x < 4$
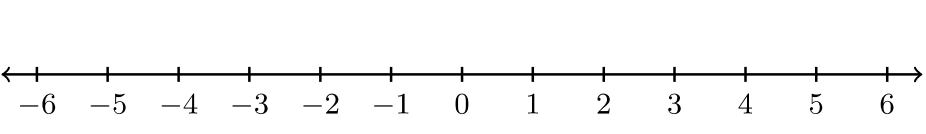$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$x ≥ −2$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$0 ≤ x < 3$

Para los ejercicios #11 -17, bosquejar la gráfica asociada a la notación de intervalo dada.

Gráfica			Notación de intervalos
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, 4)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, −3) ∪ [0, ∞)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$[−1, 1) ∪ [2, ∞)$
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			$(−∞, −5] ∪ (−1, 5)$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$\left[−\dfrac{\pi}{2} , \dfrac{\pi}{2} \right]$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$(−∞, −\pi] ∪ [\pi, ∞)$
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			$\left(−\dfrac{3\pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left(-\dfrac{\pi}{2} , 0\right)$

Para #18 -21

a. Esbozar una gráfica de la desigualdad compuesta.

b. Indicar el intervalo usando notación de intervalo.

$x ≥ 4$o$x ≤ 0$
$x ≤ – 2\pi$o$x > \pi$
$−1 > x$o$2 ≤ x$
$x > 3\pi$o$x < – \pi$

\(−2 < x < 3\)	\(−2 < x ≤ 3\)	\(– 2 ≤ x < 3\)	\(– 2 ≤ x ≤ 3\)
$clipboard_eb02fe1b987d2d7aeb60c8fea96ed2803.png$	$clipboard_e019534632b13aa8f1cc8d1d9d3d569d9.png$	$clipboard_edea90ab320a9712b9de1bd8371585e1b.png$	$clipboard_e8b9543e4ca42fb42ac9e7d44a55396c3.png$
\((−2, 3)\)	\((−2, 3]\)	\([−2, 3)\)	\([−2, 3]\)

\(x < 2\)	\(x ≤ 2\)	\(x > 2\)	\(x ≥ 2\)
$clipboard_e5734c942cda8d2c4a2fc66d380d43045.png$	$clipboard_e02fd4cce2c4fdbda973bec7ec7cea27d.png$	$clipboard_eaf1970b524b0ed982616d4f351aef523.png$	$clipboard_ed53713ef79ac5f76e978d135bba630af.png$
\((−∞, 2)\)	\((−∞, 2]\)	\((2, ∞)\)	\([2, ∞)\)

Search

Text Color

Text Size

Margin Size

Font Type

Desigualdad	Círculo Asociado	Cierres de punto final asociados
\(<\)O bien\(>\)	$clipboard_ea43aad3358d129021fdca988a4b93451.png$	Paréntesis izquierdo: (o paréntesis derecho:)
\(≤\)O bien\(≥\)	$clipboard_e2e4cf904d07dc1241b9e2632c37e681a.png$	Corchete Cuadrado Izquierdo: [o Soporte Cuadrado Derecho:]

\((A,B)\)	\((A,B]\)	\([A,B)\)	\([A,B]\)
$clipboard_ef4d418cfbf59895619f0546ad98eaf4f.png$	$clipboard_e510d65b9070b6f966181489fb9235b67.png$	$clipboard_edce393fed1ea667df1f70b28c7dbb00e.png$	$clipboard_e9bbd934e732ad52963b83f2dac9d6bed.png$

Notación de intervalos	Gráfica
\((−∞, −2) ∪ [1, ∞)\)	$clipboard_ee59da9758674b8fbf6ec2276685e5423.png$
\((−∞, −1) ∪ (−1, ∞)\)	$clipboard_ed827350d30be0e842f3deae80c6892f7.png$
\(\left(−\dfrac{3 \pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left( \dfrac{\pi}{2}, \dfrac{3 \pi}{2} \right)\)	$clipboard_ebbcf3adffba82a210520564b5a4782e1.png$
\(\left[−2 \pi, − \dfrac{\pi}{2} \right) ∪ \left[ \dfrac{3 \pi}{2} , ∞ \right)\)	$clipboard_ef225c28a7a5773a54ade751969064732.png$

Gráfica			Desigualdad	Notación de intervalos
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(−3 ≤ x ≤ 1\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(x < 4\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(x ≥ −2\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\(0 ≤ x < 3\)

Gráfica			Notación de intervalos
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\((−∞, 4)\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\((−∞, −3) ∪ [0, ∞)\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\([−1, 1) ∪ [2, ∞)\)
$clipboard_e6f4396cd9637db53d4e6f58af2818e6b.png$			\((−∞, −5] ∪ (−1, 5)\)
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			\(\left[−\dfrac{\pi}{2} , \dfrac{\pi}{2} \right]\)
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			\((−∞, −\pi] ∪ [\pi, ∞)\)
$clipboard_e1fb276fa8366c7f92f1422621f9dcbef.png$			\(\left(−\dfrac{3\pi}{2} , −\dfrac{\pi}{2} \right) ∪ \left(-\dfrac{\pi}{2} , 0\right)\)