8.1: Secuencias Aritméticas

Última actualización
Guardar como PDF

Page ID: 115921

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La siguiente secuencia de números tiene un patrón que está obligado a reconocer:

$2, 4, 6, 8, 10, 12, 14, 16, 18, …$

Probablemente, describirías la secuencia en palabras: la secuencia de números pares. Alternativamente, ¿podemos describir la secuencia matemáticamente? Es decir, ¿podemos describir el patrón de la secuencia de números pares usando una fórmula? ¡Absolutamente! Esta sección explorará secuencias aritméticas, cómo identificarlas, describir matemáticamente sus términos y la relación entre secuencias aritméticas y funciones lineales. ¡Empecemos!

Definición: Secuencia

Una secuencia es una lista de números:$a_1 , a_2, a_3, a_4 , … , a_n, … $ Una secuencia puede ser una lista finita o infinita. Llamamos$a_1$ al primer término,$a_2$ al segundo término, y$a_n$ al “término general” o al$n^{\text{th}}$ término. Las secuencias tienen un patrón. Describimos el patrón en el término general$a_n$.

Para la secuencia de números pares:$2, 4, 6, 8, 10, …$ el término general$a_n = 2n$.

$clipboard_eddc57d00c36a2fbed49c43f696c7302b.png$

El término general$a_n$ de una secuencia es simplemente una función de$n$, indicado anteriormente como$f(n)$, donde$n$ es un número natural (o número entero si$n$ comienza con cero).

Ejemplo 8.1.1

En la secuencia de números pares, ¿cuál es el$20^{\text{th}}$ término en la secuencia?

Solución

El término general de la secuencia de números pares es$a_n = 2n$. Desde$n =$ el número de término, se nos pide encontrar$a_{20}$.

$\begin{array}&& a_{20} = 2(20) = 40 &\text{Plug in the term-number \(n=20$en la fórmula$a_n=2n$}\ end {array}\)

Respuesta El$20^{\text{th}}$ término de la secuencia de números pares es el número$40$.

Definición: Secuencia aritmética

Si la secuencia:$a_1, a_2, a_3, a_4 , … , a_{n−1}, a_n, …$ exhibe un patrón tal que

\[a_n − a_{n−1} = d\]

Para todos$n$, entonces el número real$d$ se llama la diferencia común, y la secuencia es una secuencia aritmética.

Ejemplo 8.1.2

Se da una secuencia. Si la secuencia es una secuencia aritmética, dar la diferencia común. Si la secuencia no es una secuencia aritmética, explique cómo no puede ser aritmética.

$25, 32, 39, 46, 53, 60, …$
$2, 4, 8, 16, 32, …$
$3^2 , 3^4, 3^6, 3^8, 3^{10}, …$
$0, 1, 0, 1, 0, 1, …$

Solución

Es la secuencia

$25, 32, 39, 46, 53, 60, … $

una secuencia aritmética?

$\begin{array} &a_2 − a_1 &= 32 − 25 &= \textcolor{red}{7} \\ a_3 − a_2 &= 39 − 32 &= \textcolor{red}{7} \\a_4 − a_3 &= 46 − 39 &= \textcolor{red}{7} \\a_5 − a_4 &= 53 − 46 &= \textcolor{red}{7} \\a_6 − a_5 &= 60 − 53 &= \textcolor{red}{7} \end{array}$

La secuencia es aritmética y la diferencia común es$7$.

Es la secuencia

$2, 4, 8, 16, 32, …$

una secuencia aritmética?

$\begin{array} &a_2 − a_1 &= 4 − 2 &= \textcolor{red}{2} \\ a_3 − a_2 &= 8 − 4 &= \textcolor{red}{4} \\a_4 − a_3 &= 16 − 8 &= \textcolor{red}{8} \\a_5 − a_4 &= 32 − 16 &= \textcolor{red}{16} \\ &&\textcolor{red}{2 \neq 4 \neq 8 \neq 16} \end{array}$

La secuencia no es aritmética. $a_n − a_{n-1}$no arroja una diferencia común.

Es la secuencia

$3^2 , 3^4, 3^6, 3^8, 3^{10}, …$

una secuencia aritmética?

$\begin{array} &3^4 − 3^2 &= 3^2 (3^2 − 1) &= 9 \cdot 8 &= \textcolor{red}{72} \\ 3^6 − 3^4 &= 3^4 (3^2 − 1) &= 81 \cdot 8 &= \textcolor{red}{648} \end{array}$

Ya que$a_3 − a_2 \neq a_2 − a_1$, concluimos que la secuencia no es aritmética.

Es la secuencia

$0, 1, 0, 1, 0, 1, …$

una secuencia aritmética?

$\begin{array} 1-0 &= \textcolor{red}{1} \\ 0-1 &= \textcolor{red}{-1} \end{array}$

Ya que$a_3 − a_2 \neq a_2 − a_1$, la secuencia no es aritmética.

Encontrar el término general de una secuencia aritmética

Si una secuencia es aritmética, el término general$a_n$ se determina utilizando la diferencia común,$d$, de la secuencia. Las funciones de la forma$y = mx+b$, conocidas como funciones lineales, tienen una fuerte relación con las secuencias aritméticas. La pendiente$m$ de una función lineal es equivalente a la diferencia común$d$ de una secuencia aritmética. Comparemos secuencias aritméticas con funciones lineales para construir$a_n$, el término general de una secuencia aritmética.

Ejemplo 8.1.3

Encuentra el término general$a_n$ de cada secuencia aritmética:

$4, 7, 10, 13, 16, …$
$100, 80, 60, 40, 20, …$

Solución

Crearemos una tabla de valores para cada secuencia. La primera columna será el número de término,$n$, comenzando con$n = 1$. En la segunda columna se enumerarán los términos de la secuencia. La diferencia común se muestra en el lado de la segunda columna.

La secuencia$4, 7, 10, 13, 16, …$ tiene la diferencia común$d = 3$. Pero también es la pendiente$m$ de la función lineal$f(x) = mx + b$.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{a_n − a_{n-1}}{n − (n − 1))} = \dfrac{d}{1} = d\]

$clipboard_ecbb8d4cf8b9fa5856cc56124c921e2e0.png$

La tabla anterior imita esencialmente cualquier función lineal,$f(x) = mx+b$.

En lugar de$x$, las secuencias usan$n$ valores −.
En lugar de$m =$ pendiente en funciones lineales, las secuencias usan diferencia$d =$ común.
En lugar de$b$, una secuencia indica el mismo valor con$a_0$.

Si$a_1$ denota el primer término de una secuencia, entonces el término general de una secuencia es:

\[a_n = f(n) = d \cdot n + a_0\]

Para encontrar el término general$a_n$,, necesitaremos encontrar el valor$a_0$. Hay varias formas de hacer esto, pero quizás la más simple es crear una fila extra donde$n = 0$, luego usar la diferencia común para encontrar$a_0$. Se mantiene el patrón de diferencia común y$a_0 + d = a_1$.

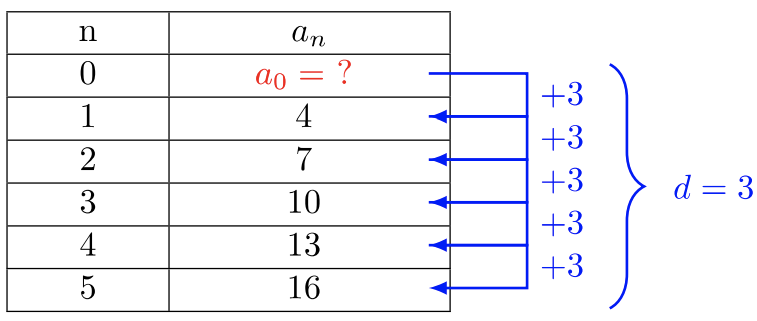
$clipboard_e6eccaea315b268044364f34c0948747d.png$

Encuentra el valor$a_0$:

$\begin{array} &&a_0 + 3 &= 4 \\&a_0 + 3 − 3 &= 4 − 3 \\&a_0 &= 1\end{array}$

El término general de la secuencia es:

$a_n = 3n + 1$

Utilice la misma estrategia para el Ejemplo$8.1.3$ a para resolver el Ejemplo$8.1.3$ b. Crear una tabla, encontrar la diferencia común y encontrar el$a_0$ término de la secuencia$d$$100, 80, 60, 40, 20, …$

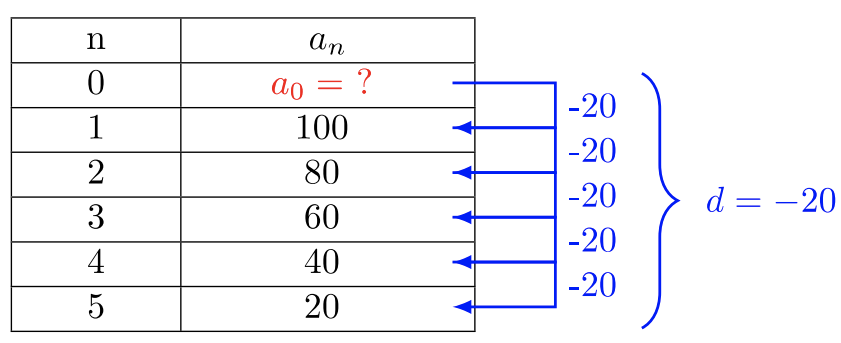
$clipboard_ee68ed069e37b2760f8fc0f27b5a37f04.png$

La diferencia común$d = −20$. Encuentra el valor$a_0$.

$\begin{array} &&a_0 − 20 &= 100 \\ &a_0 − 20 + 20 &= 100 + 20 \\ &a_0 &= 120 \end{array}$

El término general de la secuencia es:

$a_n = −20n + 120$

¡Pruébalo! (Ejercicios)

Para #1 -5, se da el término general de una secuencia.

Enumere los primeros$5$ términos de la secuencia:$a_1, a_2, a_3, a_4, a_5$.
¿La secuencia es aritmética?

$a_n = n^2$
$a_n = 4 − 5n$
$a_n = 2^n$
$a_n = \dfrac{1}{2}n$
$a_n = 0.3n + 1$

Para #6 -9, se da una tabla de valores. Indicar el término general,$a_n$, de la secuencia aritmética.

$n$	$a_n$
\ (n\) ">$1$	\ (a_n\) ">$9$
\ (n\) ">$2$	\ (a_n\) ">$15$
\ (n\) ">$3$	\ (a_n\) ">$21$
\ (n\) ">$4$	\ (a_n\) ">$25$

$n$	$a_n$
\ (n\) ">$1$	\ (a_n\) ">$42$
\ (n\) ">$2$	\ (a_n\) ">$38$
\ (n\) ">$3$	\ (a_n\) ">$34$
\ (n\) ">$4$	\ (a_n\) ">$30$

$n$	$a_n$
\ (n\) ">$1$	\ (a_n\) ">$7$
\ (n\) ">$2$	\ (a_n\) ">$7.25$
\ (n\) ">$3$	\ (a_n\) ">$7.5$
\ (n\) ">$4$	\ (a_n\) ">$7.75$

$n$	$a_n$
\ (n\) ">$1$	\ (a_n\) ">$65.4$
\ (n\) ">$2$	\ (a_n\) ">$52.2$
\ (n\) ">$3$	\ (a_n\) ">$39$
\ (n\) ">$4$	\ (a_n\) ">$25.8$

Para #10 -15, encuentra el término general de la secuencia aritmética. Supongamos que el primer término es$a_1$.

$8, 15, 22, 29, …$
$110, 85, 60, 35, …$
$9, 7.4, 5.8, 4.2, …$
$\dfrac{17}{2} , 8, \dfrac{15}{2} , 7, …$
$−20, −8, 4, 16, 28, …$
$4 \dfrac{1}{2} , 5 \dfrac{1}{4} , 6, 6 \dfrac{3}{4} , …$

Para #16 -20, se describe una secuencia aritmética. Encuentra el término general$a_n$.

La secuencia aritmética tiene diferencia común$d=8$. El primer término$a_1 = 28$.
La secuencia aritmética tiene primer término$a_1 = 40$ y segundo término$a_2 = 36$.
La secuencia aritmética tiene primer término$a_1 = 6$ y tercer término$a_3 = 24$.
La secuencia aritmética tiene diferencia común$d = −2$ y tercer término$a_3 = 15$.
La secuencia aritmética tiene diferencia común$d = 3.6$ y quinto término$a_5 = 10.2$.

Explique cómo la fórmula para el término general dada en esta sección:$a_n = d \cdot n + a_0$ es equivalente a la siguiente fórmula:$a_n = a_1 + d(n − 1)$
Algunas secuencias tienen un número finito de términos. Encuentra el número de términos en la secuencia aritmética finita:$3, 17, 31, … ,143$
Algunas secuencias tienen un número finito de términos. Encuentra el número de términos en la secuencia aritmética finita:$80, 69, 58, … , −52$
Crear una fórmula para encontrar el número de términos una secuencia aritmética finita cuando se les da el primer y el último término de la secuencia. Supongamos que el primer término es$a_1$ y el último término es$a_k$.

\(n\)	\(a_n\)
\ (n\) ">\(1\)	\ (a_n\) ">\(9\)
\ (n\) ">\(2\)	\ (a_n\) ">\(15\)
\ (n\) ">\(3\)	\ (a_n\) ">\(21\)
\ (n\) ">\(4\)	\ (a_n\) ">\(25\)

\(n\)	\(a_n\)
\ (n\) ">\(1\)	\ (a_n\) ">\(42\)
\ (n\) ">\(2\)	\ (a_n\) ">\(38\)
\ (n\) ">\(3\)	\ (a_n\) ">\(34\)
\ (n\) ">\(4\)	\ (a_n\) ">\(30\)

\(n\)	\(a_n\)
\ (n\) ">\(1\)	\ (a_n\) ">\(7\)
\ (n\) ">\(2\)	\ (a_n\) ">\(7.25\)
\ (n\) ">\(3\)	\ (a_n\) ">\(7.5\)
\ (n\) ">\(4\)	\ (a_n\) ">\(7.75\)

\(n\)	\(a_n\)
\ (n\) ">\(1\)	\ (a_n\) ">\(65.4\)
\ (n\) ">\(2\)	\ (a_n\) ">\(52.2\)
\ (n\) ">\(3\)	\ (a_n\) ">\(39\)
\ (n\) ">\(4\)	\ (a_n\) ">\(25.8\)