8.4: Secuencias cuadráticas
- Page ID
- 115920
Las funciones cuadráticas son funciones polinómicas de grado dos. Por ejemplo,\(f(x) = x^2\) es una función cuadrática. Esta sección explorará patrones en funciones y secuencias cuadráticas. Identificar patrones dentro de una tabla de funciones nos da pistas valiosas para construir la función correcta para que coincida con el patrón matemático.
Cómo detectar una secuencia cuadrática:
A diferencia de una secuencia aritmética que tiene una diferencia común\(d = a_n − a_{n-1}\), la secuencia cuadrática no tendrá una diferencia común hasta que se tome la segunda diferencia, ¡o la diferencia de la diferencia!
Considerar la secuencia:\(1, 4, 9, 16, 25, …\) que tiene término general\(a_n = n^2\).
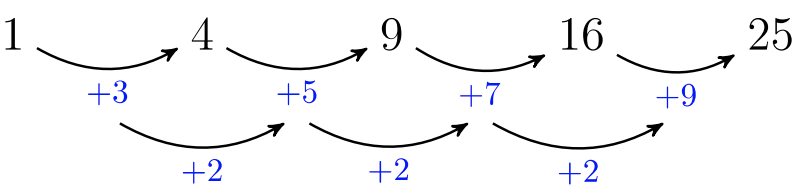
Se tomó la primera diferencia, pero no encontramos una diferencia común. La primera diferencia da los valores poco comunes:\(3, 5, 7, 9\). Sin embargo, persistimos y tomamos una diferencia de las diferencias:\(5 − 3 = 2\),\(7 − 5 = 2\), y\(9 − 7 = 2\). La segunda capa de diferencias reveló un valor común:\(2\). La secuencia es una secuencia cuadrática si la primera diferencia no tiene una diferencia común, ¡pero la segunda diferencia sí!
La secuencia de cuadrados es otra hermosa visual. Además, lo visual realmente justifica por qué llamamos a estos números “cuadrados”.
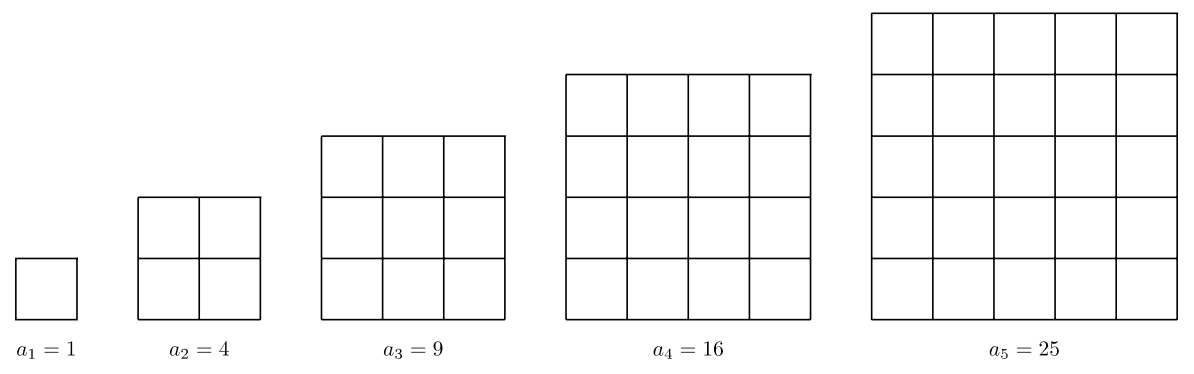
También es notable que la secuencia de cuadrados puede ser creada por la secuencia de sumas parciales de números impares. ¡La maravilla de las matemáticas nos sigue asombrando!
\(\begin{array} &a_1 &= 1 \\ a_2 &= 1 + 3 = 4 \\ a_3 &= 1 + 3 + 5 = 9\\ a_4 &= 1 + 3 + 5 + 7 = 16\\ a_5 &= 1 + 3 + 5 + 7 + 9 = 25 \\ \text{etc.} \end{array}\)
Considera el patrón a continuación. ¿Cuántos azulejos cuadrados pequeños habrá en la\(10^{\text{th}}\) etapa\((a_{10})\) de este patrón?
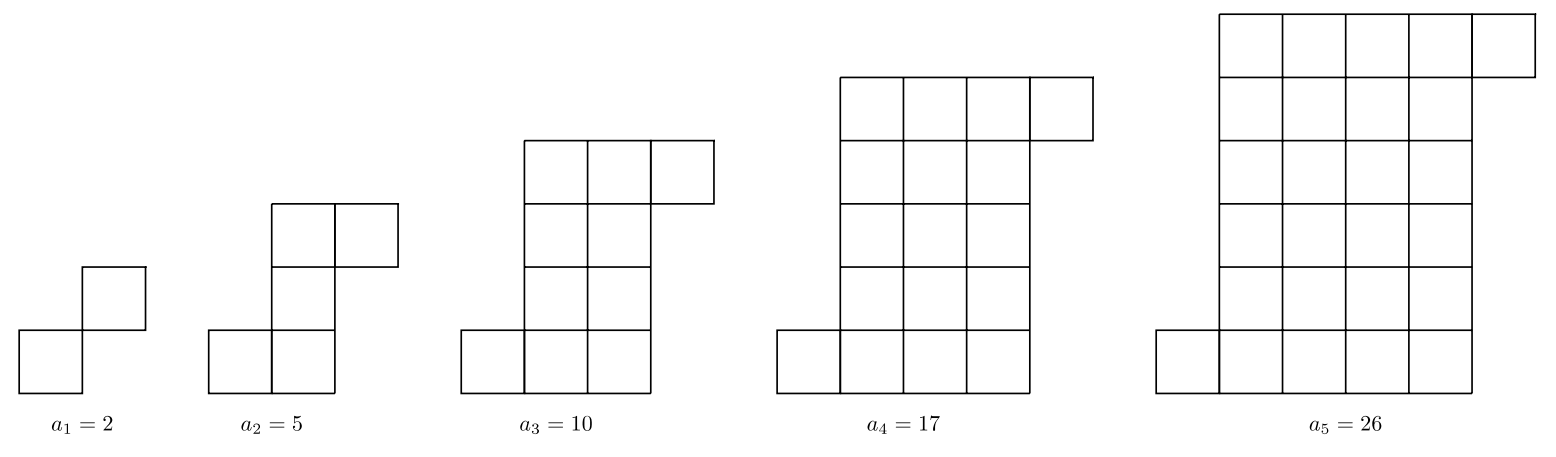
Solución
El patrón es una secuencia cuadrática:
Podemos ver patrones\(2\) separados. Las\(2^{\text{nd}}\),\(3^{\text{rd}}\),\(4^{\text{th}}\), y\(5^{\text{th}}\) las figuras contienen un patrón de cuadrados:\(1, 4, 9, 16, …\) Abajo, los cuadrados son de color amarillo sombreado que crean el Patrón de cuadrados. Las filas superior e inferior crean un patrón lineal (azul), que es una secuencia aritmética.
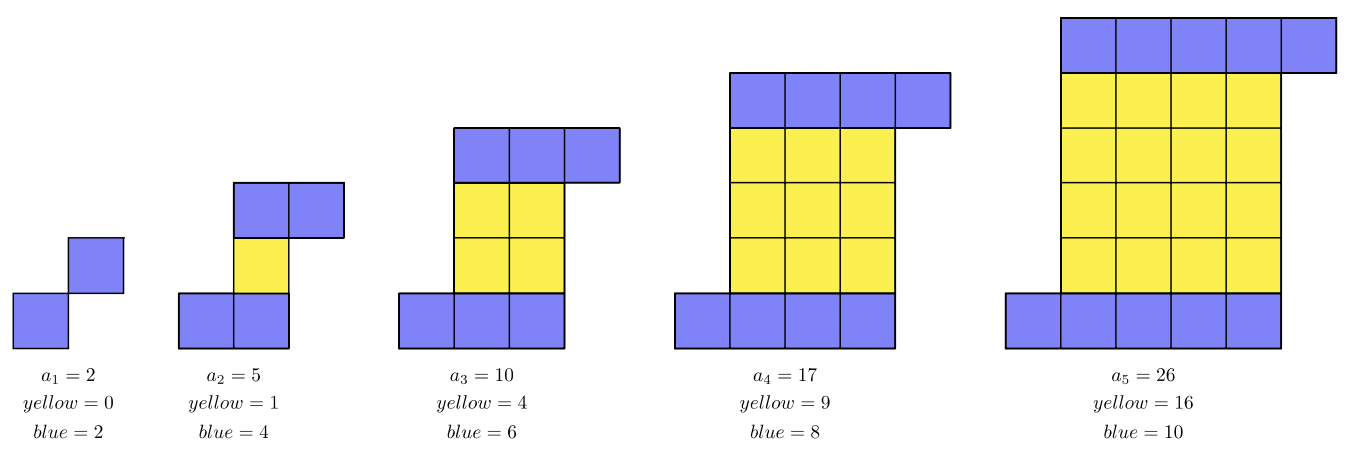
La secuencia azul es la\(2, 4, 6, 8, 10, …\) que tiene término general\(b_n = 2n\)
La secuencia amarilla es la\(0, 1, 4, 9, 16, …\) que tiene término general\(y_n = (n − 1)^2\)
La secuencia azul y amarilla juntas forman la secuencia general de la figura,\(a_n\).
\(\begin{array} &a_n &= b_n + y_n &\text{blue sequence \(+\)secuencia amarilla\(= a_n\)}\\ a_n &= 2n + (n − 1) ^2 &\ text {Sustituir el término general de la secuencia.}\\ a_n &=\ underbrackets {2n} _ {\ text {blue}} +\ underbrackets {n^2-2n+1} _ {\ text {yellow}} &\ text {Expandir, usando FOIL.}\\ a_n &= n^2 + 1 &\ text {Simplificar.} \ end {array}\)
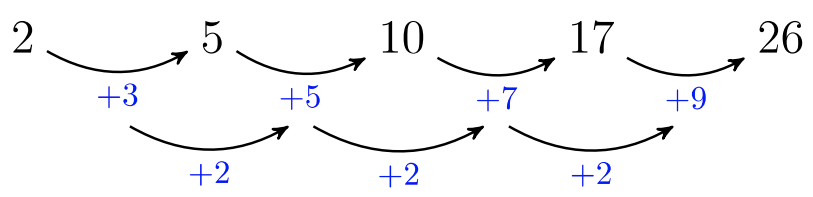
A continuación se muestran\(4\) las primeras etapas de un patrón. ¿Cuántos círculos se requerirán para construir el\(25^{\text{th}}\) escenario\((a_{25})\)?
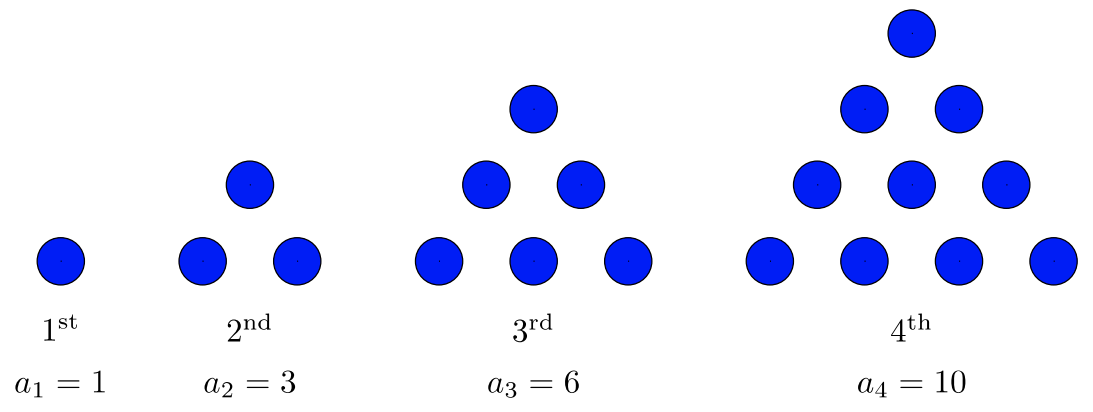
Solución
El número de círculos en cada figura crea una secuencia cuadrática, que podemos ver al encontrar la diferencia común en la segunda diferencia.
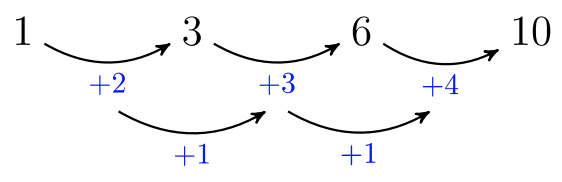
El reto aquí es encontrar el valor\((a_{25})\). Aunque hay muchos enfoques que uno podría tomar, este es un método para encontrar\((a_{25})\).
Observe que la secuencia\(1, 3, 6, 10, …\) es la secuencia de sumas parciales de números consecutivos:
Por lo tanto,\(a_{25} = 1 + 2 + 3 + ⋯ + 25\). En lugar de realizar la suma un término a la vez, escribamos la suma dos veces: uno creciente y otro decreciente, luego agreguemos verticalmente. Sucede algo genial:
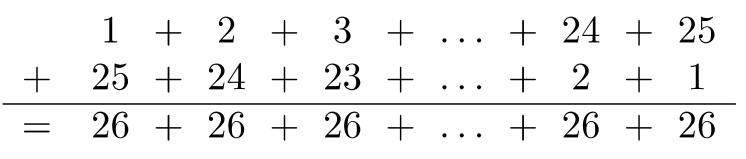
Por lo tanto,
\(\begin{array} &a_{25} + a_{25} &= 25 \cdot 26 \\ 2a_{25} &= 650 \\ \dfrac{2a_{25}}{2} &= \dfrac{650}{2} \\ a_{25} &= 325 \end{array}\)
Sumando Números Consecutivos: 1 a n:
El ejemplo anterior (Ejemplo 8.4.2) demostró un método para encontrar la suma de los primeros números\(25\) consecutivos.
\(1 + 2 + 3 + ⋯ + 25 = \dfrac{25 \cdot 26}{2}\)
Generalicemos el hallazgo\(s_n\), la suma de los primeros números naturales\(n\) consecutivos. Nuevamente, usando el método de Ejemplo\(8.4.2\):
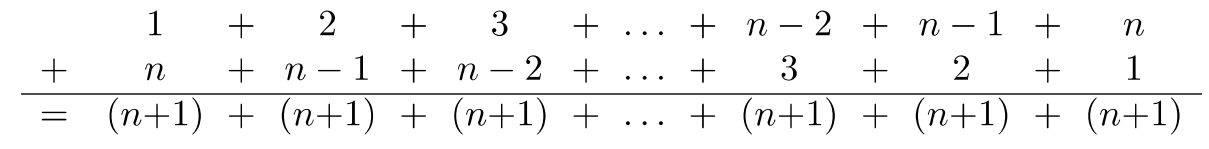
Por lo tanto,
\(\begin{array} & s_n + s_n &= n(n + 1) \\ 2s_n &= n(n + 1) \\ \dfrac{2s_n}{2} &= \dfrac{n(n + 1)}{2} \\ s_n &= \dfrac{n(n + 1)}{2} \end{array}\)
En su primer día de clase, el maestro de Jackson le pide a ese estudiante que se dé la mano y se presente el uno al otro. Hay\(25\) alumnos en la clase. ¿Cuántos apretones de manos diferentes pueden ocurrir durante este rompehielos si cada estudiante le da la mano a todos los demás estudiantes?
Solución
Un paso importante para la resolución de problemas es entender el problema. Empecemos poco a poco. Supongamos que sólo hay\(2\) gente en una clase. Si Chloe le da la mano a Jackson, se ha producido un apretón de manos, ¡y ya está! Ahora agreguemos a otra persona a la sala y consideremos una clase de\(3\) alumnos. Luego agregue otro para un tamaño de clase de\(4\). Luego otro... y crear un gráfico de resultados.
| \(n =\)tamaño de la clase | \(b_n =\)apretones de manos |
|---|---|
| \ (n =\) tamaño de clase">\(2\) | \ (b_n =\) apretones de manos">\(1\) |
| \ (n =\) tamaño de clase">\(3\) | \ (b_n =\) apretones de manos">\(3\) |
| \ (n =\) tamaño de clase">\(4\) | \ (b_n =\) apretones de manos">\(6\) |
| \ (n =\) tamaño de clase">\(5\) | \ (b_n =\) apretones de manos">\(10\) |
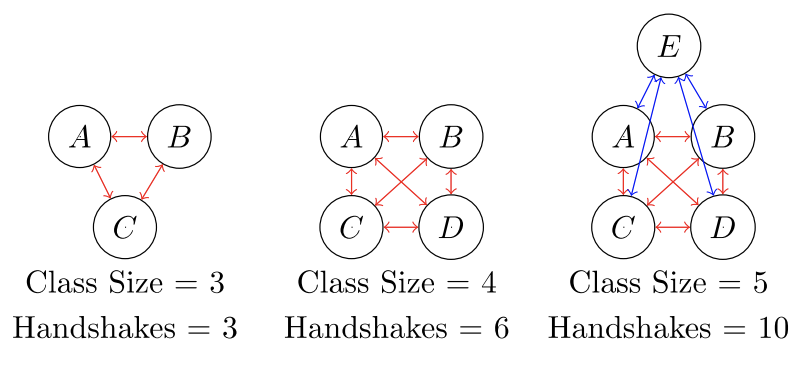
Un patrón emerge muy parecido al ejemplo anterior (Ejemplo 8.4.2). Sin embargo, los\(n\) -valores (tamaño de clase) son uno más que los\(n\) -valores (el número de figura) en el Ejemplo 8.4.2. Podemos ajustarnos fácilmente por la diferencia. Compara las tablas entre los dos ejemplos y ajusta en consecuencia
| De Ejemplo\(8.4.2\) | |
|---|---|
| \ (8.4.2\) "> número de\(n =\) figura | \(a_n =\)# de círculos |
| \ (8.4.2\) ">\(1\) | \(1\) |
| \ (8.4.2\) ">\(2\) | \(3\) |
| \ (8.4.2\) ">\(3\) | \(6\) |
| \ (8.4.2\) ">\(4\) | \(10\) |
| \ (8.4.2\) ">\(n\) | \(\dfrac{n(n+1)}{2}\) |
Utilice el Ejemplo 8.4.2 como modelo para encontrar la fórmula del Ejemplo 8.4.3. El\(n\)-values of Example 8.4.2 are one less than the \(n\)-values of Example 8.4.3.
| De Ejemplo\(8.4.3\) | |
|---|---|
| \ (8.4.3\) "> tamaño\(n =\) de clase | \(b_n =\)apretones de manos |
| \ (8.4.3\) ">\(2\) | \(1\) |
| \ (8.4.3\) ">\(3\) | \(3\) |
| \ (8.4.3\) ">\(4\) | \(6\) |
| \ (8.4.3\) ">\(5\) | \(10\) |
| \ (8.4.3\) ">\(n\) | ¿Fórmula? |
Como conocemos la fórmula del Ejemplo 8.4.2, ajustemos los\(n\) −valores de Ejemplo\(8.4.3\) para que coincidan con el Ejemplo 8.4.2. Como estamos haciendo coincidir el Ejemplo 8.4.3 con el Ejemplo 8.4.2, necesitamos restar uno del\(n\) valor -. En esencia, el valor\(b_n\) del Ejemplo 8.4.3 (apretones de manos) coincide con el valor de\(a_{n-1}\) para el Ejemplo 8.4.2 (número de círculos).
\(b_{25}\)del Ejemplo 8.4.3 es el mismo que el\(a_{24}\) del Ejemplo 8.4.2.
Una habilidad importante para la resolución de problemas es utilizar un trabajo que ya se ha logrado. No todos los problemas son una pizarra nueva.
\(\begin{array}& a_{24} &= \dfrac{24(24+1)}{2} &\text{Substitute \(n = 24\)en la fórmula del Ejemplo 8.4.2.}\\ a_ {24} &=\ dfrac {24 (25)} {2} &\ text {Simplifica primero los paréntesis.}\\ a_ {24} &=\ dfrac {600} {2} &\ text {Simplifica el numerador. Entonces divide.}\\ a_ {24} &= 300 &\ text {Pero ahora aplica esta respuesta al Ejemplo 8.4.3:\(b_{25} = 300\).} \ end {array}\)
Para encontrar la fórmula,\(a_n\), para el Ejemplo 8.4.3, sustituya\((n − 1)\)\(n\) en el Ejemplo 8.4.2.
Fórmula para el Ejemplo 8.4.3:
\(\begin{array} && \dfrac{(\textcolor{red}{n−1})[(\textcolor{red}{n−1})+1]}{2} &\text{Replace each \(n\)con\((n − 1)\) en la fórmula del Ejemplo 8.4.2.}\\ &\ dfrac {(n−1) n} {2} &\ text {Simplificar entre paréntesis.}\\ &\ dfrac {n (n−1)} {2} &\ text {Esta es la fórmula del Ejemplo 8.4.3.}\\ &b_ {25} =\ dfrac {25 (24)} {2} &\ text {Verifica que obtengamos la misma respuesta,\(300\), como arriba.}\ \ &b_ {25} = 300 &\ end {array}\)
Respuesta En la clase de\(25\) alumnos de Jerome, habría\(300\) diferentes apretones de manos si cada alumno estrechara la mano de cada uno de los demás estudiantes.
¡Pruébalo! (Ejercicios)
Para #1 -3, se da el término general de la secuencia.
a. Indicar los cinco primeros términos, empezando por\(n = 1\).
b. Encuentra el valor\(a_{12}\).
- \(a_n = n^2 + n − 1\)
- \(a_n = 2(n + 1) 2\)
- \(a_n = 2n^2 + 2\)
Para #4 -8, Vamos\(s_n =\) La suma de los primeros números naturales\(n\) consecutivos. Encuentra el valor indicado.
- \(s_{32}\)
- \(s_{80}\)
- \(s_{100}\)
- \(s_{201}\)
- \(s_{496}\)
Para #9 -13, Una habitación cuenta con\(n\) personas, todas las cuales estrecharán la mano una vez con cada otra persona en la habitación. Dejar\(b_n =\) número de diferentes apretones de manos. Encuentra el valor indicado.
- \(b_{16}\)
- \(b_{36}\)
- \(b_{52}\)
- \(b_{100}\)
- \(b_{229}\)
- Encuentra la suma de los primeros números\(30\) impares.
- Usa el hecho de que\(2 + 4 + 6 + 8 + ⋯ = 2(1 + 2 + 3 + 4 + ⋯ )\) para encontrar la suma de los primeros números\(50\) pares.
- Escribe una fórmula para describir la suma del primer\(n\) número de números pares.
Para #17 -21, A continuación se muestra un patrón de figuras. Deje que\(a_n =\) el número de pequeños azulejos cuadrados utilizados para crear la figura\(n\). Encuentra el valor indicado.
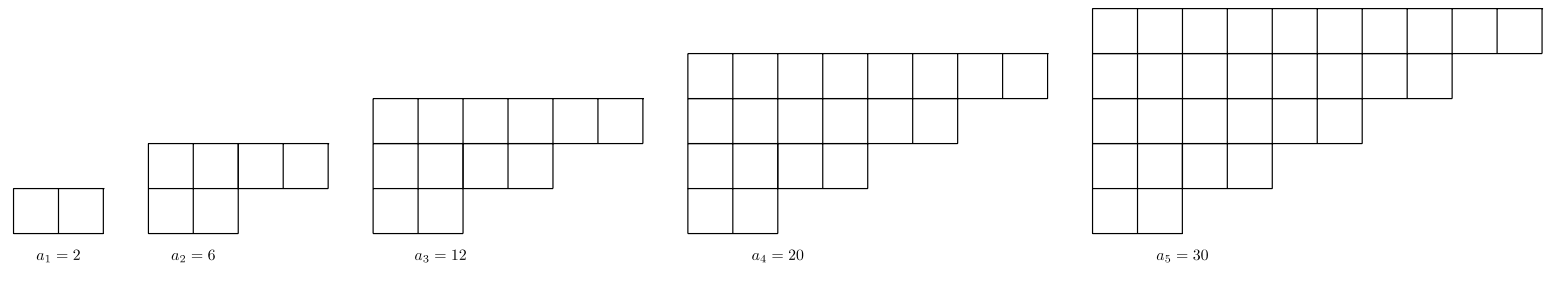
- \(a_{6}\)
- \(a_{8}\)
- \(a_{22}\)
- \(a_{60}\)
- La fórmula\(a_n\).
Para #22 -24, primero determine el número de cerillas en cada Figura 1-4. Deja que\(a_n =\) el número de cerillas en la figura\(n\). Encuentra el valor indicado.
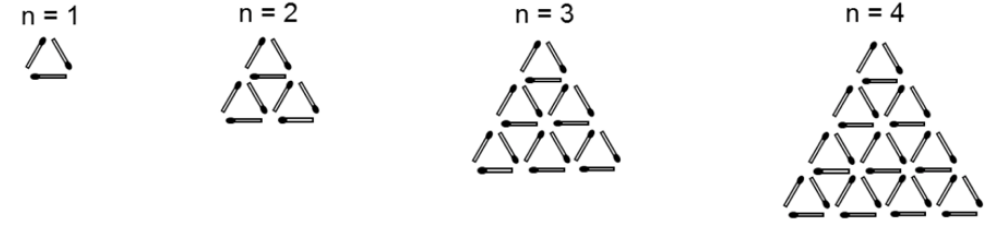
- \(a_5\)
- Encontrar\(a_n\) dado eso\(a_n = \dfrac{3n(n+k)}{2}\) para algunos\(k\).
- \(a_{45}\)
Para #25 -27, los\(4\) polígonos a continuación demuestran cómo contar las diagonales dentro de cada polígono. Una diagonal (mostrada en azul) es la conexión de vértices no vecinos. Deje que\(p_n =\) el número de diagonales en cualquier figura\(n\) −sided. Encuentra el valor indicado.
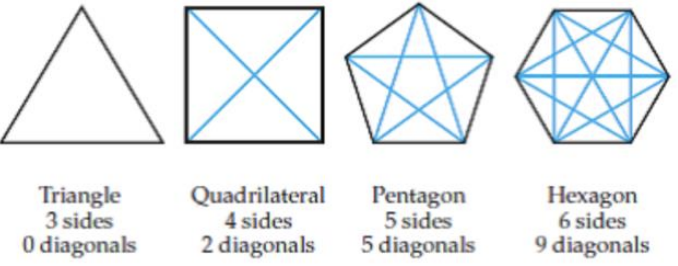
- \(p_7\)
- Dado que\(p_n = \dfrac{n(n−k)}{2}\) para algunos\(k\), Encuentra\(k\) y\(p_n\).
- \(p_{40}\)
Para #28 -30, refiérase al experimento con gravedad que se describe a continuación:
Tienes curiosidad si existe una relación entre el número de pies que cae una pelota desde un balcón\(144\) pies sobre el suelo. Se configura una cámara para tomar una ráfaga de fotografías cada segundo mientras una pelota cae frente a una tabla de alturas. Se crea la siguiente tabla a partir de las fotografías:
| Tiempo (seg) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|
| Distancia (pies) | \(0\) | \(16\) | \(64\) | \(144\) |
- Razón que la distancia del balón es una secuencia cuadrática. ¿Cómo lo sabías?
- Después de graficar los puntos, razonas que la secuencia tiene término general\(d_t = kt^2\) donde el\(t =\) tiempo en segundos y\(k\) es un número real. Determinar el valor de\(k\), luego encontrar\(d_t\).
- Usando tus respuestas a #28 y #29, supongamos que estabas parado en lo alto de un acantilado para el que no conocías la altura. Se te cayó una roca desde arriba. \(6\)segundos después, escuchaste que la roca golpeaba el suelo. ¿Qué tan alto del suelo estás?
Para #31 -33, use la tabla para describir la elevación de los aviones:
Para un área de ala dada, el levantamiento de un avión es proporcional al cuadrado de su velocidad.
Deja que la\(s =\) velocidad del avión. Entonces\(l_s = ks^2\) para alguna constante,\(k\).
En la siguiente tabla se muestra el levantamiento de un avión Boeing 737 a diversas velocidades.
| Velocidad (mph) | \(0\) | \(75\) | \(150\) | \(225\) | \(300\) | \(375\) |
|---|---|---|---|---|---|---|
| Elevación (\(1000\)s de libra) | \(0\) | \(25\) | \(100\) | \(225\) | \(400\) | \(625\) |
- Usted razona que el levantamiento de un avión es una secuencia cuadrática. ¿Cómo lo sabías?
- Después de graficar los puntos, razonas que la secuencia tiene término general\(l_s = ks^2\) donde la\(s =\) velocidad en mph y\(k\) es una constante. Determinar el valor de\(k\), luego encontrar\(l_s\).
- Usa tus respuestas a #31 y #32 para encontrar el ascensor para un avión que viaja\(425\) mph.


