1.6: Gráficas de Funciones
- Page ID
- 119449
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la Sección 1.3 definimos una función como un tipo especial de relación; una en la que cada coordenada x se emparejó con una sola coordenada y. Pasamos la mayor parte del tiempo en esa sección mirando las funciones gráficamente porque eran, después de todo, solo conjuntos de puntos en el plano. Luego en la Sección 1.4 describimos una función como un proceso y definimos la notación necesaria para trabajar con funciones algebraicamente. Entonces ahora es el momento de volver a mirar las funciones gráficamente, solo que esta vez lo haremos con la notación definida en la Sección 1.4. Empezamos con lo que no debería ser una conexión sorprendente.
La gráfica de una función\(\ f\) es el conjunto de puntos que satisfacen la ecuación\(\ y = f(x)\). Es decir, el punto\(\ (x, y)\) está en la gráfica de\(\ f\) si y sólo si\(\ y = f(x)\).
Gráfica\(\ f(x)=x^{2}-x-6\).
Solución
Para graficar\(\ f\), graficamos la ecuación\(\ y = f(x)\). Para ello, utilizamos las técnicas señaladas en la Sección 1.2.1. Específicamente, verificamos si hay intercepciones, probamos simetría y trazamos puntos adicionales según sea necesario. Para encontrar las intercepciones x, nos fijamos\(\ y = 0\). Ya que\(\ y = f(x)\), esto significa\(\ f(x) = 0\).
\ (\\ begin {alineado}
f (x) &=x^ {2} -x-6\\
0 &=x^ {2} -x-6\\
0 & =( x-3) (x+2)\ quad\ quad\ quad\ text {factor}\\
x-3=0 &\ text {o} x+2=0\\
x &=-2,3
\ end {alineado}\)
Entonces obtenemos (−2, 0) y (3, 0) como x-intercepta. Para encontrar la intercepción y, nos fijamos\(\ x = 0\). Usando la notación de funciones, esto es lo mismo que encontrar\(\ f(0)\) y\(\ f(0)=0^{2}-0-6=-6\). Así, la intercepción y es (0, −6). En lo que respecta a la simetría, podemos decir por las intercepciones que la gráfica no posee ninguna de las tres simetrías discutidas hasta el momento. (Debe verificar esto.) Podemos hacer una tabla análoga a las que hicimos en la Sección 1.2.1, trazar los puntos y conectar los puntos de una manera algo agradable para obtener la gráfica de abajo a la derecha.
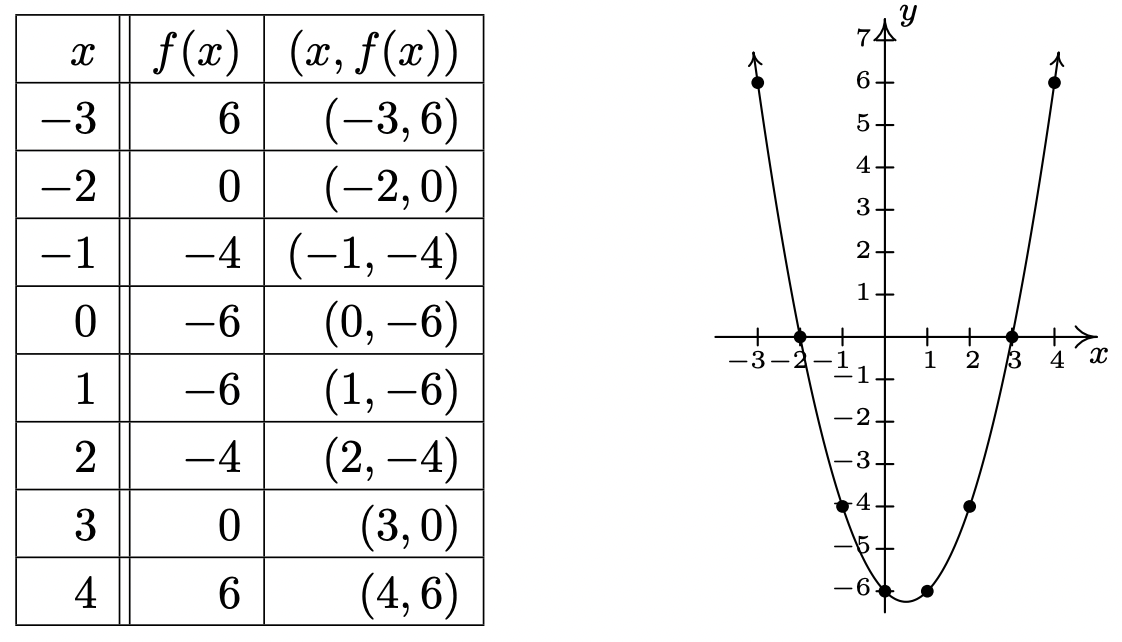
Graficar funciones definidas poco a poco es un desafío un poco más difícil.
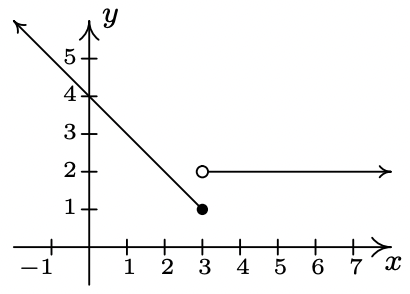
Gráfico:\ (\ f (x) =\ left\ {\ begin {array} {lll}
4-x^ {2} &\ text {if} & x<1\\
x-3, &\ text {if} & x\ geq 1
\ end {array}\ right.\)
Solución
Procedemos como antes, encontrando intercepciones, probando simetría y luego trazando puntos adicionales según sea necesario. Para encontrar las intercepciones x, como antes, establecemos\(\ f(x) = 0\). El giro es que tenemos dos fórmulas para\(\ f(x)\). Para\(\ x < 1\), utilizamos la fórmula\(\ f(x)=4-x^{2}\). Ajuste\(\ f(x) = 0\) da\(\ 0=4-x^{2}\), así que eso\(\ x=\pm 2\). No obstante, de estas dos respuestas, sólo\(\ x = −2\) cabe en el dominio\(\ x < 1\) para esta pieza. Esto significa que la única intercepción x para la\(\ x < 1\) región del eje x es (−2, 0). Para\(\ x ≥ 1\),\(\ f(x) = x − 3\). Ajuste\(\ f(x) = 0\) da\(\ 0 = x − 3\), o\(\ x = 3\). Ya que\(\ x = 3\) satisface la desigualdad\(\ x ≥ 1\), obtenemos (3, 0) como otra intercepción x. A continuación, buscamos la intercepción y. Observe que\(\ x = 0\) cae en el dominio\(\ x < 1\). Así se\(\ f(0)=4-0^{2}=4\) obtiene la intercepción y (0, 4). En lo que respecta a la simetría, se puede comprobar que la ecuación\(\ y=4-x^{2}\) es simétrica alrededor del eje y; desafortunadamente, esta ecuación (y su simetría) es válida solo para\(\ x < 1\). También se puede verificar que no\(\ y = x−3\) posee ninguna de las simetrías discutidas en la Sección 1.2.1. Al trazar puntos adicionales, es importante tener en cuenta las restricciones\(\ x\) para cada pieza de la función. El punto de inflexión para esta función es\(\ x = 1\), ya que aquí es donde cambian las ecuaciones. Cuando\(\ x = 1\), usamos la fórmula\(\ f(x) = x − 3\), entonces el punto en la gráfica\(\ (1, f(1))\) es\(\ (1, −2)\). Sin embargo, para todos los valores menores a 1, usamos la fórmula\(\ f(x)=4-x^{2}\). Como ya hemos comentado anteriormente en la Sección 1.2, no existe un número real que preceda inmediatamente\(\ x = 1\) en la línea numérica. Así, para los valores\(\ x = 0.9\)\(\ x = 0.99\),\(\ x = 0.999\), y así sucesivamente, encontramos los valores y correspondientes usando la fórmula\(\ f(x)=4-x^{2}\). Haciendo una mesa como antes, vemos que a medida que los\(\ x\) valores se acercan sigilosamente de esta\(\ x = 1\) manera, los\(\ f(x)\) valores se acercan cada vez más a 1 a\(\ 4-1^{2}=3\). Para indicarlo gráficamente, utilizamos un círculo abierto en el punto (1, 3). Al juntar toda esta información y trazar puntos adicionales, obtenemos
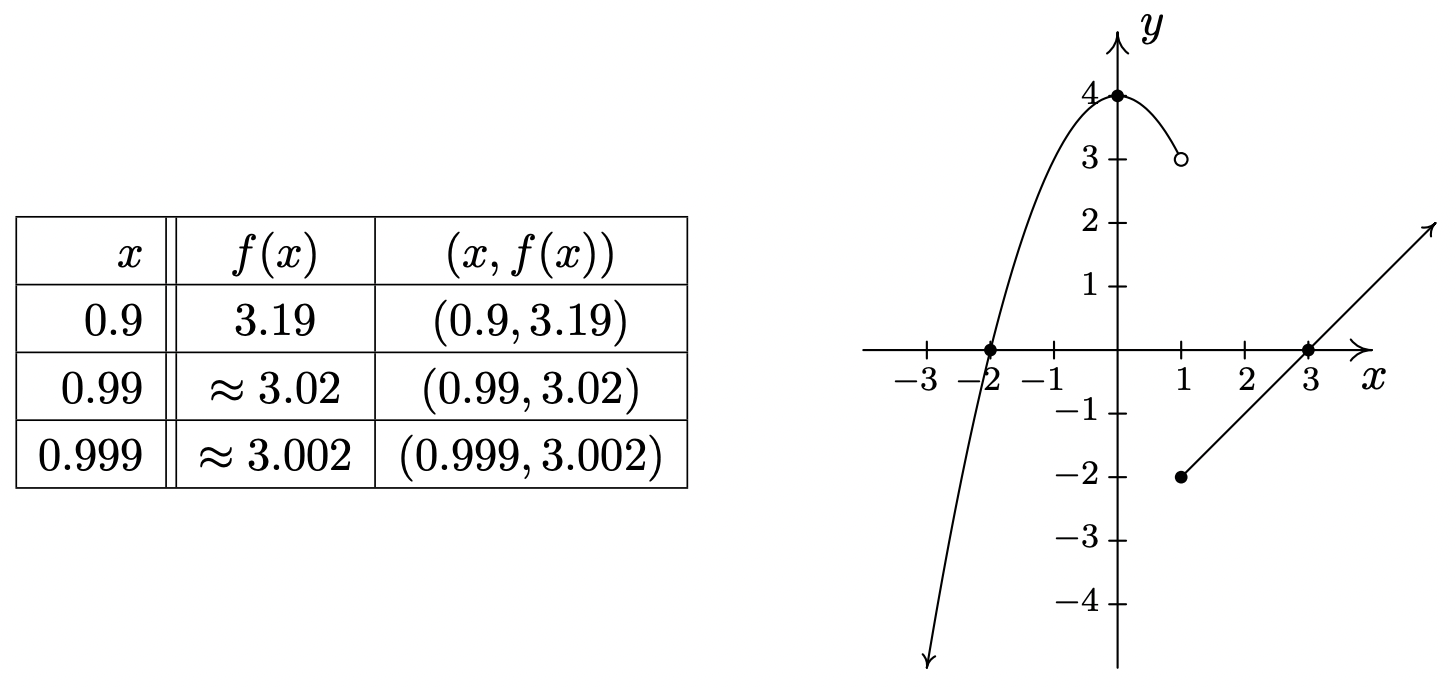
En los dos ejemplos anteriores, se\(\ y = f(x)\) encontraron las coordenadas x de las intercepciones x de la gráfica de resolviendo\(\ f(x) = 0\). Por ello, se les llama los ceros de\(\ f\).
Los ceros de una función\(\ f\) son las soluciones a la ecuación\(\ f(x) = 0\). En otras palabras,\(\ x\) es un cero de\(\ f\) si y solo si\(\ (x, 0)\) es una intercepción x de la gráfica de\(\ y = f(x)\).
De las tres simetrías discutidas en la Sección 1.2.1, solo dos son de importancia para las funciones: simetría alrededor del eje y y simetría sobre el origen. 2 Recordemos que podemos probar si la gráfica de una ecuación es simétrica alrededor del eje\(\ −x\) y\(\ x\) reemplazando por y verificando para ver si resulta una ecuación equivalente. Si estamos graficando la ecuación\(\ y = f(x)\), sustituyendo\(\ −x\) los\(\ x\) resultados en la ecuación\(\ y = f(−x)\). Para que esta ecuación sea equivalente a la ecuación original\(\ y = f(x)\) que necesitamos\(\ f(−x) = f(x)\). De manera similar, recordamos que para probar la simetría gráfica de una ecuación sobre el origen, reemplazamos x e y con\(\ −x\) y\(\ −y\), respectivamente. Hacer esta sustitución en la ecuación\(\ y = f(x)\) da como resultado\(\ −y = f(−x)\). Resolviendo esta última ecuación para\(\ y\) da\(\ y = −f(−x)\). Para que esta ecuación sea equivalente a la ecuación original\(\ y = f(x)\) necesitamos\(\ −f(−x) = f(x)\), o, de manera equivalente,\(\ f(−x) = −f(x)\). Estos resultados se resumen a continuación.
La gráfica de una función\(\ f\) es simétrica
- sobre el eje y si y solo si\(\ f(−x) = f(x)\) para todos\(\ x\) en el dominio de\(\ f\).
- sobre el origen si y sólo si\(\ f(−x) = −f(x)\) para todos\(\ x\) en el dominio de\(\ f\).
Por razones que no quedarán claras hasta que estudiemos polinomios, llamamos a una función aunque su gráfica sea simétrica sobre el eje y o impar si su gráfica es simétrica sobre el origen. Aparte de una familia muy especializada de funciones que son a la vez pares e impares, 3 funciones se agrupan en una de tres categorías distintas: par, impar, o ni par ni impar.
Determine analíticamente si las siguientes funciones son pares, impares o ni pares ni impares. Verifica tu resultado con una calculadora gráfica.
- \(\ f(x)=\frac{5}{2-x^{2}}\)
- \(\ g(x)=\frac{5 x}{2-x^{2}}\)
- \(\ h(x)=\frac{5 x}{2-x^{3}}\)
- \(\ i(x)=\frac{5 x}{2 x-x^{3}}\)
- \(\ j(x)=x^{2}-\frac{x}{100}-1\)
- \ (\ p (x) =\ left\ {\ begin {array} {rll}
x+3 &\ text {if} & x<0\\
-x+3, &\ text {if} & x\ geq 0
\ end {array}\ right.\)
Solución
El primer paso en todos estos problemas es reemplazar\(\ x\)\(\ −x\) y simplificar.
-
\ (\\ begin {alineado}
f (x) &=\ frac {5} {2-x^ {2}}\\
f (-x) &=\ frac {5} {2- (-x) ^ {2}}\\
f (-x) &=\ frac {5} {2-x^ {2}}\\
f (-x) &=f (x)
\ fin {alineado}\)De ahí,\(\ f\) es parejo. La calculadora gráfica proporciona lo siguiente.
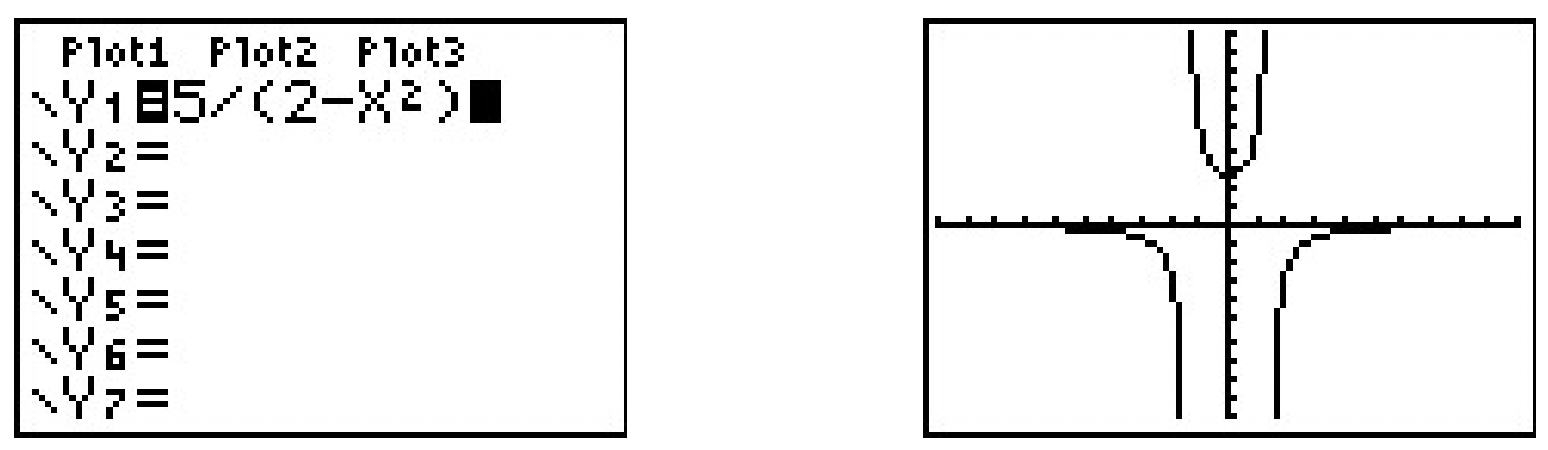
Esto sugiere 4 que la gráfica de\(\ f\) es simétrica alrededor del eje y, como se esperaba.
-
\ (\\ begin {alineado}
g (x) &=\ frac {5 x} {2-x^ {2}}\\
g (-x) &=\ frac {5 (-x)} {2- (-x) ^ {2}}\\
g (-x) &=\ frac {-5 x} {2-x^ {2}}
\ end {alineado}\)No parece que\(\ g(−x)\) sea equivalente a\(\ g(x)\). Para probarlo, comprobamos con un\(\ x\) valor. Después de algún ensayo y error, vemos que\(\ g(1) = 5\) mientras\(\ g(−1) = −5\). Esto prueba que no\(\ g\) es par, pero no descarta la posibilidad que\(\ g\) sea extraña. (¿Por qué no?) Para verificar si\(\ g\) es impar, comparamos\(\ g(−x)\) con\(\ −g(x)\)
\ (\\ comenzar {alineado}
-g (x) &=-\ frac {5 x} {2-x^ {2}}\\
&=\ frac {-5 x} {2-x^ {2}}\\
-g (x) &=g (-x)
\ final {alineado}\)De ahí,\(\ g\) es impar. Gráficamente
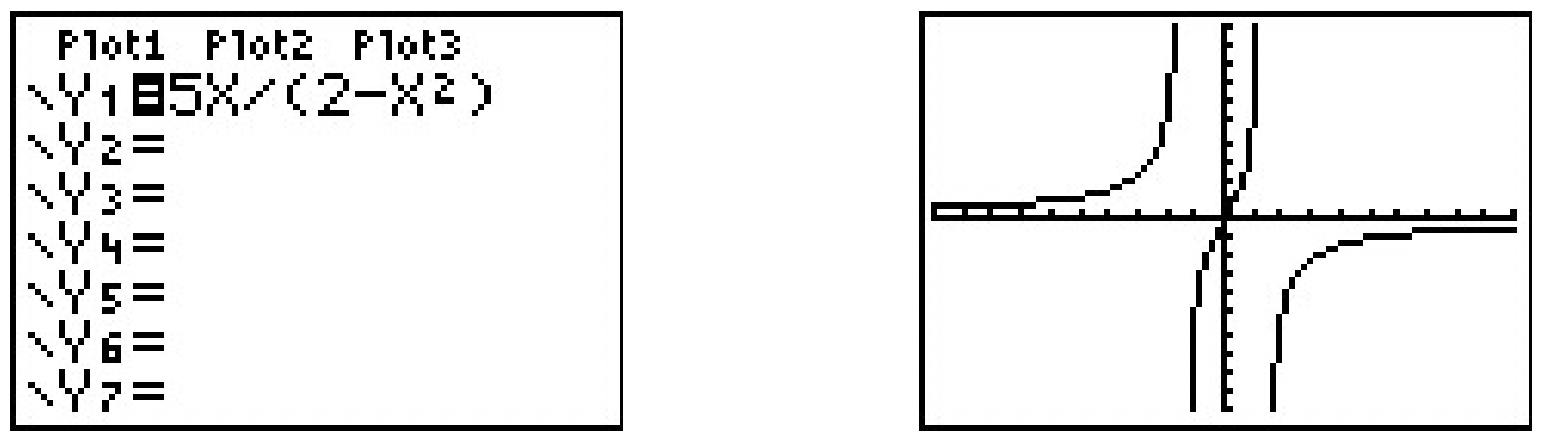
La calculadora indica que la gráfica de\(\ g\) es simétrica sobre el origen, como se esperaba.
-
\ (\\ begin {alineado}
h (x) &=\ frac {5 x} {2-x^ {3}}\\
h (-x) &=\ frac {5 (-x)} {2- (-x) ^ {3}}\\
h (-x) &=\ frac {-5 x} {2+x^ {3}}
\ end {alineado}\)Una vez más,\(\ h(−x)\) no parece ser equivalente a\(\ h(x)\). Comprobamos con un\(\ x\) valor, por ejemplo,\(\ h(1) = 5\) pero\(\ h(-1)=-\frac{5}{3}\). Esto demuestra que no\(\ h\) es par y además muestra que no\(\ h\) es extraño. (¿Por qué?) Gráficamente
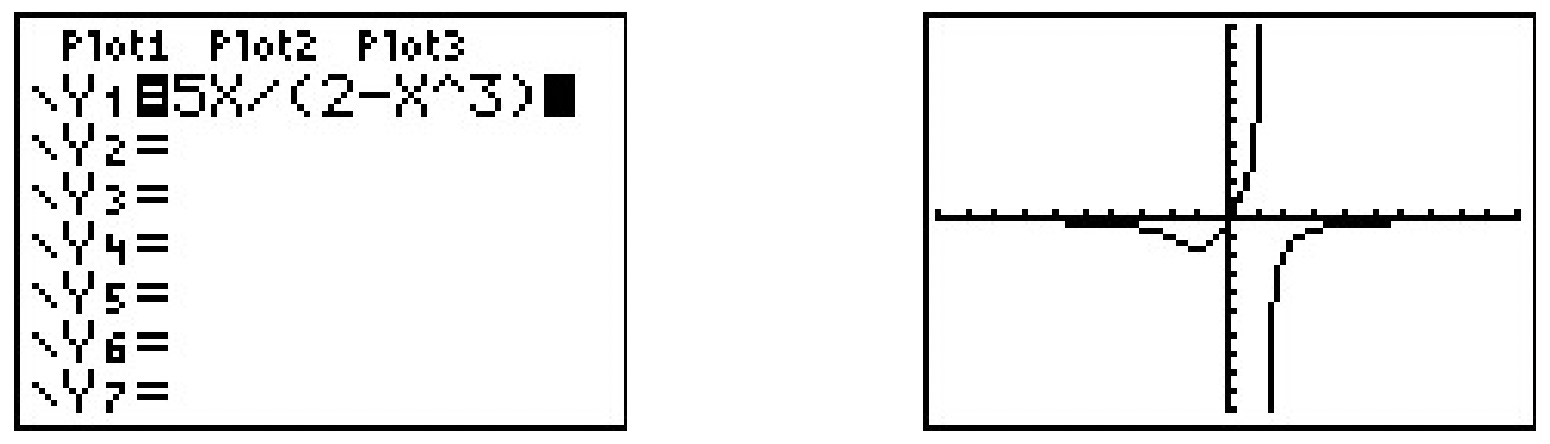
La gráfica de\(\ h\) parece no ser simétrica alrededor del eje y ni del origen.
-
\ (\\ begin {alineado}
i (x) &=\ frac {5 x} {2 x-x^ {3}}\\
i (-x) &=\ frac {5 (-x)} {2 (-x) - (-x) ^ {3}}\\
i (-x) &=\ frac {-5 x} {-2 x+x^ {3}}
\ fin alineado}\)La expresión\(\ i(−x)\) no parece ser equivalente a\(\ i(x)\). No obstante, después de verificar algunos valores de x, por ejemplo\(\ x = 1\) rendimientos\(\ i(1) = 5\) y\(\ i(−1) = 5\), parece que\(\ i(−x)\) hace, de hecho, igual\(\ i(x)\). Sin embargo, si bien esto sugiere que\(\ i\) es parejo, no lo prueba. (Lo hace, sin embargo, probar que no\(\ i\) es extraño.) Para probarlo\(\ i(−x) = i(x)\), necesitamos manipular nuestras expresiones para\(\ i(x)\) y\(\ i(−x)\) y demostrar que son equivalentes. Una pista de cómo proceder está en los numeradores: en la fórmula para\(\ i(x)\), el numerador es\(\ 5x\) y en\(\ i(−x)\) el numerador está\(\ −5x\). Para reescribir\(\ i(x)\) con un numerador de\(\ −5x\), necesitamos multiplicar su numerador por −1. Para mantener igual el valor de la fracción, también necesitamos multiplicar el denominador por −1. Así
\ (\\ begin {alineado}
i (x) &=\ frac {5 x} {2 x-x^ {3}}\\
&=\ frac {(-1) 5 x} {(-1)\ izquierda (2 x-x^ {3}\ derecha)}\\
&=\ frac {-5 x} {-2 x+x^ {3}}
\ end {alineado}\)De ahí,\(\ i(x) = i(−x)\), así\(\ i\) es parejo. La calculadora respalda nuestra conclusión.
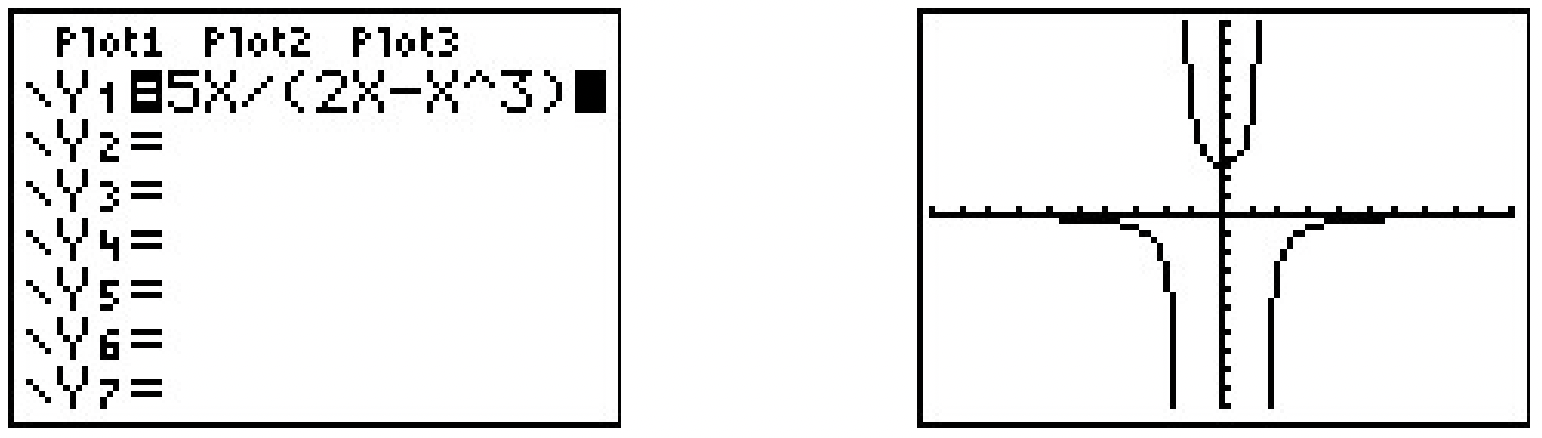
-
\ (\\ begin {alineado}
j (x) &=x^ {2} -\ frac {x} {100} -1\\
j (-x) & =( -x) ^ {2} -\ frac {-x} {100} -1\\
j (-x) &=x^ {2} +\ frac {x} {100} -1
\ end {alineado}\)La expresión for\(\ j(−x)\) no parece ser equivalente a\(\ j(x)\), así que comprobamos usando\(\ x = 1\) para obtener\(\ j(1)=-\frac{1}{100}\) y\(\ j(-1)=\frac{1}{100}\). Esto descarta\(\ j\) estar parejo. No obstante, no descarta\(\ j\) ser extraño. Examinando\(\ −j(x)\) da
\ (\\ comenzar {alineado}
j (x) &=x^ {2} -\ frac {x} {100} -1\\
-j (x) &=-\ izquierda (x^ {2} -\ frac {x} {100} -1\ derecha)\\
-j (x) &=-x^ {2} +\ frac {x} {100} +1
\ end {alineado}\)La expresión\(\ −j(x)\)\(\ j(−x)\) tampoco parece coincidir. Las pruebas\(\ x = 2\) dan\(\ j(2)=\frac{149}{50}\) y\(\ j(-2)=\frac{151}{50}\), así no\(\ j\) es extraño, tampoco. La calculadora da:
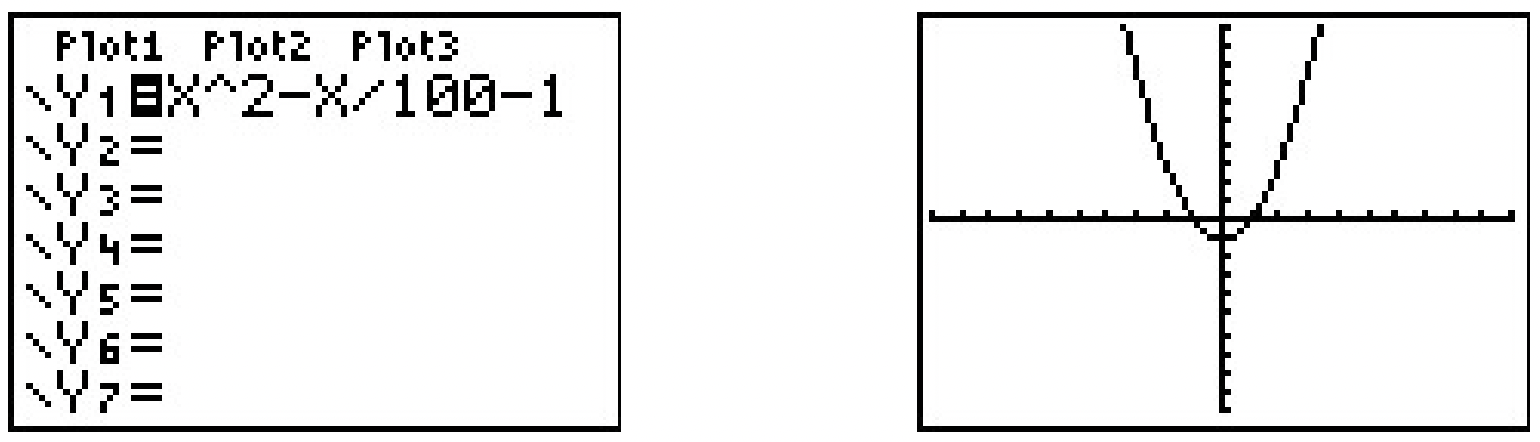
La calculadora sugiere que la gráfica de\(\ j\) es simétrica alrededor del eje y lo que implicaría que\(\ j\) es par. No obstante, hemos demostrado que ese no es el caso.
- Prueba de la gráfica de\(\ y = p(x)\) simetría se complica por el hecho de que\(\ p(x)\) es una función definida por partes. Como siempre, manejamos esto comprobando la condición de simetría verificándola en cada pieza del dominio. Primero consideramos el caso cuando\(\ x < 0\) y nos pusimos a encontrar la expresión correcta para\(\ p(−x)\). Aunque\(\ p(x) = x+ 3\) para\(\ x < 0\),\(\ p(-x) \neq-x+3\) aquí. La razón de esto es que ya\(\ −x > 0\) que\(\ x < 0\), lo que significa encontrar\(\ p(−x)\), necesitamos usar la otra fórmula para\(\ p(x)\), a saber\(\ p(x) = −x+3\). De ahí, para\(\ x < 0\),\(\ p(−x) = −(−x)+3 = x + 3 = p(x)\). Para\(\ x ≥ 0\),\(\ p(x) = −x + 3\) y tenemos dos casos. Si\(\ x > 0\), entonces\(\ −x < 0\) así\(\ p(−x) = (−x) + 3 = −x + 3 = p(x)\). Si\(\ x = 0\), entonces\(\ p(0) = 3 = p(−0)\). De ahí que en todos los casos,\(\ p(−x) = p(x)\), así\(\ p\) es parejo. Desde\(\ p(0) = 3\) pero\(\ p(-0)=p(0)=3 \neq-3\), también tenemos no\(\ p\) es extraño. Si bien graficar no\(\ y = p(x)\) es oneroso de hacer a mano, es instructivo ver cómo ingresar esto en nuestra calculadora. Al usar algunos de los comandos lógicos, 5 tenemos:
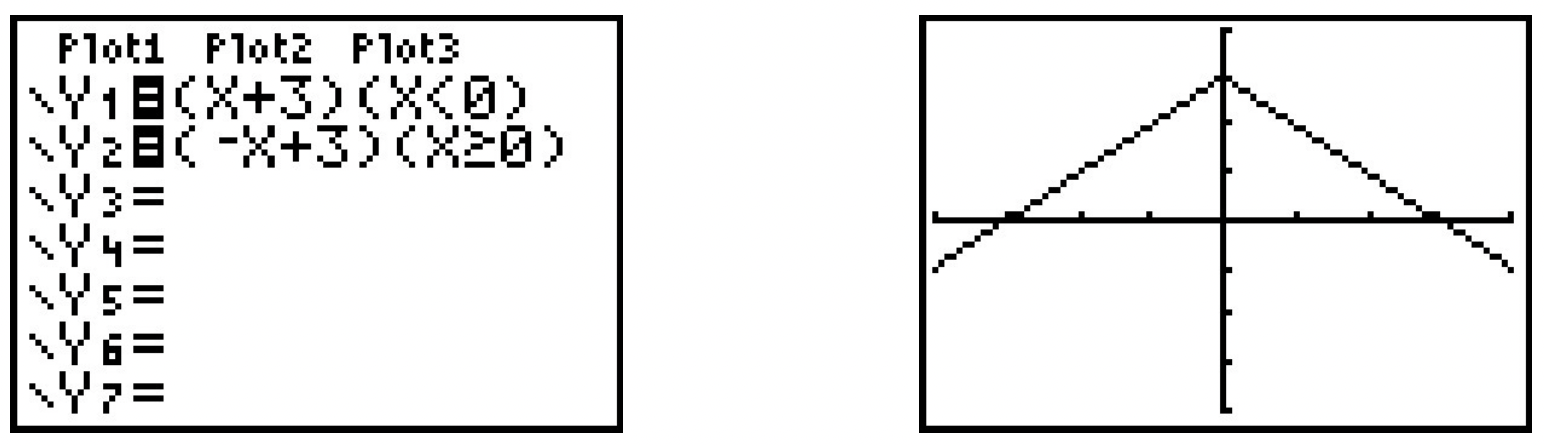
Los osos de la calculadora muestran que la gráfica parece ser simétrica alrededor del eje y.
Hay dos lecciones por aprender del último ejemplo. La primera es que muestrear valores de función en valores x particulares no es suficiente para probar que una función es par o impar − a pesar de que\(\ j(−1) = −j(1)\), j resultó no ser impar. En segundo lugar, si bien la calculadora puede sugerir verdades matemáticas, es el Álgebra el que prueba las verdades matemáticas. 6
El último tema que queremos abordar en esta sección es el comportamiento general de la función. Como verás en los siguientes capítulos, cada familia de funciones tiene sus propios atributos únicos y las estudiaremos todas con gran detalle. El propósito de la discusión de esta sección, entonces, es sentar las bases para ese estudio adicional investigando aspectos del comportamiento funcional que se aplican a todas las funciones. Para comenzar, examinaremos los conceptos de aumento, disminución y constante. Antes de definir los conceptos algebraicamente, es instructivo mirarlos primero gráficamente. Considera la gráfica de la función\(\ f\) a continuación.
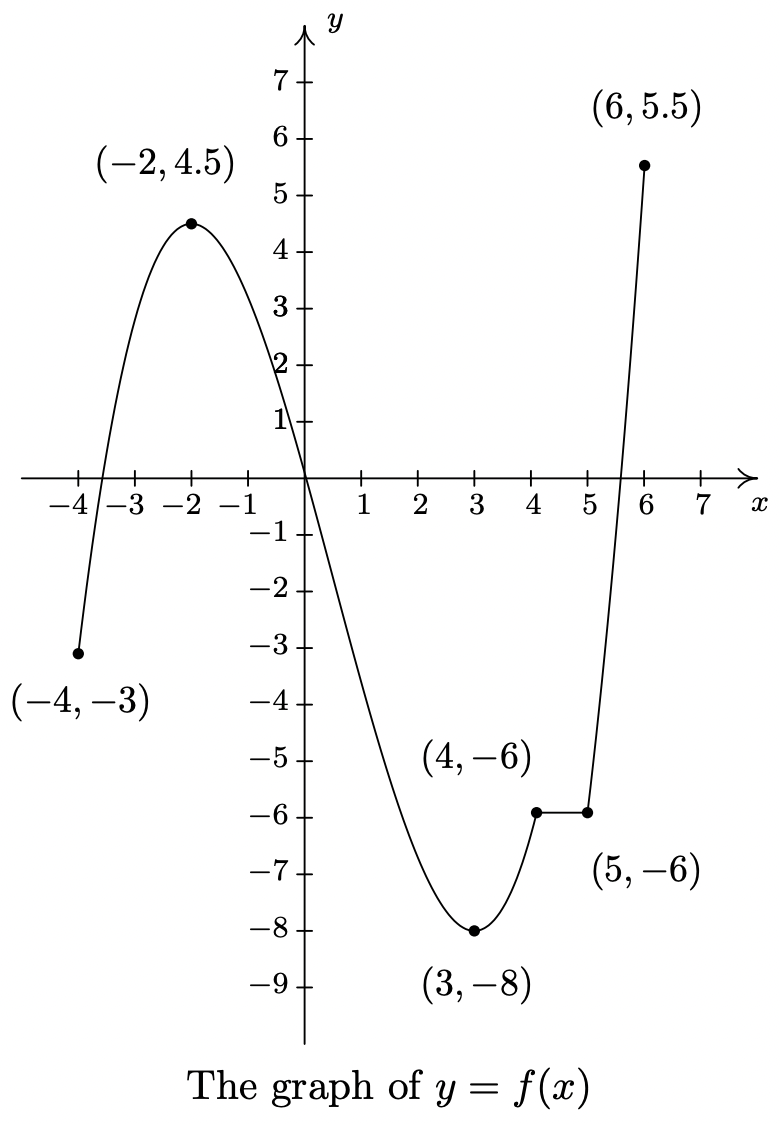
Leyendo de izquierda a derecha, la gráfica 'comienza' en el punto (−4, −3) y 'termina' en el punto (6, 5.5). Si imaginamos caminar de izquierda a derecha en la gráfica, entre (−4, −3) y (−2, 4.5), estamos caminando 'cuesta arriba'; luego entre (−2, 4.5) y (3, −8), estamos caminando 'cuesta abajo'; y entre (3, −8) y (4, −6), estamos caminando 'cuesta arriba' una vez más. De (4, −6) a (5, −6), nos 'nivelamos', y luego retomamos caminar 'cuesta arriba' de (5, −6) a (6, 5.5). En otras palabras, para los valores x entre −4 y −2 (inclusive), las coordenadas y en la gráfica son cada vez más grandes, o aumentando, a medida que nos movemos de izquierda a derecha. Ya que\(\ y = f(x)\), los valores y en la gráfica son los valores de la función, y decimos que la función\(\ f\) está aumentando en el intervalo [−4, −2]. Análogamente, decimos que\(\ f\) está disminuyendo en el intervalo [−2, 3] aumentando una vez más en el intervalo [3, 4], constante en [4, 5], y finalmente aumentando una vez más en [5, 6]. Es extremadamente importante notar que el comportamiento (creciente, decreciente o constante) ocurre en un intervalo en el eje x. Cuando decimos que la función\(\ f\) está aumentando en [−4, −2] no mencionamos\(\ y\) los valores reales que\(\ f\) alcanza en el camino. Así, reportamos dónde ocurre el comportamiento, no en qué medida ocurre el comportamiento. 7 Observe también que no decimos que una función va en aumento, decreciente o constante a un solo valor x. De hecho, nos encontraríamos con serios problemas en nuestro ejemplo anterior si intentáramos hacerlo porque\(\ x = −2\) está contenido en un intervalo en el que\(\ f\) iba en aumento y uno en el que está disminuyendo. (Hay más sobre este tema —y muchos otros— en los Ejercicios.)
Ahora estamos listos para las definiciones algebraicas más formales de lo que significa que una función sea creciente, decreciente o constante.
Supongamos que\(\ f\) es una función definida en un intervalo\(\ I\). Decimos que\(\ f\) es:
- aumentando en\(\ I\) si y solo si\(\ f(a) < f(b)\) para todos los números reales\(\ a\),\(\ b\) en\(\ I\) con\(\ a < b\).
- disminuyendo en\(\ I\) si y solo si\(\ f(a) > f(b)\) para todos los números reales\(\ a\),\(\ b\) en\(\ I\) con\(\ a < b\).
- constante en\(\ I\) si y solo si\(\ f(a) = f(b)\) para todos los números reales\(\ a\),\(\ b\) en\(\ I\).
Vale la pena tomarse un tiempo para ver que las descripciones algebraicas de incremento, decreciente y constante como se indica en la Definición 1.10 concuerdan con nuestras descripciones gráficas dadas anteriormente. Debe mirar hacia atrás a través de los ejemplos y conjuntos de ejercicios en secciones anteriores donde se dieron gráficos para ver si puede determinar los intervalos en los que las funciones están aumentando, disminuyendo o constantes. ¿Se puede encontrar un ejemplo de una función para la que no se aplica ninguno de los conceptos de la Definición 1.10?
Ahora volvamos nuestra atención a algunos de los puntos de la gráfica. Claramente el punto (−2, 4.5) no tiene el mayor\(\ y\) valor de todos los puntos en la gráfica de\(\ f\) − de hecho ese honor va a (6, 5.5) − pero (−2, 4.5) debería obtener algún tipo de premio de consolación por ser 'la cima de la colina' entre\(\ x = −4\) y\(\ x = 3\). Decimos que la función f tiene un máximo local 8 en el punto (−2, 4.5), porque la coordenada y 4.5 es el valor y más grande (de ahí, el valor de la función) en la curva 'cerca' 9\(\ x = −2\). Del mismo modo, decimos que la función f tiene un mínimo local 10 en el punto (3, −8), ya que la coordenada y −8 es el valor de función más pequeño cercano\(\ x = 3\). Si bien es tentador decir que los extremos locales 11 ocurren cuando la función cambia de aumentar a disminuir o viceversa, no es una manera suficientemente precisa de definir los conceptos para las necesidades del Cálculo. A riesgo de ser pedantes, presentaremos las definiciones tradicionales y examinaremos a fondo las patologías que inducen en los Ejercicios. Tenemos una última observación que hacer antes de proceder a las definiciones algebraicas y mirar un ejemplo bastante manso, pero útil.
Si miramos toda la gráfica, vemos que el\(\ y\) valor más grande (el valor de función más grande) es 5.5 at\(\ x = 6\). En este caso, decimos que el máximo 12 de f es 5.5; de manera similar, el mínimo 13 de\(\ f\) es −8.
Formalizamos estos conceptos en las siguientes definiciones.
Supongamos que\(\ f\) es una función con\(\ f(a) = b\).
- Decimos que\(\ f\) tiene un máximo local en el punto\(\ (a, b)\) si y sólo si hay un intervalo abierto\(\ I\) que contiene un para el cual\(\ f(a) ≥ f(x)\) para todos\(\ x\) en\(\ I\). El valor\(\ f(a) = b\) se denomina 'un valor máximo local de\(\ f’\) en este caso.
- Decimos que\(\ f\) tiene un mínimo local en el punto\(\ (a, b)\) si y solo si hay un intervalo abierto\(\ I\) que contiene\(\ a\) para cual\(\ f(a) ≤ f(x)\) para todos\(\ x\) en\(\ I\). El valor\(\ f(a) = b\) se denomina 'un valor mínimo local de\(\ f’\) en este caso.
- El valor\(\ b\) se llama el máximo de\(\ f\) si\(\ b ≥ f(x)\) para todos\(\ x\) en el dominio de\(\ f\).
- El valor\(\ b\) se llama el mínimo de\(\ f\) si\(\ b ≤ f(x)\) para todos\(\ x\) en el dominio de\(\ f\).
Es importante tener en cuenta que no todas las funciones tendrán todas estas características. En efecto, ¡es posible tener una función sin ningún extremo local o absoluto en absoluto! (¿Alguna idea de cómo tendría que ser la gráfica de una función de este tipo?) Veremos ejemplos de funciones en los Ejercicios que tienen una o dos, pero no todas, de estas características, algunas que tienen instancias de cada tipo de extremo y algunas funciones que parecen desafiar el sentido común. En todos los casos, sin embargo, nos adheriremos a las definiciones algebraicas anteriores mientras exploramos la maravillosa diversidad de gráficas que las funciones nos proporcionan.
Aquí está el ejemplo 'manso' que se prometió antes. Resume todos los conceptos presentados en esta sección así como algunos de secciones anteriores por lo que debes dedicar un tiempo a pensarlo profundamente antes de proceder a los Ejercicios.
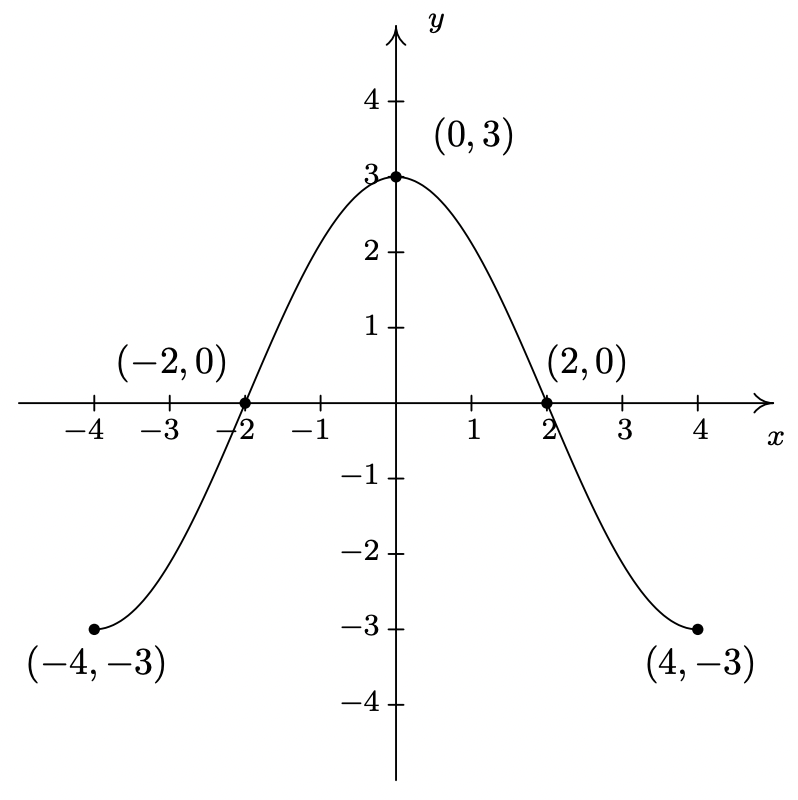
Dada la gráfica de\(\ y = f(x)\) abajo, conteste todas las siguientes preguntas.
- Encuentra el dominio de\(\ f\).
- Encuentra la gama de\(\ f\).
- Enumere las intercepciones x, si existe alguna.
- Enumere las intercepciones y, si existe alguna.
- Encuentra los ceros de\(\ f\).
- Resolver\(\ f(x) < 0\).
- Determinar\(\ f(2)\).
- Resolver\(\ f(x) = −3\).
- Encuentre la cantidad de soluciones para\(\ f(x) = 1\).
- ¿\(\ f\)Parece ser par, impar, o ninguno?
- Enumere los intervalos en los que\(\ f\) va en aumento.
- Enumere los intervalos en los que\(\ f\) está disminuyendo.
- Enumere los máximos locales, si los hay.
- Enumere los mínimos locales, si los hay.
- Encuentra el máximo, si existe.
- Encuentra el mínimo, si existe.
Solución
- Para encontrar el dominio de\(\ f\), procedemos como en la Sección 1.3. Al proyectar la gráfica al eje x, vemos que la porción del eje x que corresponde a un punto en la gráfica es todo, desde −4 hasta 4, inclusive. De ahí que el dominio sea [−4, 4].
- Para encontrar el rango, proyectamos la gráfica al eje y. Vemos que los\(\ y\) valores de −3 a 3, inclusive, constituyen el rango de\(\ f\). De ahí que nuestra respuesta sea [−3, 3].
- Las intercepciones x son los puntos en la gráfica con la coordenada y 0, es decir (−2, 0) y (2, 0).
- La intercepción y es el punto en la gráfica con la coordenada x 0, es decir (0, 3).
- Los ceros de\(\ f\) son las coordenadas x de las intercepciones x de la gráfica de las\(\ y = f(x)\) cuales son x = −2, 2.
- Para resolverlo\(\ f(x) < 0\), buscamos los\(\ x\) valores de los puntos en la gráfica donde la coordenada y es menor que 0. Gráficamente, estamos buscando dónde está la gráfica por debajo del eje x. Esto sucede para los\(\ x\) valores de −4 a −2 y nuevamente de 2 a 4. Entonces nuestra respuesta es\(\ [-4,-2) \cup(2,4]\).
- Dado que la gráfica de f es la gráfica de la ecuación\(\ y = f(x)\),\(\ f(2)\) es la coordenada y del punto que corresponde a\(\ x = 2\). Ya que el punto (2, 0) está en la gráfica, tenemos\(\ f(2) = 0\).
- Para resolver\(\ f(x) = −3\), miramos dónde\(\ y = f(x) = −3\). Encontramos dos puntos con una coordenada y de −3, a saber (−4, −3) y (4, −3). De ahí que las soluciones\(\ f(x) = −3\) sean\(\ x=\pm 4\).
- Al igual que en el problema anterior\(\ f(x) = 1\), para resolver, buscamos puntos en la gráfica donde la coordenada y es 1. A pesar de que estos puntos no están especificados, vemos que la curva tiene dos puntos con un\(\ y\) valor de 1, como se ve en la gráfica de abajo. Eso significa que hay dos soluciones para\(\ f(x) = 1\).
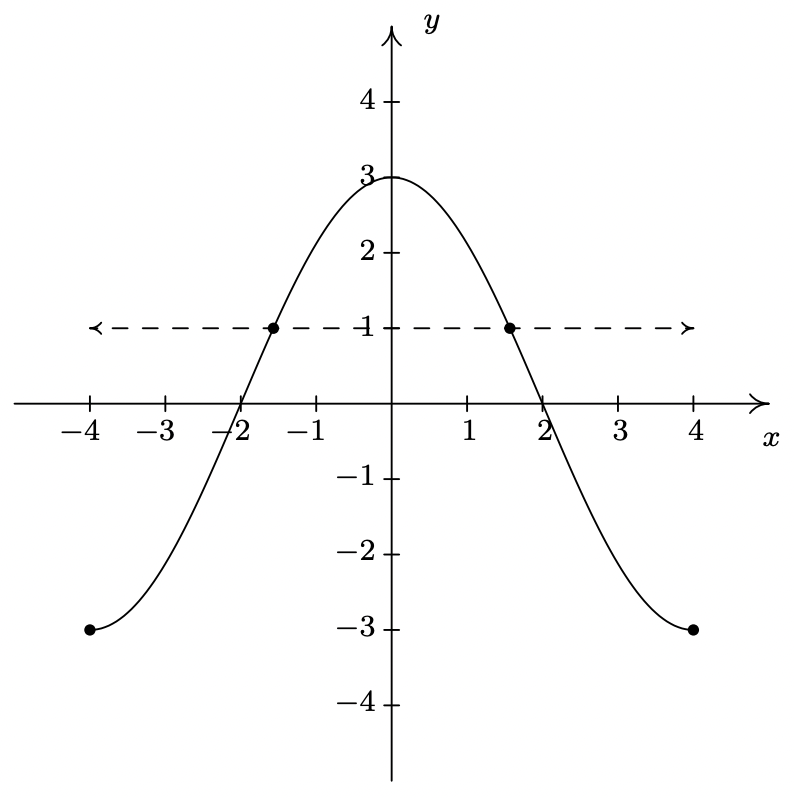
- La gráfica parece ser simétrica alrededor del eje y. Esto sugiere 14 que f es par.
- A medida que nos movemos de izquierda a derecha, la gráfica se eleva de (−4, −3) a (0, 3). Este medio\(\ f\) está aumentando en el intervalo [−4, 0]. (Recuerde, la respuesta aquí es un intervalo en el eje x).
- A medida que nos movemos de izquierda a derecha, la gráfica cae de (0, 3) a (4, −3). Esta media\(\ f\) es decreciente en el intervalo [0, 4]. (Recuerde, la respuesta aquí es un intervalo en el eje x).
- La función tiene su único máximo local en (0, 3) así\(\ f(0) = 3\) es el valor mínimo local.
- No hay mínimos locales. ¿Por qué no cuentan (−4, −3) y (4, −3)? Consideremos el punto (−4, −3) por un momento. Recordemos que, en la definición de mínimo local, necesita haber un intervalo abierto I que contenga x = −4 tal que\(\ f(−4) < f(x)\) para todos\(\ x\) en\(\ I\) diferente de −4. Pero si ponemos un intervalo abierto alrededor de\(\ x = −4\) una porción de ese intervalo quedará fuera del dominio de\(\ f\). Debido a que no podemos cumplir con los requisitos de la definición para un mínimo local, no podemos afirmar que\(\ f\) tiene uno en (−4, −3). El punto (4, −3) falla por la misma razón − ningún intervalo abierto alrededor\(\ x = 4\) permanece dentro del dominio de\(\ f\).
- El valor máximo de\(\ f\) es la coordenada y más grande que es 3.
- El valor mínimo de\(\ f\) es la coordenada y más pequeña que es −3.
Con pocas excepciones, no desarrollaremos técnicas en Álgebra Universitaria que nos permitan determinar los intervalos en los que una función está aumentando, disminuyendo o constante o encontrar analíticamente los máximos locales y mínimos locales; este es el negocio de Cálculo. 15 Cuando tengamos que encontrar tales bestias, recurriremos a la calculadora. La mayoría de las calculadoras gráficas tienen características 'Mínimas' y 'Máximas' que se pueden utilizar para aproximar estos valores, como ahora demostramos.
Vamos\(\ f(x)=\frac{15 x}{x^{2}+3}\). Utilice una calculadora gráfica para aproximar los intervalos en los que\(\ f\) está aumentando y aquellos en los que está disminuyendo. Aproximado todos los Extremos.
Solución
Ingresar esta función en la calculadora da
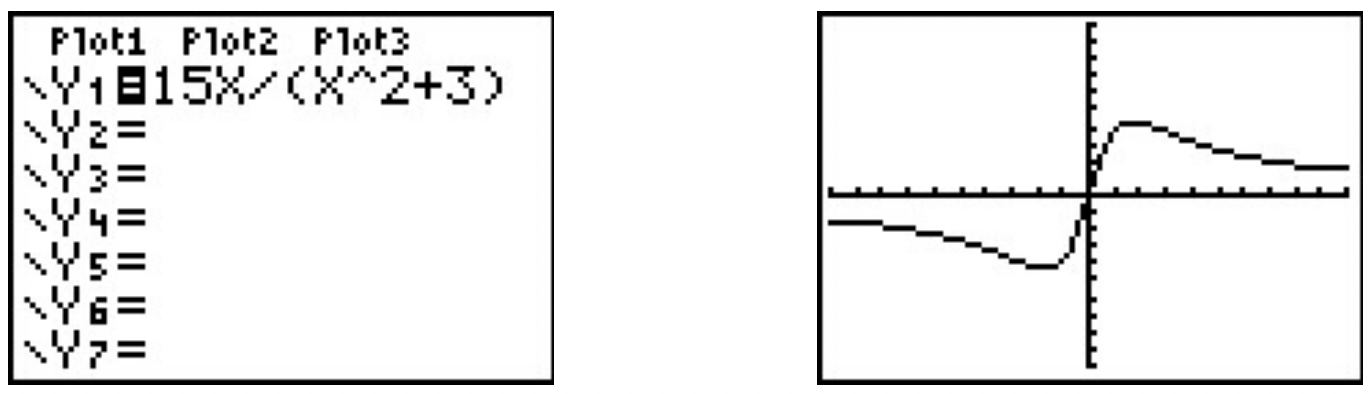
Usando las características Mínimas y Máximas, obtenemos
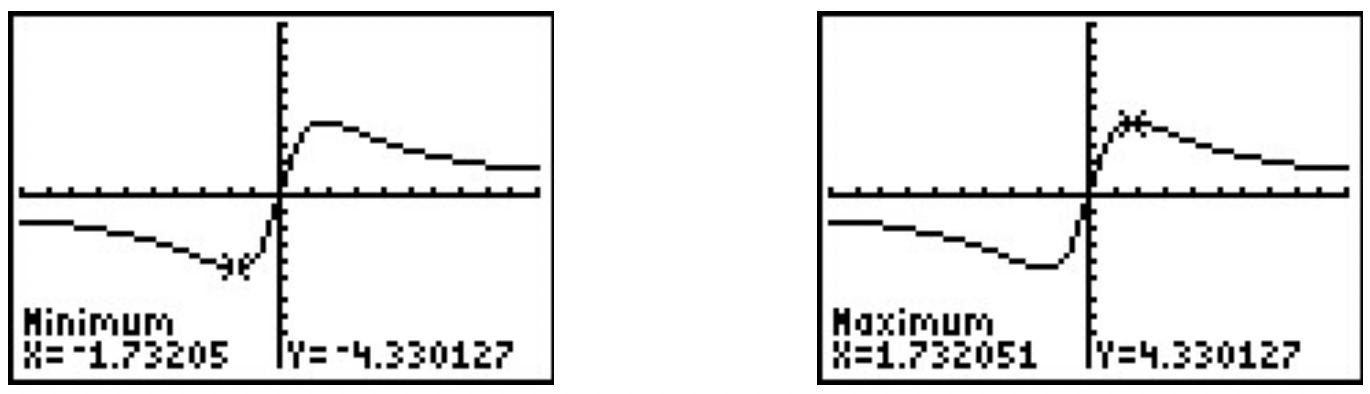
A dos decimales,\(\ f\) parece tener su único mínimo local en (−1.73, −4.33) y su único máximo local en (1.73, 4.33). Dada la simetría sobre el origen que sugiere la gráfica, la relación entre estos puntos no debería ser demasiado sorprendente. La función parece estar aumentando en [−1.73, 1.73] y disminuyendo en\(\ (-\infty,-1.73] \cup[1.73, \infty)\). Esto hace −4.33 el mínimo (absoluto) y 4.33 el máximo (absoluto).
Encuentra los puntos en la gráfica de los\(\ y=(x-3)^{2}\) cuales están más cerca del origen. Redondee sus respuestas a dos decimales.
Solución
Supongamos que un punto\(\ (x, y)\) está en la gráfica de\(\ y=(x-3)^{2}\). Su distancia al origen (0, 0) viene dada por
\ (\\ begin {alineado}
d &=\ sqrt {(x-0) ^ {2} + (y-0) ^ {2}}\\
&=\ sqrt {x^ {2} +y^ {2}}\\
&=\ sqrt {x^ {2} +\ left [(x-3) ^ {2}\ derecha] ^ {2}}\ quad\ texto {Desde y} =( x-3) ^ {2}\\
&=\ sqrt {x^ {2} + (x-3) ^ {4}}
\ end {alineado}\)
Dado un valor para\(\ x\), la fórmula\(\ d=\sqrt{x^{2}+(x-3)^{4}}\) es la distancia de (0, 0) al punto (x, y) en la curva\(\ y=(x-3)^{2}\). Lo que hemos definido, entonces, es una función\(\ d(x)\) que deseamos minimizar sobre todos los valores de\(\ x\). Para llevar a cabo esta tarea analíticamente requeriría Cálculo por lo que como hemos mencionado anteriormente, podemos usar una calculadora gráfica para encontrar una solución aproximada. Usando la calculadora, ingresamos la función\(\ d(x)\) como se muestra a continuación y graficamos.
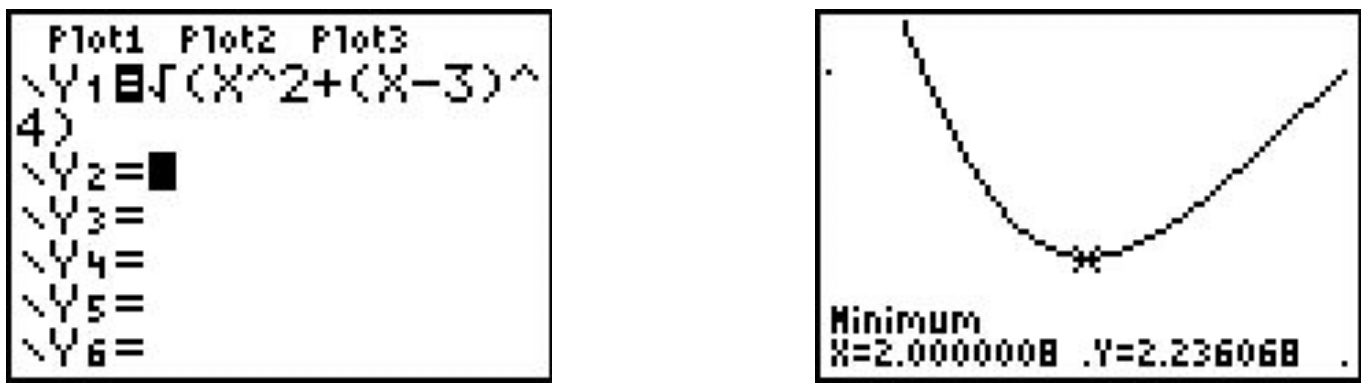
Usando la función Mínimo, vemos arriba a la derecha que el mínimo (absoluto) ocurre cerca\(\ x = 2\). Redondeando a dos decimales, obtenemos que la distancia mínima ocurre cuando\(\ x = 2.00\). Para encontrar el valor y en la parábola asociada a\(\ x = 2.00\), sustituimos 2.00 en la ecuación para obtener\(\ y=(x-3)^{2}=(2.00-3)^{2}=1.00\). Entonces, nuestra respuesta final es (2.00, 1.00). 16 (¿Qué significa en este problema el\(\ y\) valor que aparece en la pantalla de la calculadora?)
1.6.2 Ejercicios
En los Ejercicios 1 - 12, esboce la gráfica de la función dada. Indicar el dominio de la función, identificar cualquier intercepción y probar la simetría. \
- \(\ f(x) = 2 − x\)
- \(\ f(x)=\frac{x-2}{3}\)
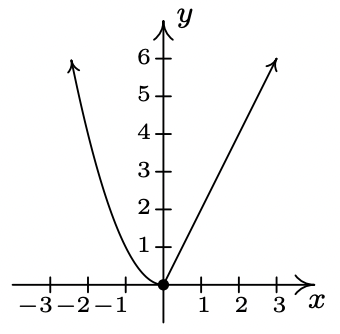
- \(\ f(x)=x^{2}+1\)
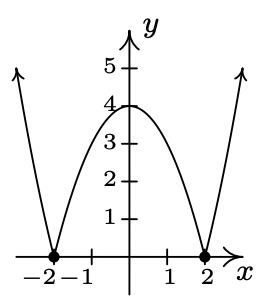
- \(\ f(x)=4-x^{2}\)
- \(\ f(x) = 2\)
- \(\ f(x)=x^{3}\)
- \(\ f(x) = x(x − 1)(x + 2)\)
- \(\ f(x)=\sqrt{x-2}\)
- \(\ f(x)=\sqrt{5-x}\)
- \(\ f(x)=3-2 \sqrt{x+2}\)
- \(\ f(x)=\sqrt[3]{x}\)
- \(\ f(x)=\frac{1}{x^{2}+1}\)
En Ejercicios 13 - 20, esboce la gráfica de la función definida por partes dada.
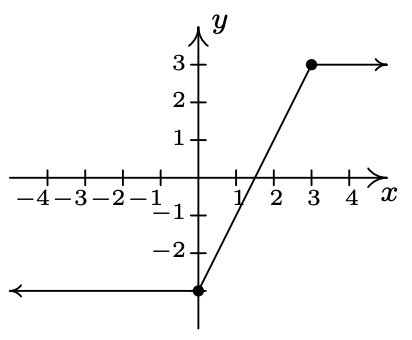
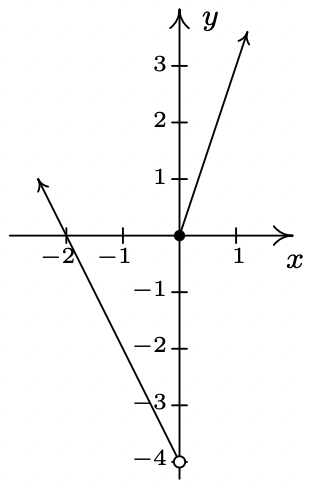
- \ (\ f (x) =\ left\ {\ begin {array} {rlr}
4-x &\ text {if} & x\ leq 3\\
2 &\ text {if} & x>3
\ end {array}\ right.\) - \ (\ f (x) =\ left\ {\ begin {array} {lll}
x^ {2} &\ text {if} & x\ leq 0\\
2 x &\ text {if} & x>0
\ end {array}\ right.\) - \ (\ f (x) =\ left\ {\ begin {array} {rll}
-3 &\ text {if} & x<0\\
2 x-3 &\ text {if} & 0\ leq x\ leq 3\\
3 &\ text {if} & x>3
\ end {array}\ right.\) - \ (\ f (x) =\ left\ {\ begin {array} {lll}
x^ {2} -4 &\ text {if} & x\ leq-2\\
4-x^ {2} &\ text {if} & -2<x<2\
x^ {2} -4 &\ text {if} & x\ geq 2
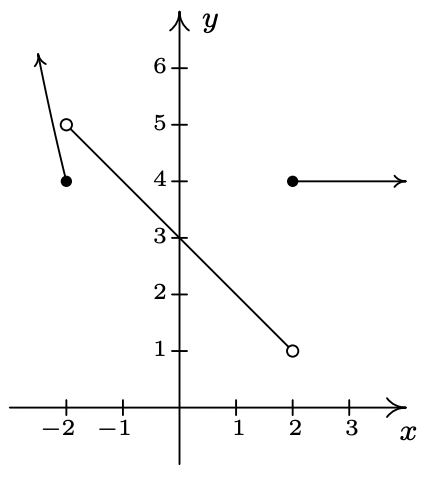
\ end {array}\ derecha.\) - \ (\ f (x) =\ left\ {\ begin {array} {rll}
-2 x-4 &\ text {if} & x<0\
3 x &\ text {if} & x\ geq 0
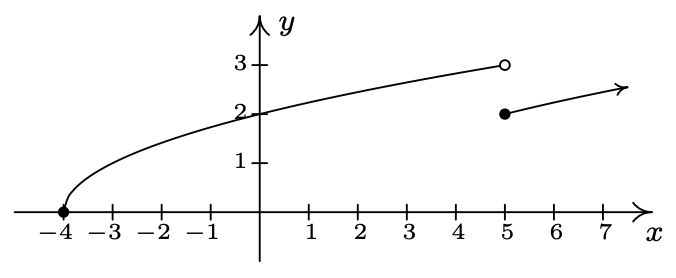
\ end {array}\ right.\) - \ (\ f (x) =\ left\ {\ begin {array} {lll}
\ sqrt {x+4} &\ text {if} & -4\ leq x<5\\
\ sqrt {x-1} &\ text {if} & x\ geq 5
\ end {array}\ right.\) - \ (\ f (x) =\ left\ {\ begin {array} {rll}
x^ {2} &\ text {if} & x\ leq-2\\
3-x &\ text {if} & -2<x<2\\
4 &\ text {if} & x\ geq 2
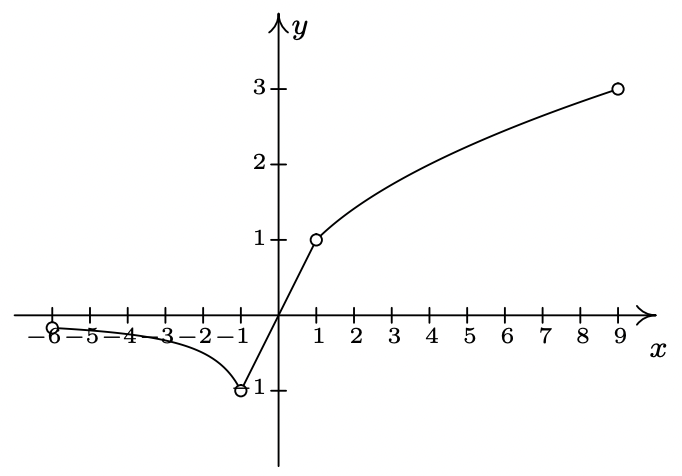
\ end {array}\ right.\) - \ (\ f (x) =\ left\ {\ begin {array} {rll}
\ frac {1} {x} &\ text {if} & -6<x<-1\\
x &\ text {if} & -1<x<1\
\ sqrt {x} &\ text {if} & 1<x<9
\ end {array}\ derecho.\)
En los Ejercicios 21 - 41, determinar analíticamente si las siguientes funciones son pares, impares o ninguna.
- \(\ f(x) = 7x\)
- \(\ f(x) = 7x + 2\)
- \(\ f(x) = 7\)
- \(\ f(x)=3 x^{2}-4\)
- \(\ f(x)=4-x^{2}\)
- \(\ f(x)=x^{2}-x-6\)
- \(\ f(x)=2 x^{3}-x\)
- \(\ f(x)=-x^{5}+2 x^{3}-x\)
- \(\ f(x)=x^{6}-x^{4}+x^{2}+9\)
- \(\ f(x)=x^{3}+x^{2}+x+1\)
- \(\ f(x)=\sqrt{1-x}\)
- \(\ f(x)=\sqrt{1-x^{2}}\)
- \(\ f(x) = 0\)
- \(\ f(x)=\sqrt[3]{x}\)
- \(\ f(x)=\sqrt[3]{x^{2}}\)
- \(\ f(x)=\frac{3}{x^{2}}\)
- \(\ f(x)=\frac{2 x-1}{x+1}\)
- \(\ f(x)=\frac{3 x}{x^{2}+1}\)
- \(\ f(x)=\frac{x^{2}-3}{x-4 x^{3}}\)
- \(\ f(x)=\frac{9}{\sqrt{4-x^{2}}}\)
- \(\ f(x)=\frac{\sqrt[3]{x^{3}+x}}{5 x}\)
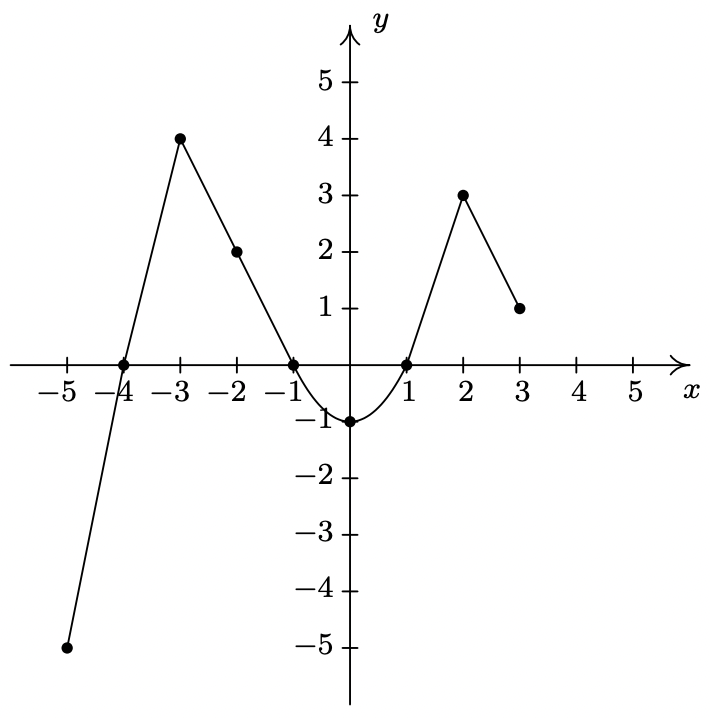
En Ejercicios 42 - 57, utilice la gráfica que\(\ y = f(x)\) se da a continuación para responder a la pregunta.
- Encuentra el dominio de\(\ f\).
- Encuentra la gama de\(\ f\).
- Determinar\(\ f(−2)\).
- Resolver\(\ f(x) = 4\).
- Enumere las intercepciones x, si existe alguna.
- Enumere las intercepciones y, si existe alguna.
- Encuentra los ceros de\(\ f\).
- Resolver\(\ f(x) ≥ 0\).
- Encuentre la cantidad de soluciones para\(\ f(x) = 1\).
- ¿\(\ f\)Parece ser par, impar, o ninguno?
- Enumere los intervalos donde\(\ f\) está aumentando.
- Enumere los intervalos donde\(\ f\) está disminuyendo.
- Enumere los máximos locales, si los hay.
- Enumere los mínimos locales, si los hay.
- Encuentra el máximo, si existe.
- Encuentra el mínimo, si existe.
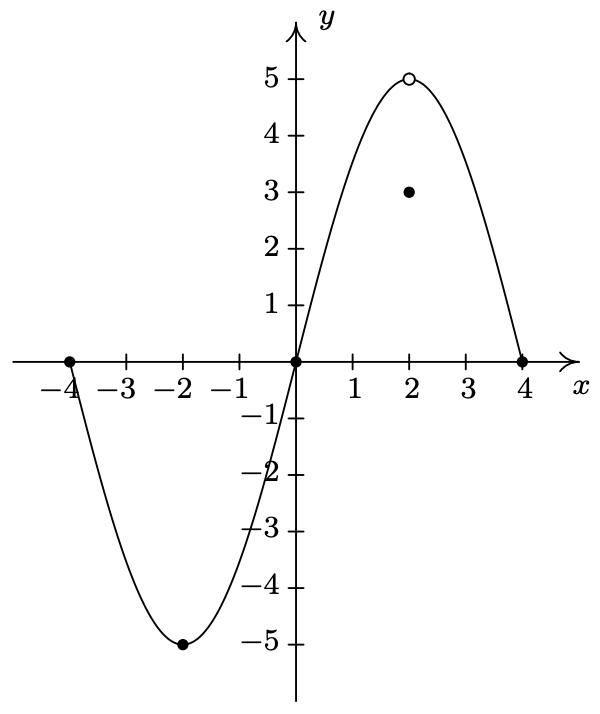
En Ejercicios 58 - 73, utilice la gráfica que\(\ y = f(x)\) se da a continuación para responder a la pregunta.
- Encuentra el dominio de\(\ f\).
- Encuentra la gama de\(\ f\).
- Determinar\(\ f(2)\).
- Resolver\(\ f(x) = −5\).
- Enumere las intercepciones x, si existe alguna.
- Enumere las intercepciones y, si existe alguna.
- Encuentra los ceros de\(\ f\).
- Resolver\(\ f(x) ≤ 0\).
- Encuentre la cantidad de soluciones para\(\ f(x) = 3\).
- ¿\(\ f\)Parece ser par, impar, o ninguno?
- Enumere los intervalos donde\(\ f\) está aumentando.
- Enumere los intervalos donde\(\ f\) está disminuyendo.
- Enumere los máximos locales, si los hay.
- Enumere los mínimos locales, si los hay.
- Encuentra el máximo, si existe.
- Encuentra el mínimo, si existe.
En los Ejercicios 74 - 77, usa tu calculadora gráfica para aproximar los extremos locales y absolutos de la función dada. Aproximar los intervalos en los que la función está aumentando y aquellos en los que está disminuyendo. Redondee sus respuestas a dos decimales.
- \(\ f(x)=x^{4}-3 x^{3}-24 x^{2}+28 x+48\)
- \(\ f(x)=x^{2 / 3}(x-4)\)
- \(\ f(x)=\sqrt{9-x^{2}}\)
- \(\ f(x)=x \sqrt{9-x^{2}}\)
En Ejercicios 78 - 85, utilice las gráficas de\(\ y = f(x)\) y\(\ y = g(x)\) siguientes para encontrar el valor de la función.
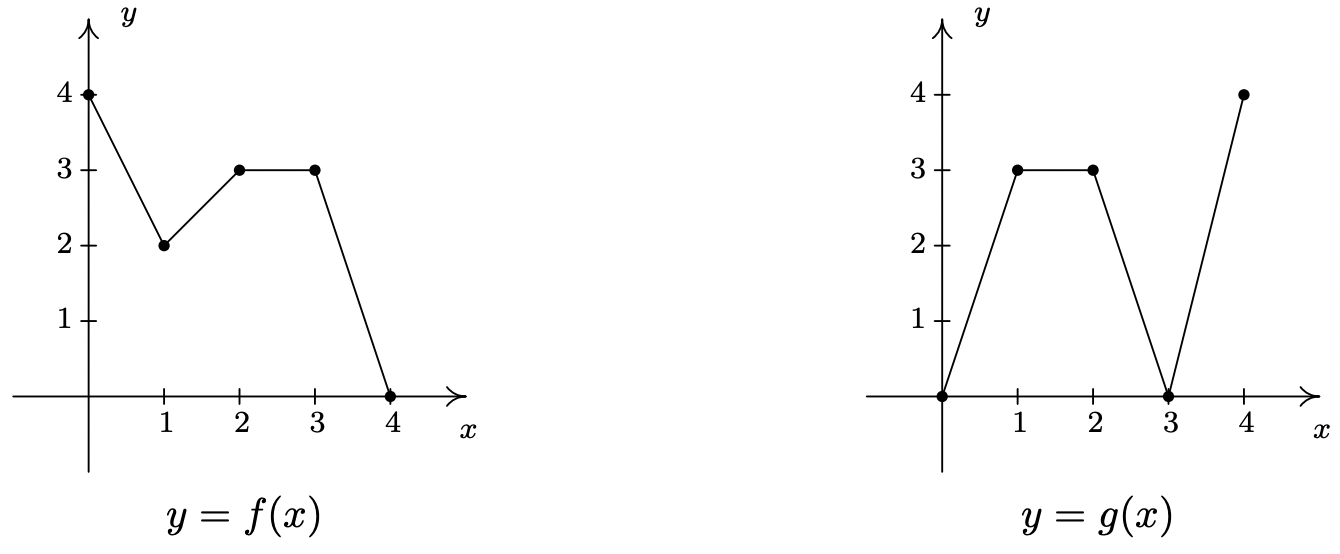
- \(\ (f + g)(0)\)
- \(\ (f + g)(1)\)
- \(\ (f − g)(1)\)
- \(\ (g − f)(2)\)
- \(\ (fg)(2)\)
- \(\ (fg)(1)\)
- \(\ \left(\frac{f}{g}\right)(4)\)
- \(\ \left(\frac{g}{f}\right)(2)\)
La siguiente gráfica representa la altura\(\ h\) de un Sasquatch (en pies) en función de su edad\(\ N\) en años. Úsalo para responder a las preguntas de los Ejercicios 86 - 90.
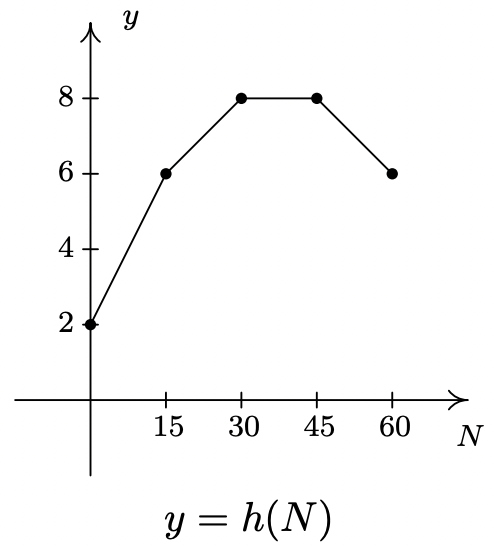
- Encontrar e interpretar\(\ h(0)\).
- ¿Qué tan alta es la Sasquatch cuando tiene 15 años?
- Resolver\(\ h(N) = 6\) e interpretar.
- Enumere el intervalo sobre el cual\(\ h\) es constante e interprete su respuesta.
- Enumere el intervalo sobre el cual\(\ h\) está disminuyendo e interprete su respuesta.
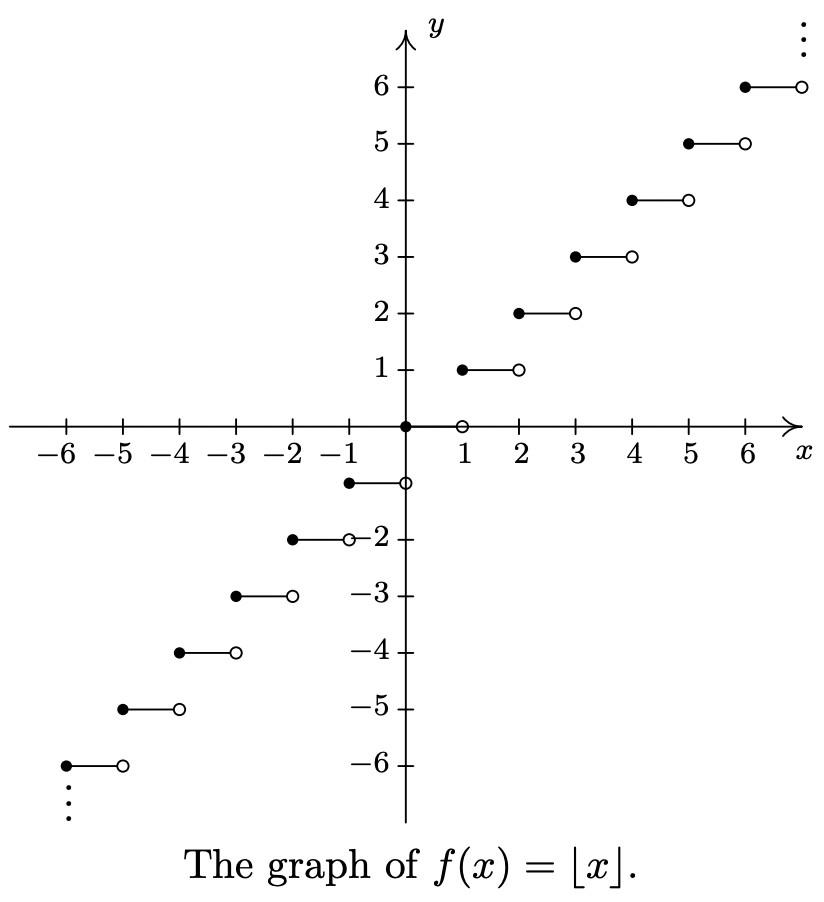
Para los Ejercicios 91 - 93, deja\(\ f(x)=\lfloor x\rfloor\) ser la mayor función entera como se define en el Ejercicio 75 en la Sección 1.4.
- Gráfica\(\ y = f(x)\). Tenga cuidado de describir correctamente el comportamiento de la gráfica cerca de los enteros.
- ¿Es\(\ f\) par, impar, o ninguno? Explique.
- Discuta con sus compañeros de clase qué puntos en la gráfica son mínimos locales, máximos locales o ambos. ¿Cada\(\ f\) vez va en aumento? ¿Disminuyendo? ¿Constante?
En los Ejercicios 94 - 95, usa tu calculadora gráfica para mostrar que la función dada no tiene ningún extremo, ni local ni absoluto.
- \(\ f(x)=x^{3}+x-12\)
- \(\ f(x)=-5 x+2\)
- En el Ejercicio 71 de la Sección 1.4, vimos que la población de Sasquatch en el Condado de Portage podría ser modelada por la función\(\ P(t)=\frac{150 t}{t+15}\), donde\(\ t = 0\) representa el año 1803. Utilice su calculadora gráfica para analizar el comportamiento general de la función de\(\ P\). ¿Alguna vez habrá un momento en que 200 Sasquatch deambulen por el condado de Portage?
- Supongamos\(\ f\) y ambas\(\ g\) son funciones pares. ¿Qué se puede decir de las funciones\(\ f + g\),\(\ f − g\),\(\ fg\) y\(\ \frac{f}{g}\)? ¿\(\ f\)Y si g son impares? ¿Y si f es par pero g es impar?
- Uno de los aspectos más importantes del Plano de Coordenadas Cartesianas es su capacidad para poner Álgebra en términos geométricos y Geometría en términos algebraicos. Hemos pasado la mayor parte de este capítulo mirando este mismo fenómeno y ahora deberías pasar algún tiempo con tus compañeros revisando lo que hemos hecho. ¿Qué resultados principales tenemos que unen Álgebra y Geometría? ¿Qué conceptos de Geometría aún no hemos descrito algebraicamente? ¿Qué temas de Álgebra Intermedia aún no hemos discutido geométricamente?
Ahora es el momento de “examinar a fondo las patologías inducidas” por las definiciones precisas de máximo local y mínimo local. Lo haremos proporcionándote a ti y a tus compañeros de clase una serie de Ejercicios para discutir. Deberá volver a referirse a la Definición 1.10 (Aumentando, Disminuyendo y Constante) y Definición 1.11 (Máxima y Mínima) durante la discusión.
- Considera la gráfica de la función que\(\ f\) se da a continuación.
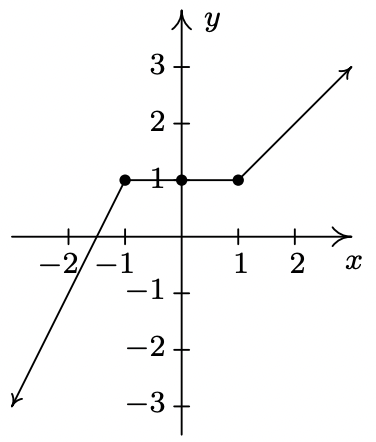
- Mostrar que\(\ f\) tiene un máximo local pero no un mínimo local en el punto (−1, 1).
- Demostrar que\(\ f\) tiene un mínimo local pero no un máximo local en el punto (1, 1).
- Demostrar que\(\ f\) tiene un máximo local Y un mínimo local en el punto (0, 1).
- Mostrar que\(\ f\) es constante en el intervalo [−1, 1] y así tiene tanto un máximo local como un mínimo local en cada punto\(\ (x, f(x))\) donde\(\ −1 < x < 1\).
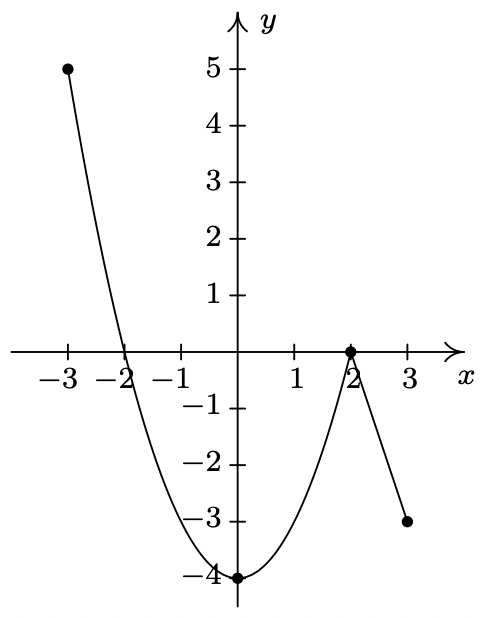
- Usando el Ejemplo 1.6.4 como guía, mostrar que la función g cuya gráfica se da a continuación no tiene un máximo local en (−3, 5) ni tiene un mínimo local en (3, −3). Encuentra su extrema, tanto local como absoluta. ¿Qué tiene de único el punto (0, −4) en esta gráfica? También encuentra los intervalos en los que\(\ g\) va en aumento y aquellos en los que\(\ g\) va disminuyendo.
- Dijimos anteriormente en el apartado que no es suficientemente bueno decir que existen extremos locales donde una función cambia de aumentar a disminuir o viceversa. Como demostró un ejercicio anterior, podríamos tener extremos locales cuando una función es constante por lo que ahora necesitamos examinar algunas funciones cuyas gráficas realmente cambian de dirección. Considera las funciones que se muestran a continuación. Observe que los cuatro cambian de dirección en un círculo abierto en la gráfica. Examine cada uno para los extrema locales. ¿Cuál es el efecto de colocar el “punto” en el eje y encima o debajo del círculo abierto? ¿Qué podría decir si no se asignara ningún valor de función\(\ x = 0\)?
- Función I
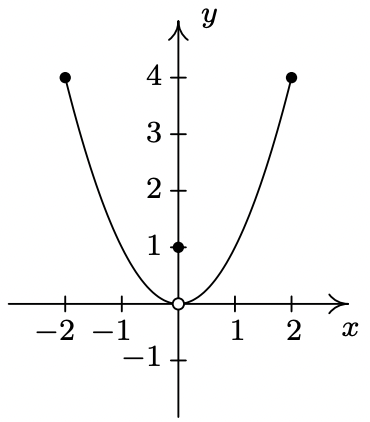
- Función II
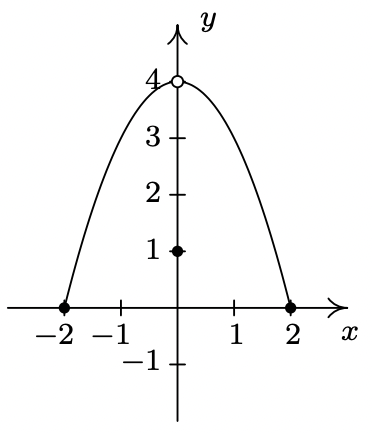
- Función III
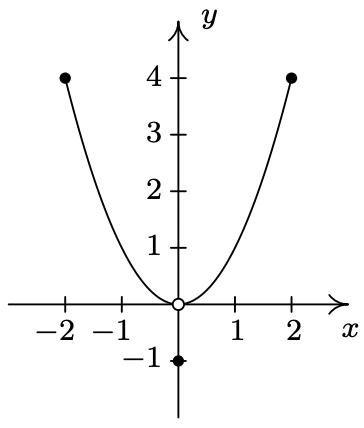
- Función IV
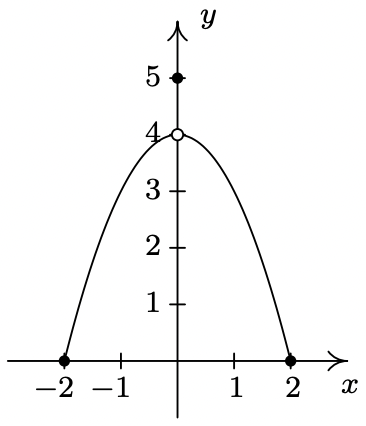
- Función I
1.6.3 Respuestas
- \(\ f(x) = 2 − x\)
Dominio:\\(\ (-\infty, \infty)\)
intercepción x: (2, 0)
intercepción en Y: (0, 2)
Sin simetría
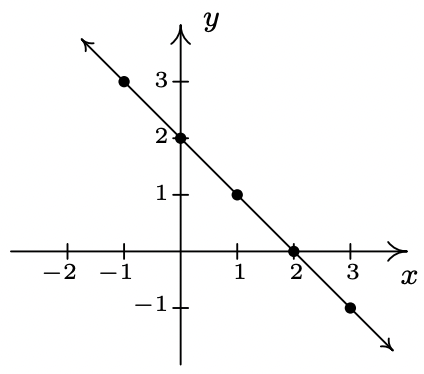
- \(\ f(x)=\frac{x-2}{3}\)
Dominio:\\(\ (-\infty, \infty)\)
intercepción x: (2, 0)
Intercepción en Y:\(\ \left(0,-\frac{2}{3}\right)\)
Sin simetr
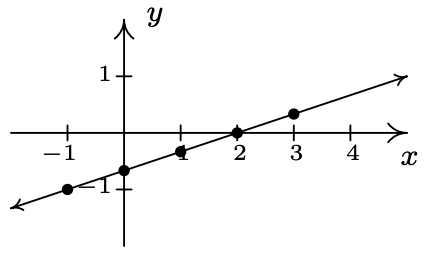
- \(\ f(x)=x^{2}+1\)
Dominio:\\(\ (-\infty, \infty)\)
x-intercept: Ninguno
intercepción en Y: (0, 1)
Incluso
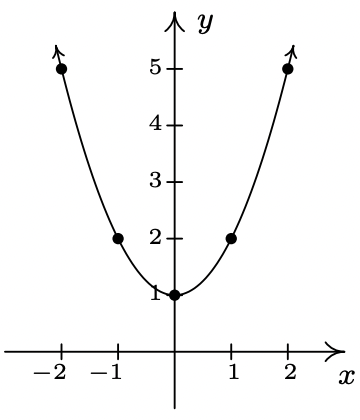
- \(\ f(x)=4-x^{2}\)
Dominio:\\(\ (-\infty, \infty)\)
intercepciones x: (−2, 0), (2, 0)
intercepción en Y: (0, 4)
Incluso
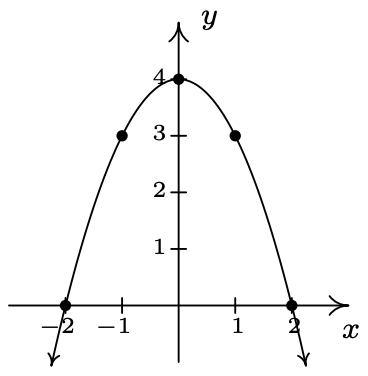
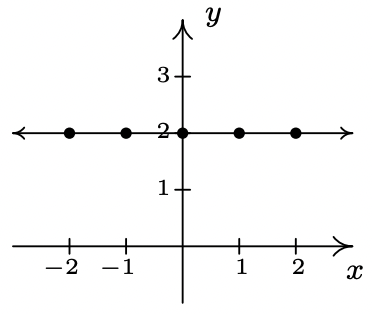
- \(\ f(x) = 2\)
Dominio:\\(\ (-\infty, \infty)\)
x-intercept: Ninguno
intercepción en Y: (0, 2)
Incluso
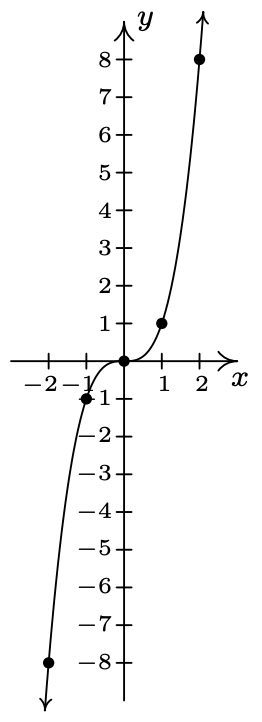
- \(\ f(x)=x^{3}\)
Dominio:\\(\ (-\infty, \infty)\)
intercepción x: (0, 0)
intercepción en Y: (0, 0)
impar
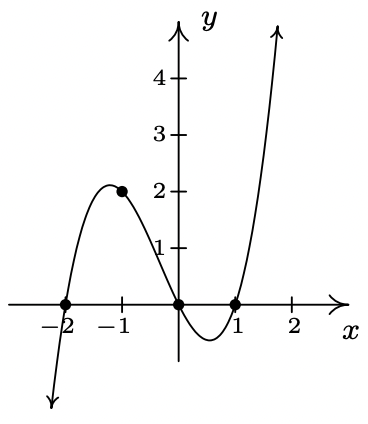
- \(\ f(x) = x(x − 1)(x + 2)\)
Dominio:\\(\ (-\infty, \infty)\)
x-intercepta: (−2, 0), (0, 0), (1, 0)
intercepción en Y: (0, 0)
Sin simetría
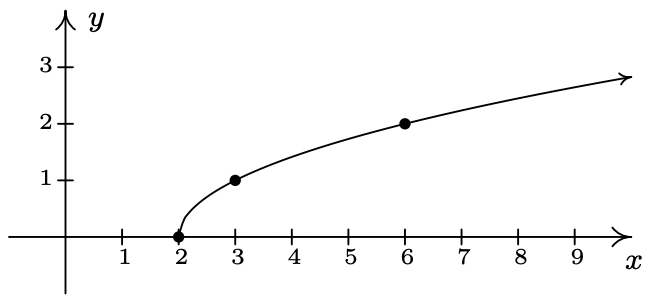
- \(\ f(x)=\sqrt{x-2}\)
Dominio:\(\[2, \infty)\)
intercepción x: (2, 0)
Intercepción en Y: Ninguna
Sin simetría
- \(\ f(x)=\sqrt{x-2}\)
Dominio:\(\[2, \infty)\)
intercepción x: (5, 0)
Intercepción en Y:\(\ (0, \sqrt{5})\)
Sin simetría
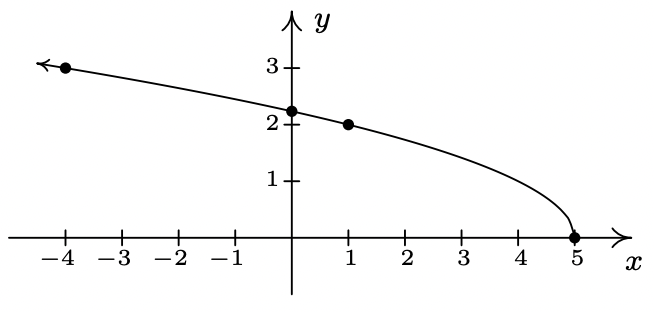
- \(\ f(x)=3-2 \sqrt{x+2}\)
Dominio:\(\ [-2, \infty)\)
X-intercepción:\(\ \left(\frac{1}{4}, 0\right)\)
Intercepción en Y:\(\ (0,3-2 \sqrt{2})\)
Sin simetría
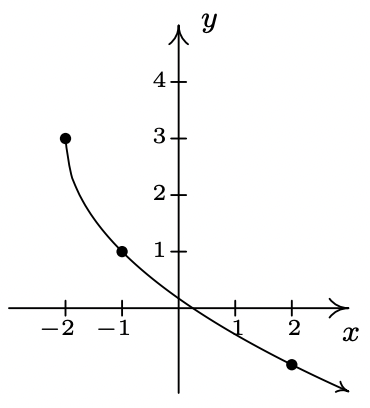
- \(\ f(x)=\sqrt[3]{x}\)
Dominio:\\(\ (-\infty, \infty)\)
intercepción x: (0, 0)
intercepción en Y: (0, 0)
impar
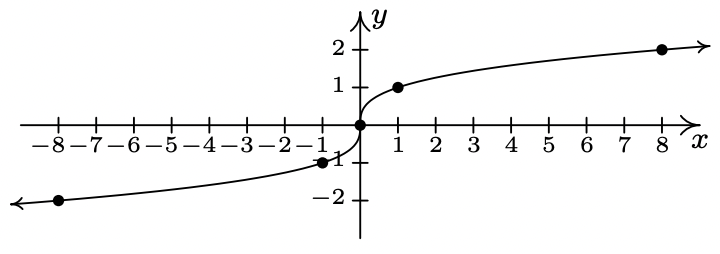
- \(\ f(x)=\frac{1}{x^{2}+1}\)
Dominio:\\(\ (-\infty, \infty)\)
x-intercept: Ninguno
intercepción en Y: (0, 1)
Incluso
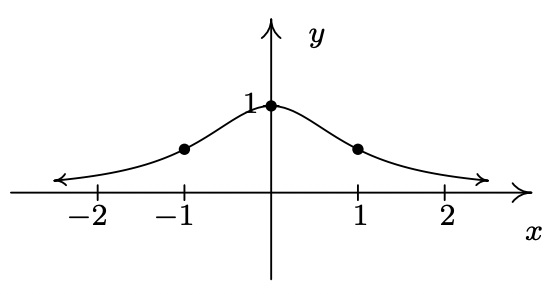
- impar
- ni
- incluso
- incluso
- incluso
- ni
- impar
- impar
- incluso
- ni
- ni
- incluso
- par e impar
- impar
- incluso
- incluso
- ni
- impar
- impar
- incluso
- incluso
- [−5, 3]
- [−5, 4]
- \(\ f(−2) = 2\)
- x = −3
- (−4, 0), (−1, 0), (1, 0)
- (0, −1)
- −4, −1, 1
- \(\ [-4,-1] \cup[1,3]\)
- 4
- ni
- [−5, −3], [0, 2]
- [−3, 0], [2, 3]
- \(\ f(−3) = 4, f(2) = 3\)
- \(\ f(0) = −1\)
- \(\ f(−3) = 4\)
- \(\ f(−5) = −5\)
- [−4, 4]
- [−5, 5)
- \(\ f(2) = 3\)
- x = −2
- (−4, 0), (0, 0), (4, 0)
- (0, 0)
- −4, 0, 4
- \(\ [-4,0] \cup\{4\}\)
- 3
- ni
- [−2, 2)
- [−4, −2], (2, 4]
- ninguno
- \(\ f(−2) = −5, f(2) = 3\)
- ninguno
- \(\ f(−2) = −5\)
- Sin máximo absoluto
Mínimo absoluto\(\ f(4.55) ≈ −175.46\)
Mínimo local en (−2.84, −91.32)
Máximo local en (0.54, 55.73)
Mínimo local en (4.55, −175.46)
Aumentando en [−2.84, 0.54], [4.55, ∞)
Disminuyendo el (−∞, −2.84], [0.54, 4.55]
- Sin máximo absoluto
Sin mínimo absoluto
Máximo local en (0, 0)
Mínimo local en (1.60, −3.28)
Aumentando el (−∞, 0], [1.60, ∞)
Disminuyendo el [0, 1.60]
- Máximo absoluto\(\ f(0) = 3\)
Mínimo absoluto f (±3) = 0
Máximo local en (0, 3)
Sin mínimo local
Aumentando en [−3, 0]
Disminuyendo el [0, 3]
- Máximo absoluto f (2.12) ≈ 4.50
Mínimo absoluto f (−2.12) ≈ −4.50
Máximo local (2.12, 4.50)
Mínimo local (−2.12, −4.50)
Aumentando en [−2.12, 2.12]
Disminuyendo el [−3, −2.12], [2.12, 3]
- \(\ (f + g)(0) = 4\)
- \(\ (f + g)(1) = 5\)
- \(\ (f − g)(1) = −1\)
- \(\ (g − f)(2) = 0\)
- \(\ (fg)(2) = 9\)
- \(\ (fg)(1) = 6\)
- \(\ \left(\frac{f}{g}\right)(4)=0\)
- \(\ \left(\frac{g}{f}\right)(2)=1\)
- \(\ h(0) = 2\), por lo que el Sasquatch mide 2 pies de altura al nacer.
- \(\ h(15) = 6\), por lo que la Saquatch mide 6 pies de altura cuando tiene 15 años.
- \(\ h(N) = 6\)cuándo\(\ N = 15\) y\(\ N = 60\). Esto significa que la Sasquatch mide 6 pies de altura cuando tiene 15 y 60 años de edad.
- \(\ h\)es constante en [30, 45]. Esto significa que la altura del Sasquatch es constante (a 8 pies) para estos años.
- \(\ h\)está disminuyendo el [45, 60]. Esto significa que el Sasquatch se está acortando desde los 45 años hasta los 60 años. (Sasquatchteoporosis, ¿quizás?)
- Tenga en cuenta que\(\ f(1.1) = 1\), pero\(\ f(−1.1) = −2\), así que f no es ni par ni impar.
Referencia
1 ¡Acabamos de entrar en Cálculo aquí!
2 ¿Por qué somos tan despectivos sobre la simetría sobre el eje x para las gráficas de funciones?
3 ¿Alguna idea?
4 'Sugiere' es sobre el alcance de lo que puede hacer.
5 ¡Consulta tu manual del propietario, instructor o sitio de videos favorito!
6 O, en otras palabras, ¡no confíes demasiado en la máquina!
7 En Cálculo se exploran las nociones de cuán rápido o lento aumenta o disminuye una función
8 También se llama 'máximo relativo'.
9 Lo haremos más preciso en un momento.
10 También se llama 'mínimo relativo'.
11 'Maxima' es el plural de 'máximo' y 'mimima' es el plural de 'mínimo'. 'Extrema' es el plural de 'extremum' que combina máximo y mínimo.
12 A veces llamado el máximo 'absoluto' o 'global'.
13 De nuevo, se puede utilizar el mínimo 'absoluto' o 'global'.
14 pero no prueba
15 Aunque, a decir verdad, sólo hay un paso de Cálculo involucrado, seguido de varias páginas de álgebra.
16 Parece tonto enumerar una respuesta final como (2.00, 1.00). En efecto, Cálculo confirma que la respuesta exacta a este problema es, de hecho, (2, 1). Como ya sabrás bien, los autores son demasiado pedantes, y como tal, utilizan los decimales para recordarle al lector que cualquier resultado obtenido de una calculadora de esta manera es una aproximación, y debe tratarse como tal.

