1.7: Transformaciones
- Page ID
- 119444
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
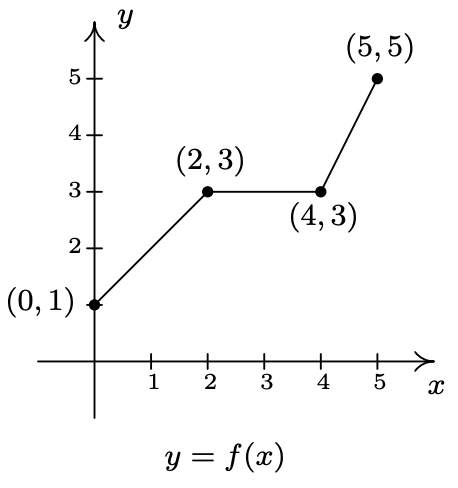
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección, estudiamos cómo las gráficas de funciones cambian, o se transforman, cuando se realizan ciertas modificaciones especializadas en sus fórmulas. Las transformaciones que estudiaremos se dividen en tres amplias categorías: turnos, reflexiones y escalaciones, y las presentaremos en ese orden. Supongamos que la gráfica a continuación es la gráfica completa de una función\(f\).
Figura\(\PageIndex{1}\)
El Principio Fundamental de Gráfica para Funciones dice que para que un punto\((a,b)\) esté en la gráfica,\(f(a) = b\). En particular, sabemos\(f(0) = 1\),\(f(2)=3\),\(f(4)=3\) y\(f(5)=5\). Supongamos que quisiéramos graficar la función definida por la fórmula\(g(x) = f(x) + 2\). Tomemos un minuto para recordarnos lo que\(g\) está haciendo. Comenzamos con una entrada\(x\) a la función\(f\) y obtenemos la salida\(f(x)\). La función\(g\) toma la salida\(f(x)\) y se suma\(2\) a ella. Para poder graficar\(g\), necesitamos graficar los puntos\((x,g(x))\). ¿Cómo vamos a encontrar los valores para\(g(x)\) sin una fórmula para\(f(x)\)? La respuesta es que no necesitamos una fórmula para\(f(x)\), solo necesitamos los valores de\(f(x)\). Los valores de\(f(x)\) son los\(y\) valores en la gráfica de\(y=f(x)\). Por ejemplo, utilizando los puntos indicados en la gráfica de\(f\), podemos hacer la siguiente tabla.
\(\begin{array}{|c||c|c|c|c|} \hline x & (x,f(x)) & f(x) & g(x)=f(x)+2 & (x, g(x)) \\ \hline 0 & (0,1)& 1 & 3 &(0, 3) \\ \hline 2 & (2,3) & 3 & 5 &(2,5) \\ \hline 4 & (4,3) & 3 & 5 &(4, 5) \\ \hline 5 & (5,5) & 5 & 7 &( 5 ,7) \\ \hline \end{array}\)
En general, si\((a,b)\) está en la gráfica de\(y=f(x)\), entonces\(f(a) = b\), así\(g(a) = f(a) +2 = b+2\). De ahí,\((a,b+2)\) está en la gráfica de\(g\). Es decir, para obtener la gráfica de\(g\), agregamos\(2\) a la\(y\) coordenada -de cada punto en la gráfica de\(f\). Geométricamente, la adición\(2\) a la\(y\) coordenada -de un punto mueve las\(2\) unidades de punto por encima de su ubicación anterior. Agregar\(2\) a cada\(y\) coordenada en una gráfica en masa se suele describir como 'desplazar la gráfica hacia arriba\(2\) unidades'. Observe que la gráfica conserva la misma forma básica que antes, es solo\(2\) unidades por encima de su ubicación original. Es decir, conectamos los cuatro puntos que movimos de la misma manera en que estaban conectados antes. Tenemos los resultados uno al lado del otro en la parte superior de la página siguiente.

Figura\(\PageIndex{1}\): Copy and Paste Caption here. (Copyright; author via source)
Notarás que el dominio de\(f\) y el dominio de\(g\) son los mismos, es decir\([0,5]\), pero que el rango de\(f\) es\([1,5]\) mientras el rango de\(g\) es\([3,7]\). En general, desplazar una función verticalmente así dejará el dominio sin cambios, pero muy bien podría afectar el rango. Se puede imaginar fácilmente lo que pasaría si quisiéramos graficar la función\(j(x) = f(x) - 2\). En lugar de\(2\) sumar a cada una de las\(y\) coordenadas -en la gráfica de\(f\), estaríamos restando\(2\). Geométricamente, estaríamos moviendo la gráfica hacia abajo\(2\) unidades. Dejamos al lector verificar que el dominio de\(j\) es el mismo que\(f\), pero el rango de\(j\) es\([-1,3]\). Lo que hemos discutido es generalizado en el siguiente teorema.
Supongamos que\(f\) es una función y\(k\) es un número positivo.
- Para graficar\(y=f(x)+k\), desplace la gráfica de\(k\) unidades\(y=f(x)\) hacia arriba sumando\(k\) a las\(y\) coordenadas -de los puntos en la gráfica de\(f\).
- Para graficar\(y=f(x)-k\), desplace la gráfica de\(k\) unidades\(y=f(x)\) descendentes restando\(k\) de las\(y\) coordenadas -de los puntos en la gráfica de\(f\).
La clave para entender el Teorema 1.2 y, de hecho, todos los teoremas de esta sección proviene de una comprensión del Principio Fundamental de Gráfica para Funciones. Si\((a,b)\) está en la gráfica de\(f\), entonces\(f(a) = b\). Sustituir\(x=a\) en la ecuación\(y=f(x)+k\) da\(y=f(a)+k = b+k\). De ahí,\((a,b+k)\) está en la gráfica de\(y=f(x)+k\), y tenemos el resultado. En el lenguaje de 'entradas' y 'salidas', el Teorema 1.2 puede parafrasearse como “Agregar a, o restar de, la salida de una función hace que la gráfica se desplace hacia arriba o hacia abajo, respectivamente”. Entonces, ¿qué pasa si sumamos o restamos de la entrada de la función?
Siguiendo con la gráfica de\(y=f(x)\) arriba, supongamos que queríamos graficar\(g(x) = f(x+2)\). En otras palabras, estamos buscando ver qué sucede cuando agregamos\(2\) a la entrada de la función. 1 Intentemos generar una tabla de valores de\(g\) basados en los que conocemos\(f\). Rápidamente encontramos que nos encontramos con algunas dificultades.
\[\begin{array}{|c||c|c|c|c|} \hline x & (x,f(x)) & f(x)& g(x)=f(x+2) & (x, g(x)) \\ \hline 0 & (0,1)& 1 & f(0+2) = f(2) = 3 &(0, 3) \\ \hline 2 & (2,3) & 3 & f(2+2) = f(4) = 3 &(2,3) \\ \hline 4 & (4,3) & 3 & f(4+2) = f(6) = ? & \\ \hline 5 & (5,5) & 5 & f(5+2) = f(7) = ? & \\ \hline \end{array}\]
Cuando sustituimos\(x=4\) en la fórmula\(g(x)=f(x+2)\), se nos pide encontrar\(f(4+2)=f(6)\) cuál no existe porque el dominio de\(f\) es solo\([0,5]\). Lo mismo sucede cuando intentamos encontrar\(g(5)\). Lo que necesitamos aquí es una nueva estrategia. Sabemos, por ejemplo,\(f(0) = 1\). Para determinar el punto correspondiente en la gráfica de\(g\), necesitamos averiguar en qué valor\(x\) debemos sustituir\(g(x) = f(x+2)\) para que la cantidad\(x+2\), resulte ser\(0\). Resolver\(x+2=0\) da\(x=-2\), y\(g(-2) = f((-2)+2) = f(0) = 1\) así\((-2,1)\) está en la gráfica de\(g\). Para usar el hecho\(f(2) = 3\), nos pusimos\(x+2 = 2\) a conseguir\(x=0\). Sustituyendo da\(g(0) = f(0+2) = f(2) = 3\). Continuando con esta moda, obtenemos\[\begin{array}{|r||c|c|c|} \hline x & x+2 & g(x)=f(x+2) & (x, g(x)) \\ \hline -2 & 0 & g(-2)=f(0) = 1 &(-2, 1) \\ \hline 0 & 2 & g(0)=f(2) = 3 &(0,3) \\ \hline 2 & 4 & g(2)=f(4) = 3 & (2,3)\\ \hline 3 & 5 & g(3)=f(5) = 5 & (3,5) \\ \hline \end{array}\]
En resumen, los puntos\((0,1)\),\((2,3)\),\((4,3)\) y\((5,5)\) en la gráfica de\(y=f(x)\) dan lugar a los puntos\((-2,1)\),\((0,3)\),\((2,3)\) y\((3,5)\) en la gráfica de\(y=g(x)\), respectivamente. En general, si\((a,b)\) está en la gráfica de\(y=f(x)\), entonces\(f(a) = b\). Resolver\(x+2 = a\) da\(x = a-2\) para que\(g(a-2) = f((a-2)+2) = f(a) = b\). Como tal,\((a-2,b)\) está en la gráfica de\(y=g(x)\). El punto\((a-2,b)\) es exactamente\(2\) unidades a la izquierda del punto por\((a,b)\) lo que la gráfica de\(y=g(x)\) se obtiene desplazando la gráfica\(y=f(x)\) a las\(2\) unidades de la izquierda, como se muestra a continuación.

Figura\(\PageIndex{1}\)
Tenga en cuenta que si bien los rangos de\(f\) y\(g\) son los mismos, el dominio de\(g\) es\([-2,3]\) mientras que el dominio de\(f\) es\([0,5]\). En general, cuando desplazamos la gráfica horizontalmente, el rango seguirá siendo el mismo, pero el dominio podría cambiar. Si nos propusiéramos graficar\(j(x) = f(x-2)\), nos encontraríamos sumando\(2\) a todos los\(x\) valores de los puntos en la gráfica de\(y=f(x)\) para efectuar un desplazamiento a las\(2\) unidades correctas. Generalizar estas nociones produce el siguiente resultado.
Supongamos que\(f\) es una función y\(h\) es un número positivo.
- Para graficar\(y=f(x+h)\), desplace la gráfica de\(h\) unidades\(y=f(x)\) izquierdas restando\(h\) de las\(x\) coordenadas -de los puntos en la gráfica de\(f\).
- Para graficar\(y=f(x-h)\), desplace la gráfica de\(h\) unidades\(y=f(x)\) derechas sumando\(h\) a las\(x\) coordenadas -de los puntos en la gráfica de\(f\).
En otras palabras, el Teorema 1.3 dice que sumar o restar de la entrada a una función equivale a desplazar la gráfica a la izquierda o a la derecha, respectivamente. Teorema 1.3 y Teorema 1.3 presentan un tema que se ejecutará común a lo largo de la sección: los cambios a las salidas de una función afectan a las\(y\) -coordenadas de la gráfica, resultando en algún tipo de cambio vertical; los cambios en las entradas a una función afectan al\(x\) - coordenadas de la gráfica, resultando en algún tipo de cambio horizontal.
- Gráfica\(f(x) = \sqrt{x}\). Trazar al menos tres puntos.
- Usa tu gráfica en 1 para graficar\(g(x) = \sqrt{x}-1\).
- Usa tu gráfica en 1 para graficar\(j(x) = \sqrt{x-1}\).
- Usa tu gráfica en 1 para graficar\(m(x) = \sqrt{x+3} - 2\).
Solución.
- Debido a la raíz cuadrada, el dominio de\(f\) is\(x \geq 0\), o\([0,\infty)\). Elegimos cuadrados perfectos para construir nuestra tabla y gráfica a continuación. A partir de la gráfica verificamos el dominio de\(f\) es\([0,\infty)\) y el rango de\(f\) es también\([0, \infty)\).
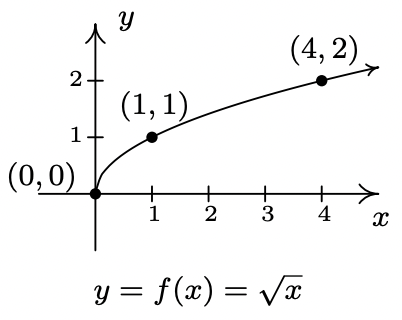
\(\begin{array}{|c||c|c|} \hline x & f(x) & (x,f(x)) \\ \hline 0 & 0& (0,0) \\ \hline 1 & 1 & (1,1) \\ \hline 4 & 2 & (4,2) \\ \hline \end{array}\)&
-1 5 -1 3 (-1,0.25)\((0,0)\) (1,1.5)\((1,1)\) (4,2.5)\((4,2)\) (5, -0.5)\(x\) (0.5,3)\(y\)
- El dominio de\(g\) es el mismo que el dominio de\(f\), ya que la única condición en ambas funciones es esa\(x \geq 0\). Si comparamos la fórmula para\(g(x)\) con\(f(x)\), vemos eso\(g(x) = f(x) - 1\). En otras palabras, hemos restado\(1\) de la salida de la función\(f\). Por Teorema 1.2, sabemos que para poder graficar\(g\), desplazamos la gráfica de\(f\) abajo una unidad restando\(1\) de cada una de las\(y\) -coordenadas de los puntos en la gráfica de\(f\). Aplicando esto a los tres puntos que hemos especificado en la gráfica, pasamos\((0,0)\) a\((0,-1)\),\((1,1)\) a\((1,0)\), y\((4,2)\) a\((4,1)\). El resto de los puntos siguen su ejemplo, y los conectamos con la misma forma básica que antes. Confirmamos el dominio de\(g\) es\([0, \infty)\) y encontramos el rango\(g\) de ser\([-1, \infty)\).

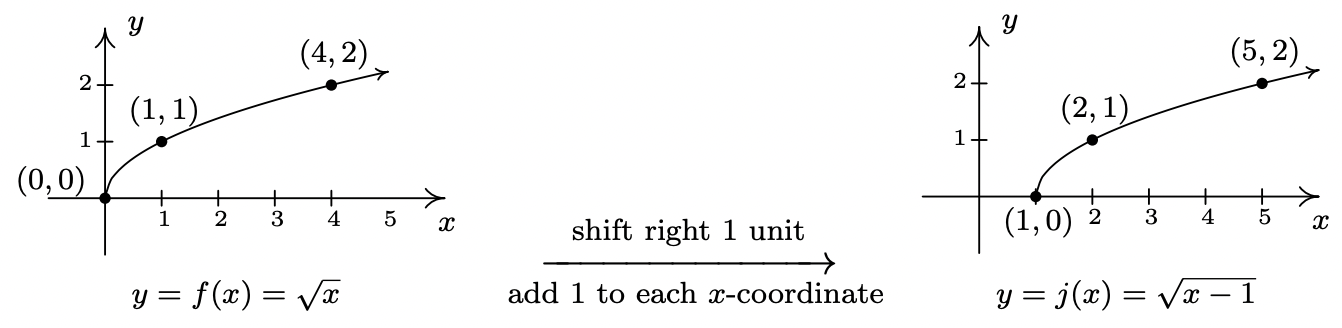
- Resolver\(x-1 \geq 0\) da\(x \geq 1\), por lo que el dominio de\(j\) es\([1,\infty)\). Para graficar\(j\), notamos eso\(j(x) = f(x-1)\). En otras palabras, estamos restando\(1\) de la entrada de\(f\). Según el Teorema 1.3, esto induce un desplazamiento a la derecha de la gráfica de\(f\). Agregamos\(1\) a las\(x\) -coordenadas de los puntos en la gráfica de\(f\) y obtenemos el resultado a continuación. El gráfico reafirma que el dominio de\(j\) es\([1,\infty)\) y nos dice que el rango de\(j\) es\([0,\infty)\).
- Para encontrar el dominio de\(m\), resolvemos\(x+3 \geq 0\) y obtenemos\([-3, \infty)\). Comparando las fórmulas de\(f(x)\) y\(m(x)\), tenemos\(m(x) = f(x+3) - 2\). Nos hemos\(3\) sumado a una entrada, indicando un desplazamiento horizontal, y\(2\) siendo restados de una salida, indicando un desplazamiento vertical. Dejamos al lector verificar que, en este caso particular, el orden en que realizamos estas transformaciones es inmaterial; llegaremos a la misma gráfica independientemente de a qué transformación apliquemos primero. 2 Seguimos la convención 'insumos primero', 3 y para ello abordamos primero el cambio horizontal. Dejando\(m_{1}(x) = f(x+3)\) denotar este paso intermedio, el Teorema 1.3 nos dice que la gráfica de\(y=m_{1}(x)\) es la gráfica de\(f\) desplazada a las\(3\) unidades de la izquierda. De ahí que restemos\(3\) de cada una de las\(x\) -coordenadas de los puntos en la gráfica de\(f\).
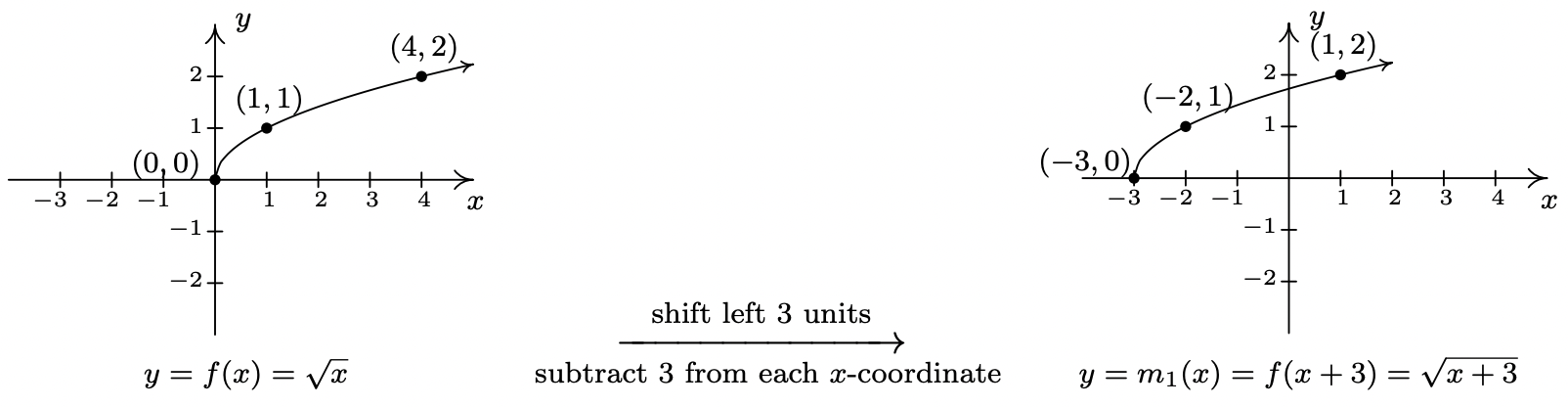
Desde\(m(x) = f(x+3)-2\) y\(f(x+3) = m_{1}(x)\), tenemos\(m(x) = m_{1}(x) - 2\). Podemos aplicar el Teorema 1.2 y obtener la gráfica de\(m\) restando\(2\) de las\(y\) -coordenadas de cada uno de los puntos en la gráfica de\(m_{1}(x)\). La gráfica verifica que el dominio de\(m\) es\([-3, \infty)\) y encontramos el rango de\(m\) ser\([-2, \infty)\).
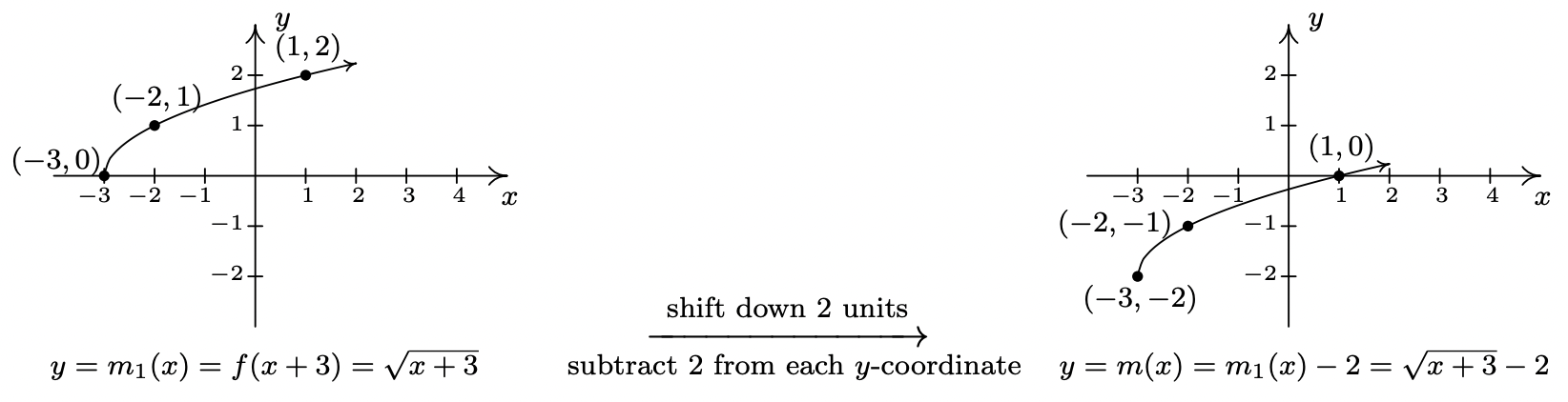
Tenga en cuenta que podemos verificar nuestra respuesta a cualquiera de estos tipos de problemas demostrando que cualquiera de los puntos que hemos movido se encuentra en la gráfica de nuestra respuesta final. Por ejemplo, podemos comprobar que\((-3,-2)\) está en la gráfica de\(m\) por computación\(m(-3) = \sqrt{(-3)+3} - 2 = \sqrt{0}-2 = -2\, \checkmark\)
Ahora volvemos nuestra atención a las reflexiones. Sabemos por la Sección 1.1 que para reflejar un punto\((x,y)\) a través del\(x\) eje,\(y\) reemplazamos por\(-y\). Si\((x,y)\) está en la gráfica de\(f\), entonces\(y=f(x)\), entonces reemplazar\(y\) con\(-y\) es lo mismo que reemplazar\(f(x)\) con\(-f(x)\). De ahí que la gráfica de\(y=-f(x)\) sea la gráfica de\(f\) reflejada a través del\(x\) eje. De igual manera, la gráfica de\(y=f(-x)\) es la gráfica de\(f\) reflejada a través del\(y\) eje. Volviendo al lenguaje de entradas y salidas, multiplicando la salida de una función por\(-1\) refleja su gráfica a través del\(x\) eje, mientras que multiplicar la entrada a una función por\(-1\) refleja la gráfica a través del\(y\) eje. 4
Supongamos que\(f\) es una función.
- Para graficar\(y=-f(x)\), refleje la gráfica de\(y=f(x)\) a través\(x\) del eje -multiplicando las\(y\) coordenadas -de los puntos en la gráfica de\(f\) por\(-1\).
- Para graficar\(y=f(-x)\), refleje la gráfica de\(y=f(x)\) a través\(y\) del eje -multiplicando las\(x\) coordenadas -de los puntos en la gráfica de\(f\) por\(-1\).
Aplicando el Teorema 1.4 a la gráfica de\(y=f(x)\) dado al inicio de la sección, podemos graficar\(y=-f(x)\) reflejando la gráfica de\(f\) alrededor del\(x\) eje -eje

Al reflejar la gráfica de\(f\) a través del\(y\) eje, obtenemos la gráfica de\(y=f(-x)\).

Con la adición de reflexiones, ahora es más importante que nunca considerar el orden de las transformaciones, como ilustra el siguiente ejemplo.
Vamos\(f(x) = \sqrt{x}\). Utilice la gráfica\(f\) del Ejemplo 1.7.1 para graficar las siguientes funciones. También, exponer sus dominios y rangos.
- \(g(x) = \sqrt{-x}\)
- \(j(x) = \sqrt{3-x}\)
- \(m(x) = 3 - \sqrt{x}\)
Solución.
- La mera visión de\(\sqrt{-x}\) suele provocar alarma, si no pánico. Cuando discutimos dominios en la Sección 1.4, claramente desterramos los negativos de los radicandos de raíces pares. No obstante, debemos recordar que\(x\) es una variable, y como tal, la cantidad\(-x\) no siempre es negativa. Por ejemplo, si\(x=-4\),\(-x = 4\), así\(\sqrt{-x} = \sqrt{-(-4)} = 2\) está perfectamente bien definido. Para encontrar el dominio analíticamente, establecemos\(-x \geq 0\) cuál da\(x \leq 0\), para que el dominio de\(g\) sea\((-\infty, 0]\). Ya que\(g(x) = f(-x)\), el Teorema 1.4 nos dice que la gráfica de\(g\) es el reflejo de la gráfica de\(f\) a través del\(y\) eje -eje. Logramos esto multiplicando cada\(x\) coordenada en la gráfica de\(f\) por\(-1\), de manera que los puntos\((0,0)\),\((1,1)\), y\((4,2)\) se mueven a\((0,0)\)\((-1,1)\), y\((-4,2)\), respectivamente. Gráficamente, vemos que el dominio de\(g\) es\((-\infty, 0]\) y el rango de\(g\) es el mismo que el rango de\(f\), es decir\([0,\infty)\).

- Para determinar el dominio de\(j(x) = \sqrt{3-x}\), resolvemos\(3-x \geq 0\) y obtenemos\(x \leq 3\), o\((-\infty, 3]\). Para determinar qué transformaciones necesitamos aplicar a la gráfica de\(f\) para obtener la gráfica de\(j\), reescribimos\(j(x) = \sqrt{-x+3} = f(-x+3)\). Comparando esta fórmula con\(f(x) = \sqrt{x}\), vemos que no sólo estamos multiplicando la entrada\(x\) por\(-1\), lo que da como resultado una reflexión a través del\(y\) eje -eje, sino que también estamos sumando\(3\), lo que indica un desplazamiento horizontal hacia la izquierda. ¿Importa en qué orden hacemos las transformaciones? Si es así, ¿cuál es el orden correcto? Consideremos el punto\((4,2)\) en la gráfica de\(f\). Nos referimos a la discusión previa al Teorema 1.3. Conocemos\(f(4) = 2\) y deseamos encontrar el punto sobre el\(y=j(x) = f(-x+3)\) que corresponde\((4,2)\). Fijamos\(-x+3 = 4\) y resolvemos. Nuestro primer paso es restar\(3\) de ambos lados para conseguir\(-x=1\). Restar\(3\) de la\(x\) coordenada\(4\) -es desplazar el punto\((4,2)\) hacia la izquierda. De\(-x=1\), luego multiplicamos 5 ambos lados por\(-1\) para conseguir\(x=-1\). Multiplicar la\(x\) coordenada -por\(-1\) corresponde a reflejar el punto alrededor del\(y\) eje -eje. De ahí que primero realizamos el desplazamiento horizontal, luego lo seguimos con la reflexión alrededor del\(y\) eje. Empezando por\(f(x) = \sqrt{x}\), dejamos\(j_{1}(x)\) ser la función intermedia que desplaza la gráfica de\(f\)\(3\) unidades hacia la izquierda,\(j_{1}(x) = f(x+3)\).

Para obtener la función\(j\), reflejamos la gráfica de\(j_{1}\) aproximadamente\(y\) -eje. El teorema 1.4 nos dice que tenemos\(j(x) = j_{1}(-x)\). Armando todo, tenemos\(j(x) = j_{1}(-x) = f(-x+3) = \sqrt{-x+3}\), que es lo que queremos. 6 A partir de la gráfica, confirmamos el dominio de\(j\) es\((-\infty, 3]\) y obtenemos que el rango es\([0, \infty)\).

- El dominio de\(m\) funciona para ser el dominio de\(f\),\([0, \infty)\). Reescribiendo\(m(x) = -\sqrt{x} + 3\), vemos\(m(x) = -f(x) + 3\). Como estamos multiplicando la salida de\(f\) por\(-1\) y luego sumando\(3\), nuevamente tenemos dos transformaciones que enfrentar: una reflexión a través del\(x\) eje y un desplazamiento vertical. Para determinar el orden correcto en el que aplicar las transformaciones, nos imaginamos tratando de determinar el punto en la gráfica del\(m\) cual corresponde a\((4,2)\) en la gráfica de\(f\). Ya que en la fórmula para\(m(x)\), la entrada a\(f\) es justa\(x\), sustituimos para encontrar\(m(4) = -f(4)+3 = -2+3=1\). De ahí,\((4,1)\) es el punto correspondiente en la gráfica de\(m\). Si examinamos de cerca la aritmética, vemos que primero multiplicamos\(f(4)\) por\(-1\), lo que corresponde a la reflexión a través\(x\) del eje -y luego sumamos\(3\), que corresponde al desplazamiento vertical. Si definimos una función intermedia\(m_{1}(x) = -f(x)\) para cuidar la reflexión, obtenemos

Para desplazar la gráfica de\(3\) unidades\(m_{1}\) ascendentes, establecemos\(m(x) = m_{1}(x)+3\). Ya que\(m_{1}(x) = -f(x)\), cuando lo armamos todo, obtenemos\(m(x) = m_{1}(x)+3 = -f(x) + 3 = -\sqrt{x}+3\). Vemos por la gráfica que el rango de\(m\) es\((-\infty, 3]\).

Ahora dirigimos nuestra atención a nuestra última clase de transformaciones conocidas como escalamientos. Una discusión a fondo sobre las escalaciones puede complicarse porque no son tan sencillas como las transformaciones anteriores. Una revisión rápida de lo que hemos cubierto hasta ahora, es decir, los desplazamientos verticales, los desplazamientos horizontales y las reflexiones, le mostrará por qué esas transformaciones se conocen como transformaciones rígidas. En pocas palabras, no cambian la forma de la gráfica, solo su posición y orientación en el plano. Sin embargo, si quisiéramos hacer una nueva gráfica dos veces más alta que una gráfica dada, o un tercio de ancho, estaríamos cambiando la forma de la gráfica. Este tipo de transformación se llama no rígida por razones obvias. No sólo será importante para nosotros diferenciar entre la modificación de entradas versus salidas, también debemos prestar mucha atención a la magnitud de los cambios que hagamos. Como verás en breve, la Matemática resulta ser más fácil que la gramática asociada.
Supongamos que queremos graficar la función\(g(x) =2 f(x)\) donde\(f(x)\) está la función cuya gráfica se da al inicio de la sección. A partir de su gráfica, podemos construir una tabla de valores para\(g\) como antes.
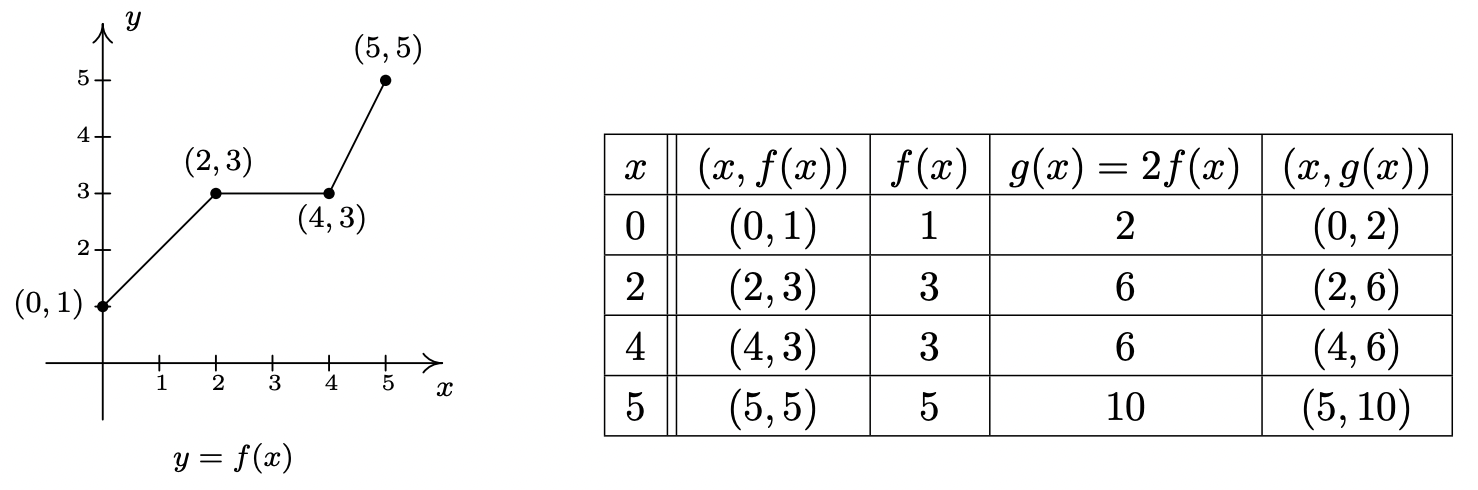
Figura\(\PageIndex{1}\)
En general, si\((a,b)\) está en la gráfica de\(f\), entonces\(f(a) = b\) así que eso\(g(a) = 2 f(a) = 2b\) pone\((a,2b)\) en la gráfica de\(g\). Es decir, para obtener la gráfica de\(g\), multiplicamos todas las\(y\) -coordenadas de los puntos en la gráfica de\(f\) por\(2\). Multiplicando todas las\(y\) coordenadas de todos los puntos en la gráfica de\(f\) por\(2\) causas lo que se conoce como 'escalado vertical 7 por un factor de\(2\) ', y los resultados se dan en la página siguiente.
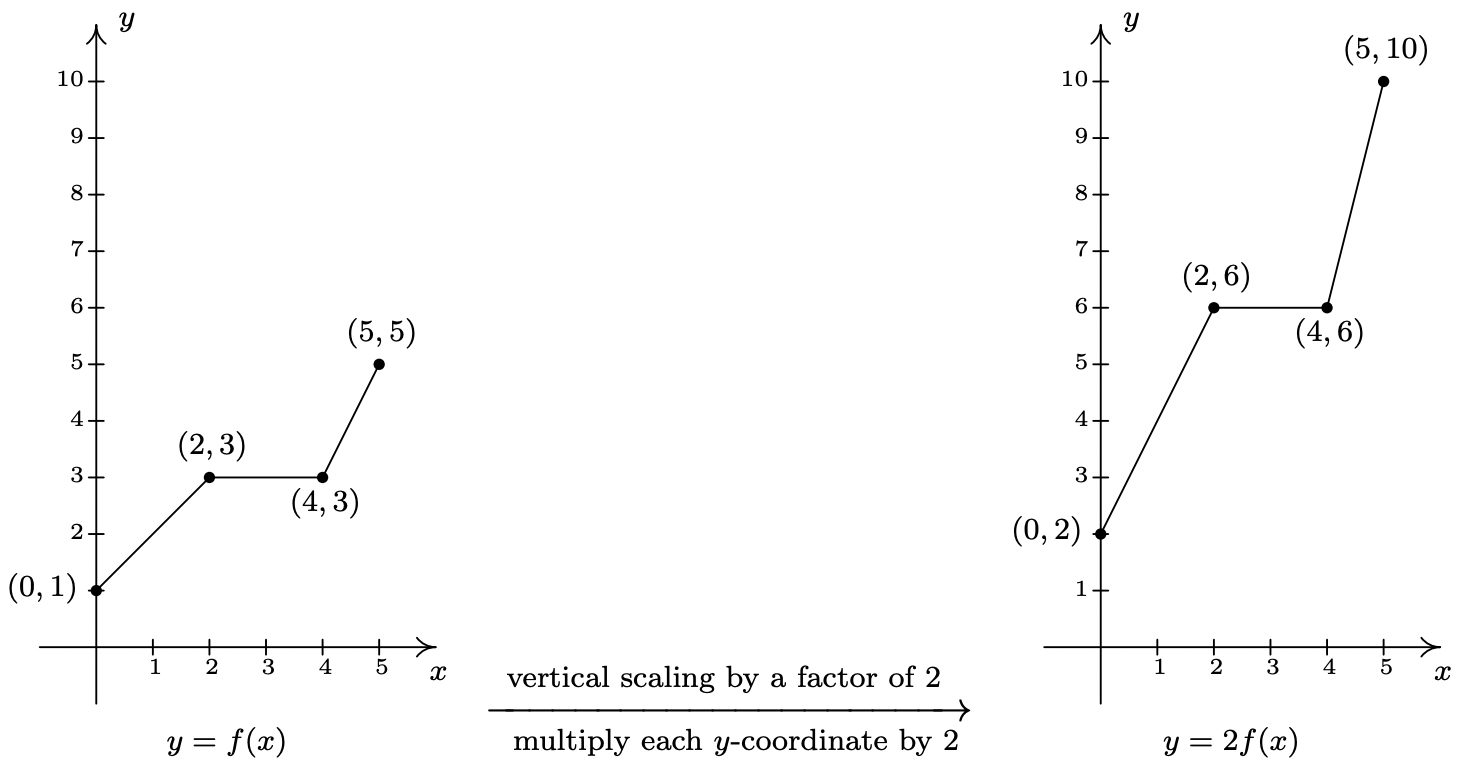
Si queremos graficar\(y = \frac{1}{2} f(x)\), multiplicamos todas las\(y\) coordenadas de los puntos en la gráfica de\(f\) por\(\frac{1}{2}\). Esto crea un 'escalado vertical 8 por un factor de\(\frac{1}{2}\) 'como se ve a continuación.

Estos resultados se generalizan en el siguiente teorema.
Supongamos que\(f\) es una función y\(a>0\). Para graficar\(y=a f(x)\), multiplique todas las\(y\) coordenadas -de los puntos en la gráfica de\(f\) por\(a\). Decimos que la gráfica de\(f\) ha sido escalada verticalmente por un factor de\(a\).
- Si\(a > 1\), decimos que la gráfica de\(f\) ha sufrido un estiramiento vertical (expansión, dilatación) por un factor de\(a\).
- Si\(0 < a < 1\), decimos que la gráfica de\(f\) ha sufrido una contracción vertical (compresión, contracción) por un factor de\(\frac{1}{a}\).
Algunos comentarios sobre el Teorema 1.5 están en orden. Primero, una nota sobre la verborrea. Para los autores, las palabras 'estiramiento', 'expansión' y 'dilatación' indican que algo se está haciendo más grande. De ahí que 'estirado por un factor\(2\) de' tenga sentido si estamos escalando algo multiplicándolo por\(2\). De igual manera, creemos que palabras como 'encogimiento', 'compresión' y 'contracción' indican que algo se está haciendo más pequeño, así que si escalamos algo por un factor de\(\frac{1}{2}\), diríamos que 'se encoge por un factor de\(2\) '- no 'se encoge por un factor de\(\frac{1}{2}\)'. Es por ello que hemos escrito las descripciones 'estiramiento por un factor\(a\) de' y 'encogiendo por un factor de\(\frac{1}{a}\) 'en el enunciado del teorema. Segundo, en términos de entradas y salidas, el Teorema 1.5 dice multiplicar las salidas de una función por número positivo\(a\) hace que la gráfica se escale verticalmente por un factor de\(a\). Es natural preguntarse qué pasaría si multiplicamos las entradas de una función por un número positivo. Esto nos lleva a nuestra última transformación de la sección.
Haciendo referencia a la gráfica de\(f\) dada al inicio de esta sección, supongamos que queremos graficar\(g(x) = f(2x)\). Es decir, estamos buscando ver qué efecto\(2\) tiene multiplicar las entradas a\(f\) por en su gráfica. Si intentamos construir una mesa directamente, rápidamente nos encontramos con el mismo problema que tuvimos en nuestra discusión previa al Teorema 1.3, como se ve en la tabla de la izquierda de abajo. Resolvemos este problema de la misma manera que antes resolvimos este problema. Por ejemplo, si queremos determinar el punto sobre el\(g\) que corresponde al punto\((2,3)\) en la gráfica de\(f\), establecemos\(2x =2\) así que\(x=1\). Sustituyendo\(x=1\) en\(g(x)\), obtenemos\(g(1) = f(2 \cdot 1) = f(2) = 3\), así que\((1,3)\) está en la gráfica de\(g\). Continuando de esta manera, obtenemos la mesa en la parte inferior derecha.
\ (\\ begin {alineado}
&\ begin {array} {|c||c|c|c|c|}
\ hline x & (x, f (x)) & f (x) & g (x) =f (2 x) & (x, g (x))\
\ hline 0 & (0,1) & 1 & f (2\ cdot 0) =f (0) =1 & (0,1)\\
\ hline 2 & (2,3) & 3 & f (2\ cdot 2) =f (4) =3 & amp; (2,3)\\
\ hline 4 & (4,3) & 3 & f (2\ cdot 4) =f (8) =? &\\
\ hline 5 & (5,5) & 5 & f (2\ cdot 5) =f (10) =? &\\
\ hline
\ end {array}\\
&\ begin {array} {|c||c|c|c|}
\ hline x & 2 x & g (x) =f (2 x) & (x, g (x))\
\ hline 0 & 0 & g (0) =f (0) =1 & (0,0)\
\ hline 1 & 2 & g (1) =f (2) =3 & (1,3)\\
\ hline 2 & 4 & g (2) =f (4) =3 & (2,3)\
\ hline\ frac {5} {2} & 5 & g\ left (\ frac {5} {2}\ derecha) =f (5) =5 &\ izquierda (\ frac {5} {2}, 5\ derecha)\
\ hline
\ end {array}
\ end {alineada}\)
En general, si\((a,b)\) está en la gráfica de\(f\), entonces\(f(a) = b\). De ahí que\(g\left(\frac{a}{2}\right) = f\left(2 \cdot \frac{a}{2}\right) = f(a) = b\) así\(\left(\frac{a}{2}, b\right)\) esté en la gráfica de\(g\). En otras palabras, para graficar\(g\) dividimos las\(x\) -coordenadas de los puntos en la gráfica de\(f\) por\(2\). Esto da como resultado una escala horizontal 9 por un factor de\(\frac{1}{2}\).

Si, por otro lado, queremos graficar\(y = f\left( \frac{1}{2} x\right)\), terminamos multiplicando las\(x\) -coordenadas de los puntos en la gráfica de\(f\) por\(2\) lo que resulta en una escala horizontal 10 por un factor de\(2\), como se demuestra a continuación.

Tenemos el siguiente teorema.
Supongamos que\(f\) es una función y\(b>0\). Para graficar\(y= f(bx)\), divida todas las\(x\) -coordenadas de los puntos en la gráfica de\(f\) por\(b\). Decimos que la gráfica de\(f\) ha sido escalada horizontalmente por un factor de\(\frac{1}{b}\).
- Si\(0 < b < 1\), decimos que la gráfica de\(f\) ha sufrido un estiramiento horizontal (expansión, dilatación) por un factor de\(\frac{1}{b}\).
- Si\(b>1\), decimos que la gráfica de\(f\) ha sufrido una contracción horizontal (compresión, contracción) por un factor de\(b\).
El teorema 1.6 nos dice que si multiplicamos la entrada a una función por\(b\), la gráfica resultante se escala horizontalmente por un factor de\(\frac{1}{b}\) ya que los\(x\) -valores se dividen por\(b\) para producir puntos correspondientes en la gráfica de\(y = f(bx)\). El siguiente ejemplo explora cómo las escalaciones verticales y horizontales interactúan a veces entre sí y con las otras transformaciones introducidas en esta sección.
Vamos\(f(x)= \sqrt{x}\). Utilice la gráfica\(f\) del Ejemplo 1.7.1 para graficar las siguientes funciones. También, exponer sus dominios y rangos.
- \(g(x) = 3 \sqrt{x}\)
- \(j(x) = \sqrt{9x}\)
- \(m(x) =1 - \sqrt{\frac{x+3}{2}}\)
Solución.
- Primero observamos que el dominio de\(g\) es\([0, \infty)\) por la razón habitual. A continuación, tenemos\(g(x) = 3 f(x)\) así por Teorema 1.5, obtenemos la gráfica de\(g\) multiplicando todas las\(y\) -coordenadas de los puntos en la gráfica de\(f\) por\(3\). El resultado es una escala vertical de la gráfica de\(f\) por un factor de\(3\). Encontramos la gama de\(g\) es también\([0, \infty)\).

- Para determinar el dominio de\(j\), resolvemos\(9x \geq 0\) encontrar\(x \geq 0\). Nuestro dominio es una vez más\([0,\infty)\). Reconocemos\(j(x) = f(9x)\) y por Teorema 1.6, obtenemos la gráfica de\(j\) dividiendo las\(x\) -coordenadas de los puntos en la gráfica de\(f\) por\(9\). De la gráfica, vemos el rango de\(j\) es también\([0,\infty)\).

- Resolver\(\frac{x+3}{2} \geq 0\) da\(x \geq -3\), por lo que el dominio de\(m\) es\([-3, \infty)\). Para aprovechar lo que sabemos de las transformaciones, reescribimos\(m(x) = - \sqrt{\frac{1}{2} x + \frac{3}{2}} + 1\), o\(m(x) =- f\left(\frac{1}{2} x + \frac{3}{2}\right) + 1\). Centrándonos primero en las entradas, observamos que la entrada a\(f\) en la fórmula para\(m(x)\) es\(\frac{1}{2} x + \frac{3}{2}\). Multiplicar el\(x\) por\(\frac{1}{2}\) corresponde a un estiramiento horizontal por un factor de\(2\), y sumar el\(\frac{3}{2}\) corresponde a un desplazamiento a la izquierda por\(\frac{3}{2}\). Como antes, resolvemos cuál realizar primero pensando en cómo encontraríamos el punto en\(m\) corresponder a un punto sobre\(f\), en este caso,\((4,2)\). Para usar\(f(4) = 2\), resolvemos\(\frac{1}{2} x + \frac{3}{2} = 4\). Nuestro primer paso es restar el\(\frac{3}{2}\) (el desplazamiento horizontal) para obtener\(\frac{1}{2} x = \frac{5}{2}\). A continuación, multiplicamos por\(2\) (el estiramiento horizontal) y obtenemos\(x = 5\). Definimos dos funciones intermedias para manejar primero el turno, luego el estiramiento. De acuerdo con el Teorema 1.3,\(m_{1}(x) = f\left(x+ \frac{3}{2}\right) = \sqrt{x+\frac{3}{2}}\) desplazará la gráfica de\(f\) a las\(\frac{3}{2}\) unidades de la izquierda.
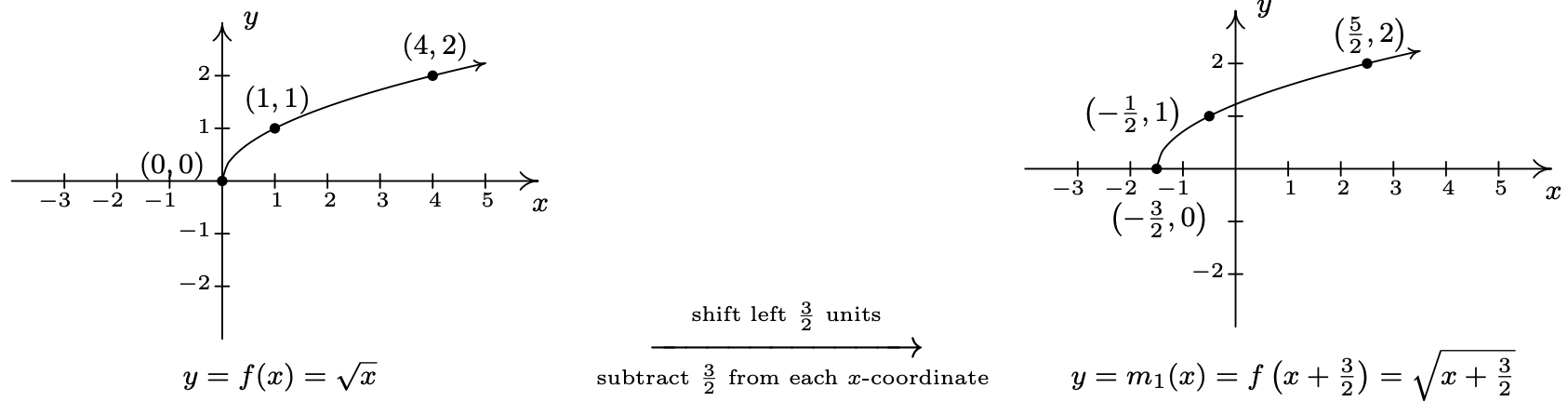
A continuación,\(m_{2}(x) = m_{1}\left(\frac{1}{2} x\right) = \sqrt{\frac{1}{2} x + \frac{3}{2}}\) se, según el Teorema 1.6, estirará horizontalmente la gráfica de\(m_{1}\) por un factor de\(2\).

Ahora examinamos lo que está sucediendo con los resultados. A partir de\(m(x) = - f\left(\frac{1}{2} x + \frac{3}{2}\right) + 1\), vemos que la salida de\(f\) se está multiplicando por\(-1\) (una reflexión alrededor del\(x\) eje -) y luego\(1\) se agrega a (un desplazamiento vertical hacia arriba\(1\)). Como antes, podemos determinar el orden correcto observando cómo\((4,2)\) se mueve el punto. Ya sabemos que para hacer uso de la ecuación\(f(4)=2\), necesitamos sustituirla\(x=5\). Obtenemos\(m(5) = - f\left(\frac{1}{2} (5) + \frac{3}{2}\right) + 1= - f(4)+1 = -2+1 = -1\). Vemos que\(f(4)\) (la salida de\(f\)) primero se multiplica por\(-1\) luego\(1\) se agrega lo que significa que primero reflejamos la gráfica sobre el\(x\) eje -luego desplazamos hacia arriba\(1\). El teorema 1.4 nos dice\(m_{3}(x) = - m_{2}(x)\) que manejará la reflexión.

Por último, para manejar el desplazamiento vertical, el Teorema 1.2 da\(m(x) = m_{3}(x) +1\), y vemos que el rango de\(m\) es\((-\infty,1]\).
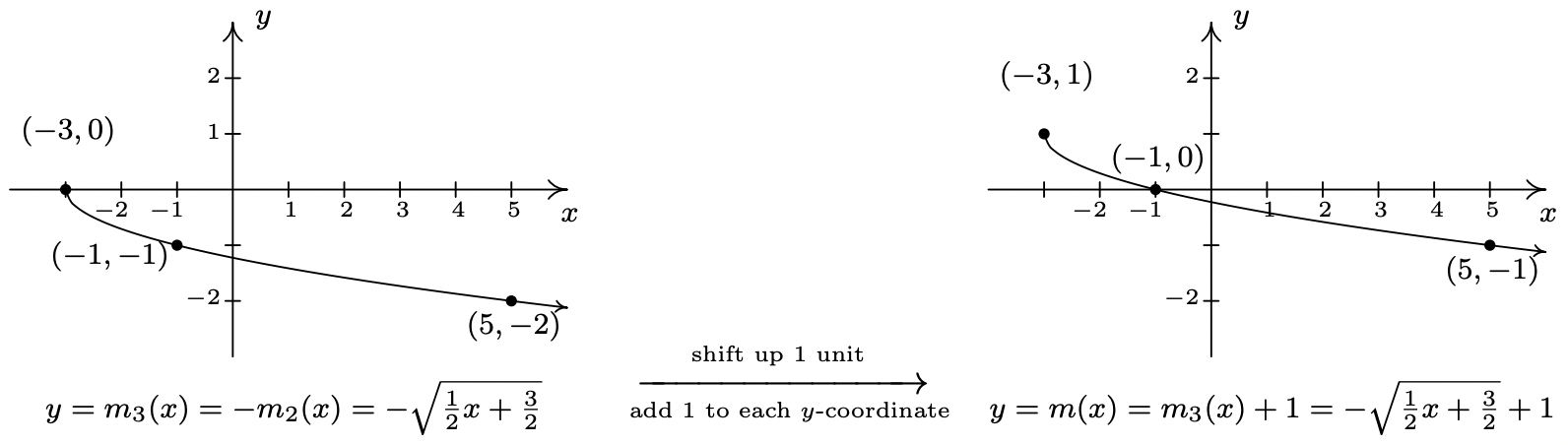
Algunos comentarios sobre el Ejemplo 1.7.3 están en orden. Primero, recordando las propiedades de los radicales del Álgebra Intermedia, sabemos que las funciones\(g\) y\(j\) son las mismas, ya que\(j\) y\(g\) tienen los mismos dominios y\(j(x) = \sqrt{9x} = \sqrt{9} \sqrt{x} = 3 \sqrt{x} = g(x)\). (Invitamos al lector a verificar que todos los puntos que trazamos en la gráfica de se\(g\) encuentran en la gráfica de\(j\) y viceversa). De ahí\(f(x) = \sqrt{x}\), para, un estiramiento vertical por un factor de\(3\) y una contracción horizontal por un factor de\(9\) resultado en la misma transformación. Si bien este tipo de fenómenos no es universal, ocurre con bastante frecuencia con algunas de las familias de funciones estudiadas en Álgebra Universitaria que es digno de mención. En segundo lugar, para graficar la función\(m\), aplicamos una serie de cuatro transformaciones. Si bien hubiera sido más fácil para los autores simplemente informar al lector de qué pasos dar, nos hemos esforzado por explicar por qué el orden en que se aplicaron las transformaciones tenía sentido. Generalizamos el procedimiento en el teorema a continuación.
Supongamos que\(f\) es una función. Si\(A \neq 0\) y\(B \neq 0\), a continuación, para graficar\[g(x) = A f(Bx+H)+K\]
- Restar\(H\) de cada una de las\(x\) -coordenadas de los puntos en la gráfica de\(f\). Esto da como resultado un desplazamiento horizontal hacia la izquierda si\(H > 0\) o derecha si\(H< 0\).
- Divida por las\(x\) coordenadas -de los puntos de la gráfica obtenida en el Paso 1\(B\). Esto da como resultado una escala horizontal, pero también puede incluir una reflexión sobre el\(y\) eje -si\(B < 0\).
- Multiplique por las\(y\) coordenadas -de los puntos de la gráfica obtenida en el Paso 2\(A\). Esto da como resultado una escala vertical, pero también puede incluir una reflexión sobre el\(x\) eje -si\(A < 0\).
- \(K\)Sumar a cada una de las\(y\) -coordenadas de los puntos en la gráfica obtenida en el Paso 3. Esto da como resultado un desplazamiento vertical hacia arriba si\(K > 0\) o hacia abajo si\(K< 0\).
El teorema 1.7 se puede establecer generalizando las técnicas desarrolladas en esta sección. Supongamos que\((a,b)\) está en la gráfica de\(f\). Entonces\(f(a) = b\), y para hacer buen uso de este hecho, nos fijamos\(Bx+H = a\) y resolvemos. Primero restamos el\(H\) (causando el desplazamiento horizontal) y luego dividimos por\(B\). Si\(B\) es un número positivo, esto induce solo un escalado horizontal por un factor de\(\frac{1}{B}\). Si\(B<0\), entonces tenemos un factor de\(-1\) en juego, y dividirlo por él induce una reflexión sobre el\(y\) eje. Así que tenemos\(x = \frac{a-H}{B}\) como entrada a la\(g\) que corresponde la entrada\(x=a\) a\(f\). Ahora evaluamos\(g\left( \frac{a-H}{B}\right) = A f\left(B \cdot \frac{a-H}{B} + H\right) + K = A f(a)+K = A b + K\). Notamos que la salida de\(f\) se multiplica primero por\(A\). Al igual que con la constante\(B\)\(A > 0\), si, esto induce sólo un escalado vertical. Si\(A < 0\), entonces el\(-1\) induce una reflexión a través del\(x\) eje. Por último, sumamos\(K\) al resultado, que es nuestro desplazamiento vertical. Una forma menos precisa, pero más intuitiva de parafrasear el Teorema 1.7 es pensar que la cantidad\(Bx+H\) es el 'interior' de la función\(f\). Lo que está sucediendo en el interior\(f\) afecta a las entradas o\(x\) -coordenadas de los puntos en la gráfica de\(f\). Para encontrar las\(x\) -coordenadas de los puntos correspondientes en\(g\), deshacemos lo que se ha hecho de la misma manera que resolveríamos una ecuación.\(x\) Lo que está sucediendo con la salida puede pensarse como cosas que suceden 'fuera' de la función,\(f\). Las cosas que suceden en el exterior afectan las salidas o\(y\) -coordenadas de los puntos en la gráfica de\(f\). Aquí, seguimos el acuerdo habitual de orden de operaciones: primero multiplicamos por\(A\) luego sumamos\(K\) para encontrar las\(y\) coordenadas correspondientes en la gráfica de\(g\).
A continuación se muestra la gráfica completa de\(y = f(x)\). Úselo para graficar\(g(x) = \frac{4-3 f(1-2x)}{2}\).
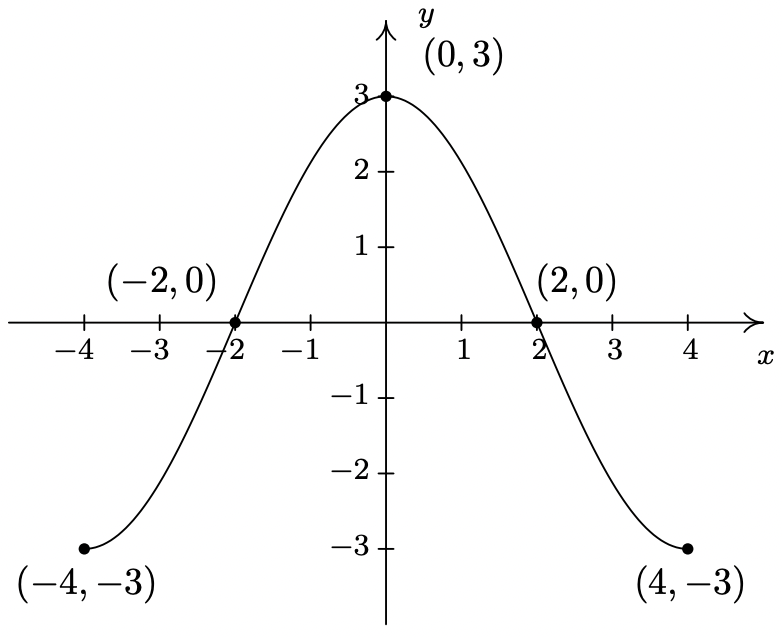
Solución
Utilizamos el Teorema 1.7 para rastrear los cinco 'puntos claves'\((-4,-3)\)\((-2,0)\),\((0,3)\),\((2,0)\) e\((4,-3)\) indicados en la gráfica de\(f\) a sus nuevas ubicaciones. Primero reescribimos\(g(x)\) en la forma presentada en Teorema 1.7,\(g(x) = -\frac{3}{2}f(-2x+1) +2\). Establecemos\(-2x+1\) iguales a las\(x\) coordenadas -de los puntos clave y resolvemos. Por ejemplo, resolviendo\(-2x+1 = -4\), primero restamos\(1\) para obtener\(-2x = -5\) luego dividimos por\(-2\) para obtener\(x = \frac{5}{2}\). Restar el\(1\) es un desplazamiento horizontal hacia la\(1\) unidad izquierda. Dividir por\(-2\) puede pensarse como un proceso de dos pasos: dividir por el\(2\) cual comprime la gráfica horizontalmente por un factor de\(2\) seguido de dividir (multiplicar) por\(-1\) lo que provoca una reflexión a través del\(y\) eje. Resumimos los resultados en la tabla de la página siguiente.
\ (\\ begin {array} {|r||r|r|r|}
\ hline (a, f (a)) & a y -2 x+1 = a & x
\\ hline (-4, -3) & -4 y -2 x+1 = -4 & x=\ frac {5} {2}
\\ hline (-2,0) & -2 x+1=-2 & x=\ frac {3} {2}\
\ hline (0,3) & 0 & -2 x+1 = 0 & x=\ frac {1} {2}\\
\ hline (2,0) & 2 y -2 x+1 = 2 & x=-\ frac {1} {2}\
\ hline (4, -3) & 4 y -2 x+1 = 4 & x=-\ frac {3} {2}\
\ hline
\ end {array}\\)
A continuación, tomamos cada uno de los\(x\) valores y los sustituimos\(g(x) = -\frac{3}{2}f(-2x+1) +2\) para obtener los\(y\) valores -correspondientes. Sustituyendo\(x=\frac{5}{2}\), y usando el hecho de que\(f(-4)=-3\), obtenemos
\(\ g\left(\frac{5}{2}\right)=-\frac{3}{2} f\left(-2\left(\frac{5}{2}\right)+1\right)+2=-\frac{3}{2} f(-4)+2=-\frac{3}{2}(-3)+2=\frac{9}{2}+2=\frac{13}{2}\)
Vemos que la salida de primero\(f\) se multiplica por\(-\frac{3}{2}\). Pensando en esto como un proceso de dos pasos, multiplicando para\(\frac{3}{2}\) entonces por\(-1\), tenemos un estiramiento vertical por un factor de\(\frac{3}{2}\) seguido de una reflexión a través del\(x\) eje. Agregando\(2\) resultados en un desplazamiento vertical hacia arriba de\(2\) unidades. Continuando de esta manera, obtenemos la siguiente tabla.
\ (\\ begin {array} {|r||r|r|}
\ hline x & g (x) & (x, g (x))\
\ hline\ frac {5} {2} &\ frac {13} {2} &\ izquierda (\ frac {5} {2},\ frac {13} {2}\ derecha)\
\ hline\ frac {3} {2} & 2 &\ izquierda (\ frac {3} {2}, 2\ derecha)\
\ hline\ frac {1} {2} & -\ frac {5} {2} &\ izquierda (\ frac {1} {2}, -\ frac {5} {2}\ derecha)\
\ hline-\ frac {1} {2} & 2 &\ izquierda (-\ frac {1} {2}, 2\ derecha)\
\ hline-\ frac {3} {2} &\ frac {13} {2} &\ izquierda (-\ frac {3} {2},\ frac {13} {2}\ derecha)\\
\ hline
\ end {array}\)
Para graficar\(g\), trazamos cada uno de los puntos de la tabla anterior y los conectamos en el mismo orden y manera que los puntos a los que corresponden. Trazado\(f\) y\(g\) lado a lado da
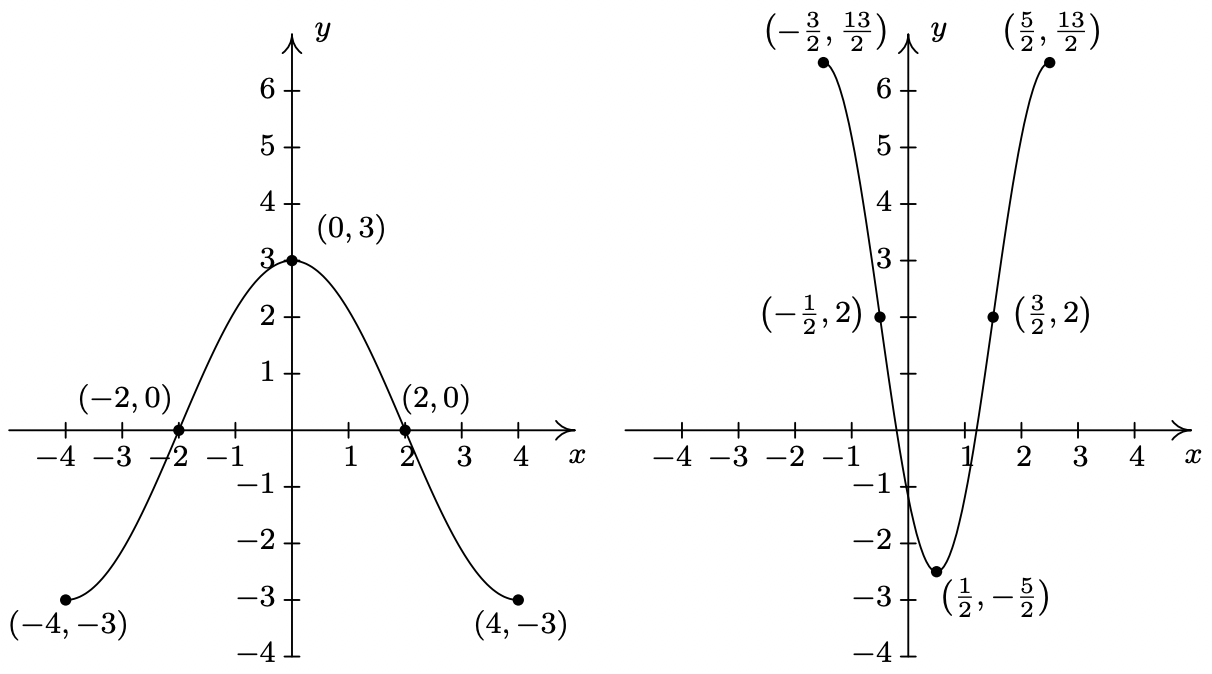
Se recomienda encarecidamente al lector 11 graficar la serie de funciones que muestra la transformación gradual de la gráfica de\(f\) en la gráfica de\(g\). Hemos esbozado la secuencia de transformaciones en la exposición anterior; lo único que queda es trazar las cinco etapas intermedias.
Nuestro último ejemplo da vuelta a las tornas y pide la fórmula de una función dada una secuencia deseada de transformaciones. Si nada más, es una buena revisión de la notación de funciones.
Vamos\(f(x) = x^2\). Encontrar y simplificar la fórmula de la función\(g(x)\) cuya gráfica es el resultado de\(f\) sufrir la siguiente secuencia de transformaciones. Comprueba tu respuesta usando una calculadora gráfica.
- \(2\)Unidades de cambio vertical
- Reflexión a través del\(x\) eje
- \(1\)Unidad de cambio horizontal a la derecha
- Estiramiento horizontal por un factor de\(2\)
Solución
Construimos hasta una fórmula para\(g(x)\) usar funciones intermedias como hemos visto en ejemplos anteriores. Dejamos\(g_{1}\) encargarnos de nuestro primer paso. El teorema 1.2 nos dice\(g_{1}(x) = f(x) + 2 = x^2+2\). A continuación, reflejamos la gráfica de\(g_{1}\) alrededor del\(x\) eje -usando el Teorema 1.4:\(g_{2}(x) = -g_{1}(x) = -\left(x^2+2\right) = -x^2-2\). Cambiamos la gráfica a la\(1\) unidad derecha, según el Teorema 1.3, fijando\(g_{3}(x) = g_{2}(x-1) = -(x-1)^2-2 = -x^2+2x-3\). Finalmente, inducimos un estiramiento horizontal por un factor de\(2\) usar el Teorema 1.6 para obtener\(g(x) = g_{3}\left(\frac{1}{2} x\right) = -\left(\frac{1}{2} x\right)^2+2\left(\frac{1}{2} x\right)-3\) qué rendimientos\(g(x) = -\frac{1}{4} x^2 + x -3\). Utilizamos la calculadora para graficar las etapas a continuación para confirmar nuestro resultado.
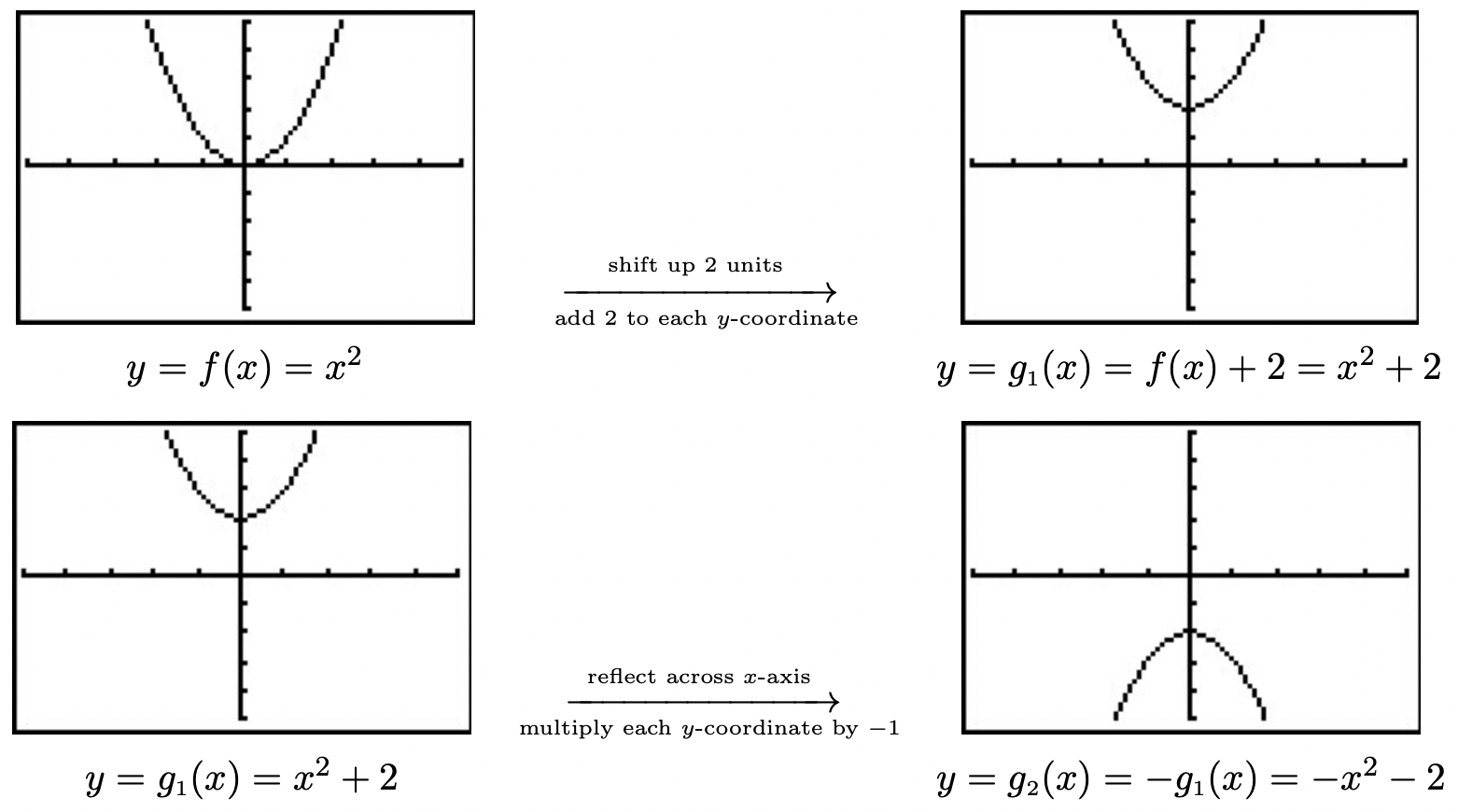
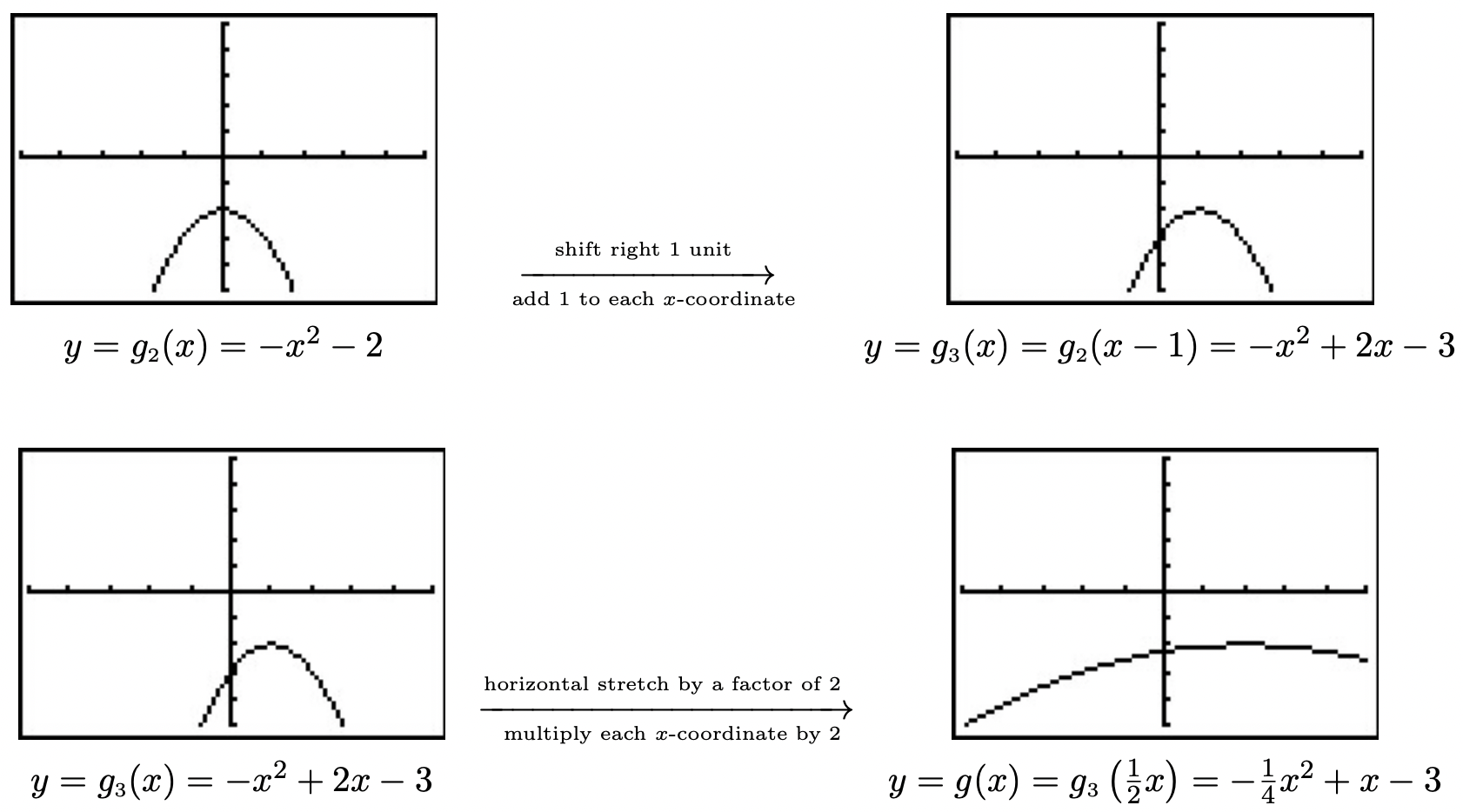
Hemos mantenido la ventana de visualización igual en todas las gráficas anteriores. Esto tuvo la consecuencia indeseable de hacer que la última gráfica pareciera 'incompleta' en la que no podemos ver la forma original de\(f(x) = x^{2}\). Alterar la ventana de visualización da como resultado una gráfica más completa de la función transformada como se ve a continuación.
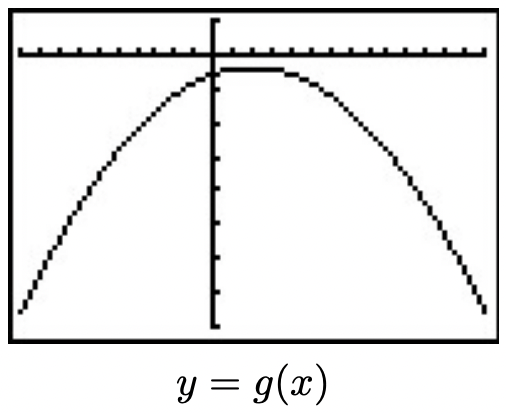
Este ejemplo acerca a nuestro primer capítulo a su fin. En los capítulos que tenemos por delante, estar atentos a los conceptos que aquí se desarrollan para resurgir a medida que estudiamos diferentes familias de funciones.
1.7.1 Ejercicios
Supongamos que\((2,-3)\) está en la gráfica de\(y = f(x)\). En los Ejercicios 1 - 8, utilice el Teorema 1.7 para encontrar un punto en la gráfica de la función transformada dada.
- \(y = f(x)+3\)
- \(y = f(x+3)\)
- \(y = f(x)-1\)
- \(y = f(x-1)\)
- \(y = 3f(x)\)
- \(y = f(3x)\)
- \(y = -f(x)\)
- \(y = f(-x)\)
- \(y = f(x-3)+1\)
- \(y = 2f(x+1)\)
- \(y = 10 - f(x)\)
- \(y = 3f(2x) - 1\)
- \(y = \frac{1}{2} f(4-x)\)
- \(y = 5f(2x+1) + 3\)
- \(y = 2f(1-x) -1\)
- \(y =f\left(\dfrac{7-2x}{4}\right)\)
- \(y = \dfrac{f(3x) - 1}{2}\)
- \(y = \dfrac{4-f(3x-1)}{7}\)
La gráfica completa de\(y = f(x)\) se da a continuación. En los Ejercicios 19 - 27, utilícelo y Teorema 1.7 para graficar la función transformada dada.
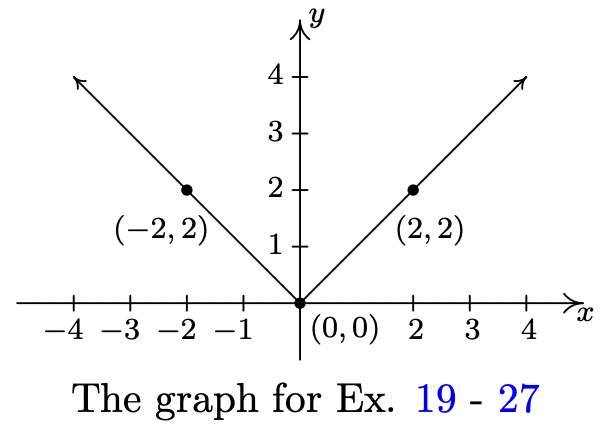
- \(y = f(x) + 1\)
- \(y = f(x) - 2\)
- \(y = f(x+1)\)
- \(y = f(x - 2)\)
- \(y = 2f(x)\)
- \(y = f(2x)\)
- \(y = 2 - f(x)\)
- \(y = f(2-x)\)
- \(y = 2-f(2-x)\)
- Algunas de las respuestas a los Ejercicios 19 - 27 anteriores deberían ser las mismas. ¿Cuáles coinciden? ¿Qué propiedades de la gráfica de\(y=f(x)\) contribuyen a la duplicación?
La gráfica completa de\(y = f(x)\) se da a continuación. En los Ejercicios 29 - 37, utilícelo y Teorema 1.7 para graficar la función transformada dada.
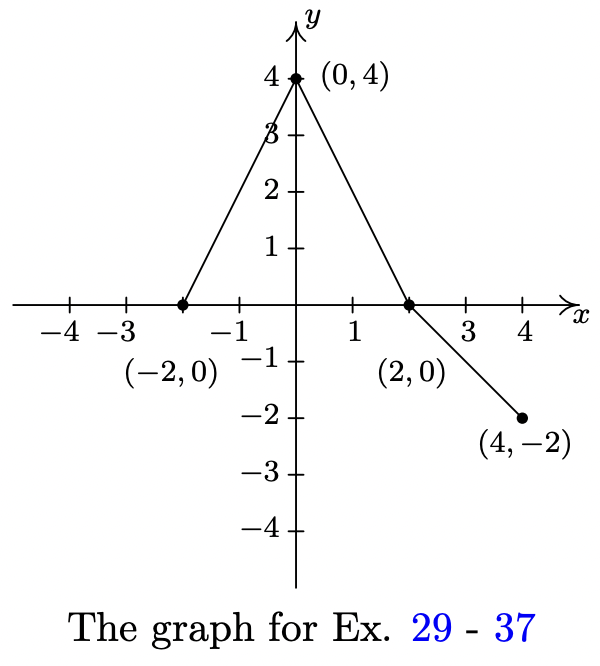
- \(y = f(x) - 1\)
- \(y = f(x + 1)\)
- \(y = \frac{1}{2} f(x)\)
- \(y = f(2x)\)
- \(y = - f(x)\)
- \(y = f(-x)\)
- \(y = f(x+1) - 1\)
- \(y = 1 - f(x)\)
- \(y = \frac{1}{2}f(x+1)-1\)
La gráfica completa de\(y = f(x)\) se da a continuación. En los Ejercicios 38 - 49, utilícelo y Teorema 1.7 para graficar la función transformada dada.
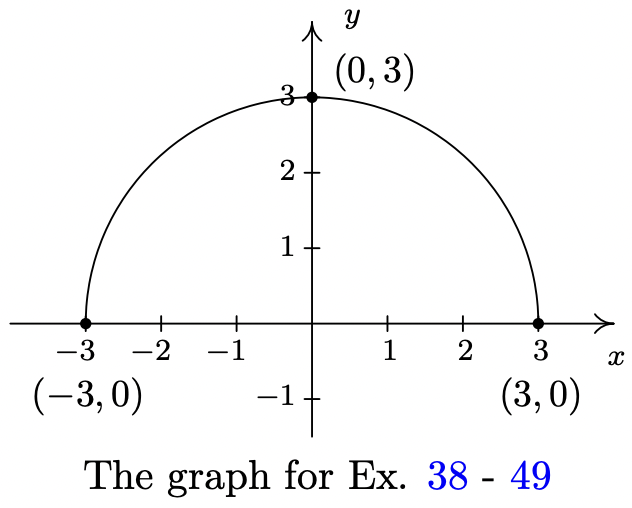
- \(g(x) = f(x) + 3\)
- \(h(x) = f(x) - \frac{1}{2}\)
- \(j(x) = f\left(x - \frac{2}{3}\right)\)
- \(a(x) = f(x + 4)\)
- \(b(x) = f(x + 1) - 1\)
- \(c(x) = \frac{3}{5}f(x)\)
- \(d(x) = -2f(x)\)
- \(k(x) = f\left(\frac{2}{3}x\right)\)
- \(m(x) = -\frac{1}{4}f(3x)\)
- \(n(x) = 4f(x - 3) - 6\)
- \(p(x) = 4 + f(1 - 2x)\)
- \(q(x) = -\frac{1}{2}f\left(\frac{x + 4}{2}\right) - 3\)
La gráfica completa de\(y = S(x)\) se da a continuación.
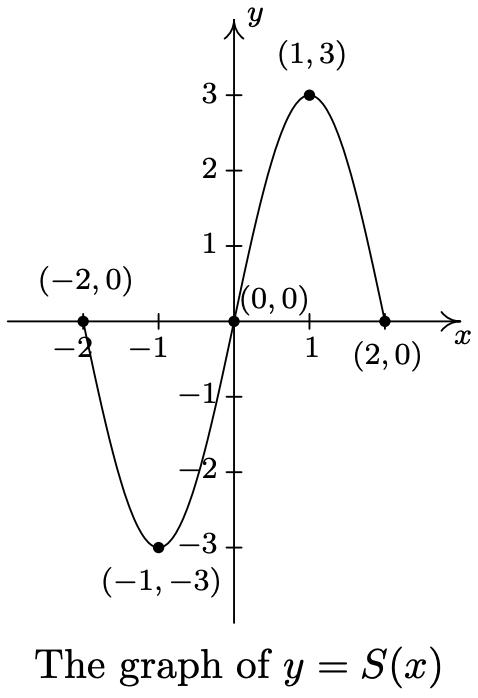
El propósito de los Ejercicios 50 - 53 es graficar\(y = \frac{1}{2}S(-x+1) + 1\) graficando cada transformación, paso a paso.
- \(\ y=S_{1}(x)=S(x+1)\)
- \(\ y=S_{2}(x)=S_{1}(-x)=S(-x+1)\)
- \(\ y=S_{3}(x)=\frac{1}{2} S_{2}(x)=\frac{1}{2} S(-x+1)\)
- \(\ y=S_{4}(x)=S_{3}(x)+1=\frac{1}{2} S(-x+1)+1\)
Vamos\(f(x) = \sqrt{x}\). Encuentra una fórmula para una función\(g\) cuya gráfica se obtiene a\(f\) partir de la secuencia dada de transformaciones.
- (1) cambiar a la derecha 2 unidades; (2) cambiar hacia abajo 3 unidades
- (1) cambiar hacia abajo 3 unidades; (2) cambiar a la derecha 2 unidades
- (1) reflejar a través del\(x\) eje; (2) cambiar hacia arriba 1 unidad
- (1) cambiar hacia arriba 1 unidad; (2) reflejar a través del\(x\) eje
- (1) cambiar a la izquierda 1 unidad; (2) reflejar a través del\(y\) eje; (3) cambiar hacia arriba 2 unidades
- (1) reflejar a través del\(y\) eje; (2) cambiar a la izquierda 1 unidad; (3) cambiar hacia arriba 2 unidades
- (1) desplazamiento a la izquierda 3 unidades; (2) estiramiento vertical por un factor de 2; (3) desplazamiento hacia abajo 4 unidades
- (1) desplazamiento a la izquierda 3 unidades; (2) desplazamiento hacia abajo 4 unidades; (3) estiramiento vertical por un factor de 2
- (1) cambiar a la derecha 3 unidades; (2) contracción horizontal por un factor de 2; (3) cambio hacia arriba 1 unidad
- (1) contracción horizontal por un factor de 2; (2) cambiar a la derecha 3 unidades; (3) cambiar hacia arriba 1 unidad
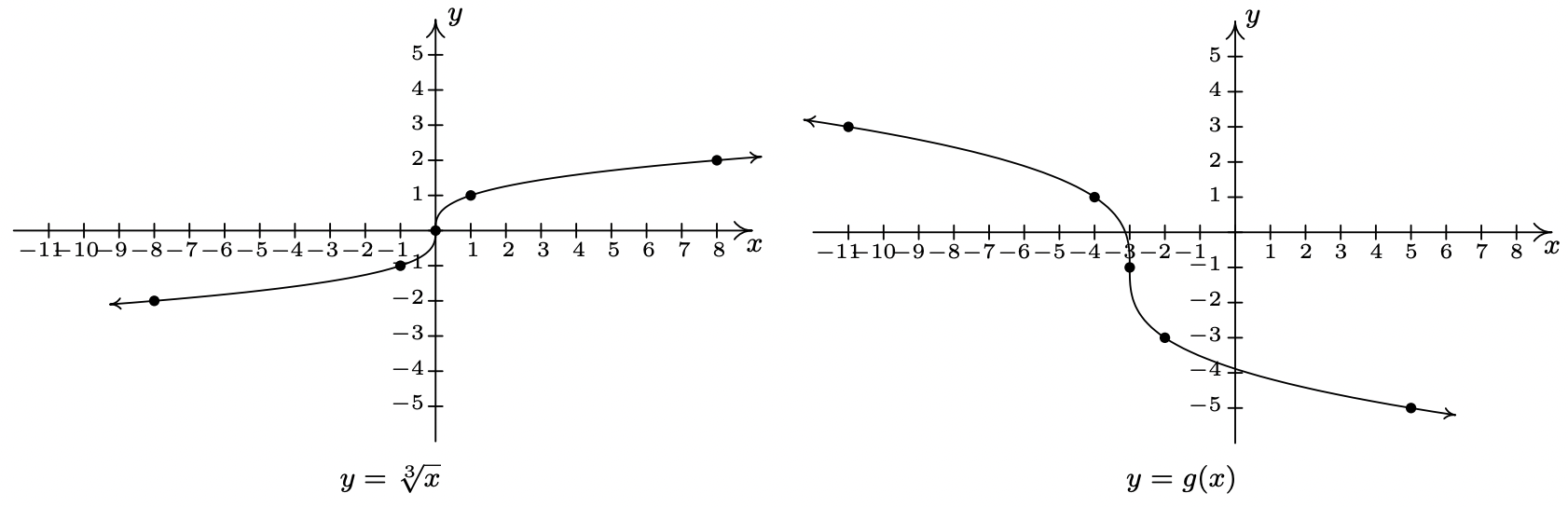
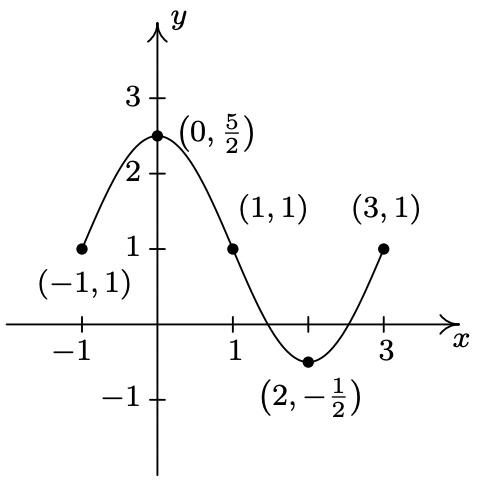
- La gráfica de\(y = f(x) = \sqrt[3]{x}\) se da a continuación a la izquierda y la gráfica de\(y = g(x)\) se da a la derecha. Encuentra una fórmula para\(g\) basada en transformaciones de la gráfica de\(f\). Comprueba tu respuesta confirmando que los puntos mostrados en la gráfica de\(g\) satisfacen la ecuación\(y = g(x)\).
- Para muchas funciones comunes, las propiedades de Álgebra hacen que una escala horizontal sea igual que una escala vertical por (posiblemente) un factor diferente. Por ejemplo, ya lo afirmamos antes\(\sqrt{9x} = 3\sqrt{x}\). Con la ayuda de tus compañeros de clase, encuentra el escalado vertical equivalente producido por los escalados horizontales\(y = (2x)^{3}, \, y = |5x|, \, y = \sqrt[3]{27x} \,\) y\(\, y = \left(\frac{1}{2} x\right)^{2}\). ¿Qué pasa\(y = (-2x)^{3}, \, y = |-5x|, \, y = \sqrt[3]{-27x}\,\) y\(\, y = \left(-\frac{1}{2} x\right)^{2}\)?
- Ya mencionamos anteriormente en el apartado que, en general, importa el orden en que se aplican las transformaciones, sin embargo, en nuestro primer ejemplo con dos transformaciones el orden no importaba. (Podrías realizar el turno a la izquierda seguido del cambio hacia abajo o podrías cambiar hacia abajo y luego a la izquierda para lograr el mismo resultado). Con la ayuda de tus compañeros, determina las situaciones en las que el orden sí importa y aquellas en las que no.
- ¿Qué sucede si reflejas una función par a través del\(y\) eje -axis?
- ¿Qué sucede si refleja una función impar a través del\(y\) eje -axis?
- ¿Qué sucede si reflejas una función par a través del\(x\) eje -axis?
- ¿Qué sucede si refleja una función impar a través del\(x\) eje -axis?
- ¿Cómo describiría la simetría sobre el origen en términos de reflexiones?
- Como vimos en el Ejemplo 1.7.5, la ventana de visualización en la calculadora gráfica afecta a cómo vemos las transformaciones hechas a una gráfica. Usando dos calculadoras diferentes, encuentra ventanas de visualización para que\(f(x) = x^{2}\) en una calculadora se vea como\(g(x) = 3x^{2}\) en la otra.
1.7.2 Respuestas
- \((2,0)\)
- \((-1,-3)\)
- \((2,-4)\)
- \((3,-3)\)
- \((2,-9)\)
- \(\left(\frac{2}{3}, -3\right)\)
- \((2,3)\)
- \((-2,-3)\)
- \((5,-2)\)
- \((1,-6)\)
- \((2,13)\)
- \(y = (1,-10)\)
- \(\left(2, -\frac{3}{2}\right)\)
- \(\left(\frac{1}{2}, -12 \right)\)
- \((-1,-7)\)
- \(\left(-\frac{1}{2}, -3\right)\)
- \(\left(\frac{2}{3}, -2 \right)\)
- \((1,1)\)
- \(y = f(x) + 1\)
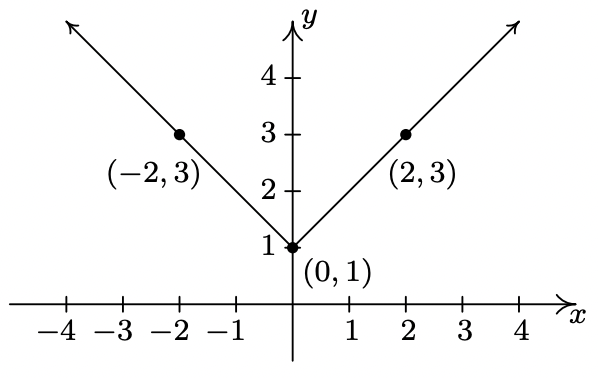
- \(y = f(x) - 2\)
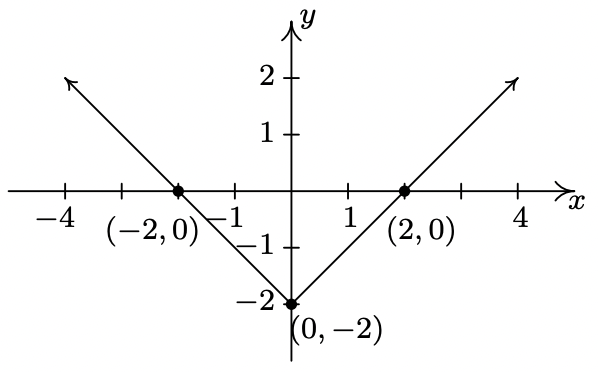
- \(y = f(x+1)\)
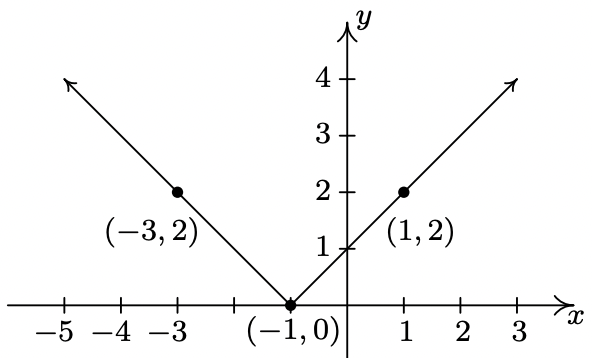
- \(y = f(x - 2)\)
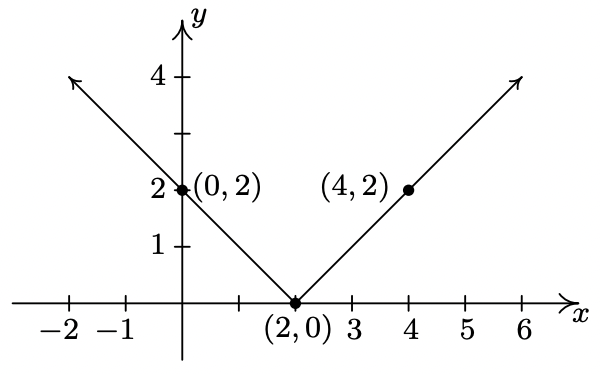
- \(y = 2f(x)\)
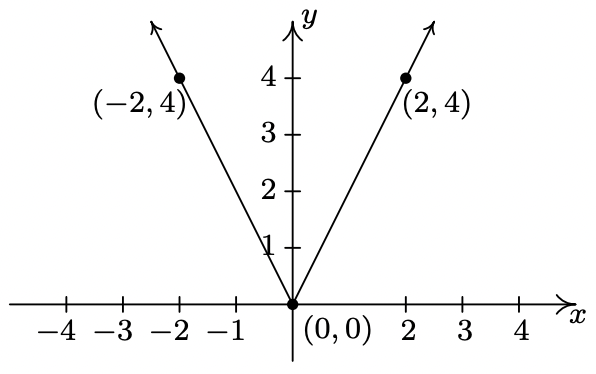
- \(y = f(2x)\)
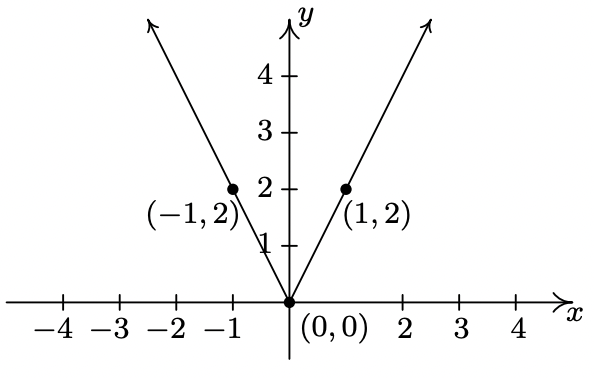
- \(y = 2 - f(x)\)
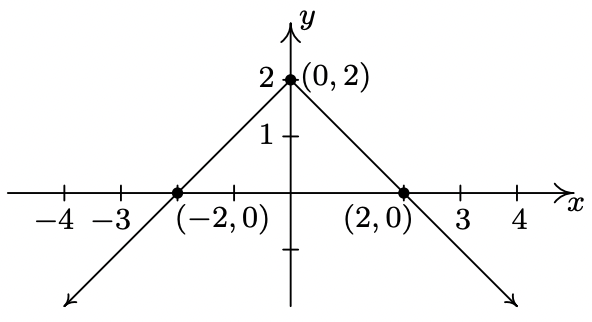
- \(y = f(2-x)\)
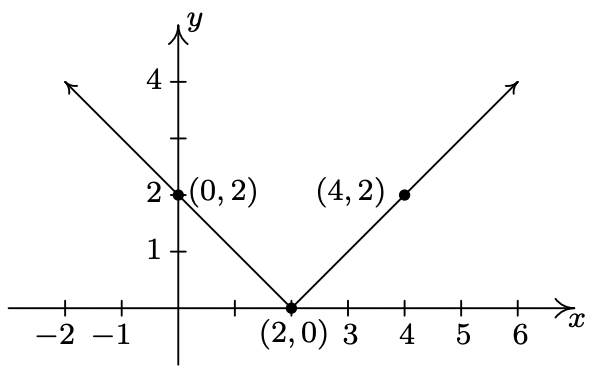
- \(y = 2-f(2-x)\)
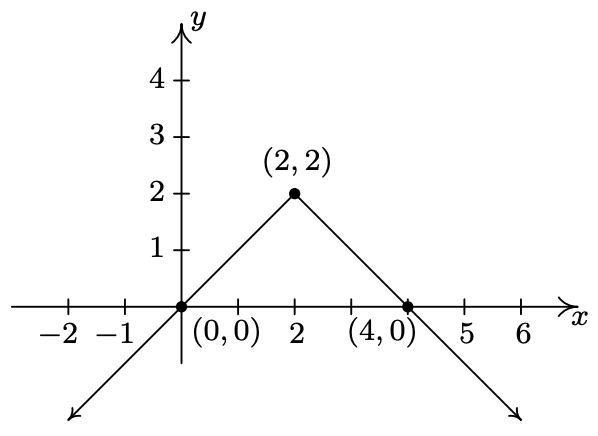
- \(y = f(x) - 1\)
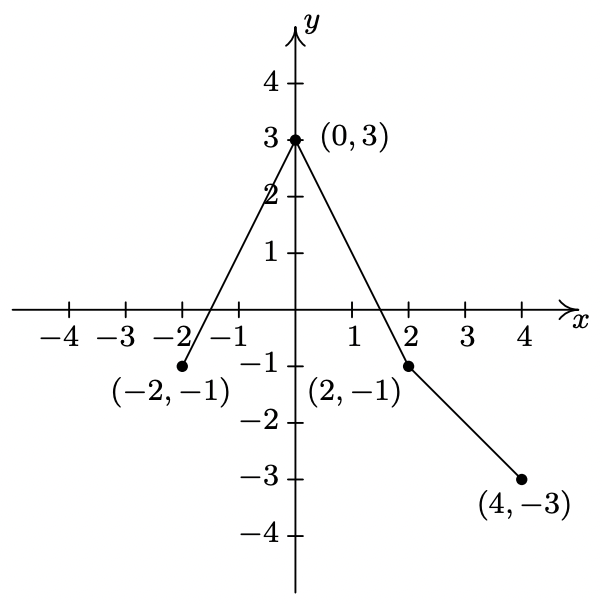
- \(y = f(x + 1)\)
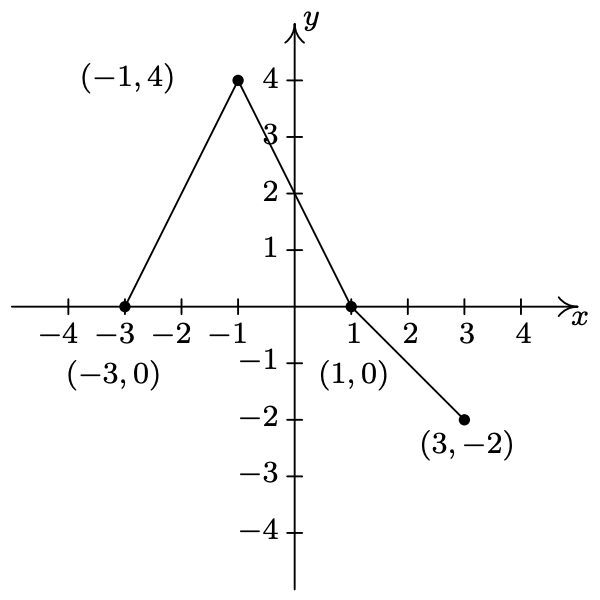
- \(y = \frac{1}{2} f(x)\)
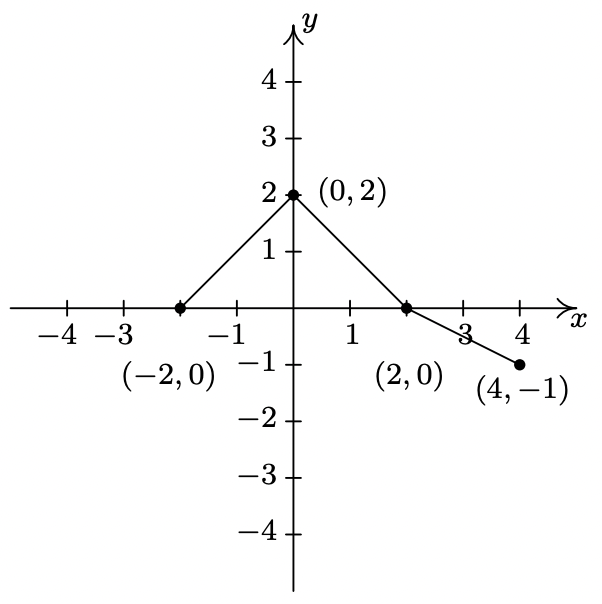
- \(y = f(2x)\)
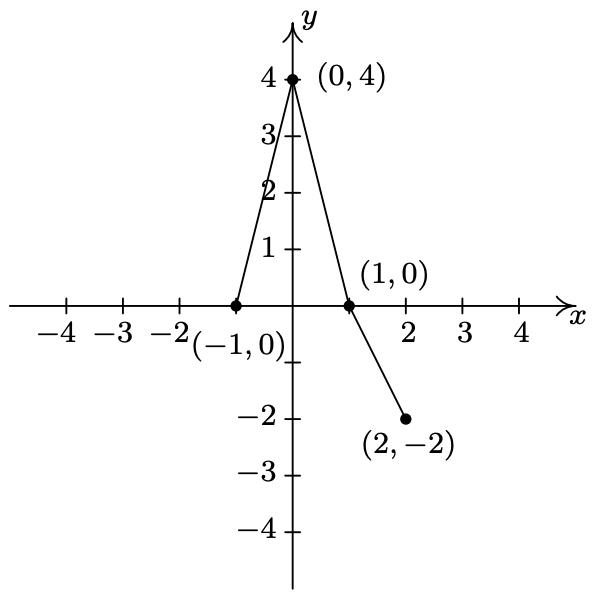
- \(y = - f(x)\)
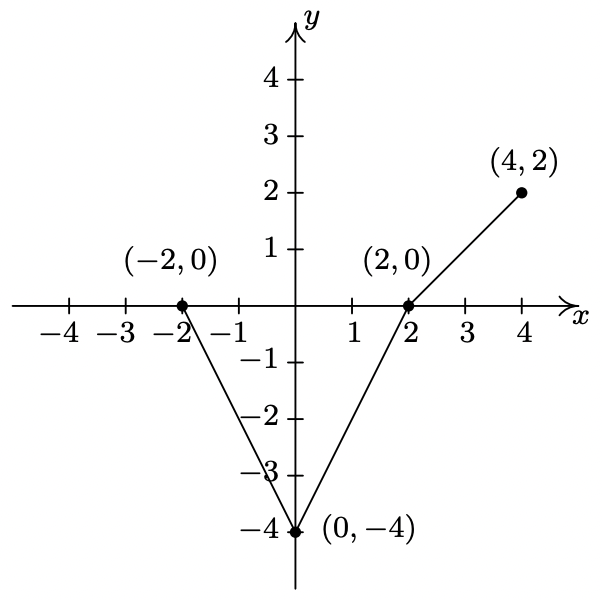
- \(y = f(-x)\)
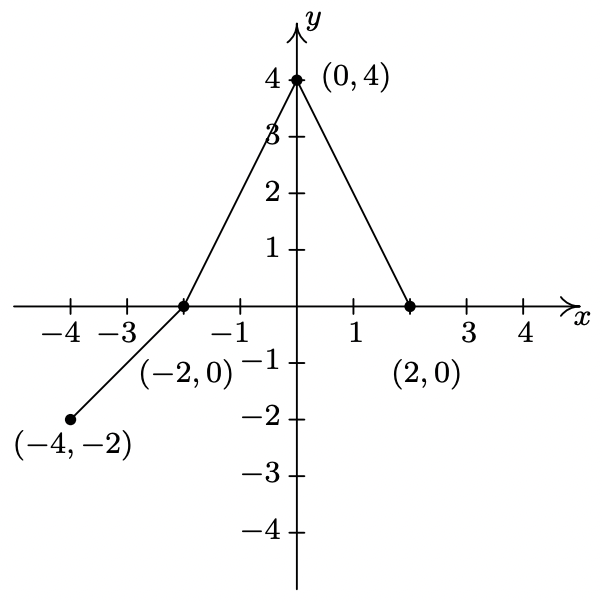
- \(y = f(x+1) - 1\)
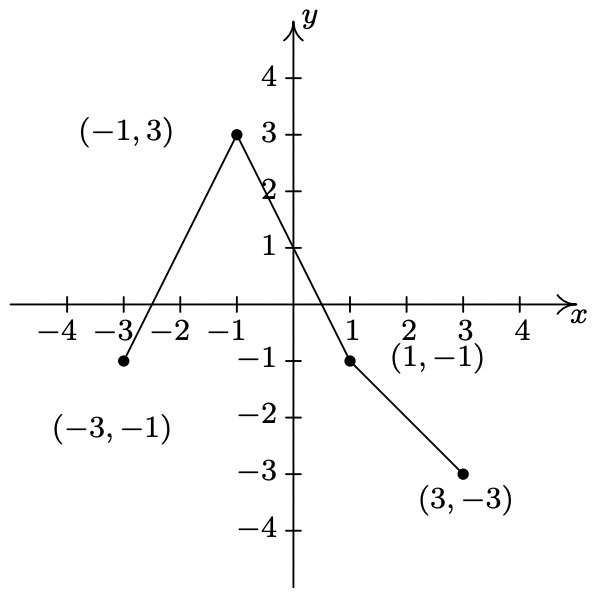
- \(y = 1 - f(x)\)
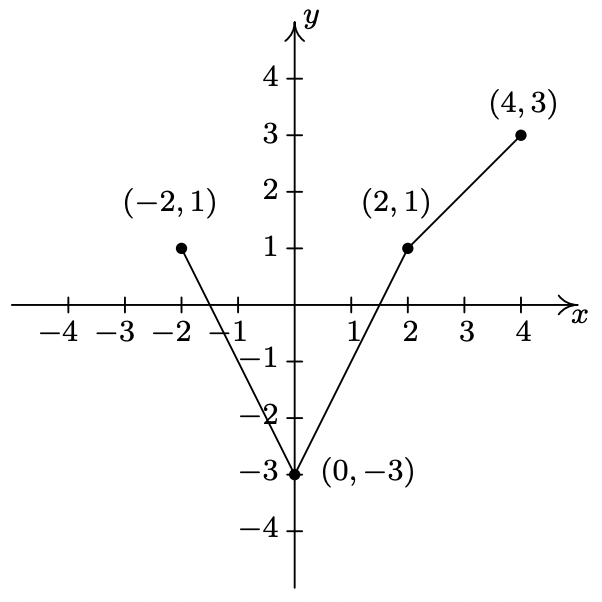
- \(y = \frac{1}{2}f(x+1)-1\)
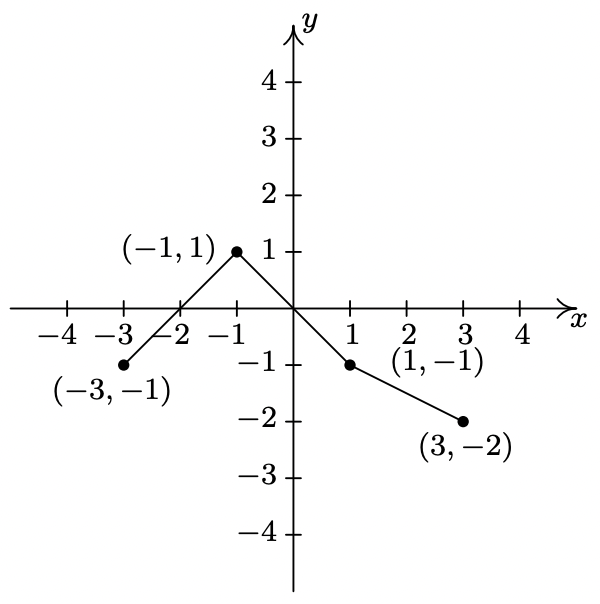
- \(g(x) = f(x) + 3\)
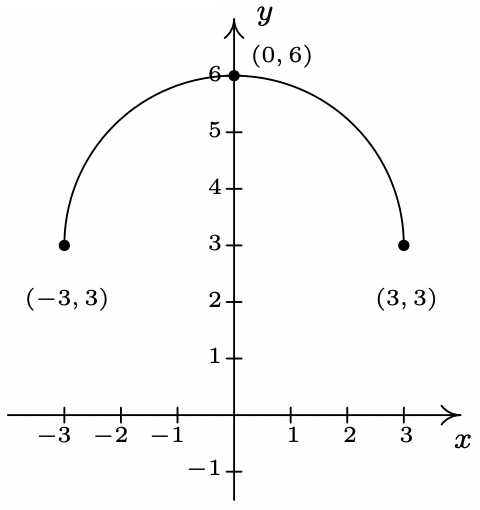
- \(h(x) = f(x) - \frac{1}{2}\)
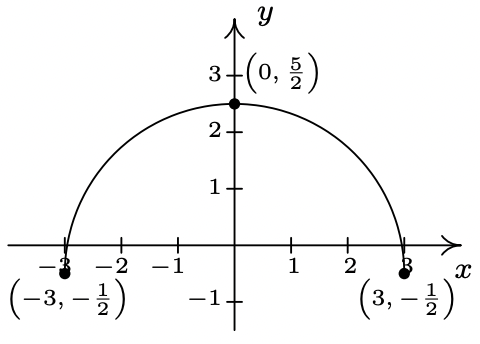
- \(j(x) = f\left(x - \frac{2}{3}\right)\)
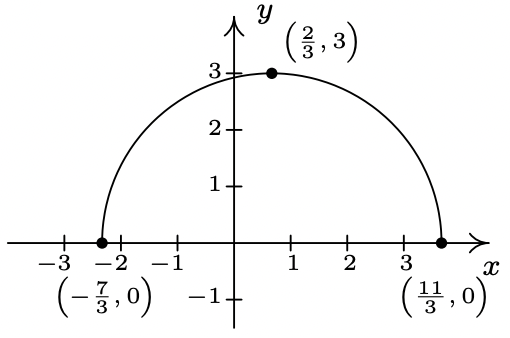
- \(a(x) = f(x + 4)\)
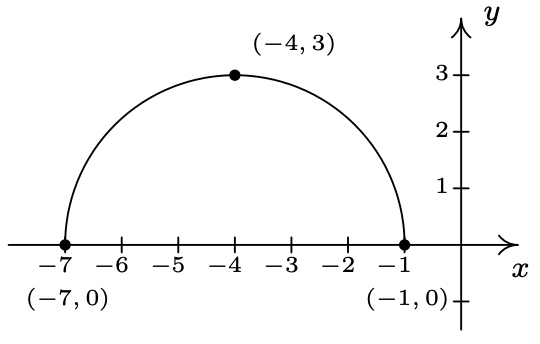
- \(b(x) = f(x + 1) - 1\)
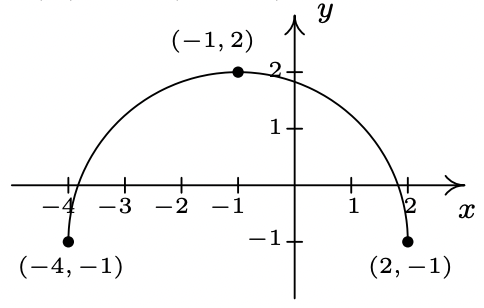
- \(c(x) = \frac{3}{5}f(x)\)
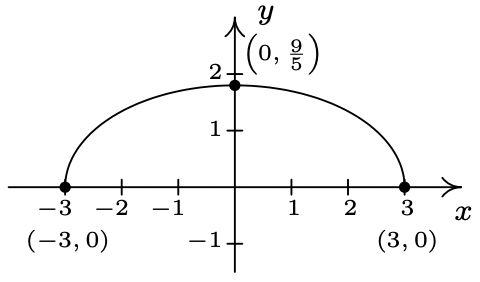
- \(d(x) = -2f(x)\)
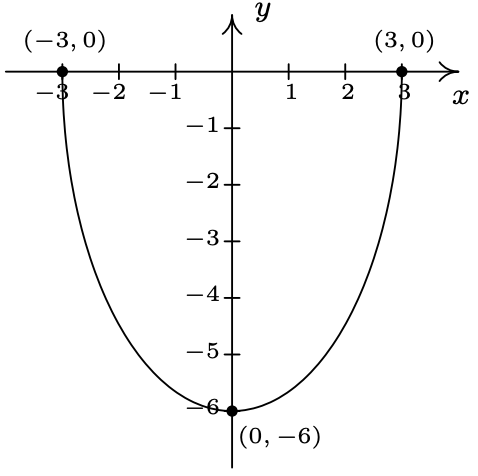
- \(k(x) = f\left(\frac{2}{3}x\right)\)
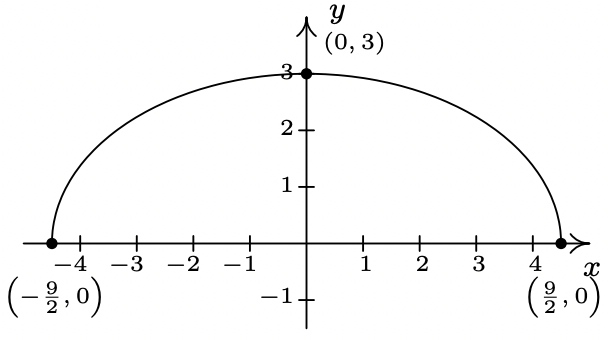
- \(m(x) = -\frac{1}{4}f(3x)\)
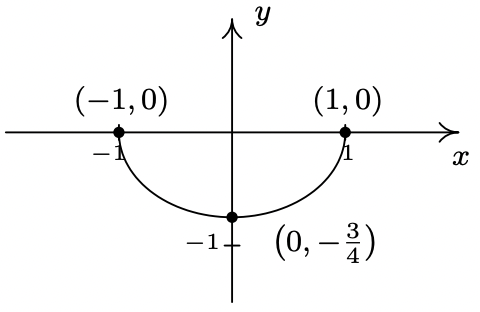
- \(n(x) = 4f(x - 3) - 6\)
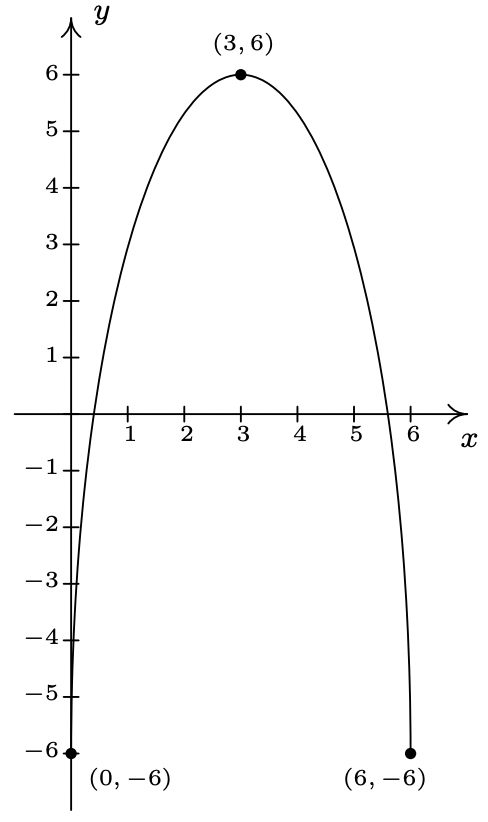
- \(p(x) = 4 + f(1 - 2x) = f(-2x + 1) + 4\)
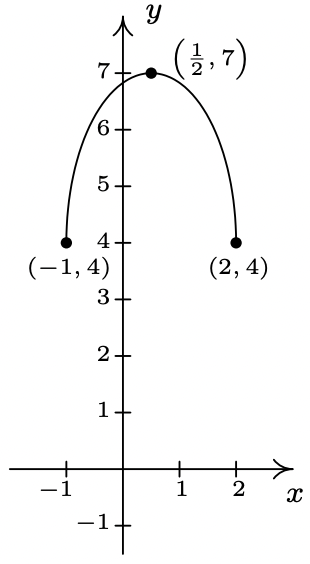
- \(q(x) = -\frac{1}{2}f\left(\frac{x + 4}{2}\right) - 3 = -\frac{1}{2}f\left( \frac{1}{2}x + 2 \right) - 3\)
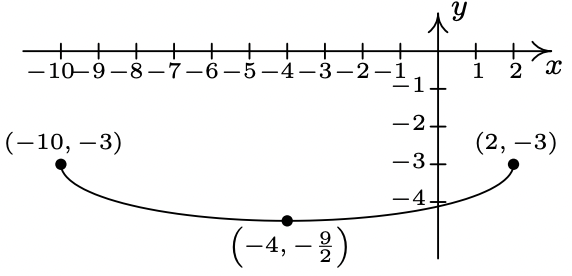
- \(\ y=S_{1}(x)=S(x+1)\)
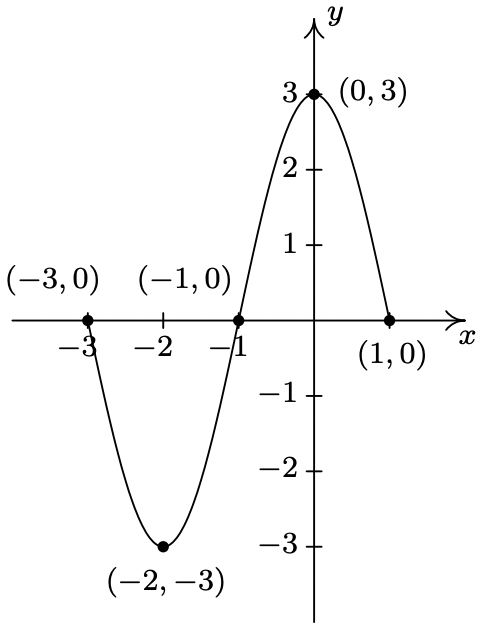
- \(\ y=S_{2}(x)=S_{1}(-x)=S(-x+1)\)
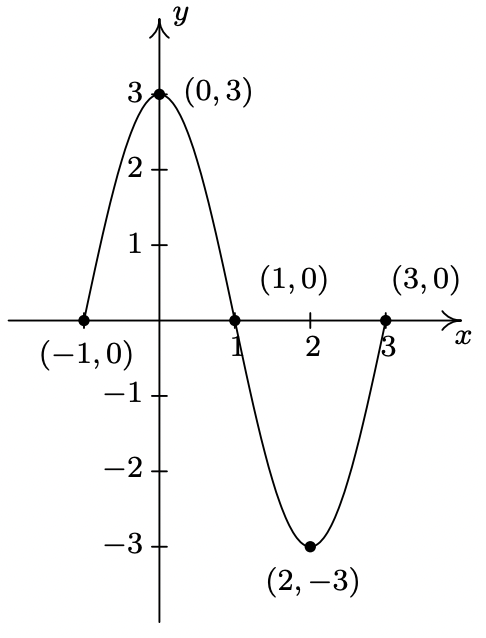
- \(\ y=S_{3}(x)=\frac{1}{2} S_{2}(x)=\frac{1}{2} S(-x+1)\)
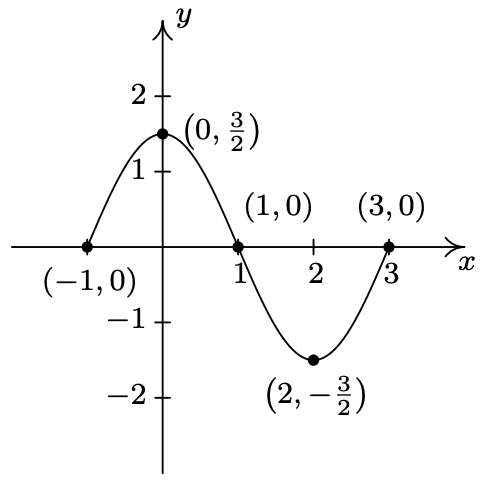
- \(\ y=S_{4}(x)=S_{3}(x)+1=\frac{1}{2} S(-x+1)+1\)
- \(g(x) = \sqrt{x-2} - 3\)
- \(g(x) = \sqrt{x-2} - 3\)
- \(g(x) = -\sqrt{x} + 1\)
- \(g(x) = -(\sqrt{x} + 1) = -\sqrt{x} - 1\)
- \(g(x) = \sqrt{-x+1} + 2\)
- \(g(x) = \sqrt{-(x+1)} + 2 = \sqrt{-x-1} + 2\)
- \(g(x) = 2\sqrt{x+3} - 4\)
- \(g(x) = 2\left(\sqrt{x+3} - 4\right) = 2\sqrt{x+3} - 8\)
- \(g(x) = \sqrt{2x-3} + 1\)
- \(g(x) = \sqrt{2(x-3)} + 1 = \sqrt{2x-6}+1\)
- \(g(x) = -2\sqrt[3]{x + 3} - 1\)o\(g(x) = 2\sqrt[3]{-x - 3} - 1\)
Referencia
1 Hemos pasado mucho tiempo en este texto mostrándote eso\(\ f(x + 2)\) y\(\ f(x) + 2\) somos, en general, animales algebraicos salvajemente diferentes. Veremos momentáneamente que su geometría también es dramáticamente diferente.
2 Veremos en el siguiente ejemplo que el orden es generalmente importante al aplicar más de una transformación a una gráfica.
3 De igual manera podríamos haber elegido la convención 'salidas primero'.
4 Las expresiones\(\ −f(x)\) y\(\ f(−x)\) deben parecer familiares - son las cantidades que usamos en la Sección 1.6 para probar si una función era par, impar o ninguna. Se invita al lector interesado a explorar el papel de las reflexiones y la simetría de las funciones. ¿Qué sucede si refleja una función par a través del eje y? ¿Qué sucede si refleja una función impar a través del eje y? ¿Qué pasa con el eje x?
5 O dividir - equivale a lo mismo.
6 Si hubiéramos hecho la reflexión primero, entonces\(\ j_{1}(x)=f(-x)\). Seguir esto por un turno a la izquierda nos daría\(\ f(x)=j_{1}(x+3)=f(-(x+3))=f(-x-3)=\sqrt{-x-3}\) que no es lo que queremos. No obstante, si primero hiciéramos la reflexión y la siguiéramos de un turno a la derecha 3 unidades, habríamos llegado a la función\(\ j(x)\). Dejamos al lector verificar los detalles.
7 También se denomina 'estiramiento vertical', 'expansión vertical' o 'dilatación vertical' por un factor de 2.
8 También se llama 'contracción vertical', 'compresión vertical' o 'contracción vertical' por un factor de 2.
9 También se llama 'contracción horizontal', 'compresión horizontal' o 'contracción horizontal' por un factor de 2.
10 También se llama 'estiramiento horizontal', 'expansión horizontal' o 'dilatación horizontal' por un factor de 2.
11 Realmente deberías hacer esto una vez en tu vida.


