Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

7.2: Círculos

Última actualización

30 oct 2022
Guardar como PDF
- 7.1: Introducción a las Cónicas
- 7.3: Parábolas

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Recordemos de Geometría que un círculo se puede determinar fijando un punto (llamado centro) y un número positivo (llamado radio) de la siguiente manera.

Definición 7.1

Un círculo con centro $(h,k)$ y radio $r>0$ es el conjunto de todos $(x, y)$ los puntos del plano cuya distancia a $(h,k)$ es $r$ .

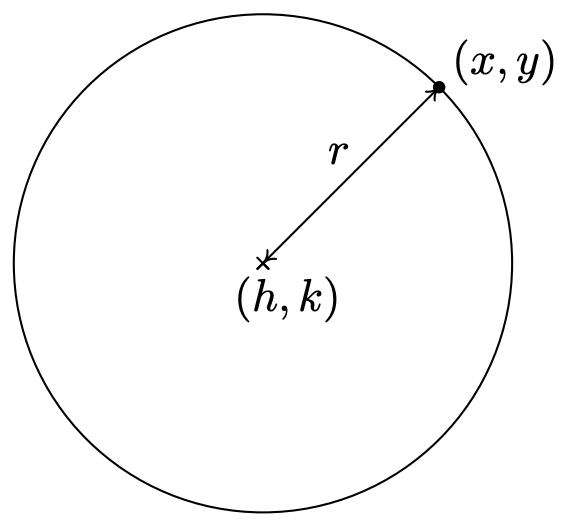
$Screen Shot 2022-04-21 en 4.38.42 PM.png$

De la imagen, vemos que un punto $(x,y)$ está en el círculo si y sólo si su distancia a $(h,k)$ es $r$ . Expresamos esta relación algebraicamente usando la Fórmula de Distancia, Ecuación 1.1, como

$r = \sqrt{(x - h)^2 + (y-k)^2}\nonumber$ Al cuadrar ambos lados de esta ecuación, obtenemos una ecuación equivalente (since

$r > 0$ ) que nos da la ecuación estándar de un círculo.

Ecuación 7.1. La ecuación estándar de un círculo

La ecuación estándar de un círculo: La ecuación de un círculo con centro $(h,k)$ y radio $r >0$ es $(x-h)^2 + (y-k)^2 = r^2.$

Ejemplo 7.2.1

Escribe la ecuación estándar del círculo con centro $(-2,3)$ y radio $5$ .

Solución

Aquí, $(h,k) = (-2,3)$ y $r = 5$ , así conseguimos

$\begin{array}{rcl} (x-(-2))^2+(y-3)^2 &= &(5)^2 \\ (x+2)^2+(y-3)^2 & = & 25 \end{array}\nonumber$

Ejemplo 7.2.2

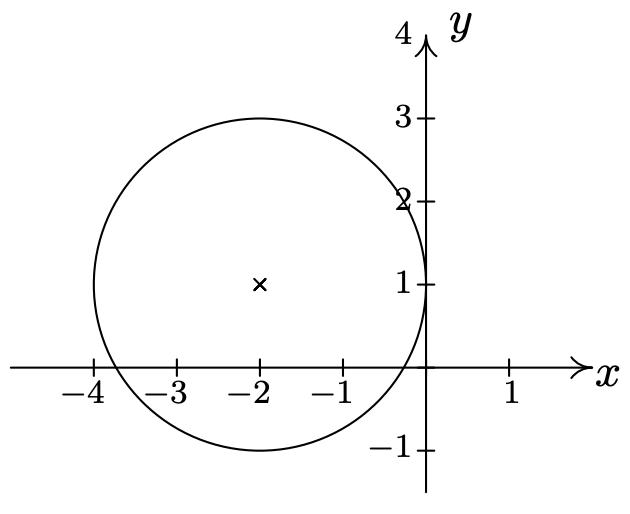
Gráfica $(x+2)^2+(y-1)^2 = 4$ . Encuentra el centro y el radio.

Solución

De la forma estándar de un círculo, la Ecuación 7.1, tenemos que $x + 2$ es $x-h$ , así $h = -2$ y $y - 1$ es $y - k$ así $k = 1$ . Esto nos dice que nuestro centro es $(-2,1)$ . Además, $r^2 = 4$ , entonces $r = 2$ . Así tenemos un círculo centrado en $(-2,1)$ con un radio de $2$ . Graficar nos da

$Screen Shot 2022-04-21 en 4.58.21 PM.png$

Si tuviéramos que expandir la ecuación en el ejemplo anterior y reunir como términos, en lugar de los fácilmente reconocibles $(x+2)^2 + (y-1)^2 = 4$ , estaríamos contendiendo con $x^2 + 4x + y^2 - 2y + 1 = 0.$ Si nos dan tal ecuación, podemos completar el cuadrado en cada una de las variables para ver si se ajusta a la forma dada en la Ecuación 7.1 siguiendo los pasos que se indican a continuación.

Para escribir la ecuación de un círculo en forma estándar

Agrupe las mismas variables en un lado de la ecuación y posicione la constante en el otro lado.
Completar el cuadrado en ambas variables según sea necesario.
Divide ambos lados por el coeficiente de los cuadrados. (Para los círculos, serán los mismos.)

Ejemplo 7.2.3

Completa el cuadrado para encontrar el centro y el radio de $3x^2 - 6x + 3y^2 + 4y -4 = 0$ .

Solución.

$\begin{array}{rclr} 3x^2 - 6x + 3y^2 + 4y -4 & = & 0 & \\ 3x^2 - 6x + 3y^2 + 4y & = & 4 & \mbox{add $4$ to both sides} \\[4pt] 3\left(x^2 - 2x \right) + 3\left(y^2 + \dfrac{4}{3} y\right) & = & 4 & \mbox{factor out leading coefficients} \\ [10pt] 3\left(x^2 - 2x + \underline{1} \right) + 3\left(y^2 + \dfrac{4}{3} y + \underline{\underline{\dfrac{4}{9}}} \right) & = & 4 + 3\underline{(1)} + 3\underline{\underline{\left(\dfrac{4}{9}\right)}} & \mbox{complete the square in $x$, $y$} \\ [10pt] 3(x - 1)^2 + 3\left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{3} & \mbox{factor} \\ [10pt] (x - 1)^2 + \left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{9} & \mbox{divide both sides by $3$}\end{array}\nonumber$

A partir de la Ecuación 7.1, identificamos $x - 1$ como $x - h$ $h = 1$ , así, y $y + \frac{2}{3}$ como $y - k$ , así $k = - \frac{2}{3}$ . De ahí que el centro sea $(h,k) = \left(1, -\frac{2}{3}\right)$ . Además, vemos que $r^2 = \frac{25}{9}$ así es el radio $r = \frac{5}{3}$ .

Es posible obtener ecuaciones como $(x-3)^2 + (y+1)^2 = 0$ o $(x-3)^2 + (y+1)^2 = -1$ , ninguna de las cuales describe un círculo. (¿Ves por qué no?) Se anima al lector a pensar qué puntos, en su caso, se encuentran en las gráficas de estas dos ecuaciones. El siguiente ejemplo utiliza la Fórmula de Punto Medio, Ecuación 1.2, en conjunto con las ideas presentadas hasta el momento en esta sección.

Ejemplo 7.2.4

Escribe la ecuación estándar del círculo que tiene $(-1,3)$ y $(2,4)$ como los puntos finales de un diámetro.

Recordamos que un diámetro de un círculo es un segmento de línea que contiene el centro y dos puntos en el círculo. Trazar los rendimientos de datos dados

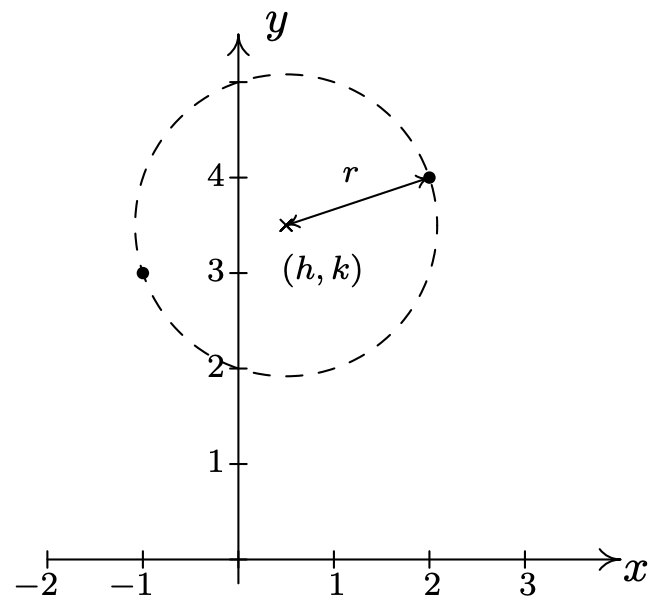
$Screen Shot 2022-04-21 a las 5.18.12 PM.png$

Dado que los puntos dados son puntos finales de un diámetro, sabemos que su punto medio $(h, k)$ es el centro del círculo. La ecuación 1.2 nos da

$\begin{array}{rcl} (h,k) & = & \left( \dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2} \right) \\ [8pt] & = & \left( \dfrac{-1+2}{2}, \dfrac{3+4}{2} \right) \\ [8pt] & = & \left( \dfrac{1}{2}, \dfrac{7}{2} \right) \end{array}\nonumber$

El diámetro del círculo es la distancia entre los puntos dados, por lo que sabemos que la mitad de la distancia es el radio. Por lo tanto,

$\begin{array}{rcl} r & = & \dfrac{1}{2} \sqrt{\left(x_2 - x_1\right)^2+\left(y_2-y_1\right)^2} \\ [8pt] & = & \dfrac{1}{2} \sqrt{(2-(-1))^2+(4-3)^2} \\ [8pt] & = & \dfrac{1}{2} \sqrt{3^2+1^2} \\ [8pt] & = &\dfrac{\sqrt{10}}{2} \end{array}\nonumber$

Por último, ya que $\left( \dfrac{\sqrt{10}}{2} \right)^2 = \dfrac{10}{4}$ , nuestra respuesta se convierte en $\left(x - \dfrac{1}{2} \right)^2 + \left(y - \dfrac{7}{2} \right)^2 =\dfrac{10}{4}$

Cerramos esta sección con el círculo ¹ más importante en todas las matemáticas: el Círculo de Unidades.

Definición 7.2

El Círculo de Unidad es el círculo centrado en $(0,0)$ con un radio de $1$ . La ecuación estándar del Círculo Unitario es $x^2 + y^2 = 1.$

Ejemplo 7.2.5

Encuentra los puntos en el círculo unitario con $y$ coordenada $\dfrac{\sqrt{3}}{2}$ .

Solución

Reemplazamos $y$ con $\dfrac{\sqrt{3}}{2}$ en la ecuación $x^2 + y^2 = 1$ para obtener

$\begin{array}{rcl} x^2 + y^2 & = & 1 \\ x^2 + \left(\dfrac{\sqrt{3}}{2}\right)^2 & = & 1 \\ [13pt] \dfrac{3}{4} + x^2 & = & 1 \\ x^2 & = & \dfrac{1}{4} \\ x & = & \pm \sqrt{\dfrac{1}{4}} \\ [7pt] x & = & \pm \dfrac{1}{2} \end{array}\nonumber$

Nuestras respuestas finales son $\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right)$ y $\left(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right)$ .

7.2.1. Ejercicios

En los Ejercicios 1 - 6, encuentra la ecuación estándar del círculo y luego graficarla.

Centro $(-1, -5)$ , radio $10$
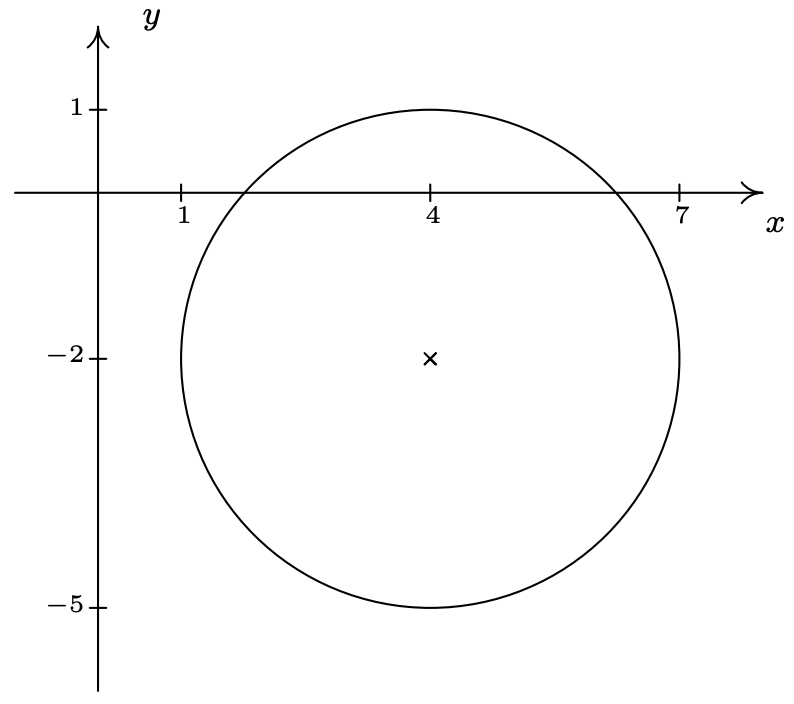
Centro $(4,-2)$ , radio $3$
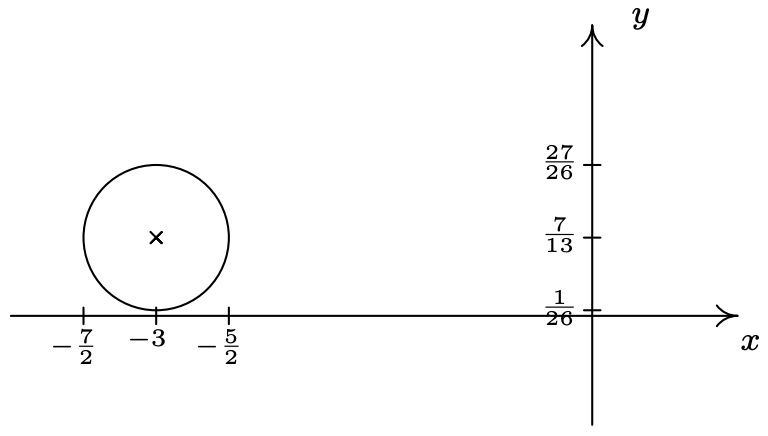
Centro $\left(-3, \frac{7}{13}\right)$ , radio $\frac{1}{2}$
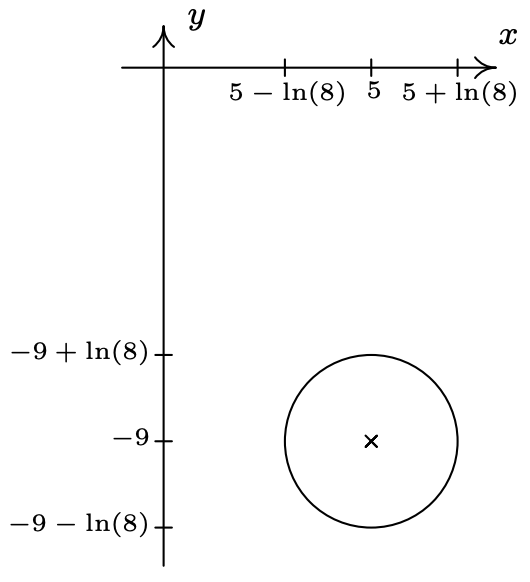
Centro $(5, -9)$ , radio $\ln(8)$
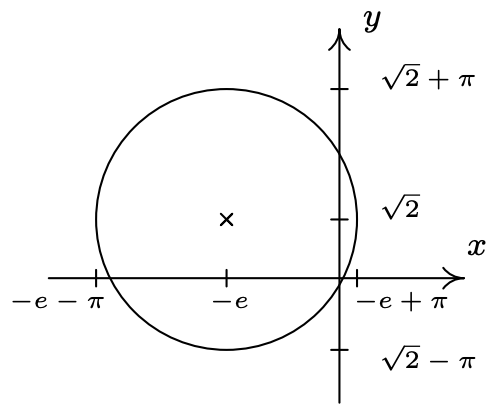
Centro $\left(-e, \sqrt{2}\right)$ , radio $\pi$
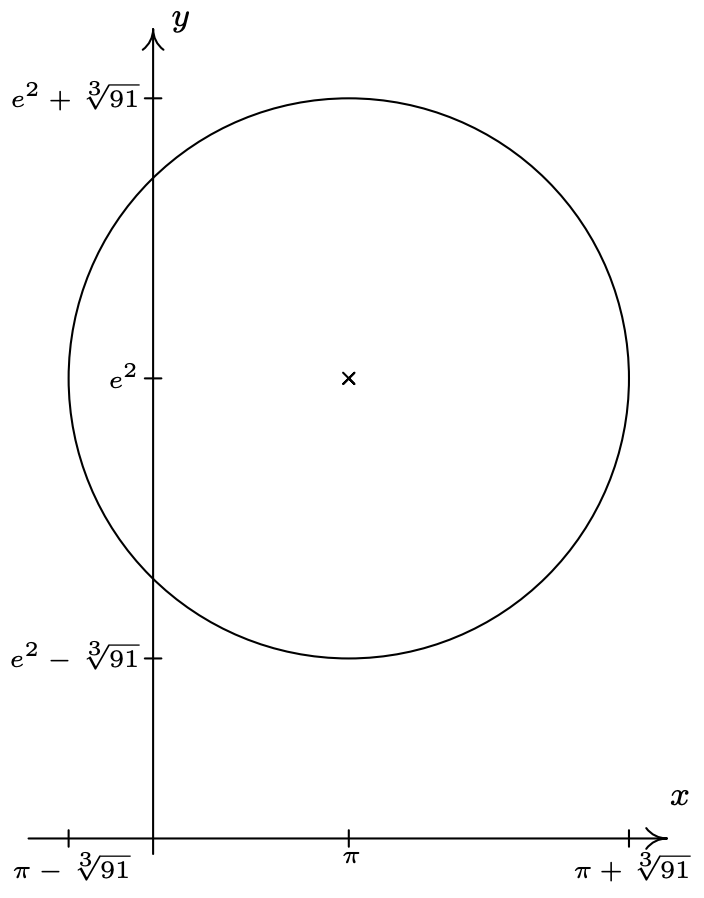
Centro $(\pi, e^{2})$ , radio $\sqrt[3]{91}$

En los Ejercicios 7 - 12, complete el cuadrado para poner la ecuación en forma estándar. Identificar el centro y el radio o explicar por qué la ecuación no representa un círculo.

$x^{2} - 4x + y^{2} + 10y = -25$
$-2x^{2} - 36x - 2y^{2} - 112 = 0$
$x^2+y^2+8x-10y -1 =0$
$x^2+y^2+5x-y-1=0$
$4x^{2} + 4y^{2} - 24y + 36 = 0$
$x^{2} + x + y^{2} - \frac{6}{5}y = 1$

En los Ejercicios 13 - 16, encuentra la ecuación estándar del círculo que satisface los criterios dados.

centro $(3, 5)$ , pasa a través $(-1, -2)$
centro $(3, 6)$ , pasa a través $(-1, 4)$
puntos finales de un diámetro: $(3,6)$ y $(-1,4)$
puntos finales de un diámetro: $\left( \frac{1}{2}, 4\right)$ , $\left(\frac{3}{2}, -1\right)$
La Rueda Gigante en Cedar Point es un círculo con 128 pies de diámetro que se asienta sobre una plataforma de 8 pies de altura haciendo que su altura total sea de 136 pies. ² Encuentra una ecuación para la rueda asumiendo que su centro se encuentra en el $y$ eje -y que el suelo es el $x$ eje -eje.
Verificar que los siguientes puntos se encuentran en el Círculo de Unidad: $(\pm 1, 0)$ , $(0, \pm 1)$ , $\left(\pm \frac{\sqrt{2}}{2}, \pm \frac{\sqrt{2}}{2}\right)$ , $\left(\pm \frac{1}{2}, \pm \frac{\sqrt{3}}{2}\right)$ y $\left(\pm \frac{\sqrt{3}}{2}, \pm \frac{1}{2}\right)$
Discuta con sus compañeros de clase cómo obtener la ecuación estándar de un círculo, Ecuación 7.1, a partir de la ecuación del Círculo de Unidad, $x^2+y^2=1$ utilizando las transformaciones discutidas en la Sección 1.7. (Así, cada círculo está a solo unas transformaciones de distancia del Círculo de Unidad.)
Encuentra una ecuación para la función representada gráficamente por la mitad superior del Círculo de Unidades. Explique cómo las transformaciones de la Sección 1.7 pueden ser utilizadas para producir una función cuya gráfica sea la parte superior o inferior de un círculo arbitrario.
Encuentra una función uno a uno cuya gráfica sea la mitad de un círculo. (Pista: Piense poco a poco.)

7.2.2. RESPUESTAS

$(x + 1)^{2} + (y + 5)^{2} = 100$
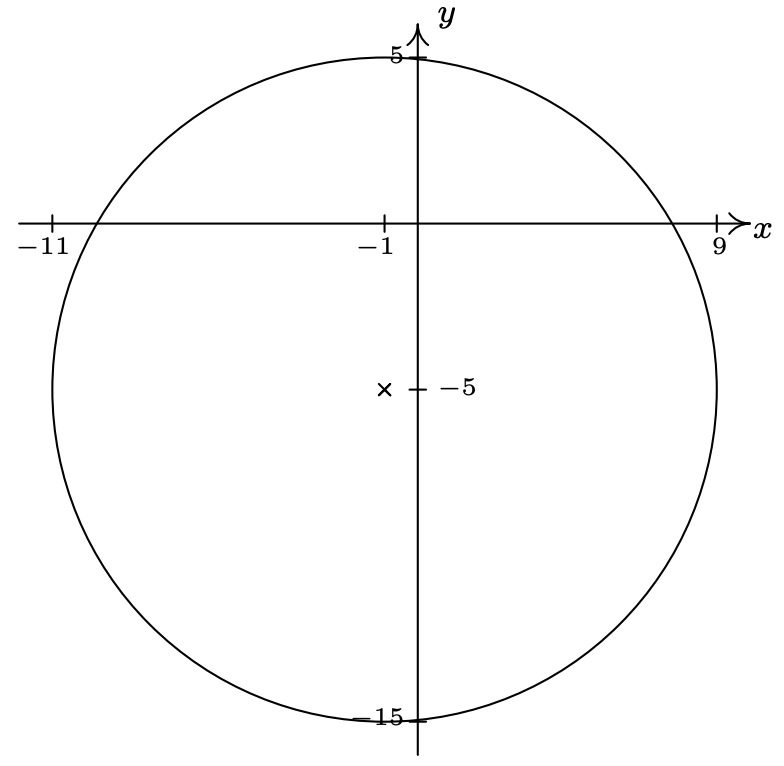
$Screen Shot 2022-04-28 a las 3.12.27 PM.png$
$(x-4)^2+(y+2)^2 = 9$
$Screen Shot 2022-04-28 en 3.13.04 PM.png$
$\left(x + 3\right)^{2} + \left(y - \frac{7}{13}\right)^{2} = \frac{1}{4}$
$Screen Shot 2022-04-28 a las 3.14.31 PM.png$
$(x - 5)^{2} + (y + 9)^{2} = (\ln(8))^{2}$
$Screen Shot 2022-04-28 a las 3.16.15 PM.png$
$(x + e)^{2} + \left(y - \sqrt{2} \right)^{2} = \pi^{2}$
$Screen Shot 2022-04-28 a las 3.16.48 PM.png$
$\left(x - \pi \right)^{2} + \left(y - e^{2}\right)^{2} = 91^{\frac{2}{3}}$
$Screen Shot 2022-04-28 a las 3.17.19 PM.png$
$(x - 2)^{2} + (y + 5)^{2} = 4$
Centro $(2, -5)$ , radio $r = 2$
$(x + 9)^{2} + y^{2} = 25$
Centro $(-9, 0)$ , radio $r = 5$
$(x+4)^2 + (y-5)^2 = 42$
Centro $(-4,5)$ , radio $r = \sqrt{42}$
$\left(x + \frac{5}{2}\right)^2 + \left(y - \frac{1}{2}\right)^2 = \frac{30}{4}$
Centro $\left( -\frac{5}{2}, \frac{1}{2}\right)$ , radio $r = \frac{\sqrt{30}}{2}$
$x^{2} + (y - 3)^{2} = 0$
Esto no es un círculo.
$\left(x + \frac{1}{2}\right)^{2} + \left(y - \frac{3}{5}\right)^{2} = \frac{161}{100}$
Centro $\left(-\frac{1}{2}, \frac{3}{5}\right)$ , radio $r = \frac{\sqrt{161}}{10}$
$(x - 3)^{2} + (y - 5)^{2} = 65$
$(x-3)^2+(y-6)^2 = 20$
$(x-1)^2 + (y-5)^2 = 5$
$(x-1)^2 + \left(y - \frac{3}{2}\right)^2 = \frac{13}{2}$
$x^{2} + (y - 72)^{2} = 4096$