8.3: Aritmética Matricial

En la Sección 8.2, se utilizó una clase especial de matrices, las matrices aumentadas, para ayudarnos a resolver sistemas de ecuaciones lineales. En esta sección, estudiamos las matrices como objetos matemáticos por su propia cuenta, temporalmente divorciados de los sistemas de ecuaciones lineales. Para hacerlo convenientemente se requiere algo más de notación. Cuando escribimos\(A = \left[ a_{ij} \right]_{m \times n}\), queremos decir\(A\) es una\(n\) matriz\(m\) por ¹ y\(a_{ij}\) es la entrada que se encuentra en la fila\(i\) th y\(j\) th columna. Esquemáticamente, tenemos

Con esta nueva notación podemos definir lo que significa que dos matrices sean iguales.

Definición 8.6.

Igualdad Matriz: Se dice que dos matrices son iguales si son del mismo tamaño y sus entradas correspondientes son iguales. Más específicamente, si\(A =\left[a_{ij}\right]_{m \times n}\) y\(B =\left[b_{ij}\right]_{p \times r}\), escribimos\(A=B\) siempre

1. \(m=p\)y\(n=r\)
2. \(a_{ij} = b_{ij}\)para todos\(1 \leq i \leq m\) y para todos\(1 \leq j \leq n\).

Esencialmente, dos matrices son iguales si son del mismo tamaño y tienen los mismos números en los mismos puntos. ² Por ejemplo, las dos\(2 \times 3\) matrices a continuación son, a pesar de las apariencias, iguales.

\[\left[ \begin{array}{rrr} 0 & -2 & 9 \\ 25 & 117 & -3 \\ \end{array} \right] = \left[ \begin{array}{rrr} \ln(1) & \sqrt[3]{-8} & e^{2\ln(3)} \\ 125^{2/3} & 3^{2} \cdot 13 & \log(0.001) \end{array} \right]\nonumber\]

Ahora que tenemos una comprensión acordada de lo que significa que dos matrices se igualen entre sí, podemos comenzar a definir operaciones aritméticas sobre matrices. Nuestra primera operación es la adición.

Definición 8.7.

Adición de Matriz: Dadas dos matrices del mismo tamaño, la matriz obtenida sumando las entradas correspondientes de las dos matrices se denomina la suma de las dos matrices. Más específicamente, si\(A =\left[a_{ij}\right]_{m \times n}\) y\(B =\left[b_{ij}\right]_{m \times n}\), definimos\[A + B = \left[a_{ij}\right]_{m \times n} + \left[b_{ij}\right]_{m \times n} = \left[ a_{ij} + b_{ij} \right]_{m \times n}\nonumber\]

A modo de ejemplo, considere la suma a continuación.

\[\left[ \begin{array}{rr}2 & 3 \\ 4 & -1 \\ 0 & -7 \\ \end{array} \right] + \left[ \begin{array}{rr} -1 & 4 \\ -5 & -3 \\ 8 & 1 \\ \end{array} \right] = \left[ \begin{array}{rr} 2 + (-1) & 3+4 \\ 4+(-5) & (-1)+(-3) \\ 0+8 & (-7)+ 1 \\ \end{array} \right] = \left[ \begin{array}{rr} 1 & 7 \\ -1 & -4 \\ 8 & -6 \\ \end{array} \right]\nonumber\]

Vale la pena el tiempo del lector para pensar qué habría pasado si hubiéramos invertido el orden de los summands anteriores. Como era de esperar, llegamos a la misma respuesta. En general,\(A+B = B+A\) para matrices\(A\) y\(B\), siempre que sean del mismo tamaño para que la suma se defina en primer lugar. Esta es la propiedad conmutativa de la adición matricial. Para ver por qué esto es cierto en general, apelamos a la definición de adición matricial. Dado\(A =\left[a_{ij}\right]_{m \times n}\) y\(B =\left[b_{ij}\right]_{m \times n}\),\[A + B = \left[a_{ij}\right]_{m \times n} + \left[b_{ij}\right]_{m \times n} = \left[ a_{ij} + b_{ij} \right]_{m \times n} = \left[ b_{ij} + a_{ij} \right]_{m \times n} = \left[b_{ij}\right]_{m \times n} + \left[a_{ij}\right]_{m \times n} =B+A\nonumber\] donde la segunda igualdad es la definición de\(A+B\), la tercera igualdad sostiene por la ley conmutativa de adición de número real, y la cuarta igualdad es la definición de\(B+A\). En otras palabras, la adición de matriz es conmutativa porque la adición de números reales lo es. Un argumento similar muestra también la propiedad asociativa de la adición matricial, heredada a su vez de la ley asociativa de la adición de números reales. Específicamente, para matrices\(A\),\(B\), y\(C\) del mismo tamaño,\((A+B)+C = A+(B+C)\). Es decir, al agregar más de dos matrices, no importa cómo se agrupen. Esto significa que podemos escribir\(A+B+C\) sin paréntesis y no hay ambigüedad en cuanto a lo que esto significa. ³ Estas propiedades y más se resumen en el siguiente teorema.

Teorema 8.3.

Propiedades de Matrix Addition

• Propiedad conmutativa: Para todas las\(m \times n\) matrices,\(A + B = B + A\)
• Propiedad asociativa: Para todas las\(m \times n\) matrices,\((A + B) + C = A + (B + C)\)
• Propiedad de Identidad: Si\(0_{m \times n}\) es la\(m \times n\) matriz cuyas entradas son todas\(0\), entonces\(0_{m \times n}\) se llama la identidad\(m \times n\) aditiva y para todas las\(m \times n\) matrices\(A\)\[A + 0_{m \times n} = 0_{m \times n} + A = A\nonumber\]
• Propiedad inversa: Para cada\(m \times n\) matriz dada\(A\), hay una matriz única denotada\(-A\) llamada inversa aditiva de\(A\) tal que\[A + (-A) = (-A) + A = 0_{m \times n}\nonumber\]

La propiedad de identidad se verifica fácilmente recurriendo a la definición de adición de matriz; así como el número\(0\) es la identidad aditiva para números reales, la matriz compuesta por todos\(0\) hace el mismo trabajo para matrices. Para establecer la propiedad inversa, dada una matriz\(A=\left[a_{ij}\right]_{m \times n}\), estamos buscando una matriz para\(B = \left[b_{ij}\right]_{m \times n}\) que\(A + B = 0_{m \times n}\). Por la definición de adición matricial, debemos tener eso\(a_{ij} + b_{ij} = 0\) para todos\(i\) y\(j\). Resolviendo, obtenemos\(b_{ij} = -a_{ij}\). De ahí que dada una matriz\(A\), su inversa aditiva, que llamamos\(-A\), sí existe y es única y, además, viene dada por la fórmula:\(-A = \left[ - a_{ij}\right]_{m \times n}\). El largo y corto de esto es: para obtener la inversa aditiva de una matriz, tomar inversas aditivas de cada una de sus entradas. Con el concepto de inversa aditiva bien en la mano, ahora podemos discutir qué se entiende por restar matrices. Quizás recuerdes de la aritmética que\(a - b = a+(-b)\); es decir, la resta se define como 'sumar lo opuesto (inverso) '. Extendemos este concepto a las matrices. Para dos matrices\(A\) y\(B\) del mismo tamaño, definimos\(A-B = A + (-B)\). A nivel de entradas, esto equivale a

\[A-B = A + (-B) = \left[a_{ij}\right]_{m \times n} + \left[-b_{ij}\right]_{m \times n} = \left[a_{ij} + \left(-b_{ij}\right) \right]_{m \times n} = \left[a_{ij} - b_{ij} \right]_{m \times n}\nonumber\]

Así, para restar dos matrices de igual tamaño, restamos sus entradas correspondientes. ¿Sorprendido?

Nuestra siguiente tarea es definir lo que significa multiplicar una matriz por un número real. Pensando en la aritmética, tal vez recuerdes que la multiplicación, al menos por un número natural, puede pensarse como 'suma rápida'. Por ejemplo,\(2+2+2 = 3 \cdot 2\). Sabemos por álgebra ⁴ que\(3x = x + x + x\), por lo que parece natural que dada una matriz\(A\), definimos\(3A = A + A + A\). Si\(A =\left[a_{ij}\right]_{m \times n}\), tenemos\[3A = A + A + A = \left[a_{ij}\right]_{m \times n} + \left[a_{ij}\right]_{m \times n} + \left[a_{ij}\right]_{m \times n} = \left[a_{ij} + a_{ij} + a_{ij} \right]_{m \times n} = \left[ 3a_{ij}\right]_{m \times n}\nonumber\] En otras palabras, multiplicar la matriz de esta manera por\(3\) es lo mismo que multiplicar cada entrada por\(3\). Esto nos lleva a la siguiente definición.

Definición 8.8.

Escalar ^a Multiplicación: Definimos el producto de un número real y una matriz para ser la matriz obtenida multiplicando cada una de sus entradas por dicho número real. Más específicamente, si\(k\) es un número real y\(A = \left[a_{ij}\right]_{m \times n}\), definimos\[kA = k\left[a_{ij}\right]_{m \times n} = \left[ka_{ij}\right]_{m \times n}\nonumber\]

---

^a La palabra 'escalar' aquí se refiere a números reales. 'Multiplicación escalar' en este contexto significa que estamos multiplicando una matriz por un número real (un escalar).

Uno bien puede preguntarse por qué se usa la palabra 'escalar' para 'número real'. Tiene todo que ver con factores de 'escalado'. ⁵ Un punto\(P(x,y)\) en el plano puede ser representado por su matriz de posición,\(P\):

\[(x,y) \leftrightarrow P = \left[ \begin{array}{r} x \\ y \\ \end{array} \right]\nonumber\]

Supongamos que tomamos el punto\((-2,1)\) y multiplicamos su matriz de posición por\(3\). Tenemos\[3P = 3 \left[ \begin{array}{r} -2 \\ 1 \\ \end{array} \right] = \left[ \begin{array}{r} 3(-2) \\ 3(1) \\ \end{array} \right] = \left[ \begin{array}{r} -6 \\ 3 \\ \end{array} \right]\nonumber\] lo que corresponde al punto\((-6,3)\). Podemos imaginarnos tomando\((-2,1)\) a de esta\((-6,3)\) manera como una dilatación por un factor de tanto\(3\) en la dirección horizontal como en la vertical. Hacer esto a todos los puntos\((x,y)\) del plano, por lo tanto, tiene el efecto de magnificar (escalar) el plano por un factor de\(3\).

Al igual que la adición de matrices, la multiplicación escalar hereda muchas propiedades de la aritmética de números reales. A continuación resumimos estas propiedades.

Teorema 8.4. Propiedades de la Multiplicación Escalar

• Propiedad Asociativa: Para cada\(m \times n\) matriz\(A\) y escalares\(k\) y\(r\),\((kr)A = k(rA)\).
• Identidad Propiedad: Para todas las\(m \times n\) matrices\(A\),\(1A = A\).
• Propiedad inversa aditiva: Para todas las\(m \times n\) matrices\(A\),\(-A = (-1)A\).
• Propiedad Distributiva de Multiplicación Escalar sobre Adición Escalar: Para cada\(m \times n\) matriz\(A\) y escalares\(k\) y\(r\),\[(k+r)A = kA + rA\nonumber\]
• Propiedad Distributiva de Multiplicación Escalar sobre Adición de Matriz: Para todas\(m \times n\) las matrices\(A\) y\(B\) escalares\(k\),\[k(A+B) = kA + kB\nonumber\]
• Zero Product Property: Si\(A\) es una\(m \times n\) matriz y\(k\) es un escalar, entonces\[kA = 0_{m \times n} \quad \text{if and only if} \quad k=0 \quad \text{or} \quad A = 0_{m \times n}\nonumber\]

Al igual que con los otros resultados de esta sección, el Teorema 8.4 se puede probar utilizando las definiciones de multiplicación escalar y adición de matriz. Por ejemplo, para probar eso\(k(A+B) = kA + kB\) para un escalar\(k\) y\(m \times n\) matrices\(A\) y\(B\), empezamos por sumar\(A\) y\(B\), luego multiplicando por\(k\) y viendo como eso se compara con la suma de\(kA\) y\(kB\). \[k(A+B) = k \left(\left[a_{ij}\right]_{m \times n} + \left[b_{ij}\right]_{m \times n}\right) = k \left[a_{ij} + b_{ij} \right]_{m \times n} = \left[k \left(a_{ij}+b_{ij}\right)\right]_{m \times n} = \left[ka_{ij} + kb_{ij}\right]_{m \times n}\nonumber\]

En cuanto\(kA + kB\) a, tenemos

\[kA + kB = k\left[a_{ij}\right]_{m \times n}+k\left[b_{ij}\right]_{m \times n} = \left[ka_{ij}\right]_{m \times n}+\left[kb_{ij}\right]_{m \times n} = \left[ka_{ij} + kb_{ij}\right]_{m \times n} \, \, \checkmark\nonumber\]

que establece la propiedad. Las propiedades restantes se dejan al lector. Las propiedades en los Teoremas 8.3 y 8.4 establecen un sistema algebraico que nos permite tratar matrices y escalares más o menos como haríamos números y variables reales, como ilustra el siguiente ejemplo.

Ejemplo 8.3.1

Resolver para la matriz\(A\):\(3A - \left(\left[ \begin{array}{rr} 2 & -1 \\ 3 & 5 \\ \end{array}\right] + 5A\right) = \left[ \begin{array}{rr} -4 & 2 \\ 6 & -2 \\ \end{array}\right] + \dfrac{1}{3} \left[ \begin{array}{rr} 9 & 12 \\ -3 & 39 \\ \end{array}\right]\) usando las definiciones y propiedades de la aritmética matricial.

Solución

\[\begin{array}{rcl} 3A - \left(\left[ \begin{array}{rr} 2 & -1 \\ 3 & 5 \\ \end{array}\right] + 5A\right) & = & \left[ \begin{array}{rr} -4 & 2 \\ 6 & -2 \\ \end{array}\right] + \dfrac{1}{3} \left[ \begin{array}{rr} 9 & 12 \\ -3 & 39 \\ \end{array}\right] \\ 3A + \left\{-\left(\left[ \begin{array}{rr} 2 & -1 \\ 3 & 5 \\ \end{array}\right] + 5A \right)\right\} & = & \left[ \begin{array}{rr} -4 & 2 \\ 6 & -2 \\ \end{array}\right] + \left[ \begin{array}{rr} \left(\frac{1}{3}\right)(9) & \left(\frac{1}{3}\right)(12) \\[2pt] \left(\frac{1}{3}\right)(-3) & \left(\frac{1}{3}\right)(39) \\ \end{array}\right] \\ 3A + (-1)\left(\left[ \begin{array}{rr} 2 & -1 \\ 3 & 5 \\ \end{array}\right] + 5A \right) & = & \left[ \begin{array}{rr} -4 & 2 \\ 6 & -2 \\ \end{array}\right] + \left[ \begin{array}{rr} 3 & 4 \\ -1 & 13 \\ \end{array}\right] \\ 3A + \left\{ (-1)\left[ \begin{array}{rr} 2 & -1 \\ 3 & 5 \\ \end{array}\right] + (-1)(5A)\right \} & = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] \\ 3A + (-1)\left[ \begin{array}{rr} 2 & -1 \\ 3 & 5 \\ \end{array}\right] + (-1)(5A) & = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] \\ 3A + \left[ \begin{array}{rr} (-1)(2) & (-1)(-1) \\ (-1)(3) & (-1)(5) \\ \end{array}\right] + ((-1)(5))A & = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] \\ 3A + \left[ \begin{array}{rr} -2 & 1 \\ -3 & -5 \\ \end{array}\right] + (-5)A & = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] \\ 3A + (-5)A+ \left[ \begin{array}{rr} -2 & 1 \\ -3 & -5 \\ \end{array}\right]& = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] \\ (3+ (-5))A+ \left[ \begin{array}{rr} -2 & 1 \\ -3 & -5 \\ \end{array}\right] + \left(-\left[ \begin{array}{rr} -2 & 1 \\ -3 & -5 \\ \end{array}\right] \right)& = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] + \left(-\left[ \begin{array}{rr} -2 & 1 \\ -3 & -5 \\ \end{array}\right] \right) \\ (-2)A+ 0_{2 \times 2} & = & \left[ \begin{array}{rr} -1 & 6 \\ 5 & 11 \\ \end{array}\right] -\left[ \begin{array}{rr} -2 & 1 \\ -3 & -5 \\ \end{array}\right] \\ (-2)A & = & \left[ \begin{array}{rr} -1 - (-2) & 6 - 1 \\ 5 - (-3) & 11 - (-5) \\ \end{array}\right] \\ (-2)A & = & \left[ \begin{array}{rr} 1 & 5 \\ 8 & 16 \\ \end{array}\right] \\ \left(-\frac{1}{2}\right)\left((-2)A\right) & = & -\frac{1}{2} \left[ \begin{array}{rr} 1 & 5 \\ 8 & 16 \\ \end{array}\right] \\ \left(\left(-\frac{1}{2}\right)(-2)\right)A & = & \left[ \begin{array}{rr} \left(-\frac{1}{2}\right)(1) & \left(-\frac{1}{2}\right)(5) \\[2pt] \left(-\frac{1}{2}\right)(8) & \left(-\frac{1}{2}\right)(16) \\ \end{array}\right] \\ 1 A & = & \left[ \begin{array}{rr} -\frac{1}{2} & -\frac{5}{2} \\[2pt] -4 & -\frac{16}{2} \\ \end{array}\right] \\ A & = & \left[ \begin{array}{rr} -\frac{1}{2} & -\frac{5}{2} \\[2pt] -4 & -8 \\ \end{array}\right] \\ \end{array}\nonumber\]Se anima al lector a verificar nuestra respuesta en la ecuación original.

Si bien la solución al ejemplo anterior está escrita con insoportante detalle, en la práctica se omiten muchos de los pasos anteriores. Hemos explicado cada paso en este ejemplo para animar al lector a justificar cada paso usando las definiciones y propiedades que hemos establecido hasta ahora para la aritmética matricial. Se anima al lector a resolver la ecuación en el Ejemplo 8.3.1 como lo harían con cualquier otra ecuación lineal, por ejemplo:\(3a-(2+5a)=-4+\frac{1}{3}(9)\).

Ahora volvemos nuestra atención a la multiplicación matricial, es decir, multiplicar una matriz por otra matriz. Con base en la tendencia 'no sorpresas' hasta el momento de la sección, puede esperar que para multiplicar dos matrices, deben ser del mismo tamaño y encuentre el producto multiplicando las entradas correspondientes. Si bien este tipo de producto es utilizado en otras áreas de las matemáticas, ⁶ definimos la multiplicación matricial para servirnos en la resolución de sistemas de ecuaciones lineales. Para ello, comenzamos definiendo el producto de una fila y una columna. Motivamos la definición general con un ejemplo. Considera las dos matrices\(A\) y\(B\) abajo.

\[\begin{array}{cc} A = \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right] & B = \left[\begin{array}{rrrr} 3 & \hphantom{-}1 & 2 & -8 \\ 4 & 8 & -5 & 9 \\ 5 & 0 & -2 & -12 \\ \end{array} \right] \end{array}\nonumber\]

Dejar\(R1\) denotar la primera fila de\(A\) y\(C1\) denotar la primera columna de\(B\). Para encontrar el 'producto' de\(R1\) con\(C1\), denotado\(R1 \cdot C1\), primero encontramos el producto de la primera entrada\(R1\) y la primera entrada en\(C1\). A continuación, agregamos a eso el producto de la segunda entrada en\(R1\) y la segunda entrada en\(C1\). Por último, tomamos esa suma y a eso le sumamos el producto de la última entrada en\(R1\) y la última entrada en\(C1\). Usando notación de entrada,\(R1 \cdot C1 = a_{11}b_{11} + a_{12}b_{21}+a_{13}b_{31} = (2)(3) + (0)(4) + (-1)(5) = 6 + 0 + (-5) = 1\). Podemos visualizar esto esquemáticamente de la siguiente manera

\[\left[\begin{array}{rrr} \rowcolor[gray]{0.9} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right] \left[\begin{array}{>{\columncolor[gray]{0.9}}rrrr} 3 & \hphantom{-}1 & 2 & -8 \\ 4 & 8 & -5 & 9 \\ 5 & 0 & -2 & -12 \\ \end{array} \right]\nonumber\]

\[\begin{array}{ccccc} \underbrace{\begin{array}{rl} \stackrel{\xrightarrow{\hspace{.75in}}}{\begin{array}{ccc} \fbox{2} & \hphantom{-}0 & -1 \end{array}} & \left. \begin{array}{c} \fbox{3} \\ 4 \\ 5 \\ \end{array} \right\downarrow \\ \end{array}} & & \underbrace{\begin{array}{rl} \stackrel{\xrightarrow{\hspace{.75in}}}{\begin{array}{ccc} 2 & \hphantom{-}\fbox{0} & -1 \end{array}} & \left. \begin{array}{c} 3 \\ \fbox{4} \\ 5 \\ \end{array} \right\downarrow \\\end{array}} & & \underbrace{\begin{array}{rl} \stackrel{\xrightarrow{\hspace{.75in}}}{\begin{array}{ccc} 2 & \hphantom{-}0 & \fbox{$-1$} \end{array}} & \left. \begin{array}{c} 3 \\ 4 \\ \fbox{5} \\ \end{array} \right\downarrow \\ \end{array}} \\ a_11b_11 & + & a_12b_21 & + & a_13b_31 \\ (2)(3) & + &(0)(4)& + & (-1)(5) \\ \end{array}\nonumber\]

Para encontrar\(R2 \cdot C3\) donde\(R2\) denota la segunda fila de\(A\) y\(C3\) denota la tercera columna de\(B\), procedemos de manera similar. Comenzamos por encontrar el producto de la primera entrada de\(R2\) con la primera entrada en\(C3\) luego agregarle el producto de la segunda entrada adentro\(R2\) con la segunda entrada adentro\(C3\), y así sucesivamente. Usando notación de entrada, tenemos\(R2 \cdot C3 = a_{21}b_{13} + a_{22}b_{23} + a_{23}b_{33} = (-10)(2) + (3)(-5) + (5)(-2) = -45\). Esquemáticamente,

\[\left[\begin{array}{rrr} 2 & 0 & -1 \\ \rowcolor[gray]{0.9} -10 & \hphantom{-}3 & 5 \\ \end{array} \right] \left[\begin{array}{rr>{\columncolor[gray]{0.9}}rr} 3 & \hphantom{-}1 & 2 & -8 \\ 4 & 8 & -5 & 9 \\ 5 & 0 & -2 & -12 \\ \end{array} \right]\nonumber\]

\[\begin{array}{ccccc} \underbrace{\begin{array}{rl} \stackrel{\xrightarrow{\hspace{.75in}}}{\begin{array}{ccc} \fbox{$-10$} & 3 & 5 \end{array}} & \left. \begin{array}{c} \fbox{\hphantom{$-$}2} \\ -5 \\ -2 \\ \end{array} \right\downarrow \\ \end{array}} & & \underbrace{\begin{array}{rl} \stackrel{\xrightarrow{\hspace{.75in}}}{\begin{array}{ccc} -10 & \fbox{3} & 5 \end{array}} & \left. \begin{array}{c} \hphantom{-}2 \\ \fbox{$-5$} \\ -2 \\ \end{array} \right\downarrow \\\end{array}} & & \underbrace{\begin{array}{rl} \stackrel{\xrightarrow{\hspace{.75in}}}{\begin{array}{ccc} -10 & 3 & \fbox{$5$} \end{array}} & \left. \begin{array}{c} \hphantom{-}2 \\ -5 \\ \fbox{$-2$} \\ \end{array} \right\downarrow \\ \end{array}} \\ a_21b_13= (-10)(2) = -20 & + & a_22b_23 = (3)(-5) = -15 & + & a_23b_33 = (5)(-2) = -10 \\ \end{array}\nonumber\]

Generalizando este proceso, tenemos la siguiente definición.

Definición 8.9.

Producto de una Fila y una Columna: Supongamos\(A = [a_{ij}]_{m \times n}\) y\(B = [b_{ij}]_{n \times r}\). Dejar\(Ri\) denotar la fila\(i\) th de\(A\) y dejar\(Cj\) denotar la\(j\) th columna de\(B\). El producto de\(R_{i}\) y\(C_{j}\), denotado\(R_{i} \cdot C_{j}\) es el número real definido por\[Ri \cdot Cj = a_{i\mbox{\tiny$1$}}b_1$}j} + a_{i\mbox{\tiny$2b_{\mbox{\tiny$2$}j} + \ldots a_{in}b_{nj}\nonumber\]

Tenga en cuenta que para multiplicar una fila por una columna, el número de entradas en la fila debe coincidir con el número de entradas en la columna. Ahora estamos en condiciones de definir la multiplicación matricial.

Definición 8.10.

Multiplicación Matriz: Supongamos\(A = [a_{ij}]_{m \times n}\) y\(B = [b_{ij}]_{n \times r}\). Dejar\(Ri\) denotar la fila\(i\) th de\(A\) y dejar\(Cj\) denotar la\(j\) th columna de\(B\). El producto de\(A\) y\(B\), denotado\(AB\), es la matriz definida por\[AB = \left[ Ri \cdot Cj \right]_{m \times r}\nonumber\]

es decir

\[AB = \left[ \begin{array}{cccc} R1 \cdot C1 & R1 \cdot C2 & \ldots & R1 \cdot Cr \\ R2 \cdot C1 & R2 \cdot C2 & \ldots & R2 \cdot Cr \\ \vdots & \vdots & & \vdots \\ Rm \cdot C1 & Rm \cdot C2 & \ldots & Rm \cdot Cr \\ \end{array} \right]\nonumber\]

Hay una serie de sutilezas en la Definición 8.10 que justifican una inspección más cercana. En primer lugar, la Definición 8.10 nos dice que la\(ij\) -entrada de un producto de matriz\(AB\) es la fila\(i\) th de\(A\) veces la\(j\) ésima columna de\(B\). Para que esto se defina, el número de entradas en las filas de\(A\) debe coincidir con el número de entradas en las columnas de\(B\). Esto significa que el número de columnas de\(A\) debe coincidir con ⁷ el número de filas de\(B\). Es decir, para multiplicar\(A\) tiempos\(B\), la segunda dimensión de\(A\) debe coincidir con la primera dimensión de\(B\), razón por la cual en la Definición 8.10,\(A_{m \times \underline{n}}\) se está multiplicando por una matriz\(B_{\underline{n} \times r}\). Además, la matriz de productos\(AB\) tiene tantas filas como\(A\) y tantas columnas de\(B\). Como resultado, al multiplicar una matriz\(A_{\underline{m} \times n}\) por una matriz\(B_{n \times \underline{r}}\), el resultado es la matriz\(AB_{\underline{m} \times \underline{r}}\). Volviendo a nuestras matrices de ejemplo a continuación, vemos que\(A\) es una\(2 \times \underline{3}\) matriz y\(B\) es una\(\underline{3} \times 4\) matriz. Esto significa que la matriz del producto\(AB\) está definida y será una\(2 \times 4\) matriz.

\[\begin{array}{cc} A = \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right] & B = \left[\begin{array}{rrrr} 3 & \hphantom{-}1 & 2 & -8 \\ 4 & 8 & -5 & 9 \\ 5 & 0 & -2 & -12 \\ \end{array} \right] \end{array}\nonumber\]

Usando\(Ri\) para denotar la fila\(i\) th de\(A\) y\(Cj\) para denotar la\(j\) ésima columna de\(B\), formamos de\(AB\) acuerdo con la Definición 8.10.

\[\begin{array}{rclcl} AB & = & \left[\begin{array}{rrrr} R1 \cdot C1 & R1 \cdot C2 & R1 \cdot C3 & R1 \cdot C4 \\ R2 \cdot C1 & R2 \cdot C2 & R2 \cdot C3 & R2 \cdot C4 \\ \end{array} \right] & = & \left[\begin{array}{rrrr} 1 & \hphantom{-}2 & 6 & -4 \\ 7 & 14 & -45 & 47 \\ \end{array} \right] \\ \end{array}\nonumber\]

Obsérvese que el producto no\(BA\)\(B\) está definido, ya que\(A\) es una\(3 \times \underline{4}\)\(\underline{2} \times 3\) matriz mientras que es una matriz;\(B\)\(A\) tiene más columnas que filas, y así no es posible multiplicar una fila de\(B\) por una columna de\(A\). Incluso cuando las dimensiones de\(A\) y\(B\) son compatibles de tal manera que\(AB\) y ambos\(BA\) están definidos, el producto\(AB\) y\(BA\) no son necesariamente iguales. ⁸ En otras palabras, no\(AB\) puede ser igual\(BA\). Aunque no existe una propiedad conmutativa de la multiplicación matricial en general, varias otras propiedades numéricas reales son heredadas por la multiplicación matricial, como se ilustra en nuestro siguiente teorema.

Teorema 8.5

Propiedades de la Multiplicación Matriz Let\(A\),\(B\) y\(C\) ser matrices tales que todos los productos de la matriz a continuación se definen y dejan\(k\) ser un número real.

• Propiedad asociativa de la multiplicación matricial:\((AB)C = A(BC)\)
• Propiedad Asociativa con Multiplicación Escalar:\(k(AB) = (kA)B = A(kB)\)
• Propiedad de Identidad: Para un número natural\(k\), la matriz de\(k \times k\) identidad, denotada\(I_{k}\), se define por\(I_{k} = \left[d_{ij} \right]_{k \times k}\) donde\[d_{ij} = \left\{ \begin{array}{rl} 1, & \text{if $i=j$} \\ 0, & \text{otherwise} \\ \end{array} \right.\nonumber\] Para todas las\(m \times n\) matrices,\(I_{m}A = AI_{n} = A\).
• Propiedad Distributiva de Multiplicación Matricial sobre Adición Matricial:\[A(B \pm C) = AB \pm AC \mbox{ and } (A \pm B)C = AC \pm BC\nonumber\]

La única propiedad del Teorema 8.5 que pide mayor investigación es, sin duda, la identidad multiplicativa. [maindiagonal] Las entradas en una matriz donde\(i=j\) comprenden lo que se llama la diagonal principal de la matriz. La matriz de identidad tiene\(1\)'s a lo largo de su diagonal principal y\(0\) está en todas partes. A continuación se dan algunos ejemplos de la matriz\(I_{k}\) mencionada en el Teorema 8.5. Se anima al lector a ver cómo coinciden con la definición de la matriz de identidad que allí se presenta.

\[\begin{array}{ccccc} [1] & \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right] & \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] & \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right] \\ I_1 & I_2 & I_3 & I_4 \\ \end{array}\nonumber\]

La matriz de identidad es un ejemplo de lo que se llama matriz cuadrada ya que tiene el mismo número de filas que columnas. Obsérvese que para verificar que la matriz de identidad actúa como una identidad multiplicativa, se debe tener cierto cuidado dependiendo del orden de la multiplicación. Por ejemplo, tome la matriz\(A\) de la\(2 \times 3\) matriz anterior

\[A = \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right]\nonumber\]

Para que se defina el producto\(I_{k}A\),\(k = 2\); de igual manera,\(AI_{k}\) para que se defina,\(k = 3\). Se lo dejamos al lector para mostrar\(I_{2}A = A\) y\(AI_{3} = A\). En otras palabras,

\[\begin{array}{rcl} \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right] \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right] & = & \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right] \\ \end{array}\nonumber\]

y\[\begin{array}{rcl} \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right]\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] & = & \left[\begin{array}{rrr} 2 & \hphantom{-}0 & -1 \\ -10 & 3 & 5 \\ \end{array} \right] \\ \end{array}\nonumber\]

Si bien las pruebas de las propiedades en el Teorema 8.5 son de naturaleza computacional, la notación se involucra bastante rápidamente, por lo que se dejan a un curso en Álgebra Lineal. El siguiente ejemplo proporciona cierta práctica con la multiplicación matricial y sus propiedades. Como es habitual, hay que aprender algunas lecciones valiosas.

Ejemplo 8.3.2

1. Encuentra\(AB\) para\(A = \left[ \begin{array}{rrr} -23 & -1 & 17 \\ 46 & 2 & -34 \\ \end{array} \right]\) y\(B = \left[ \begin{array}{rr} -3 & 2 \\ 1 & 5 \\ -4 & 3 \\ \end{array} \right]\)
2. Buscar\(C^2 -5C + 10I_{2}\) para\(C = \left[ \begin{array}{rr} 1 & -2 \\ 3 & 4 \\ \end{array} \right]\)
3. Supongamos que\(M\) es una\(4 \times 4\) matriz. Usa el Teorema 8.5 para expandir\(\left(M - 2I_{4}\right)\left(M + 3I_{4}\right)\).

Solución.

1. Tenemos\(AB = \left[ \begin{array}{rrr} -23 & -1 & 17 \\ 46 & 2 & -34 \end{array} \right] \left[ \begin{array}{rr} -3 & 2 \\ 1 & 5 \\ -4 & 3 \end{array} \right] = \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \end{array} \right]\)
2. Así como\(x^2\) significa\(x\) tiempos en sí,\(C^2\) denota los\(C\) tiempos de la matriz misma. Obtenemos

   \[\begin{array}{rcl} C^2 -5C + 10I_2 & = & \left[ \begin{array}{rr} 1 & -2 \\ 3 & 4 \\ \end{array} \right]^2 - 5 \left[ \begin{array}{rr} 1 & -2 \\ 3 & 4 \\ \end{array} \right] + 10 \left[ \begin{array}{rr} 1 & 0 \\ 0 & 1 \\ \end{array} \right] \\ & = & \left[ \begin{array}{rr} 1 & -2 \\ 3 & 4 \\ \end{array} \right]\left[ \begin{array}{rr} 1 & -2 \\ 3 & 4 \\ \end{array} \right] + \left[ \begin{array}{rr} -5 & 10 \\ -15 & -20 \\ \end{array} \right] + \left[ \begin{array}{rr} 10 & 0 \\ 0 & 10 \\ \end{array} \right] \\ & = & \left[ \begin{array}{rr} -5 & -10 \\ 15 & 10 \\ \end{array} \right] + \left[ \begin{array}{rr} 5 & 10 \\ -15 & -10 \\ \end{array} \right] \\ & = & \left[ \begin{array}{rr} 0 & 0 \\ 0 & 0 \\ \end{array} \right] \\ \end{array}\nonumber\]

3. Nos expandimos\(\left(M - 2I_{4}\right)\left(M + 3I_{4}\right)\) con el mismo celo pedante que mostramos en el Ejemplo 8.3.1. Se alienta al lector a determinar qué propiedad de la aritmética matricial se utiliza a medida que avanzamos de un paso a otro.

   \[\begin{array}{rcl} \left(M - 2I_4\right)\left(M + 3I_4\right) & = & \left(M - 2I_4\right) M + \left(M - 2I_4\right)\left( 3I_4\right) \\ & = & MM - \left(2I_4\right)M + M\left( 3I_4\right) - \left( 2I_4\right)\left( 3I_4\right) \\ & = & M^2 -2 \left(I_4M\right) +3\left( M I_4\right) - 2\left( I_4\left( 3I_4\right)\right) \\ & = & M^2 - 2M + 3M - 2\left(3\left( I_4I_4\right)\right) \\ & = & M^2 +M - 6I_4 \\ \end{array}\nonumber\]

1. El Ejemplo 8.3.2 ilustra algunas características interesantes de la multiplicación matricial. Primero tenga en cuenta que en la parte 1,\(A\) ni tampoco\(B\) es la matriz cero, sin embargo el producto\(AB\) es la matriz cero. De ahí que la propiedad de producto cero disfrutada por los números reales y la multiplicación escalar no se mantiene para la multiplicación matricial. Las partes 2 y 3 nos introducen en polinomios que involucran matrices. Se anima al lector a dar un paso atrás y comparar nuestra expansión del producto matriz\(\left(M - 2I_{4}\right)\left(M + 3I_{4}\right)\) en la parte 3 con el producto\((x-2)(x+3)\) del álgebra de números reales. Los ejercicios exploran más a fondo este tipo de paralelos.

Como mencionamos anteriormente, un punto\(P(x,y)\) en el\(xy\) plano -puede representarse como una matriz de\(2 \times 1\) posición. Ahora mostramos que la multiplicación matricial puede ser utilizada para rotar estos puntos, y por lo tanto gráficas de ecuaciones.

Ejemplo 8.3.3

Vamos\(R = \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\[4pt] \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{array} \right]\).

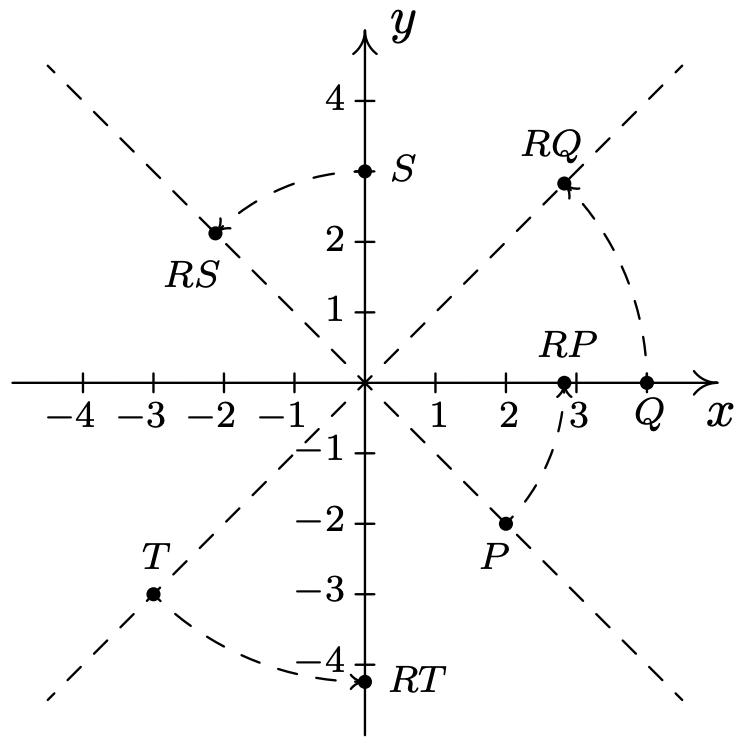
1. Trazar\(P(2,-2)\)\(Q(4,0)\),\(S(0,3)\),, y\(T(-3,-3)\) en el plano así como los puntos\(RP\),\(RQ\),\(RS\), y\(RT\). Trazar las líneas\(y=x\) y\(y=-x\) como guías. ¿Qué\(R\) parece estar haciendo a estos puntos?
2. Si un punto\(P\) está en la hipérbola\(x^2-y^2=4\), mostrar que el punto\(RP\) está en la curva\(y = \frac{2}{x}\).

Solución

Para\(P(2,-2)\), la matriz de posición es\(P = \left[ \begin{array}{r} 2 \\ -2 \\ \end{array} \right]\), y

\[\begin{array}{rcl} RP & = & \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\[4pt] \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ \end{array} \right]\left[ \begin{array}{r} 2 \\[4pt] -2 \\ \end{array} \right] \\ & = & \left[ \begin{array}{r} 2\sqrt{2} \\ 0 \\ \end{array} \right] \\ \end{array}\nonumber\]

Tenemos que\(R\) lleva\((2,-2)\) a\((2 \sqrt{2}, 0)\). De igual manera, encontramos que\((4,0)\) se mueve a\((2\sqrt{2}, 2\sqrt{2})\),\((0,3)\) se mueve a\(\left(-\frac{3 \sqrt{2}}{2}, \frac{3 \sqrt{2}}{2} \right)\), y\((-3,-3)\) se mueve a\((0,-3\sqrt{2})\). Trazando estos en el plano de coordenadas junto con las líneas\(y=x\) y\(y=-x\), vemos que la matriz\(R\) está rotando estos puntos en sentido antihorario por\(45^{\circ}\).

Para un punto genérico\(P(x,y)\) sobre la hipérbola\(x^2-y^2=4\), tenemos

\[\begin{array}{rcl} RP & = & \left[ \begin{array}{rr} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\[4pt] \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ \end{array} \right]\left[ \begin{array}{r} x \\[4pt] y \\ \end{array} \right] \\ & = & \left[ \begin{array}{r} \frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y \\[4pt] \frac{\sqrt{2}}{2} x + \frac{\sqrt{2}}{2} y \\ \end{array} \right] \\ \end{array}\nonumber\]

lo que significa\(R\) lleva\((x,y)\) a\(\left(\frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y, \frac{\sqrt{2}}{2} x + \frac{\sqrt{2}}{2} y\right)\). Para demostrar que este punto está en la curva\(y = \frac{2}{x}\), reemplazamos\(x\) con\(\frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y\) y\(y\) con\(\frac{\sqrt{2}}{2} x + \frac{\sqrt{2}}{2} y\) y simplificamos.

\[\begin{array}{rcl} y & = & \frac{2}{x} \\ \frac{\sqrt{2}}{2} x + \frac{\sqrt{2}}{2} y & \stackrel{?}{=} & \frac{2}{\frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y} \\[10pt] \left(\frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y \right) \left(\frac{\sqrt{2}}{2} x + \frac{\sqrt{2}}{2} y \right)& \stackrel{?}{=} & \left(\dfrac{2}{\frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y}\right) \left( \frac{\sqrt{2}}{2} x - \frac{\sqrt{2}}{2} y \right)\\ \left(\frac{\sqrt{2}}{2} x \right)^2 - \left( \frac{\sqrt{2}}{2} y\right)^2 & \stackrel{?}{=} & 2 \\ \frac{x^2}{2} - \frac{y^2}{2} & \stackrel{?}{=} & 2 \\ x^2 - y^2 & \stackrel{\checkmark }{=}& 4 \\ \end{array}\nonumber\]

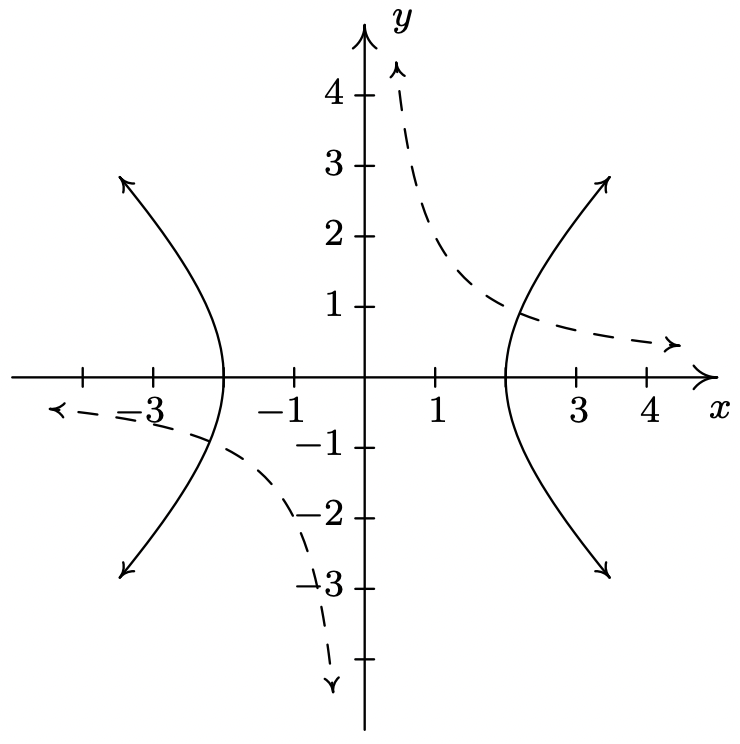
Ya que\((x,y)\) está en la hipérbola\(x^2 - y^2 = 4\), sabemos que esta última ecuación es cierta. Dado que todos nuestros pasos son reversibles, esta última ecuación es equivalente a nuestra ecuación original, que establece que el punto está, en efecto, en la gráfica de\(y = \frac{2}{x}\). Esto significa que la gráfica de\(y=\frac{2}{x}\) es una hipérbola, y no es otra que la hipérbola\(x^2-y^2=4\) girada en sentido antihorario por\(45^{\circ}\). ⁹ A continuación tenemos la gráfica de\(x^2-y^2=4\) (línea continua) y\(y = \frac{2}{x}\) (línea discontinua) para comparación.

Cuando iniciamos esta sección, mencionamos que consideraríamos temporalmente las matrices como sus propias entidades, pero que el álgebra desarrollada aquí en última instancia nos permitiría resolver sistemas de ecuaciones lineales. Para ello, considere el sistema

\[\left\{ \begin{array}{rcl} 3x - y + z & = & 8 \\ x + 2y - z & = & 4 \\ 2x+ 3y - 4z & = & 10 \\ \end{array} \right.\nonumber\]

En la Sección 8.2, codificamos este sistema en la matriz aumentada

\[\left[ \begin{array}{rrr|r} 3 & -1 & 1 & 8 \\ 1 & 2 & -1 & 4 \\ 2 & 3 & -4 & 10 \\ \end{array} \right]\nonumber\]

Recordemos que las entradas a la izquierda de la línea vertical provienen de los coeficientes de las variables en el sistema, mientras que las de la derecha comprenden las constantes asociadas. Por esa razón, podemos formar la matriz de coeficientes\(A\), la matriz de incógnitas\(X\) y la matriz constante\(B\) como se muestra a continuación

\[\begin{array}{ccc} A = \left[ \begin{array}{rrr} 3 & -1 & 1 \\ 1 & 2 & -1 \\ 2 & 3 & -4 \\ \end{array} \right] & X = \left[ \begin{array}{r} x \\ y \\ z \\ \end{array} \right] & B = \left[ \begin{array}{r} 8 \\ 4 \\ 10 \\ \end{array} \right] \end{array}\nonumber\]

Consideramos ahora la ecuación matricial\(AX = B\).

\[\begin{array}{rcl} AX & = & B \\ \left[ \begin{array}{rrr} 3 & -1 & 1 \\ 1 & 2 & -1 \\ 2 & 3 & -4 \\ \end{array} \right] \left[ \begin{array}{r} x \\ y \\ z \\ \end{array} \right] & = & \left[ \begin{array}{r} 8 \\ 4 \\ 10 \\ \end{array} \right] \\ \left[ \begin{array}{rrr} 3x -y +z \\ x + 2y -z \\ 2x + 3y -4 z \\ \end{array} \right] & = & \left[ \begin{array}{r} 8 \\ 4 \\ 10 \\ \end{array} \right] \\ \end{array}\nonumber\]

Vemos que encontrar una solución\((x,y,z)\) al sistema original corresponde a encontrar una solución\(X\) para la ecuación matricial\(AX = B\). Si pensamos en resolver la ecuación del número real\(ax = b\), simplemente “dividiríamos” ambos lados por\(a\). ¿Es posible 'dividir' ambos lados de la ecuación matricial\(AX = B\) por la matriz\(A\)? Este es el tema central de la Sección 8.4.

8.3.1. Ejercicios

Para cada par de matrices\(A\) y\(B\) en Ejercicios 1 - 7, encuentre lo siguiente, si se define

• \(3A\)
• \(-B\)
• \(A^2\)
• \(A-2B\)
• \(AB\)
• \(BA\)

1. \(A = \left[ \begin{array}{rr} 2 & -3 \\ 1 & 4 \end{array} \right]\),\(B=\left[ \begin{array}{rr} 5 & -2 \\ 4 & 8 \end{array} \right]\)
2. \(A = \left[ \begin{array}{rr} -1 & 5 \\ -3 & 6 \end{array} \right]\),\(B=\left[ \begin{array}{rr} 2 & 10 \\ -7 & 1 \end{array} \right]\)
3. \(A = \left[ \begin{array}{rr} -1 & 3 \\ 5 & 2 \end{array} \right]\),\(B=\left[ \begin{array}{rrr} 7 & 0 & 8 \\ -3 & 1 & 4 \end{array} \right]\)
4. \(A = \left[ \begin{array}{rr} 2 & 4 \\ 6 & 8 \end{array} \right]\),\(B=\left[ \begin{array}{rrr} -1 & 3 & -5 \\ 7 & -9 & 11 \end{array} \right]\)
5. \(A = \left[ \begin{array}{r} 7 \\ 8 \\ 9 \end{array} \right]\),\(B=\left[ \begin{array}{rrr} 1 & 2 & 3 \end{array} \right]\)
6. \(A = \left[ \begin{array}{rr} 1 & -2 \\ -3 & 4 \\ 5 & -6 \end{array} \right]\),\(B=\left[ \begin{array}{rrr} -5 & 1 & 8 \end{array} \right]\)
7. \(A = \left[ \begin{array}{rrr} 2 & -3 & 5 \\ 3 & 1 &-2 \\ -7 & 1 & -1 \end{array} \right]\),\(B= \left[ \begin{array}{rrr} 1 & 2 & 1 \\ 17 & 33 & 19 \\ 10 & 19 & 11 \end{array} \right]\)

En los Ejercicios 8 - 21, utilice las matrices\[A = \left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right] \;\;\; B = \left[ \begin{array}{rr} 0 & -3 \\ -5 & 2 \end{array} \right] \;\;\; C = \left[ \begin{array}{rrr} 10 & -\frac{11}{2} & 0 \\ \frac{3}{5} & 5 & 9 \end{array} \right]\nonumber\]\[D = \left[ \begin{array}{rr} 7 & -13 \\ -\frac{4}{3} & 0 \\ 6 & 8 \end{array} \right] \;\;\; E = \left[ \begin{array}{rrr} 1 & \hphantom{-}2 & 3 \\ 0 & 4 & -9 \\ 0 & 0 & -5 \end{array} \right]\nonumber\] para computar lo siguiente o indicar que la operación indicada es indefinida.

8. \(7B - 4A\)
9. \(AB\)
10. \(BA\)
11. \(E + D\)
12. \(ED\)
13. \(CD + 2I_{2}A\)
14. \(A - 4I_{2}\)
15. \(A^2 - B^2\)
16. \((A+B)(A-B)\)
17. \(A^2-5A-2I_{2}\)
18. \(E^2 + 5E-36I_{3}\)
19. \(EDC\)
20. \(CDE\)
21. \(ABCEDI_{2}\)
22. Let\(A = \left[ \begin{array}{rrr} a & b & c \\ d & e & f \end{array} \right] \;\;\; E_{1} = \left[ \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \right] \;\;\; E_{2} = \left[ \begin{array}{rr} 5 & 0 \\ 0 & 1 \end{array} \right] \;\;\; E_{3} = \left[ \begin{array}{rr} 1 & -2 \\ 0 & 1 \end{array} \right]\)

    Computar\(E_{1}A\),\(\; E_{2}A\) y\(E_{3}A\). ¿Qué efecto tuvo cada una de las\(E_{i}\) matrices en las filas de\(A\)? Crear\(E_{4}\) para que su efecto sobre\(A\) sea multiplicar la fila inferior por\(-6\). ¿Cómo extenderías esta idea a matrices con más de dos filas?

---

Referencia

¹ Recordemos que significa que\(A\) tiene\(m\) filas y\(n\) columnas.

² Los críticos bien pueden preguntar: ¿Por qué no dejarlo así? ¿Por qué la necesidad de toda la notación en la Definición 8.6? Es el intento de los autores de exponerte al maravilloso mundo de la precisión matemática.

³ Un detalle técnico que lamentablemente se pierde en la mayoría de los lectores.

⁴ La Propiedad Distributiva, en particular.

⁵ Ver Sección 1.7.

⁶ Consulte este artículo sobre el Producto Hadamard.

⁷ Se anima al lector a pensar esto detenidamente.

⁸ Y puede que ni siquiera tengan las mismas dimensiones. Por ejemplo, si\(A\) es una matriz de 2×3 y B es una matriz de 3×2, entonces\(AB\) se define y es una matriz de 2×2 mientras que BA también se define... ¡pero es una matriz de 3×3!

⁹ Consulte la Sección 7.5 para más detalles.