2.1: Funciones lineales
- Page ID
- 116749
A medida que te subes a un taxi en Las Vegas, el medidor leerá inmediatamente $3.50; esta es la carga de “caída” que se realiza cuando se activa el taxímetro. Después de esa tarifa inicial, el taxímetro sumará $2.76 por cada milla que conduzca el taxi (Nevada Taxicab Authority, recuperado el 8 de mayo de 2017. También se cobra una tarifa de espera cuando el taxi está esperando en semáforos rojos, pero lo ignoraremos en esta discusión. Este capítulo es parte de Precálculo: Una investigación de funciones © Lippman & Rasmussen 2017. Este material está bajo una licencia Creative Commons CC-BY-SA.). En este escenario, la tarifa total del taxi depende del número de millas recorridas en el taxi, y podemos preguntar si es posible modelar este tipo de escenarios con una función. Usando variables descriptivas, elegimos\(m\) para millas y\(C\) para Costo en dólares en función de millas:\(C(m)\).
Sabemos con certeza que\(C(0)=3.50\), ya que el cargo por caída de $3.50 se evalúa independientemente de cuántas millas se conduzcan. Desde $2.67 se agrega por cada milla conducida, entonces
\[C(1)=3.50+2.67=6.17\nonumber \]
Si luego manejamos una segunda milla, se agregarían otros $2.67 al costo:
\[C(2)=3.50+2.67+2.67=3.50+2.67(2)=8.84\nonumber \]
Si manejáramos una tercera milla, se agregarían otros $2.67 al costo:
\[C(3)=3.50+2.67+2.67+2.67=3.50+2.67(3)=11.51\nonumber \]
De esto podríamos observar el patrón, y concluir que si se\(m\) recorren millas,
\(C(m)=3.50+2.67m\)porque comenzamos con una tarifa de caída de $3.50 y luego por cada aumento de milla agregamos $2.67.
Es bueno verificar que las unidades tengan sentido en esta ecuación. El cargo por caída de $3.50 se mide en dólares; el cargo de $2.67 se mide en dólares por milla.
\[C(m)=3.50\text{ dollars}+\left(2.67\dfrac{\text{dollars}}{\text{mile}} \right)\left(m\; \text{ miles}\right)\nonumber \]
Cuando los dólares por milla se multiplican por un número de millas, el resultado es un número de dólares, igualando las unidades en el 3.50, y igualando las unidades deseadas para la función C.
Observe que esta ecuación\(C(m)=3.50+2.67m\) consistió en dos cantidades. El primero es el cargo fijo de $3.50 que no cambia con base en el valor de la entrada. El segundo es el valor de $2.67 dólares por milla, que es una tasa de cambio. En la ecuación, esta tasa de cambio se multiplica por el valor de entrada.
Al observar este mismo problema en formato de tabla también podemos ver los cambios de costos en $2.67 por cada aumento de 1 milla.
| \(m\) | 0 | 1 | 2 | 3 |
| \(C(m)\) | 3.50 | 6.17 | 8.84 | 11.51 |
Aquí es importante señalar que en esta ecuación, la tasa de cambio es constante; en cualquier intervalo, la tasa de cambio es la misma.
Graficando esta ecuación,\(C(m)=3.50+2.67m\) vemos que la forma es una línea, que es como estas funciones obtienen su nombre: funciones lineales.
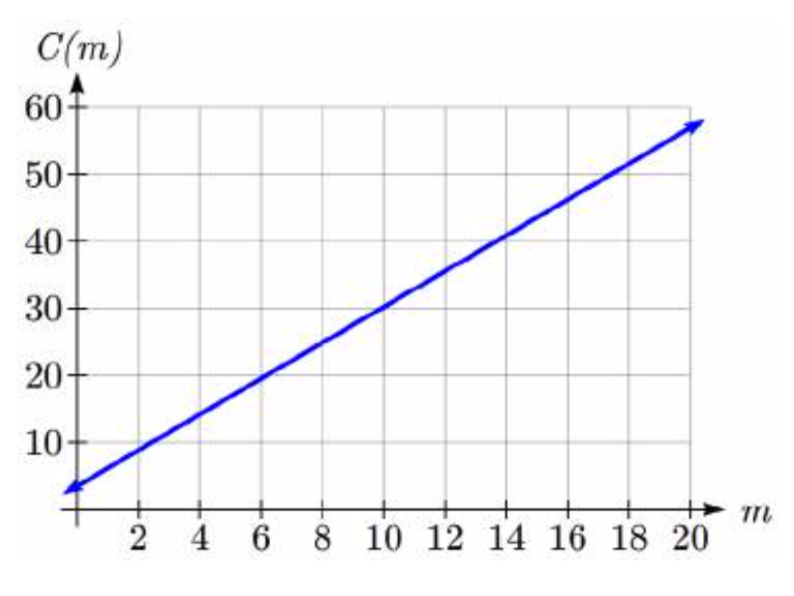
Cuando el número de millas es cero el costo es de $3.50, dando el punto (0, 3.50) en la gráfica. Esta es la vertical o\(C(m)\) intercepción. El gráfico está aumentando en línea recta de izquierda a derecha porque por cada milla el costo sube 2.67 dólares; esta tasa sigue siendo consistente.
En este ejemplo, has visto el costo del taxi modelado en palabras, una ecuación, una tabla y en forma gráfica. Siempre que sea posible, asegúrese de vincular estas cuatro representaciones para desarrollar continuamente sus habilidades. Es importante tener en cuenta que no siempre podrás encontrar las 4 representaciones para un problema y así poder trabajar con las 4 formas es muy importante.
Definición: Función lineal
Una función lineal es una función cuya gráfica produce una línea. Las funciones lineales siempre se pueden escribir en la forma
\(f(x)=b+mx\)o\(f(x)=mx+b\); son equivalentes
donde
- \(b\)es el valor inicial o inicial de la función (cuando se introduce, x = 0), y
- \(m\)es la tasa constante de cambio de la función
A muchas personas les gusta escribir funciones lineales en la forma\(f(x)=b+mx\) porque corresponde a la forma en que tendemos a hablar: “La salida comienza en\(b\) y aumenta a un ritmo de”\(m\).
Solo por esta razón usaremos el\(f(x)=b+mx\) formulario para muchos de los ejemplos, pero recuerda que son equivalentes y se pueden escribir correctamente en ambos sentidos.
Definición: pendiente y aumento/decreciente
\(m\)es la tasa constante de cambio de la función (también llamada pendiente). Pendiente La pendiente determina si la función es una función creciente o una función decreciente.
\(f(x)=b+mx\)es una función creciente si\(m>0\)
\(f(x)=b+mx\)es una función decreciente si\(m<0\)
Si\(m=0\), la tasa de cambio cero, y la función\(f(x)=b+0x=b\) es solo una línea horizontal que pasa por el punto (0,\(b\)), ni aumentando ni disminuyendo.
Ejemplo\(\PageIndex{1}\)
Actualmente Marcus posee 200 canciones en su colección de iTunes. Cada mes, agrega 15 canciones nuevas. Escribir una fórmula para el número de canciones,\(N\), en su colección de iTunes en función del número de meses,\(m\). ¿Cuántas canciones tendrá en un año?
Solución
El valor inicial para esta función es de 200, ya que actualmente posee 200 canciones, entonces\(N(0)=200\). El número de canciones aumenta en 15 canciones al mes, por lo que la tasa de cambio es de 15 canciones al mes. Con esta información, podemos escribir la fórmula:
\[N(m)=200+15m\nonumber \]
\(N(m)\)es una función lineal creciente. Con esta fórmula podemos predecir cuántas canciones tendrá en 1 año (12 meses):
\[N(12)=200+15(12)=200+180=380\nonumber \]Marcus tendrá 380 canciones en 12 meses.
Ejercicio\(\PageIndex{1}\)
Si ganas 30,000 dólares anuales y gastas $29,000 al año escribe una ecuación por la cantidad de dinero que ahorras después de y años, si empiezas sin nada.
“Lo más importante, ¡gasta menos de lo que ganas! (http://www.thesimpledollar.com/2009/...than-you-earn/)”
- Contestar
-
\(S(y)=30,000y - 29,000y = 1000y\)Se ahorran $1000 cada año.
Definición: Cálculo de la tasa de cambio
Dados dos valores para la entrada\(x_{1} {\rm \; and\; }x_{2}\),, y dos valores correspondientes para la salida\(y_{1} {\rm \; and\; }y_{2}\),, o un conjunto de puntos\((x_{2} {\rm ,\; \; }y_{2} )\),\((x_{1} {\rm ,\; \; }y_{1} )\) y, si deseamos encontrar una función lineal que contenga ambos puntos podemos calcular la tasa de cambio, m:
\[m=\dfrac{\rm change\; in\; output}{\rm change\; in\; input} =\dfrac{\Delta y}{\Delta x} =\dfrac{y_{2} -y_{1} }{x_{2} -x_{1} }\]
La tasa de cambio de una función lineal también se llama la pendiente de la línea.
Nota en notación de funciones\(y_{2} =f(x_{2} )\),\(y_{1} =f(x_{1} )\) y, así podríamos escribir equivalentemente
\[m=\dfrac{f\left(x_{2} \right)-f\left(x_{1} \right)}{x_{2} -x_{1} }\]
Ejemplo\(\PageIndex{2}\)
La población de una ciudad aumentó de 23,400 a 27,800 entre 2002 y 2006. Encuentra la tasa de cambio de la población durante este lapso de tiempo.
Solución
La tasa de cambio relacionará el cambio en la población con el cambio en el tiempo. La población aumentó en\(27800-23400=4400\) personas durante el intervalo de tiempo de 4 años. Para encontrar la tasa de cambio, el número de personas por año la población cambió por:
\[\dfrac{4400\text{ people}}{4\text{ years}} =1100\dfrac{\text{people}}{\text{year}}= 1100\text{ people per year}\nonumber\]
Observe que sabíamos que la población iba en aumento, por lo que esperaríamos\(m\) que nuestro valor fuera positivo. Esta es una forma rápida de verificar si tu valor es razonable.
Ejemplo\(\PageIndex{3}\)
La presión,\(P\), en libras por pulgada cuadrada (PSI) sobre un buceador depende de su profundidad por debajo de la superficie del agua\(d\),, en pies, siguiendo la ecuación\(P(d)=14.696+0.434d\). Interpretar los componentes de esta función.
Solución
La tasa de cambio, o pendiente, 0.434 tendría unidades\(\dfrac{\text{output}}{\text{input}} = \dfrac{\text{pressure}}{\text{depth}} = \dfrac{\text{PSI}}{\text{ft}}\). Esto nos dice que la presión sobre el buceador aumenta en 0.434 PSI por cada pie aumenta su profundidad.
El valor inicial, 14.696, tendrá las mismas unidades que la salida, por lo que esto nos dice que a una profundidad de 0 pies, la presión sobre el buceador será de 14.696 PSI.
Ejemplo\(\PageIndex{4}\)
Si\(f(x)\) es una función lineal,\(f(3)=-2\), y\(f(8)=1\), encontrar la tasa de cambio.
Solución
\(f(3)=-2\)nos dice que la entrada 3 corresponde con la salida -2, y nos\(f(8)=1\) dice que la entrada 8 corresponde con la salida 1. Para encontrar la tasa de cambio, dividimos el cambio en la salida por el cambio en la entrada:
\[m=\dfrac{\text{change in output}}{\text{change in input}} =\dfrac{1-(-2)}{8-3} =\dfrac{3}{5}\nonumber\]Si lo desea también podríamos escribir esto como\(m = 0.6\)
Tenga en cuenta que no es importante qué par de valores viene primero en las restaciones siempre y cuando el primer valor de salida utilizado corresponda con el primer valor de entrada utilizado.
Ejercicio\(\PageIndex{2}\)
Dados los dos puntos (2, 3) y (0, 4), encuentra la tasa de cambio. ¿Esta función está aumentando o disminuyendo?
- Contestar
-
\(m=\dfrac{4-3}{0-2} =\dfrac{1}{-2} =-\dfrac{1}{2}\); Disminuyendo porque\(m < 0\)
Ahora podemos encontrar la tasa de cambio dado dos pares entrada-salida, y podemos escribir una ecuación para una función lineal una vez que tenemos la tasa de cambio y el valor inicial. Si tenemos dos pares entrada-salida y no incluyen el valor inicial de la función, entonces tendremos que resolverlo.
Ejemplo\(\PageIndex{5}\)
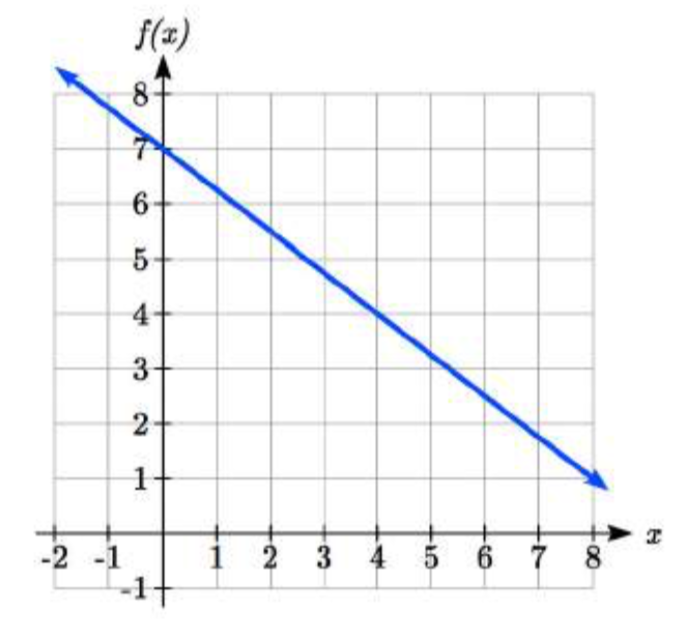
Escribe una ecuación para la función lineal graficada a la derecha.
Solución
Al mirar la gráfica, podríamos notar que pasa por los puntos (0, 7) y (4, 4). Desde el primer valor, sabemos que el valor inicial de la función es\(b = 7\), por lo que en este caso solo necesitaremos calcular la tasa de cambio:
\[m=\dfrac{4-7}{4-0} =\dfrac{-3}{4}\nonumber \]
Esto nos permite escribir la ecuación:
\[f(x)=7-\dfrac{3}{4} x\nonumber \]
Ejemplo\(\PageIndex{6}\)
Si\(f(x)\) es una función lineal,\(f(3)=-2\), y\(f(8)=1\), encontrar una ecuación para la función.
Solución
En el ejemplo 3, calculamos la tasa de cambio a ser\(m=\dfrac{3}{5}\). En este caso, desconocemos el valor inicial\(f(0)\), por lo que tendremos que resolverlo. Usando la tasa de cambio, sabemos que la ecuación tendrá la forma\(f(x)=b+\dfrac{3}{5} x\). Ya que conocemos el valor de la función cuando\(x = 3\), podemos evaluar la función en 3.
\[f(3)=b+\dfrac{3}{5} (3)\nonumber \]Como sabemos eso\(f(3)=-2\), podemos sustituir por el lado izquierdo
\[-2=b+\dfrac{3}{5} (3)\nonumber \]Esto nos deja con una ecuación que podemos resolver para el valor inicial
\[b=-2-\dfrac{9}{5} =\dfrac{-19}{5}\nonumber \]
Combinando esto con el valor de la tasa de cambio, ahora podemos escribir una fórmula para esta función:
\[f(x)=\dfrac{-19}{5} +\dfrac{3}{5} x\nonumber \]
Ejemplo\(\PageIndex{7}\)
Al trabajar como vendedor de seguros, Ilya gana un salario base y una comisión por cada nueva póliza, por lo que el ingreso semanal de Ilya\(I\),, depende del número de pólizas nuevas\(n\),, vende durante la semana. La semana pasada vendió 3 nuevas pólizas, y ganó 760 dólares por semana. La semana anterior, vendió 5 nuevas pólizas, y ganó $920. Encontrar una ecuación para\(I(n)\), e interpretar el significado de los componentes de la ecuación.
Solución
La información dada nos da dos pares entrada-salida: (3,760) y (5,920). Comenzamos por encontrar la tasa de cambio.
\[m=\dfrac{920-760}{5-3} =\dfrac{160}{2} =80\nonumber \]
Hacer un seguimiento de las unidades puede ayudarnos a interpretar esta cantidad. Los ingresos aumentaron 160 dólares cuando el número de pólizas aumentó en 2, por lo que la tasa de cambio es de 80 dólares por póliza; Ilya gana una comisión de 80 dólares por cada póliza vendida durante la semana.
Entonces podemos resolver para el valor inicial
\[I(n)=b+80n\nonumber\]entonces cuando\(n = 3\),\(I(3)=760\), dando
\[760=b+80(3)\nonumber \]esto nos permite resolver\(b\)
\[b=760-80(3)=520\nonumber \]
Este valor es el valor inicial de la función. Este es el ingreso de Ilya cuando\(n = 0\), lo que significa que no se venden nuevas pólizas. Podemos interpretar esto como el salario base de Ilya para la semana, que no depende del número de pólizas vendidas.
Escribiendo la ecuación final:
\[I(n)=520+80n\nonumber \]
Nuestra interpretación final es: el salario base de Ilya es de 520 dólares semanales y gana una comisión adicional de 80 dólares por cada póliza vendida cada semana.
flashback
Mirando el Ejemplo 7:
Determinar las variables independientes y dependientes.
¿Qué es un dominio y un rango razonables?
¿Esta función es uno a uno?
- Contestar
-
\(n\)(número de pólizas vendidas) es la variable independiente
\(I(n)\)(ingreso semanal en función de las pólizas vendidas) es la variable dependiente.
Un dominio razonable es (0, 15)\({}^{*}\)
Un rango razonable es ($540, $1740)\({}^{*}\)
\({}^{*}\)las respuestas pueden variar dado que se establece el razonamiento; 15 es un límite superior arbitrario basado en la venta de 3 pólizas por día en una semana laboral de 5 días y $1740 corresponde con el dominio.
Sí, esta función es uno a uno
Ejercicio\(\PageIndex{3}\)
El saldo en tu cuenta de pagos universitarios\(C\),, es función del número de trimestres,\(q\), asistes. Interpretar la función\(C(a) = 20000 – 4000q\) en palabras. ¿Cuántos cuartos de universidad puedes pagar hasta que esta cuenta esté vacía?
- Contestar
-
Tu cuenta de College comienza con $20,000 en ella y retiras $4,000 cada trimestre (o tu cuenta contiene $20,000 y disminuye en $4000 cada trimestre). Resolver\(C(a) = 0\) da\(a = 5\). Puedes pagar 5 trimestres antes de que el dinero de esta cuenta se vaya.
Ejemplo\(\PageIndex{8}\)
Dada la siguiente tabla escribir una ecuación lineal que representa los valores de la tabla
| \(w\), número de semanas | 0 | 2 | 4 | 6 |
| \(P(w)\), número de ratas | 1000 | 1080 | 1160 | 1240 |
Solución
Podemos ver en la tabla que el valor inicial de ratas es 1000 por lo que en el formato lineal
\[P(w)=b+mw,\: b = 1000\nonumber\]
En lugar de resolver por\(m\), podemos notar de la tabla que la población sube 80 por cada 2 semanas que pasan. Esta tasa es consistente desde la semana 0 hasta la semana 2, 4 y 6. La tasa de cambio es de 80 ratas por 2 semanas. Esto se puede simplificar a 40 ratas por semana y podemos escribir
\[P(w)=b+mw\text{ as }P(w)=1000+40w\nonumber \]
Si no notaste esto desde la tabla aún podrías resolver para la pendiente usando dos puntos cualesquiera de la tabla. Por ejemplo, usando (2, 1080) y (6, 1240),
\[m=\dfrac{1240-1080}{6-2} =\dfrac{160}{4} =40\text{ rats per week}\nonumber\]
Temas Importantes de esta Sección
- Definición de Modelado
- Definición de una función lineal
- Estructura de una función lineal
- Funciones crecientes y decrecientes
- Encontrar la intercepción vertical (0, b)
- Encontrar la pendiente/tasa de cambio, m
- Interpretación de funciones lineales


