2.4.4E: Ajuste de Modelos Lineales a Datos (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 116737

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

sección 2.4 ejercicio

1. A continuación se presentan datos para las puntuaciones del primer y segundo cuestionario para 8 alumnos de una clase. Trace los puntos y luego dibuje una línea que se ajuste a los datos.

Primer Quiz	11	20	24	25	33	42	46	49
Segundo Quiz	10	16	23	28	30	39	40	49

2. Se pidió a ocho estudiantes que estimaran su puntaje en un cuestionario de 10 puntos. Se dan sus puntuaciones estimadas y reales. Trace los puntos y luego dibuje una línea que se ajuste a los datos.

Predijo	5	7	6	8	10	9	10	7
Real	6	6	7	8	9	9	10	6

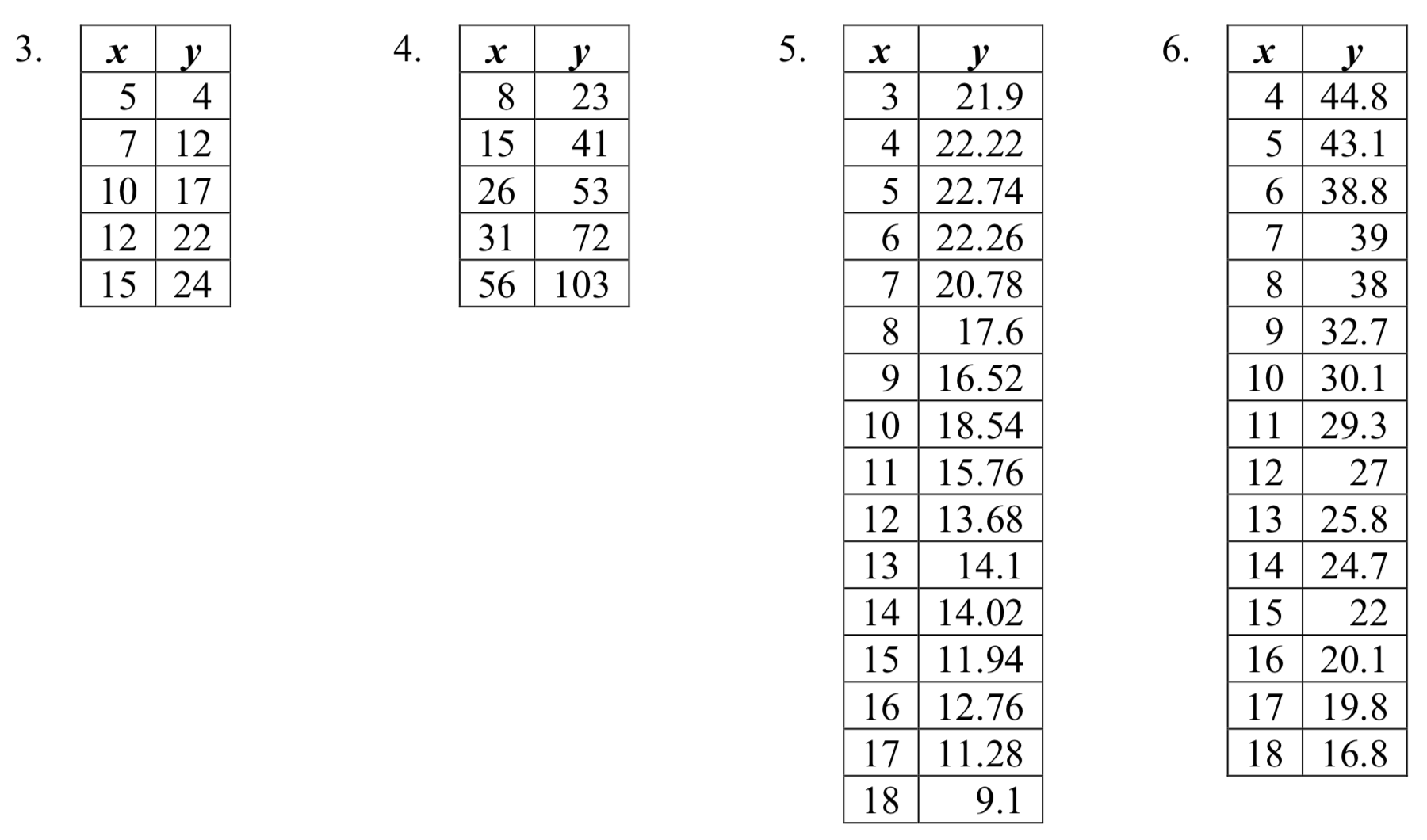
Con base en cada conjunto de datos dados, calcule la línea de regresión usando su calculadora u otra herramienta tecnológica, y determine el coeficiente de correlación.

$2019-06-21 7.17.39.png$

7. Se realizó una regresión para determinar si existe una relación entre las horas de televisión que se ven al día ($x$) y el número de situps que una persona puede hacer ($y$). A continuación se dan los resultados de la regresión. Usa esto para predecir la cantidad de situps que puede hacer una persona que ve 11 horas de televisión.

$y=ax+b$
$a=-1.341$
$b=32.234$
$r^2=0.803$
$r=-0.896$

8. Se realizó una regresión para determinar si existe una relación entre el diámetro de un árbol ($x$, en pulgadas) y la edad del árbol ($y$, en años). A continuación se dan los resultados de la regresión. Use esto para predecir la edad de un árbol con diámetro de 10 pulgadas.

$y=ax+b$
$a=6.301$
$b=-1.044$
$r^2=0.940$
$r=0.970$

Haga coincidir cada diagrama de dispersión que se muestra a continuación con una de las cuatro correlaciones especificadas.

9. $r = 0.95$10. $r = -0.89$11. $r = 0.26$12. $r = -0.39$

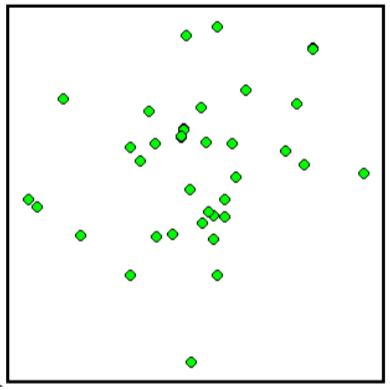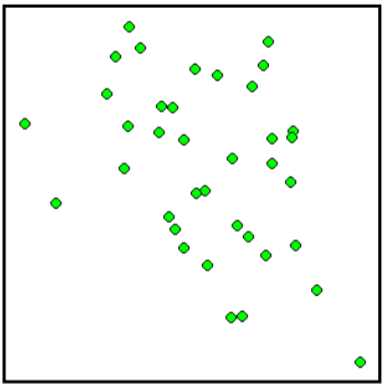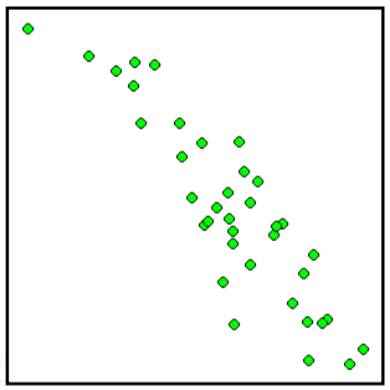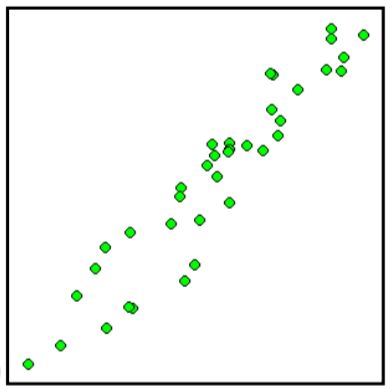
A $2019-06-21 7.21.11.png$ B $2019-06-21 7.21.38.png$ C $2019-06-21 7.22.12.png$ D $2019-06-21 7.22.37.png$

13. El censo de Estados Unidos rastrea el porcentaje de personas de 25 años o más que son egresados universitarios. Esos datos de varios años se dan a continuación. Determinar si la tendencia aparece lineal. Si es así y la tendencia continúa, ¿en qué año el porcentaje superará el 35%?

Año	1990	1992	1994	1996	1998	2000	2002	2004	2006	2008
Porcentaje de egresados	21.3	21.4	22.2	23.6	24.4	25.6	26.7	27.7	28	29.4

14. A continuación se da la importación estadounidense de vino (en hectolitros) durante varios años. Determinar si la tendencia aparece lineal. Si es así y la tendencia continúa, ¿en qué año las importaciones superarán los 12 mil hectolitros?

Año	1992	1994	1996	1998	2000	2002	2004	2006	2008	2009
Importaciones	2665	2688	3565	4129	4584	5655	6549	7950	8487	9462

Contestar

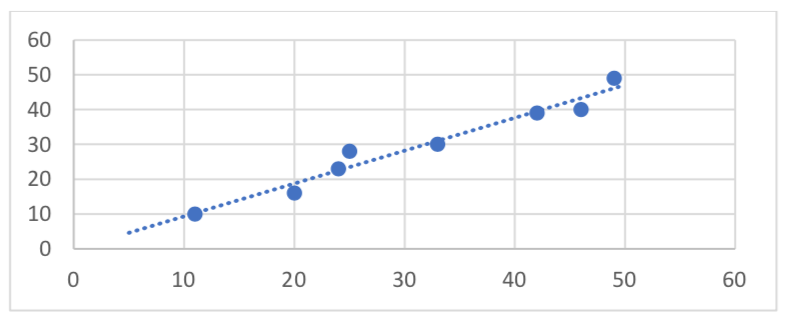
1. $Screen Shot 2019-10-01 a las 8.20.41 PM.png$

3. $y = 1.971x - 3.519$,$r = 0.967$

5. $y = -0.901x + 26.04$,$r = -0.968$

7. $17.483 \approx 17\ situps$

9. D

11. A

13. Sí, la tendencia aparece lineal porque$r = 0.994$ y superará el 35% cerca de finales del año 2019.