Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

2.5: Funciones de valor absoluto

Última actualización

30 oct 2022
Guardar como PDF
- 2.4.4E: Ajuste de Modelos Lineales a Datos (Ejercicios)
- 2.5.5E: Funciones de Valor Absoluto (Ejercicios)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

En lo que va de este capítulo hemos estado estudiando el comportamiento de las funciones lineales. La Función de Valor Absoluto es una función definida por partes compuesta por dos funciones lineales. El nombre, Función de Valor Absoluto, le debería ser familiar a partir de la Sección 1.2. En su forma básica $f(x)=\left|x\right|$ es una de nuestras funciones de kit de herramientas.

Definición: Función de valor absoluto

La función de valor absoluto se puede definir como

$f(x)=\left|x\right|=\left\{\begin{array}{ccc} {x} & {if} & {x\ge 0} \\ {-x} & {if} & {x<0} \end{array}\right.$

La función de valor absoluto se usa comúnmente para determinar la distancia entre dos números en la línea numérica. Dados dos valores a y b, entonces $\left|a-b\right|$ dará la distancia, una cantidad positiva, entre estos valores, independientemente de qué valor sea mayor.

Ejemplo $\PageIndex{1}$

Describir todos los valores $x$ ,, dentro de una distancia de 4 del número 5.

Solución

Queremos que la distancia entre $x$ y 5 sea menor o igual a 4. La distancia se puede representar usando el valor absoluto, dando la expresión

$\left|x-5\right|\le 4\nonumber$

Ejemplo $\PageIndex{2}$

Una encuesta de 2010 reportó que 78% de los estadounidenses cree que las personas homosexuales deberían poder servir en el ejército estadounidense, con un margen de error reportado del 3% (http://www.pollingreport.com/civil.htm, recuperado el 4 de agosto de 2010). El margen de error nos dice qué tan lejos podría estar el valor real del valor de la encuesta (Técnicamente, el margen de error generalmente significa que los topógrafos están 95% seguros de que el valor real cae dentro de este rango). Expresar el conjunto de valores posibles utilizando valores absolutos.

Solución

Dado que queremos que el tamaño de la diferencia entre el porcentaje real $p$ ,, y el porcentaje reportado sea inferior al 3%,

$\left|p-78\right|\le 3\nonumber$

Ejercicio $\PageIndex{1}$

Los alumnos que puntúen dentro de los 20 puntos de 80 pasarán la prueba. Escribe esto como una distancia desde 80 usando la notación de valor absoluto.

Contestar: Usando la variable p, para pasar, $\left|p-80\right|\le 20$

Características Importantes

La característica más significativa del valor absoluto GraphabSolute Value Funcions:Graficar es el punto de esquina donde la gráfica cambia de dirección. Al encontrar la ecuación para una función de valor absoluto transformado, este punto es muy útil para determinar los desplazamientos horizontales y verticales.

Ejemplo $\PageIndex{3}$

Escribe una ecuación para la función graficada.

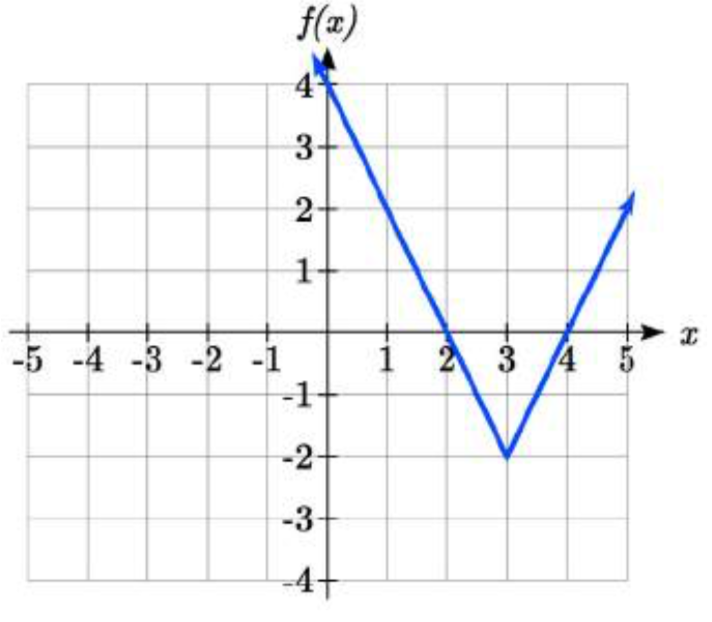
$Una gráfica de valores absolutos en forma de V con punto de esquina en 3 comas negativas 2 y pasando por 1 coma 2 y 4 coma 0$

Solución

La función de valor absoluto básico cambia de dirección en el origen, por lo que esta gráfica se ha desplazado hacia la derecha 3 y hacia abajo 2 desde la función básica del kit de herramientas.

También podríamos notar que la gráfica aparece estirada, ya que las porciones lineales tienen pendientes de 2 y -2. A partir de esta información podríamos escribir la ecuación de dos maneras:

$f(x)=2\left|x-3\right|-2$ , tratando el estiramiento como un estiramiento vertical

$f(x)=\left|2(x-3)\right|-2$ , tratando el estiramiento como una compresión horizontal

Tenga en cuenta que estas ecuaciones son algebraicamente equivalentes — el estiramiento para una función de valor absoluto se puede escribir indistintamente como un estiramiento/compresión vertical u horizontal.

Si no has podido determinar el estiramiento en función de las pendientes de las líneas, puedes resolver para el factor de estiramiento poniendo un par conocido de valores para x y f (x)

$f(x)=a\left|x-3\right|-2\nonumber$ Ahora sustituyendo en el punto (1, 2)

$\begin{array}{l} {2=a\left|1-3\right|-2} \\ {4=2a} \\ {a=2} \end{array}\nonumber$

Ejercicio $\PageIndex{2}$

Dada la descripción de la función de valor absoluto transformado escribir la ecuación. La función de valor absoluto se desplaza horizontalmente a la izquierda 2 unidades, se voltea verticalmente y se desplaza verticalmente hacia arriba 3 unidades.

Contestar: $f(x)=-\left|x+2\right|+3\nonumber$

La gráfica de una función de valor absoluto tendrá una intersección vertical cuando la entrada sea cero. La gráfica puede tener o no intercepciones horizontales, dependiendo de cómo se haya desplazado y reflejado la gráfica. Es posible que la función de valor absoluto tenga cero, una o dos intercepciones horizontales.

Cero intercepciones horizontales Uno Dos Uno Dos

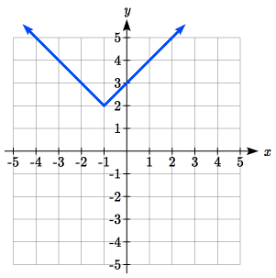
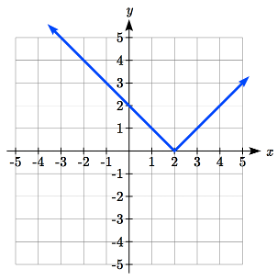
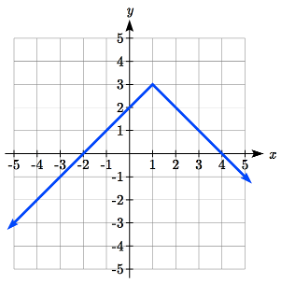
$Un gráfico de valores absolutos en forma de V que se abre hacia arriba con el punto de esquina en negativo 1 coma 2 y pasando por 0 coma 3. No tiene intercepciones horizontales.$ $Un gráfico de valores absolutos en forma de V que se abre hacia arriba con el punto de esquina en 2 coma 0 y pasando por 3 coma 1. Tiene una intercepción horizontal en el punto de la esquina.$ $Un gráfico de valores absolutos en forma de V que se abre hacia abajo con el punto de esquina en 1 coma 3 y dos intercepciones horizontales en negativo 2 coma 0 y 4 coma 0$

Para encontrar las intercepciones horizontales, necesitaremos resolver una ecuación que involucre un valor absoluto.

Observe que la función de valor absoluto no es uno a uno, por lo que normalmente no se discuten las inversas de las funciones de valor absoluto.

Resolver ecuaciones de valor absoluto

Funciones de valor absoluto:Resolver

Para resolver una ecuación como $8=\left|2x-6\right|$ , podemos notar que el valor absoluto será igual a ocho si la cantidad dentro del valor absoluto fuera 8 o -8. Esto lleva a dos ecuaciones diferentes que podemos resolver de forma independiente:

$2x - 6 = 8\text{ or }2x - 6 = -8\nonumber$

$2x = 14\quad 2x = -2\nonumber$

$x = 7\quad x = -1\nonumber$

soluciones a ecuaciones de valor absoluto

Una ecuación de la forma $\left|A\right|=B$ , con $B\ge 0$ , tendrá soluciones cuando

$A=B\text{ or }A=-B\nonumber$

Ejemplo $\PageIndex{4}$

Encuentra las intercepciones horizontales de la gráfica de $f(x)=\left|4x+1\right|-7$

Solución

Las intercepciones horizontales ocurrirán cuando $f(x)=0$ . Resolviendo,

$0=|4x+1|-7\nonumber$ Aislar el valor absoluto en un lado de la ecuación

$7=|4x+1|\nonumber$ Ahora podemos dividir esto en dos ecuaciones separadas:

$7 = 4x + 1\quad -7 = 4x + 1\nonumber$

$6 = 4x\text{ or }-8 = 4x\nonumber$

$x = \dfrac{6}{4} = \dfrac{3}{2}\quad x = \dfrac{-8}{4} = -2\nonumber$

La gráfica tiene dos intercepciones horizontales, a $x=\dfrac{3}{2}$ y $x = -2$

Ejemplo $\PageIndex{5}$

Resolver $1=4\left|x-2\right|+2$

Solución

Aislar el valor absoluto en un lado de la ecuación,

$1=4\left|x-2\right|+2\nonumber$

$-1=4\left|x-2\right|\nonumber$

$-\dfrac{1}{4} =\left|x-2\right|\nonumber$

En este punto, notamos que esta ecuación no tiene soluciones —el valor absoluto siempre devuelve un valor positivo, por lo que es imposible que el valor absoluto sea igual a un valor negativo.

Ejercicio $\PageIndex{3}$

Encuentra las intercepciones horizontales y verticales para la función $f(x)=-\left|x+2\right|+3$

Contestar

$f(0) = 1$ , por lo que la intersección vertical está en (0,1).

$f(x)= 0$ cuando

$-\left|x+2\right|+3=0\nonumber$

$\left|x+2\right|=3\nonumber$

$x+2=3\text{ or }x+2=-3\nonumber$

$x = 1\text{ or }x = -5\nonumber$ por lo que las intercepciones horizontales están en (-5,0) y (1,0)

Resolver desigualdades de valor absoluto

Funciones de valor absoluto:Resolver desigualdades

Cuando las desigualdades de valores absolutos se escriben para describir un conjunto de valores, como la desigualdad que $\left|x-5\right|\le 4$ escribimos anteriormente, a veces es deseable expresar este conjunto de valores sin el valor absoluto, ya sea usando desigualdades, o usando notación de intervalos.

Exploraremos dos enfoques para resolver las desigualdades de valor absoluto:

Uso de la gráfica
Uso de valores de prueba

Ejemplo $\PageIndex{6}$

Resolver $\left|x-5\right|\le 4$

Solución

Con ambos enfoques, necesitaremos saber primero dónde es verdadera la igualdad correspondiente. En este caso, primero encontraremos dónde $\left|x-5\right|=4$ . Hacemos esto porque el valor absoluto es una buena función amigable sin descansos, por lo que la única forma en que los valores de la función pueden pasar de ser menores de 4 a ser mayores que 4 es pasando por donde los valores son iguales a 4. Resolver $\left|x-5\right|=4$ ,

$\begin{array}{l} {x-5=4} \\ {x=9} \end{array}\text{ or } \begin{array}{l} {x-5=-4} \\ {x=1} \end{array}\nonumber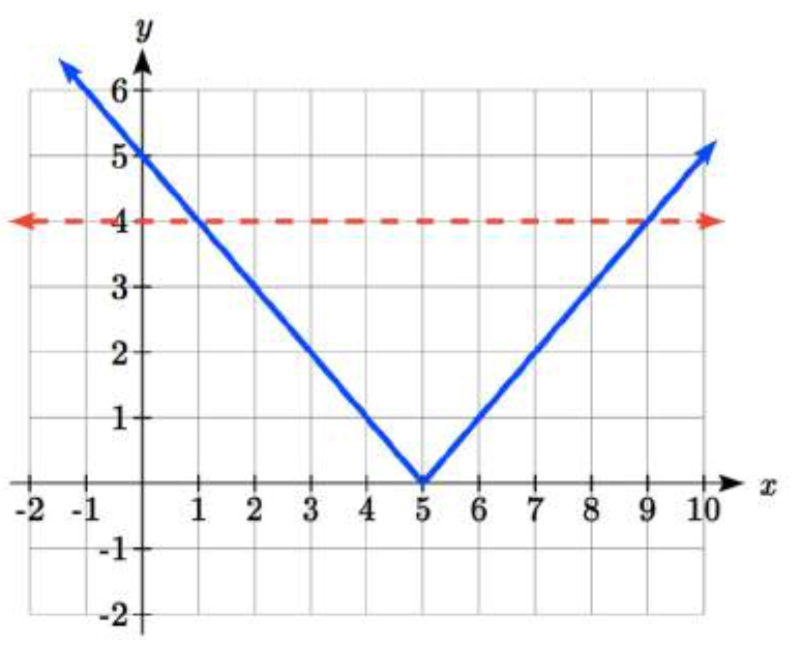$ $Una gráfica de valores absolutos en forma de V con punto de esquina en 5 coma 0 y pasando por 0 coma 5, y una línea discontinua horizontal en y=4. Las gráficas se cruzan en 1 coma 4 y 9 coma 4.$

Para usar una gráfica, podemos bosquejar la función $f(x)=\left|x-5\right|$ . Para ayudarnos a ver dónde están las salidas 4, también se $g(x)=4$ podría esbozar la línea.

En la gráfica, podemos ver que efectivamente los valores de salida del valor absoluto son iguales a 4 at $x = 1$ y $x = 9$ . Con base en la forma de la gráfica, podemos determinar que el valor absoluto es menor o igual a 4 entre estos dos puntos, cuando $1 \le x \le 9$ . En notación de intervalos, este sería el intervalo [1,9].

Como alternativa a la gráfica, después de determinar que el valor absoluto es igual a 4 at $x = 1$ y $x = 9$ , sabemos que la gráfica sólo puede cambiar de ser menor de 4 a mayor de 4 en estos valores. Esto divide la línea de números en tres intervalos: $x < 1$ , $1 < x < 9$ , y $x > 9$ . Para determinar cuándo la función es menor que 4, podríamos escoger un valor en cada intervalo y ver si la salida es menor o mayor que 4.

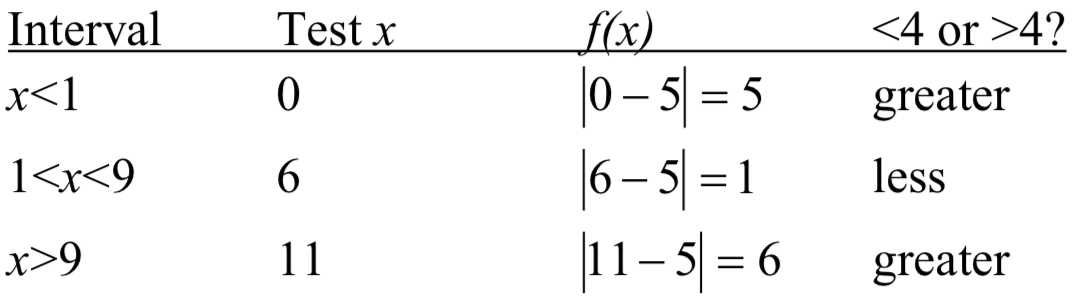
$2019-06-21 7.51.04.png$

Dado que $1 \le x \le 9$ es el único intervalo en el que la salida en el valor de prueba es menor a 4, podemos concluir que la solución a $\left|x-5\right| \le 4$ es $1 \le x \le 9$ .

Ejemplo $\PageIndex{7}$

Dada la función $f(x)=-\dfrac{1}{2} \left|4x-5\right|+3$ , determinar para qué $x$ valores los valores de la función son negativos.

Solución

Estamos tratando de determinar dónde $f(x) < 0$ , cuál es cuándo $-\dfrac{1}{2} \left|4x-5\right|+3<0$ . Comenzamos aislando el valor absoluto:

$-\dfrac{1}{2} \left|4x-5\right|<-3\nonumber$ cuando multiplicamos ambos lados por -2, invierte la desigualdad

$\left|4x-5\right|>6\nonumber$

A continuación resolvemos por la igualdad $\left|4x-5\right|=6$

$\begin{array}{l} {4x-5=6} \\ {4x=11} \\ {x=\dfrac{11}{4} } \end{array}\text{ or }\begin{array}{l} {4x-5=-6} \\ {4x=-1} \\ {x=\dfrac{-1}{4} } \end{array}\nonumber$

Ahora podemos elegir valores de prueba o esbozar una gráfica de la función para determinar en qué intervalos el valor original de la función es negativo. Observe que ni siquiera es realmente importante exactamente cómo se ve la gráfica, siempre y cuando sepamos que cruza el eje horizontal en $x=\dfrac{-1}{4}$ y $x=\dfrac{11}{4}$ , y que la gráfica se ha reflejado verticalmente.

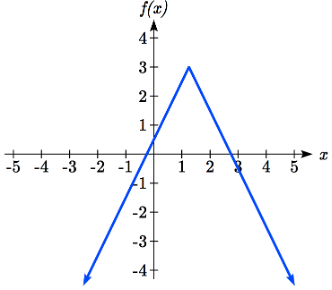
$Una gráfica de valores absolutos en forma de V con punto de esquina ligeramente a la derecha de 1 coma 3, con una intercepción horizontal entre x=negativo 1 y x=0, y otra entre x=2 y x=3.$

De la gráfica de la función, podemos ver que los valores de la función son negativos a la izquierda de la primera intercepción horizontal en $x=\dfrac{-1}{4}$ , y negativos a la derecha de la segunda intercepción en $x=\dfrac{11}{4}$ . Esto nos da la solución a la desigualdad:

$x<\dfrac{-1}{4} \quad \text{or}\quad x>\dfrac{11}{4}\nonumber$

En notación de intervalos, esto sería $\left(-\infty ,\dfrac{-1}{4} \right)\bigcup \left(\dfrac{11}{4} ,\infty \right)$

Ejercicio $\PageIndex{4}$

Resolver $-2\left|k-4\right|\le -6$

Contestar

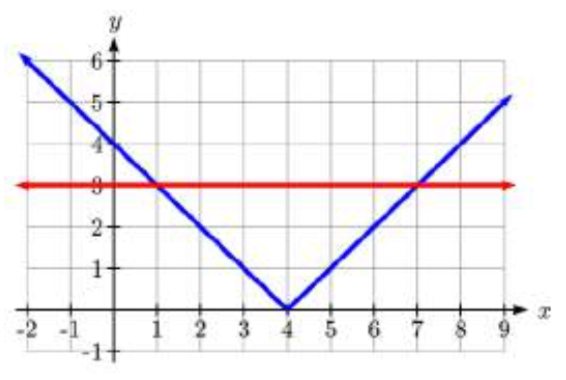$Una gráfica de valor absoluto de apertura hacia arriba con esquina en 4 coma 0, y una gráfica de y es igual a 3. Las gráficas se cruzan en 1 coma 3 y 7 coma 3.$ $-2\left|k-4\right|\le -6\nonumber$

$\left|k-4\right|\ge 3\nonumber$

Resolviendo la igualdad $\left|k-4\right|=3$ , k — 4 = 3 o k — 4 = —3, entonces k = 1 o k = 7.Usando una gráfica o valores de prueba, podemos determinar los intervalos que satisfacen la desigualdad son $k\le 1$ o $k\ge 7$ ; en notación de intervalos esto sería $\left(-\infty ,1\right]\cup \left[7,\infty \right)$

Temas Importantes de esta Sección

Las propiedades de la función de valor absoluto
Resolver ecuaciones de valor absoluto
Encontrar intercepciones
Resolver desigualdades de valor absoluto

Temas Importantes de esta Sección

Support Center

How can we help?