3.1: Funciones de alimentación

Última actualización
Guardar como PDF

Page ID: 116445

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Se corta un cuadrado de cartón, teniendo cada lado largo$L$. Si quisiéramos escribir una función para el área del cuadrado, con$L$ como entrada y el área como salida, puede recordar que el área de un rectángulo se puede encontrar multiplicando la longitud por el ancho. Como nuestra forma es cuadrada, el largo y el ancho son los mismos, dando la fórmula:

\[A(L)=L\cdot L=L^{2}\]

Así mismo, si quisiéramos una función para el volumen de un cubo con cada lado teniendo cierta longitud$L$, es posible que recuerde el volumen de una caja rectangular se puede encontrar multiplicando longitud por anchura por altura, que son todas iguales para un cubo, dando la fórmula:

\[V(L)=L\cdot L\cdot L=L^{3}\]

Estas dos funciones son ejemplos de funciones de potencia, funciones que son alguna potencia de la variable.

Definición: Función de potencia

Una función de potencia es una función que se puede representar en la forma

\[f(x)=x^{p}\]

Donde la base es una variable y el exponente,$p$, es un número.

Ejemplo$\PageIndex{1}$

¿Cuáles de nuestras funciones de kit de herramientas son funciones de potencia? (Este capítulo es parte de Precálculo: Una investigación de funciones © Lippman & Rasmussen 2017, y contiene contenido remezclado con permiso de Álgebra universitaria © Stitz & Zeager 2013. Este material está bajo una licencia Creative Commons CC-BY-SA.)

Soluciones

Las funciones constante e identidad son funciones de poder, ya que pueden escribirse como$f(x)=x^{0}$ y$f(x)=x^{1}$ respectivamente.

Las funciones cuadráticas y cúbicas son ambas funciones de potencia con potencias de número entero:$f(x)=x^{2}$ y$f(x)=x^{3}$.

Las funciones cuadradas recíprocas y recíprocas son ambas funciones de potencia con potencias negativas de número entero ya que pueden escribirse como$f(x)=x^{-1}$ y$f(x)=x^{-2}$.

Las funciones de raíz cuadrada y cúbica son funciones de potencia con potencias fraccionarias ya que pueden escribirse como$f(x) = x^{\dfrac{1}{2}}$ o$f(x) = x^{\dfrac{1}{3}}$

Ejercicio$\PageIndex{1}$

¿Qué punto (s) tienen en común las funciones de alimentación del kit de herramientas?

Contestar: (0, 0) y (1, 1) son comunes a todas las funciones de potencia.

Características de las funciones de potencia

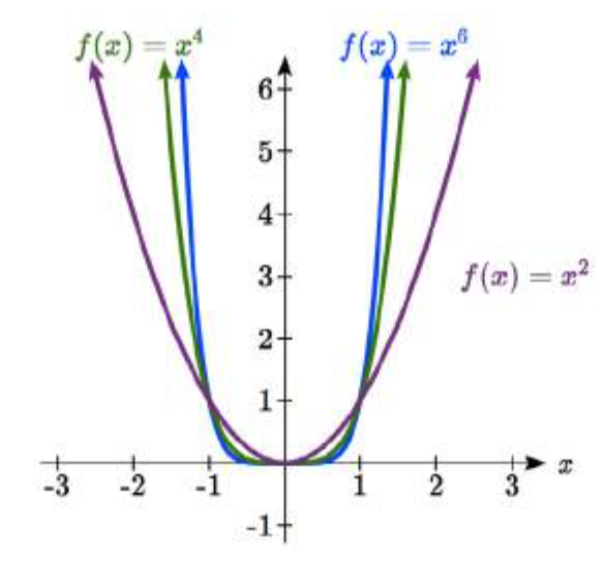$Gráficas de x^2, x^4 y x^6, todas en forma de U y pasando por el origen y 1 coma 1. x^6 es el más plano cerca del origen y más empinado del origen; x^2 es el más redondeado cerca del origen y menos empinado lejos del origen.$ A la derecha se muestran las gráficas de$f(x)=x^{2}$,, y$f(x)=x^{4}$$f(x)=x^{6}$, todos incluso los poderes de números enteros. Observe que todas estas gráficas tienen una forma bastante similar, muy similar al kit de herramientas cuadráticas, pero a medida que aumenta el poder las gráficas se aplanan un poco cerca del origen, y se vuelven más pronunciadas lejos del origen.

Para describir el comportamiento a medida que los números se hacen cada vez más grandes, usamos la idea de infinito. El símbolo para el infinito positivo es$\infty$, y$-\infty$ para el infinito negativo. Cuando decimos que “se$x$ acerca al infinito”, que puede escribirse simbólicamente como$x \to \infty$, estamos describiendo un comportamiento —estamos diciendo que$x$ se está haciendo grande en la dirección positiva.

Con las funciones de potencia par, a medida que el$x$ se vuelve grande en la dirección positiva o negativa, los valores de salida se convierten en números positivos muy grandes. Equivalentemente, podríamos describir esto diciendo que a medida que se$x$ acerca al infinito positivo o negativo, los$f(x)$ valores se acercan al infinito positivo. En forma simbólica, podríamos escribir: as$x \to \pm \infty$,$f(x) \to \infty$.

Aquí se muestran las gráficas de$f(x)=x^{3}$,, y$f(x)=x^{5}$$f(x)=x^{7}$, todos los poderes de números enteros impares. Observe que todas estas gráficas se parecen al kit de herramientas cúbicas, pero nuevamente a medida que aumenta la potencia, las gráficas se aplanan cerca del origen y se vuelven más pronunciadas lejos del origen.

$Gráficas de x^3, x^5 y x^7, todas aumentando rápidamente al principio, aplanándose cerca del origen, luego aumentando nuevamente, pasando por 1 coma 1. x^7 es el más plano cerca del origen y más empinado del origen; x^3 es el más redondeado cerca del origen y menos empinado lejos del origen.$

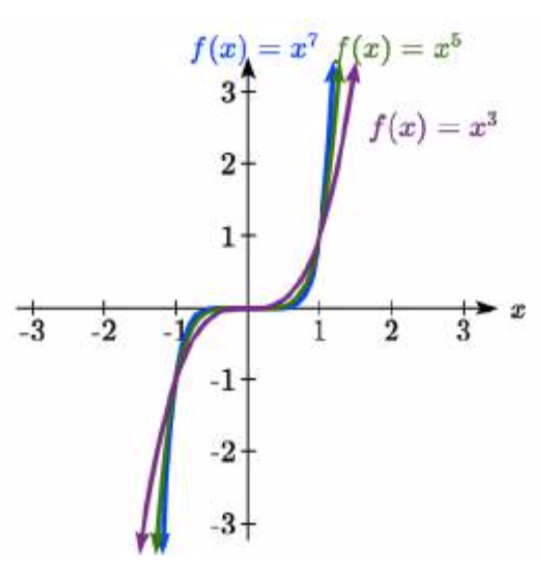
Para estas extrañas funciones de poder, a medida que$x$ se acerca al infinito negativo,$f(x)$ se acerca al infinito negativo. Al$x$ acercarse al infinito positivo,$f(x)$ se acerca al infinito positivo. En forma simbólica escribimos: como$x \to - \infty$,$f(x) \to - \infty$ y como$x \to \infty$,$f(x) \to \infty$.

Definición: comportamiento a largo plazo

El comportamiento de la gráfica de una función ya que la entrada toma grandes valores negativos$x \to - \infty$, y grandes valores positivos,$x \to \infty$, se conoce como el comportamiento a largo plazo de la función.

Ejemplo$\PageIndex{2}$

Describir el comportamiento a largo plazo de la gráfica de$f(x)=x^{8}$.

Solución

Dado que$f(x)=x^{8}$ tiene un poder entero, incluso, esperaríamos que esta función se comporte algo así como la función cuadrática. A medida que la entrada se vuelve grande positiva o negativa, esperaríamos que la salida crezca sin atarse en la dirección positiva. En forma simbólica, como$x \to \pm \infty$,$f(x) \to \infty$.

Ejemplo$\PageIndex{3}$

Describir el comportamiento a largo plazo de la gráfica de$f(x)=-x^{9}$

Solución

Dado que esta función tiene toda una potencia impar, esperaríamos que se comporte un poco como la función cúbica. El negativo frente al$x^{9}$ provocará una reflexión vertical, por lo que a medida que los insumos crezcan grandes positivos, las salidas crecerán grandes en la dirección negativa, y a medida que los insumos crezcan grandes negativos, las salidas crecerán grandes en la dirección positiva. En forma simbólica, para el comportamiento a largo plazo escribiríamos: como$x \to \infty$,$f(x)\to - \infty$ y como$x\to - \infty$,$f(x) \to \infty$.

Puede usar palabras o símbolos para describir el comportamiento a largo plazo de estas funciones.

Ejercicio$\PageIndex{2}$

Describir en palabras y símbolos el comportamiento a largo plazo de$f(x)=-x^{4}$

Contestar: A medida que$x$ se acerca al infinito positivo y negativo,$f(x)$ se acerca al infinito negativo: como$x \to \pm \infty$,$f(x) \to -\infty$ por el giro vertical.

El tratamiento de las formas racionales y radicales de las funciones de poder se guardará para más adelante.

Polinomios

Un oleoducto estalla en el Golfo de México, provocando una mancha de petróleo de forma aproximadamente circular. El resbaladizo tiene actualmente 24 millas de radio, pero ese radio está aumentando 8 millas cada semana. Si quisiéramos escribir una fórmula para el área cubierta por la mancha de petróleo, podríamos hacerlo componiendo dos funciones juntas. El primero es una fórmula para el radio$r$,, del derrame, que depende del número de semanas, w, que hayan pasado.

Ojalá reconocieras que esta relación es lineal:

\[r(w)=24+8w\nonumber\]

Podemos combinar esto con la fórmula para el área,$A$, de un círculo:

\[A(r)=\pi r^{2}\nonumber \]

La composición de estas funciones da una fórmula para el área en términos de semanas:

\[A(w)=A(r(w))=A(24+8w)=\pi (24+8w)^{2}\nonumber \]

Multiplicar esto da la fórmula

\[A(w)=576\pi +384\pi w+64\pi w^{2}\nonumber \]

Esta fórmula es un ejemplo de un polinomio. Un polinomio es simplemente la suma de términos cada uno que consiste en una función de potencia estirada verticalmente o comprimida con potencia de número entero no negativa.

terminología de funciones polinómicas

Un polinomio es una función que se puede escribir como

\[f(x)=a_{0} +a_{1} x+a_{2} x^{2} +\cdots +a_{n} x^{n} \label{poly1}\]

Cada una de las$a_{i}$ constantes se llama coeficientes y puede ser positiva, negativa o cero, y ser números enteros, decimales o fracciones.
Un término del polinomio es cualquier pieza de la suma, es decir, cualquiera$a_{i} x^{i}$. Cada término individual es una función de poder transformada.
El grado del polinomio es el mayor poder de la variable que ocurre en el polinomio.
El término principal es el término que contiene la mayor potencia de la variable: el término con mayor grado.
El coeficiente principal es el coeficiente del término principal.

Debido a la definición del término “líder”, a menudo reorganizamos la Ecuación\ ref {poly1} para que las potencias sean descendentes.

\[f(x)=a_{n} x^{n} +.....+a_{2} x^{2} +a_{1} x+a_{0} \label{poly2}\]

Ejemplo$\PageIndex{4}$

Identificar el grado, término principal y coeficiente principal de estos polinomios:

$f(x)=3+2x^{2} -4x^{3}$
$g(t)=5t^{5} -2t^{3} +7t$
$h(p)=6p-p^{3} -2$

Solución

Para la función$f(x)$, el grado es 3, el poder más alto encendido$x$. El término principal es el término que contiene ese poder,$-4x^{3}$. El coeficiente principal es el coeficiente de ese término, -4.
Para$g(t)$, el grado es 5, el término principal es$5t^{5}$, y el coeficiente principal es 5.
Para$h(p)$, el grado es 3, el término principal es$-p^{3}$, por lo que el coeficiente principal es -1.

Definición: comportamiento a largo plazo de polinomios

Para cualquier polinomio, el comportamiento a largo plazo del polinomio coincidirá con el comportamiento a largo plazo del término principal.

Ejemplo$\PageIndex{5}$

¿Qué podemos determinar sobre el comportamiento a largo plazo y el grado de la ecuación para el polinomio graficado aquí?

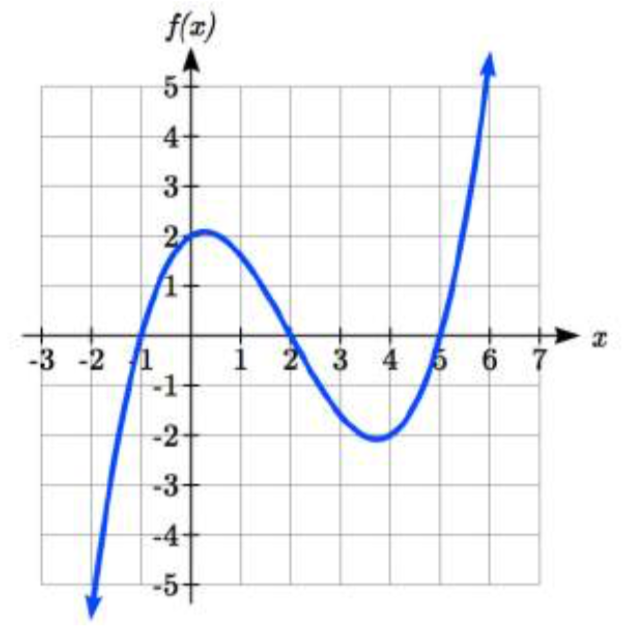
$Gráfico polinomial aumentando a 0 coma 2, disminuyendo a aproximadamente 3.8 coma negativa 2.1, luego aumentando.$

Solución

Dado que la salida crece grande y positiva a medida que las entradas crecen grandes y positivas, describimos el comportamiento a largo plazo simbólicamente escribiendo: as$x \to \infty$,$f(x) \to \infty$. De igual manera, como$x \to -\infty$,$f(x) \to -\infty$.

En palabras, podríamos decir que a medida que$x$ los valores se acercan al infinito, los valores de la función se acercan al infinito, y a medida que$x$ los valores se acercan al infinito negativo, los valores

Podemos decir que esta gráfica tiene la forma de una función de potencia de grado impar que no se ha reflejado, por lo que el grado del polinomio que crea esta gráfica debe ser impar, y el coeficiente inicial sería positivo.

Ejercicio$\PageIndex{3}$

Dada la función,$f(x)=0.2(x-2)(x+1)(x-5)$ usa tus habilidades de álgebra para escribir la función en forma polinómica estándar (como una suma de términos) y determinar el término principal, el grado y el comportamiento a largo plazo de la función.

Contestar: El término principal es$0.2x^{3}$, por lo que es un polinomio de grado 3. A medida que se$x$ acerca al infinito (o se vuelve muy grande en la dirección positiva) se$f(x)$ acerca al infinito; como se$x$ acerca al infinito negativo (o se vuelve muy grande en la dirección negativa) se$f(x)$ acerca al infinito negativo. (Básicamente el comportamiento a largo plazo es el mismo que el de la función cubic).

Comportamiento a corto plazo

Las características de la gráfica como las intercepciones verticales y horizontales y los lugares en los que la gráfica cambia de dirección son parte del comportamiento a corto plazo del polinomio.

Al igual que con todas las funciones, la intercepción vertical es donde la gráfica cruza el eje vertical, y ocurre cuando el valor de entrada es cero. Dado que un polinomio es una función, sólo puede haber una intercepción vertical, que ocurre en el punto$(0, a_{0})$. Las intercepciones horizontales ocurren en los valores de entrada que corresponden con un valor de salida de cero. Es posible tener más de una intercepción horizontal.

Las intercepciones horizontales también se llaman ceros, o raíces de la función.

Ejemplo$\PageIndex{6}$

Dada la función polinómica$f(x)=(x-2)(x+1)(x-4)$, escrita en forma factorizada para su conveniencia, determine las intercepciones verticales y horizontales.

Solución

La intercepción vertical ocurre cuando la entrada es cero.

\[f(0)=(0-2)(0+1)(0-4)=8\nonumber \]

La gráfica cruza el eje vertical en el punto (0, 8).

Las intercepciones horizontales ocurren cuando la salida es cero.

\[0=(x-2)(x+1)(x-4)\nonumber \]cuando$x$ = 2, -1 o 4.

$f(x)$tiene ceros, o raíces, a$x$ = 2, -1 y 4.

La gráfica cruza el eje horizontal en los puntos (2, 0), (-1, 0) y (4, 0)

Observe que el polinomio del ejemplo anterior, que sería grado tres si se multiplicaba, tenía tres intercepciones horizontales y dos puntos de inflexión —lugares donde la gráfica cambia de dirección. Ahora haremos una declaración general sin justificarla —las razones quedarán claras más adelante en este capítulo.

intercepciones y puntos de inflexión de polinomios

Un polinomio de grado$n$ tendrá:

A lo sumo intercepciones$n$ horizontales. Un polinomio de grado impar siempre tendrá al menos uno.
En la mayor parte$n - 1$ de los puntos

Ejemplo$\PageIndex{7}$

¿Qué podemos concluir sobre la gráfica del polinomio que se muestra aquí?

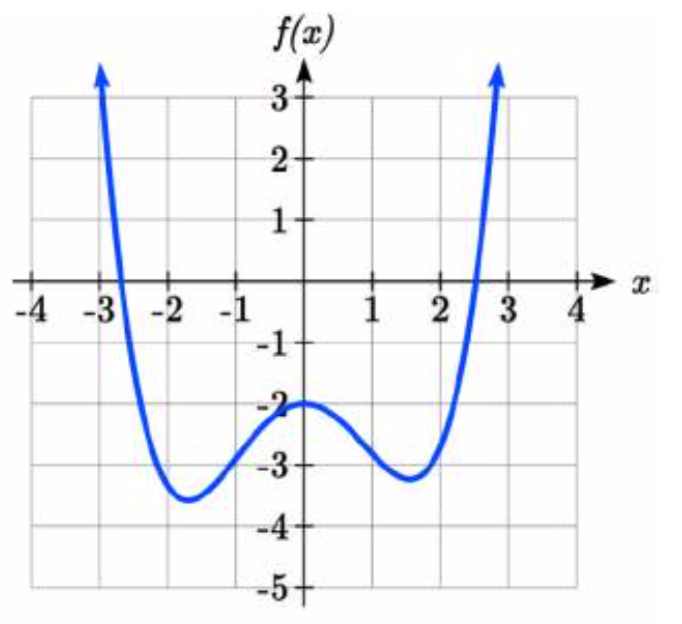
$Gráfico polinomial decreciente a aproximadamente (negativo 1,7, negativo 3.5), aumentando a 0 coma negativo 2, disminuyendo a 1.6 coma negativo 3.2, luego aumentando.$

Solución

Con base en el comportamiento a largo plazo, con la gráfica volviéndose grande positiva en ambos extremos de la gráfica, podemos determinar que esta es la gráfica de un polinomio de grado par. La gráfica tiene 2 intercepciones horizontales, lo que sugiere un grado de 2 o mayor, y 3 puntos de inflexión, lo que sugiere un grado de 4 o mayor. En base a esto, sería razonable concluir que el grado es parejo y al menos 4, por lo que probablemente sea un polinomio de cuarto grado.

Ejercicio$\PageIndex{4}$

Dada la función$f(x) = 0.2(x-2)(x+1)(x-5)$, determinar el comportamiento a corto plazo.

Contestar: Las intercepciones horizontales son (2, 0) (-1, 0) y (5, 0), la intercepción vertical es (0, 2) y hay 2 vueltas en la gráfica.

Temas Importantes de esta Sección

Funciones de alimentación
Polinomios
Coeficientes
Coeficiente principal
Término
Término principal
Grado de un polinomio
Comportamiento a largo plazo
Comportamiento a corto plazo