3.1.1E: Funciones de Potencia (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 116463

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

sección 3.1 EJERCICIO

Encuentre el comportamiento a largo plazo de cada función como$x \to \infty$ y$x \to -\infty$

1. $f(x)=x^{4}$

2. $f(x)=x^{6}$

3. $f(x)=x^{3}$

4. $f(x)=x^{5}$

5. $f(x)=-x^{2}$

6. $f(x)=-x^{4}$

7. $f(x)=-x^{7}$

8. $f(x)=-x^{9}$

Encuentra el grado y coeficiente principal de cada polinomio

9. $4x^{7}$

10. $5x^{6}$

11. $5-x^{2}$

12. $6+3x-4x^{3}$

13. $-2x^{4} - 3x^{2} + x-1$

14. $6x^{5} -2x^{4} + x^{2} + 3$

15. $(2x+3)(x-4)(3x+1)$

16. $(3x+1)(x+1)(4x+3)$

Encuentre el comportamiento a largo plazo de cada función como$x \to \infty$ y$x \to -\infty$

17. $-2x^{4} - 3x^{2} + x-1$

18. $6x^{5} -2x^{4} + x^{2} + 3$

19. $3x^{2} + x-2$

20. $-2x^{3} + x^{2} -x+3$

21. ¿Cuál es el número máximo de$x$ -intercepciones y puntos de inflexión para un polinomio de grado 5?

22. ¿Cuál es el número máximo de$x$ -intercepciones y puntos de inflexión para un polinomio de grado 8?

¿Cuál es el menor grado posible de la función polinómica que se muestra en cada gráfica?

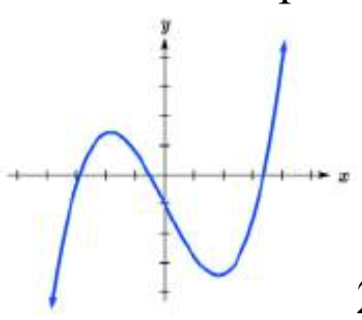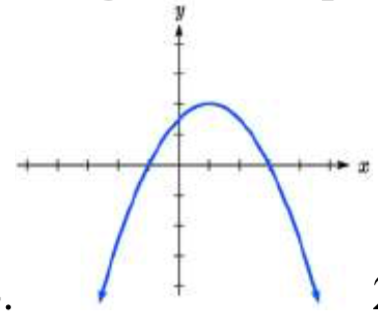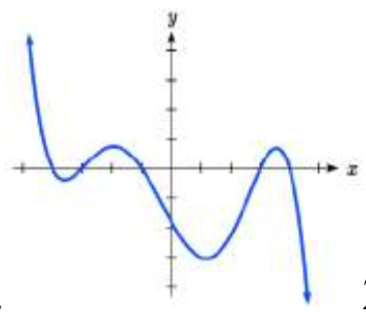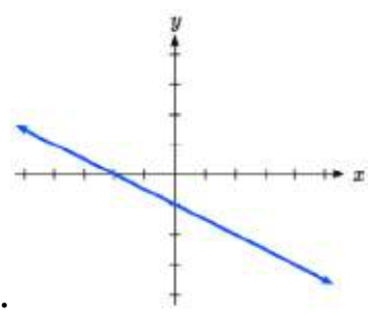
23. $2019-06-22 10.45.33.png$ 24 $2019-06-22 10.45.56.png$ .25. $2019-06-22 10.46.26.png$ 26. $2019-06-22 10.46.46.png$

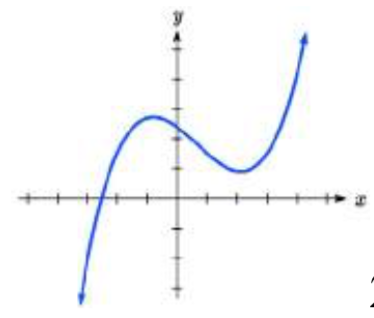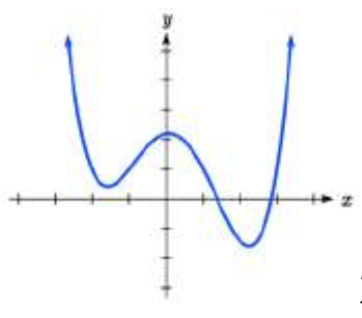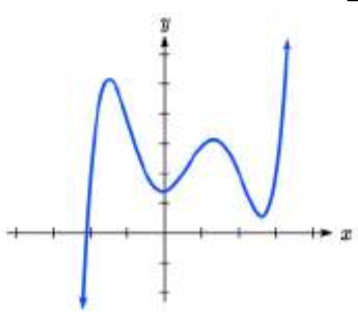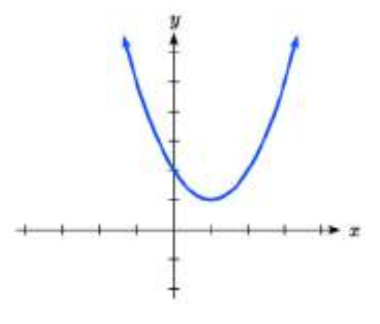
27. $2019-06-22 10.47.08.png$ 28. $2019-06-22 10.47.39.png$ 29. $2019-06-22 10.48.00.png$ 30. $2019-06-22 10.48.27.png$

Encuentra las intercepciones verticales y horizontales de cada función.

31. $f(t)=2(t-1)(t+2)(t-3)$

32. $f(x)=3(x+1)(x-4)(x+5)$

33. $g(n)=-2(3n-1)(2n+1)$

34. $k(u)=-3(4-n)(4n+3)$

Contestar

1. Como$x \to \infty$,$f(x) \to \infty$ As$x \to -\infty$,$f(x) \to \infty$

3. Como$x \to \infty$,$f(x) \to \infty$ As$x \to -\infty$,$f(x) \to -\infty$

5. Como$x \to \infty$,$f(x) \to -\infty$ As$x \to -\infty$,$f(x) \to -\infty$

7. Como$x \to \infty$,$f(x) \to -\infty$ As$x \to -\infty$,$f(x) \to \infty$

9. $7^{\text{th}}$Titulación, Coeficiente principal 4

11. $2^{\text{nd}}$Titulación, Coeficiente principal -1

13. $4^{\text{th}}$Titulación, Coeficiente principal -2

15. $3^{\text{rd}}$Titulación, Coeficiente principal 6

17. Como$x \to \infty$,$f(x) \to -\infty$ As$x \to -\infty$,$f(x) \to -\infty$

19. Como$x \to \infty$,$f(x) \to \infty$ As$x \to -\infty$,$f(x) \to \infty$

21. intercepciones: 5, puntos de inflexión: 4

23. 3

25. 5

27. 3

29. 5

31. Intercepciones horizontales (1, 0), (-2, 0), (3, 0) Intercepción vertical (0, 12)

33. Intercepciones horizontales (1/3, 0) (-1/2. 0) Intercepción vertical (0, 2)