3.6: Zeros complejos

Al encontrar los ceros de los polinomios, en algún momento te enfrentas al problema\(x^{2} =-1\). Si bien claramente no hay números reales que sean soluciones a esta ecuación, dejar las cosas ahí tiene cierta sensación de incompletitud. Para abordar eso, necesitaremos utilizar la unidad imaginaria,\(i\).

Definición: Número imaginario\(i\)

El número complejo más básico es\(i\), definido como\(i=\sqrt{-1}\), comúnmente llamado número imaginario. Cualquier múltiplo real de i también es un número imaginario.

Ejemplo\(\PageIndex{1}\)

Simplificar\(\sqrt{-9}\).

Solución

Podemos separarnos\(\sqrt{-9}\) como\(\sqrt{9} \sqrt{-1}\). Podemos tomar la raíz cuadrada de 9, y escribir la raíz cuadrada de -1 como\(i\).

\[\sqrt{-9} =\sqrt{9} \sqrt{-1} =3i \nonumber\]

Un número complejo es la suma de un número real y un número imaginario.

Definición: Números Complejos

Un número complejo es un número\(z=a+bi\), donde\(a\) y\(b\) son números reales

• \(a\)es la parte real del número complejo
• \(b\)es la parte imaginaria del número complejo\[i=\sqrt{-1}\]

Aritmética en números complejos

Antes de sumergirnos en los usos más complicados de los números complejos, asegurémonos de recordar la aritmética básica involucrada. Para sumar o restar números complejos, simplemente sumamos los términos similares, combinando las partes reales y combinando las partes imaginarias.

Ejemplo\(\PageIndex{2}\)

Agregar\(3-4i\) y\(2+5i\).

Solución

Añadiendo\((3-4i)+(2+5i)\), agregamos las partes reales y las partes imaginarias

\[3+2-4i+5i\nonumber\]

\[5+i \nonumber\]

Ejercicio\(\PageIndex{1}\)

Restar\(2+5i\) de\(3-4i\).

Contestar

\[(3-4i)-(2+5i)=1-9i \nonumber\]

También podemos multiplicar y dividir números complejos.

Ejemplo\(\PageIndex{3}\)

Multiplicar:\(4(2+5i)\).

Solución

Para multiplicar el número complejo por un número real, simplemente distribuimos como lo haríamos al multiplicar polinomios.

\[\begin{align*} 4(2+5i) &=4\cdot 2+4\cdot 5i \\[4pt] &=8+20i \end{align*}\]

Ejemplo\(\PageIndex{4}\)

Dividir\(\dfrac{(2+5i)}{(4-i)}\).

Solución

Para dividir dos números complejos, tenemos que idear una manera de escribir esto como un número complejo con una parte real y una parte imaginaria.

Iniciamos este proceso eliminando el número complejo en el denominador. Para ello, multiplicamos el numerador y denominador por un número complejo especial para que el resultado en el denominador sea un número real. El número por el que necesitamos multiplicar se llama el conjugado complejo, en el que se cambia el signo de la parte imaginaria.

Aquí, 4+ i es el conjugado complejo de 4— i. Por supuesto, obedeciendo nuestras reglas algebraicas, debemos multiplicar por 4+ i tanto en la parte superior como en la inferior.

\[\dfrac{(2+5i)}{(4-i)} \, \cdot \dfrac{(4+i)}{(4+i)} \nonumber \]

Para multiplicar dos números complejos, expandimos el producto como lo haríamos con polinomios (el proceso comúnmente llamado FOIL — “primero exterior interior último”). En el numerador:

\[(2+5i)(4+i)\nonumber\]Expandir
\[=8+20i+2i+5i^{2}\nonumber\] desde\(i=\sqrt{-1}\),\(i^{2} =-1\)
\[=8+20i+2i+5(-1)\nonumber\] simplificar
\[=3+22i\nonumber\]

Siguiendo el mismo proceso para multiplicar el denominador

\[(4-i)(4+i)\nonumber\]Ampliar
\[=(16-4i+4i-i^{2} )\nonumber\] Desde\(i=\sqrt{-1}\),\(i^{2} =-1\)
\[=(16-(-1))\nonumber\]
\[=17\nonumber\]

Combinando esto obtenemos\(\dfrac{3+22i}{17} =\dfrac{3}{17} +\dfrac{22i}{17}\)

Ejercicio\(\PageIndex{2}\)

Multiplicar\(3-4i\) y\(2+3i\).

Contestar

\[(3-4i)(2+3i)=18+i\nonumber\]

En el último ejemplo, se utilizó el conjugado de un número complejo

Definición: Conjugado complejo

El conjugado de un número complejo\(a+bi\) es el número\(a-bi\).

La notación comúnmente utilizada para la conjugación es una barra:\[\overline{a+bi}=a-bi\nonumber\]

Ceros Complejos de Polinomios

Los números complejos nos permiten escribir soluciones a ecuaciones cuadráticas que no tienen soluciones reales.

Ejemplo\(\PageIndex{5}\)

Encuentra los ceros de\(f(x)=x^{2} -2x+5\).

Solución

Usando la fórmula cuadrática,

\[x=\dfrac{2\pm \sqrt{(-2)^{2} -4(1)(5)} }{2(1)} =\dfrac{2\pm \sqrt{-16} }{2} =\dfrac{2\pm 4i}{2} =1\pm 2i. \nonumber\]

Ejercicio\(\PageIndex{3}\)

Encuentra los ceros de\(f(x)=2x^{2} +3x+4\).

Contestar

\[x=\dfrac{-3\pm \sqrt{(3)^{2} -4(2)(4)} }{2(2)} =\dfrac{-3\pm \sqrt{-23} }{4} =\dfrac{-3\pm i\sqrt{23} }{4} =\dfrac{-3}{4} \pm \dfrac{\sqrt{23} }{4} i \nonumber\]

Dos cosas son importantes a tener en cuenta. Primero, los ceros\(1+2i\) y\(1-2i\) son conjugados complejos. Este siempre será el caso cuando encontremos ceros no reales a una función cuadrática con coeficientes reales.

Segundo, podríamos escribir

\[f(x)=x^{2} -2x+5=\left(x-\left(1+2i\right)\right)\left(x-\left(1-2i\right)\right) \nonumber\]

si realmente quisiéramos, así que los Teoremas de Factor y Resto se mantienen.

¿Cómo sabemos si un polinomio general tiene ceros complejos? Hemos visto ejemplos de polinomios sin ceros reales; ¿puede haber polinomios sin ceros en absoluto? La respuesta a esa última pregunta, que proviene del Teorema Fundamental del Álgebra, es “No”.

Teorema: Teorema fundamental del álgebra

Un polinomio no constante\(f\) con coeficientes reales o complejos tendrá al menos un cero real o complejo.

Este teorema es un ejemplo de un teorema de “existencia” en matemáticas. Garantiza la existencia de al menos un cero, pero no proporciona ningún algoritmo que usar para encontrarlo.

Ahora supongamos que tenemos un polinomio\(f(x)\) de grado\(n\). El Teorema Fundamental del Álgebra garantiza al menos un cero\(z_{1}\), entonces el Teorema Factor garantiza que se\(f\) puede factorizar como\(f(x)=\left(x - z_{1} \right)q_{1} (x)\), donde el cociente\(q_{1} (x)\) será de grado\(n - 1\).

Si esta función no es constante, entonces le aplica el Teorema Fundamental del Álgebra, y podemos encontrar otro cero. Esto se puede repetir\(n\) veces.

Teorema: teorema de factorización compleja

Si\(f\) es un polinomio\(f\) con coeficientes reales o complejos con grado\(n \ge 1\), entonces\(f\) tiene exactamente ceros\(n\) reales o complejos, contando multiplicidades.

Si\(z_{1} ,z_{2} ,\ldots ,z_{k}\) son el cero distinto de\(f\) con multiplicidades\(m_{1} ,m_{2} ,\ldots ,m_{k}\) respectivamente, entonces

\[f(x)=a\left(x-z_{1} \right)^{m_{1} } \left(x-z_{2} \right)^{m_{2} } \cdots \left(x-z_{k} \right)^{m_{k} }\]

Ejemplo\(\PageIndex{6}\)

Encuentra todos los ceros reales y complejos de\(f(x)=12x^{5} -20x^{4} +19x^{3} -6x^{2} -2x+1\).

Solución

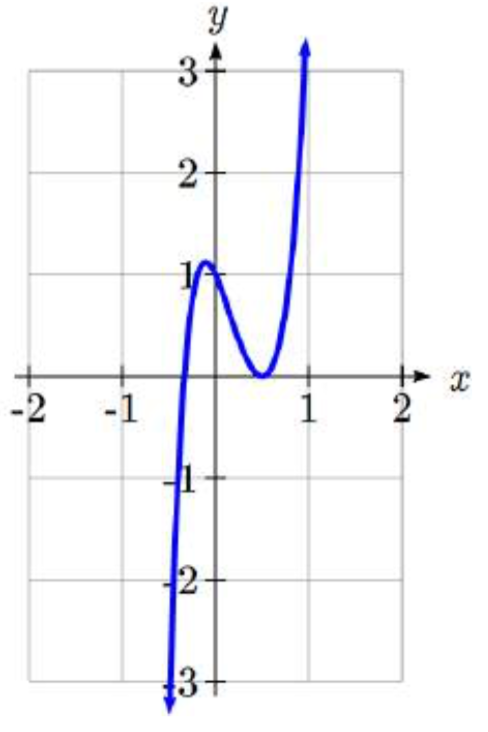Usando el Teorema de Raíces Racionales, las posibles raíces racionales reales son

\[\left\{\pm \dfrac{1}{1} ,\pm \dfrac{1}{2} ,\pm \dfrac{1}{3} ,\pm \dfrac{1}{4} ,\pm \dfrac{1}{6} ,\pm \dfrac{1}{12} \right\}\nonumber \]

Pruebas\(\dfrac{1}{2}\),

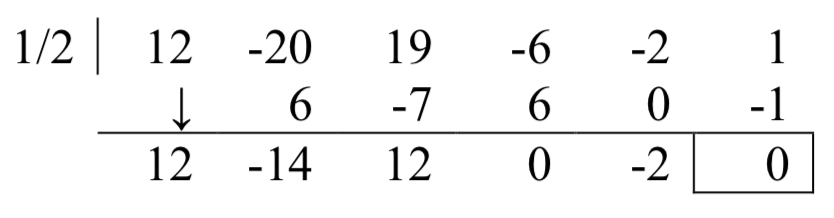
¡Éxito! Debido a que la gráfica rebota en esta intercepción, es probable que este cero tenga multiplicidad 2. Podemos probar de nuevo la división sintética para probarlo.

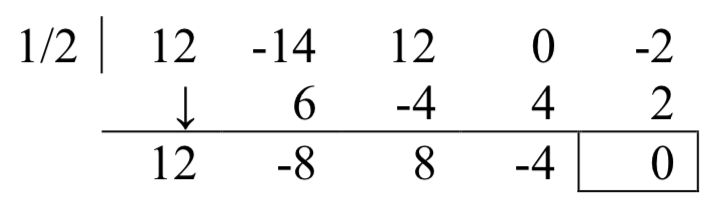
La otra raíz real parece ser\(-\dfrac{1}{3}\) o\(-\dfrac{1}{4}\). Pruebas\(-\dfrac{1}{3}\),

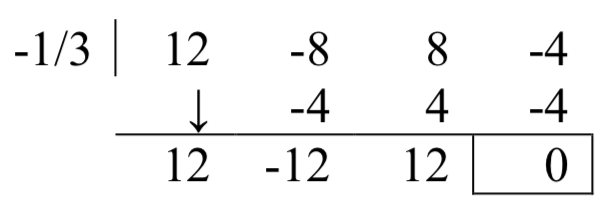
¡Excelente! Hasta el momento, hemos factorizado el polinomio para

\[f(x)=\left(x-\dfrac{1}{2} \right)^{2} \left(x+\dfrac{1}{3} \right)\left(12x^{2} -12x+12\right)=12\left(x-\dfrac{1}{2} \right)^{2} \left(x+\dfrac{1}{3} \right)\left(x^{2} -x+1\right)\nonumber \]

Podemos usar la fórmula cuadrática para encontrar los dos ceros restantes estableciendo\(x^{2} -x+1=0\), que probablemente sean ceros complejos.

\[x=\dfrac{1\pm \sqrt{(-1)^{2} -4(1)(1)} }{2(1)} =\dfrac{1\pm \sqrt{-3} }{2} =\dfrac{1\pm i\sqrt{3} }{2} \nonumber \]

Los ceros de la función son\(x=\dfrac{1}{2} ,-\dfrac{1}{3} ,\dfrac{1+i\sqrt{3} }{2} ,\dfrac{1-i\sqrt{3} }{2}\). Podríamos escribir la función totalmente factorizada como\(f(x)=12\left(x-\dfrac{1}{2} \right)^{2} \left(x+\dfrac{1}{3} \right)\left(x-\dfrac{1+i\sqrt{3} }{2} \right)\left(x-\dfrac{1-i\sqrt{3} }{2} \right)\).

Al factorizar un polinomio como lo hicimos al final del último ejemplo, decimos que se factoriza completamente sobre los números complejos, lo que significa que es imposible factorizar el polinomio más usando números complejos. Si quisiéramos factorizar la función sobre los números reales, nos habríamos detenido en\(f(x)=12\left(x-\dfrac{1}{2} \right)^{2} \left(x+\dfrac{1}{3} \right)\left(x^{2} -x+1\right)\). Dado que los ceros de\(x^{2} -x+1\) son irreales, llamamos\(x^{2} -x+1\) cuadrático irreducible, lo que significa que es imposible desglosarlo más usando números reales.

Resulta que un polinomio con coeficientes de número real puede ser factorizado en un producto de factores lineales correspondientes a los ceros reales de la función y factores cuadráticos irreducibles que dan los ceros no reales de la función. En consecuencia, cualquier ceros no reales vendrá en pares conjugados, así que si\(z\) es un cero del polinomio, así es\(\bar{z}\).

Ejercicio\(\PageIndex{4}\)

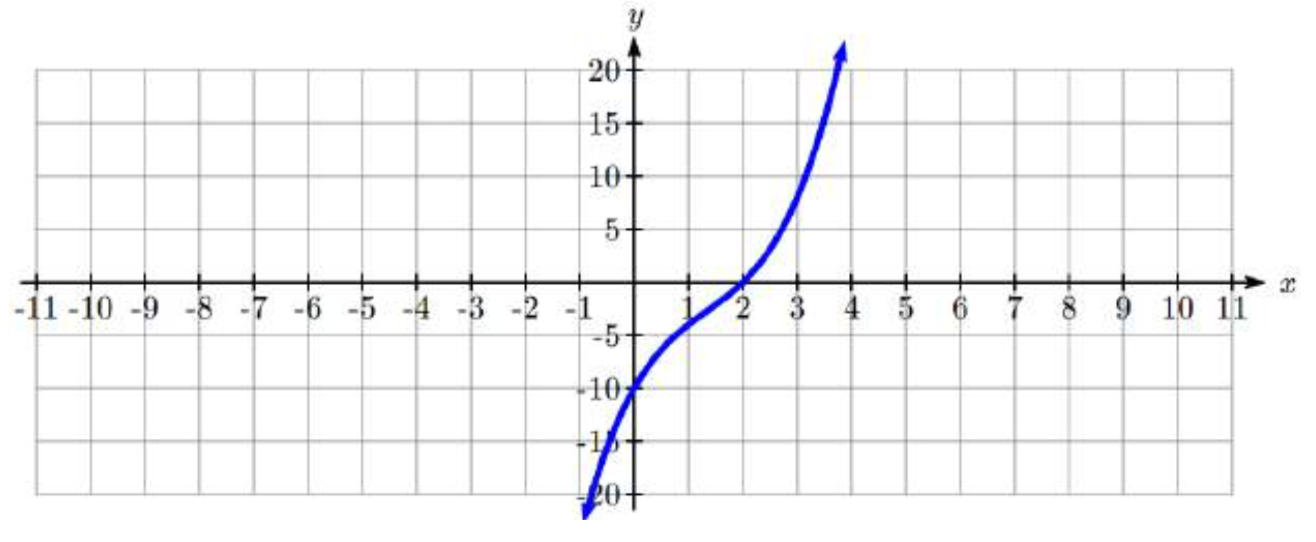
Encuentra los ceros reales y complejos de\(f(x)=x^{3} -4x^{2} +9x-10\).

Contestar

Cauchy's Bound nos limita al intervalo [-11, 11]. El teorema de raíces racionales da una lista de ceros potenciales:\(\left\{\pm 1,\pm 2,\pm 5,\pm 10\right\}\). Un gráfico rápido muestra que la raíz racional probable es\(x = 2\).

Verificando esto,

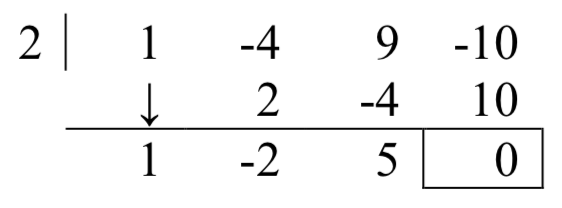
Entonces\(f(x)=(x-2)(x^{2} -2x+5)\)

Usando la fórmula cuadrática, podemos encontrar las raíces complejas de la cuadrática irreducible.

\[x=\dfrac{-(-2)\pm \sqrt{(-2)^{2} -4(1)(5)} }{2(1)} =\dfrac{2\pm \sqrt{-16} }{2} =\dfrac{-2\pm 4i}{2} =-1\pm 2i\nonumber \]

Los ceros de este polinomio son\(x=2,\; -1+2i,\; -1-2i\)

Temas Importantes de esta Sección

• Números complejos e imaginarios
• Encontrar ceros complejos de polinomios