3.7: Funciones racionales

Última actualización
Guardar como PDF

Page ID: 116483

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En las secciones anteriores, hemos construido polinomios basados en las funciones de potencia de número entero positivo. En esta sección, exploramos funciones basadas en funciones de potencia con potencias enteras negativas, llamadas funciones racionales.

Ejemplo$\PageIndex{1}$

Planeas conducir 100 millas. Encuentre una fórmula para el tiempo que tomará el viaje en función de la velocidad que conduce.

Solución

Tal vez recuerdes que multiplicar la velocidad por el tiempo te dará distancia. Si dejamos$t$ representar el tiempo de conducción en horas, y$v$ representamos la velocidad (velocidad o velocidad) a la que conducimos, entonces$vt$ = distancia. Dado que nuestra distancia es fija en 100 millas,$vt=100$. Resolver esta relación por el momento nos da la función que deseábamos:

\[t(v)=\dfrac{100}{v} =100v^{-1}\nonumber \]

Si bien este tipo de relación se puede escribir usando el exponente negativo, es más común verla escrita como una fracción.

Este ejemplo particular es uno de una relación inversamente proporcional —donde una cantidad es una constante dividida por la otra cantidad, como$y=\dfrac{5}{x}$.

Observe que esto es una transformación de la función recíproca del kit de herramientas,$f(x)=\dfrac{1}{x}$

Varios fenómenos naturales, como la fuerza gravitacional y el volumen del sonido, se comportan de manera inversamente proporcional al cuadrado de otra cantidad. Por ejemplo, el volumen,$V$, de un sonido escuchado a una$d$ distancia de la fuente estaría relacionado por$V=\dfrac{k}{d^{2} }$ por algún valor constante$k$.

Estas funciones son transformaciones de la función de conjunto de herramientas recíprocas al cuadrado$f(x)=\dfrac{1}{x^{2} }$.

Hemos visto las gráficas de la función recíproca básica y la función recíproca cuadrada de nuestro estudio de las funciones del kit de herramientas. Estas gráficas tienen varias características importantes.

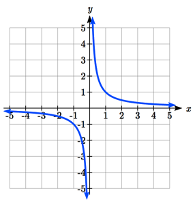
$Desde la izquierda la gráfica empieza plana justo por debajo de 0. A medida que x aumenta, y disminuye lentamente al principio y luego más rápidamente. A medida que x se acerca a 0 desde la izquierda, la gráfica disminuye rápidamente fuera de la ventana. Inmediatamente pasado 0, la gráfica disminuye rápidamente desde arriba de la ventana, disminuyendo rápidamente y primero luego más lentamente. 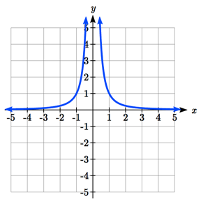A medida que x aumenta hacia la derecha, la gráfica se aplana, acercándose a 0.$ $Desde la izquierda la gráfica empieza plana justo por debajo de 0. A medida que x aumenta, y aumenta lentamente al principio y luego más rápidamente. A medida que x se acerca a 0 desde la izquierda, la gráfica aumenta rápidamente fuera de la ventana. Inmediatamente pasado 0, la gráfica disminuye rápidamente desde arriba de la ventana, disminuyendo rápidamente y primero luego más lentamente. A medida que x aumenta hacia la derecha, la gráfica se aplana, acercándose a 0.$

$f(x) = \dfrac{1}{x}$$f(x) = \dfrac{1}{x^2}$

Empecemos por mirar la función recíproca,$f(x)=\dfrac{1}{x}$. Como bien sabes, no se permite dividir por cero y por lo tanto cero no está en el dominio, y así la función está indefinida a una entrada de cero.

Comportamiento a corto plazo:

A medida que los valores de entrada se acercan a cero desde el lado izquierdo (tomando valores negativos muy pequeños), los valores de la función se vuelven muy grandes en la dirección negativa (en otras palabras, se acercan al infinito negativo).

Escribimos: como$x\to 0^{-}$,$f(x)\to -\infty$.

A medida que nos acercamos a cero desde el lado derecho (pequeños valores de entrada positivos), los valores de la función se vuelven muy grandes en la dirección positiva (acercándose al infinito).

Escribimos: como$x\to 0^{+}$,$f(x)\to \infty$.

Este comportamiento crea una asíntota vertical. Una asíntota es una línea a la que se acerca la gráfica. En este caso la gráfica se acerca a la línea vertical a$x = 0$ medida que la entrada se acerca a cero.

Comportamiento a largo plazo:

A medida que los valores de$x$ aproximación al infinito, los valores de función se acercan a 0

A medida que los valores de$x$ aproximación al infinito negativo, los valores de función se acercan a 0

Simbólicamente: como$x\to \pm \infty$,$f(x)\to 0$

En base a este comportamiento a largo plazo y en la gráfica podemos ver que la función se acerca a 0 pero nunca llega a 0, simplemente se “nivela” a medida que las entradas se hacen grandes. Este comportamiento crea una asíntota horizontal. En este caso la gráfica se acerca a la línea horizontal$f(x)=0$ ya que la entrada se vuelve muy grande en las direcciones negativa y positiva.

asíntotas verticales y horizontales

Una asíntota vertical de una gráfica es una línea vertical$x = a$ donde la gráfica tiende hacia el infinito positivo o negativo a medida que las entradas se acercan a. Como$x \to a$,$f(x) \to \pm \infty$.

Una asíntota horizontal de una gráfica es una línea horizontal$y=b$ donde la gráfica se acerca a la línea a medida que las entradas se hacen grandes. Como$x \to \pm \infty$,$f(x) \to b$.

Ejercicio$\PageIndex{1}$

Utilice la notación simbólica para describir el comportamiento a largo plazo y el comportamiento a corto plazo para la función cuadrada recíproca.

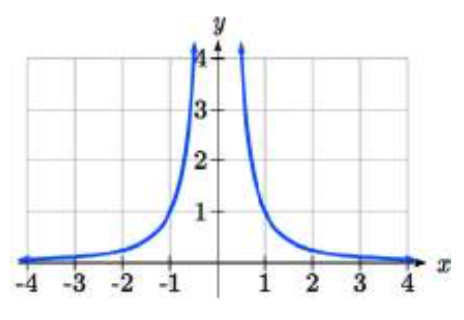
$Desde la izquierda la gráfica empieza plana justo por debajo de 0. A medida que x aumenta, y aumenta lentamente al principio y luego más rápidamente. A medida que x se acerca a 0 desde la izquierda, la gráfica aumenta rápidamente fuera de la ventana. Inmediatamente pasado 0, la gráfica disminuye rápidamente desde arriba de la ventana, disminuyendo rápidamente y primero luego más lentamente. A medida que x aumenta hacia la derecha, la gráfica se aplana, acercándose a 0.$

Responder

Comportamiento a largo plazo, como$x\to\pm\infty ,\quad f(x)\to 0$

Comportamiento a corto plazo, como$x\to 0,\quad f(x)\to\infty $ (no hay intercepciones horizontales o verticales)

Ejemplo$\PageIndex{2}$

Esboce una gráfica de la función recíproca desplazada dos unidades hacia la izquierda y tres unidades hacia arriba. Identificar las asíntotas horizontales y verticales de la gráfica, en su caso.

Solución

Transformar la gráfica izquierda 2 y arriba 3 resultaría en la función

$f(x)=\dfrac{1}{x+2} +3$, o equivalentemente, dando a los términos un denominador común,

$f(x)=\dfrac{3x+7}{x+2}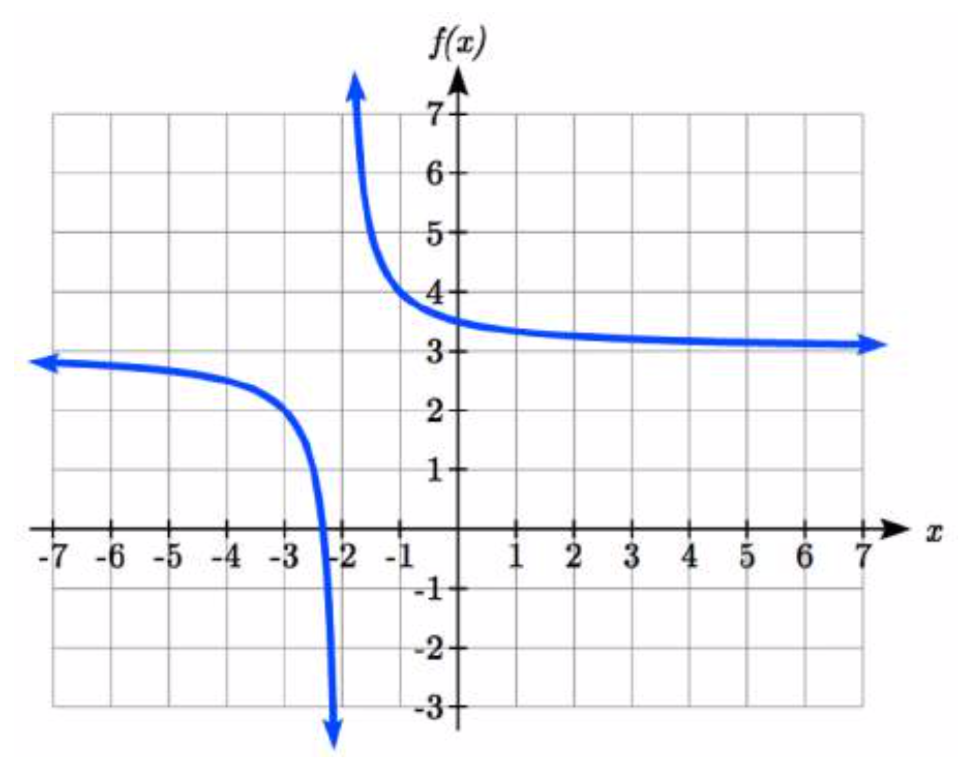$. $Desde la izquierda la gráfica empieza plana justo debajo de 3. A medida que x aumenta, y disminuye lentamente al principio y luego más rápidamente. A medida que x se acerca al negativo 2 desde la izquierda, la gráfica disminuye rápidamente fuera de la ventana. Inmediatamente pasado el negativo 2, la gráfica disminuye rápidamente desde arriba de la ventana, disminuyendo rápidamente y primero luego más lentamente. A medida que x aumenta hacia la derecha, la gráfica se aplana, acercándose a 3.$

Cambiar la función del kit de herramientas nos daría esta gráfica. Observe que esta ecuación no está definida en$x = -2$, y la gráfica también muestra una asíntota vertical en$x = -2$.

Como$x \to -2^{-}$,$f(x) \to -\infty$, y

como$x \to -2^{+}$,$f(x) \to \infty$

A medida que las entradas crecen grandes, la gráfica parece estar nivelándose a valores de salida de 3, lo que indica una asíntota horizontal en$y=3$.

Como$x \to \pm \infty$,$f(x) \to 3$.

Observe que las asíntotas horizontales y verticales se desplazan hacia la izquierda 2 y hacia arriba 3 junto con la función.

Ejercicio$\PageIndex{2}$

Esboza la gráfica y encuentra las asíntotas horizontales y verticales de la función cuadrada recíproca que se ha desplazado hacia la derecha 3 unidades y hacia abajo 4 unidades.

Responder

La función y las asíntotas se desplazan 3 unidades a la derecha y 4 unidades hacia abajo.

Como$x \to 3$,$f(x) \to \infty$ y como$x \to \pm \infty$,$f(x) \to -4$

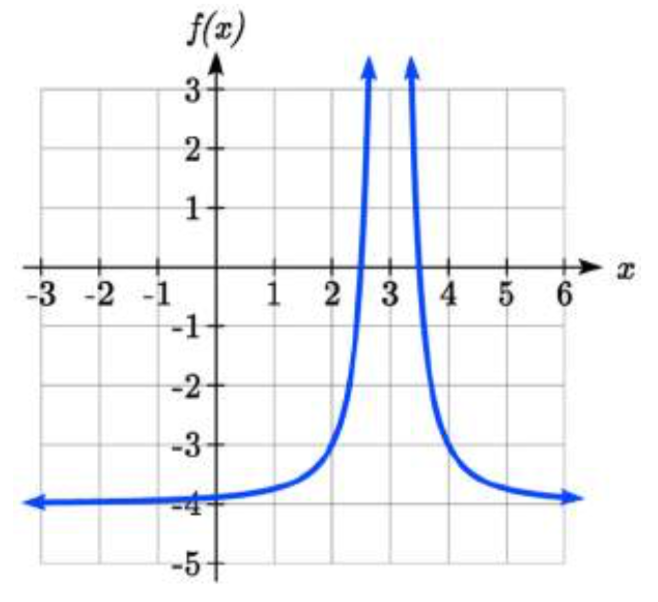
$Una gráfica que comienza plana, justo encima de la asíntota horizontal en y=2, luego aumenta curvándose hacia arriba, acercándose al infinito a medida que x se acerca a la asíntota vertical en 3. A la derecha de 3 la gráfica disminuye desde el infinito, luego comienza a aplanarse hacia la asíntota horizontal en y=2.$

En el ejemplo anterior, cambiamos una función de kit de herramientas de una manera que resultó en una función de la forma$f(x)=\dfrac{3x+7}{x+2}$. Este es un ejemplo de una función racional más general.

función racional

Una función racional es una función que se puede escribir como la proporción de dos polinomios,$P(x)$ y$Q(x)$.

\[f(x)=\dfrac{P(x)}{Q(x)} =\dfrac{a_{0} +a_{1} x+a_{2} x^{2} +\cdots +a_{p} x^{p} }{b_{0} +b_{1} x+b_{2} x^{2} +\cdots +b_{q} x^{q} }\]

Ejemplo$\PageIndex{3}$

Un gran tanque de mezcla contiene actualmente 100 galones de agua, en los que se han mezclado 5 libras de azúcar. Se abrirá un grifo vertiendo 10 galones por minuto de agua en el tanque al mismo tiempo que se vierte azúcar en el tanque a razón de 1 libra por minuto. Encuentra la concentración (libras por galón) de azúcar en el tanque después de$t$ minutos.

Solución

Observe que la cantidad de agua en el tanque está cambiando linealmente, al igual que la cantidad de azúcar en el tanque. Podemos escribir una ecuación independientemente para cada uno:

\[\text{water}=100+10t\nonumber\]
\[\text{sugar}=5+1t\nonumber\]

La concentración,$C$, será la proporción de libras de azúcar a galones de agua

\[C(t)=\dfrac{5+t}{100+10t}\nonumber \]

Hallazgo de asíntotas e intercepciones

Dada una función racional, como parte de investigar el comportamiento a corto plazo nos interesa encontrar cualquier asíntota vertical y horizontal, así como encontrar cualquier intercepción vertical u horizontal, como lo hemos hecho en el pasado.

Para encontrar asíntotas verticales, notamos que las asíntotas verticales en nuestros ejemplos ocurren cuando el denominador de la función es indefinido. Con una excepción, se producirá una asíntota vertical siempre que el denominador esté indefinido.

Ejemplo$\PageIndex{4}$

Encuentra las asíntotas verticales de la función$k(x)=\dfrac{5+2x^{2} }{2-x-x^{2} }$

Solución

Para encontrar las asíntotas verticales, determinamos dónde estará indefinida esta función estableciendo el denominador igual a cero:

\[\begin{array}{l} {2-x-x^{2} =0} \\ {(2+x)(1-x)=0} \\ {x=-2,\; 1} \end{array}\nonumber\]

Esto indica dos asíntotas verticales, lo que confirma una mirada a una gráfica.

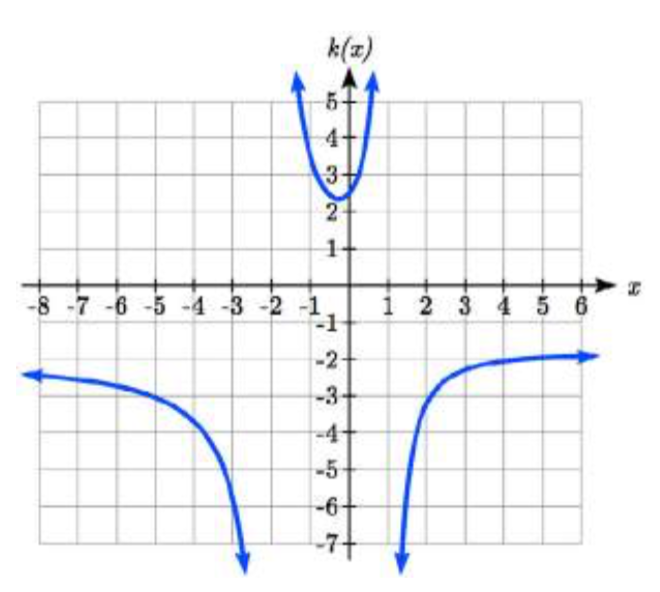
$Una gráfica que comienza disminuyendo lentamente, luego a medida que x se acerca al negativo 2 desde la izquierda, la gráfica disminuye rápidamente saliendo de la ventana. Derecha de x = negativo 2 la gráfica disminuye desde arriba de la ventana, luego gira y aumenta fuera de la ventana a medida que x se acerca a 1 desde la izquierda. Derecha de 1 la gráfica aumenta desde debajo de la ventana, luego comienza a aplanarse.$

La excepción a esta regla puede ocurrir cuando tanto el numerador como el denominador de una función racional son cero en la misma entrada.

Ejemplo$\PageIndex{5}$

Encuentra las asíntotas verticales de la función$k(x)=\dfrac{x-2}{x^{2} -4}$.

Solución

Para encontrar las asíntotas verticales, determinamos dónde estará indefinida esta función estableciendo el denominador igual a cero:

\[\begin{array}{l} {x^{2} -4=0} \\ {x^{2} =4} \\ {x=-2,\; 2} \end{array}\nonumber \]

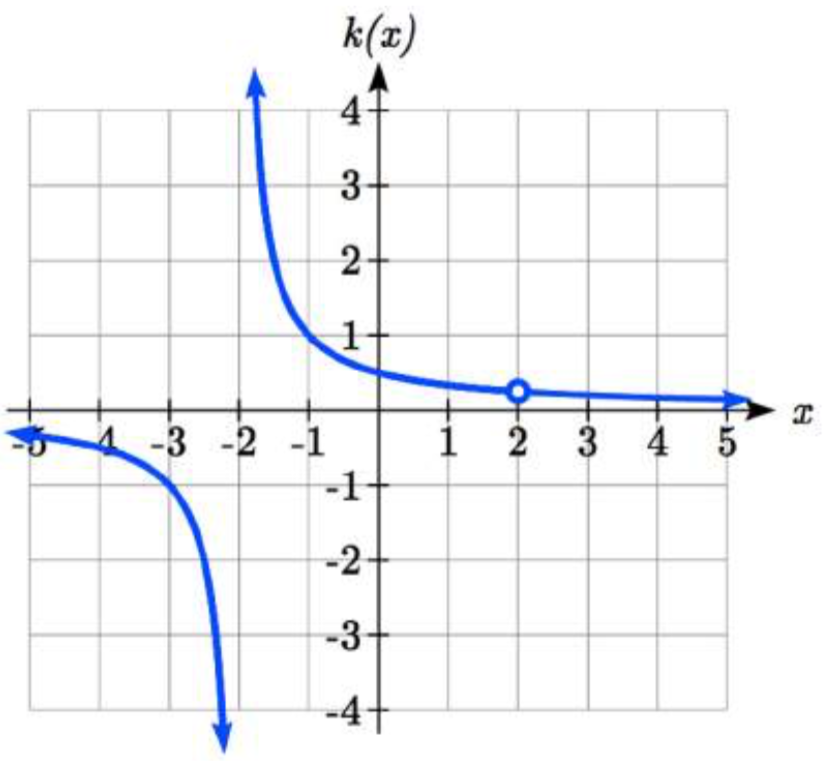$A medida que x se acerca al negativo 2 desde la izquierda, la gráfica se acerca al infinito negativo. A medida que x se acerca al negativo 2 desde la derecha, la gráfica se acerca al infinito positivo. Hay un círculo abierto en la gráfica donde x = 2.$ Sin embargo, el numerador de esta función también es igual a cero cuando$x = 2$. Debido a esto, la función seguirá estando indefinida en 2, ya que no$\dfrac{0}{0}$ está definida, pero la gráfica no tendrá una asíntota vertical en$x = 2$.

La gráfica de esta función tendrá la asíntota vertical en$x = -2$, pero en$x = 2$ la gráfica tendrá un agujero: un solo punto donde la gráfica no está definida, indicada por un círculo abierto.

asíntotas verticales y agujeros de funciones racionales

Las asíntotas verticales de una función racional ocurrirán donde el denominador de la función es igual a cero y el numerador no es cero.

Un agujero ocurre en la gráfica de una función racional si una entrada hace que tanto el numerador como el denominador sean cero. En este caso, factorizar el numerador y denominador y simplificar; si la expresión simplificada todavía tiene un cero en el denominador en la entrada original la función original tiene una asíntota vertical en la entrada, de lo contrario tiene un agujero.

Para encontrar asíntotas horizontales, nos interesa el comportamiento de la función a medida que la entrada crece grande, por lo que consideramos el comportamiento a largo plazo del numerador y denominador por separado. Recordemos que el comportamiento a largo plazo de un polinomio reflejará el del término principal. Asimismo, el comportamiento a largo plazo de una función racional reflejará el de la relación de los términos principales de las funciones numerador y denominador.

Hay tres resultados distintos cuando se realiza este análisis:

Caso 1: El grado del denominador > grado del numerador

Ejemplo$\PageIndex{6}$

\[f(x)=\dfrac{3x+2}{x^{2} +4x-5}\nonumber \]

En este caso, el comportamiento a largo plazo es$f(x)\approx \dfrac{3x}{x^{2} } =\dfrac{3}{x}$. Esto nos dice que a medida que las entradas crecen grandes, esta función se comportará de manera similar a la función$g(x)=\dfrac{3}{x}$. A medida que los insumos crecen grandes, los resultados se acercarán a cero, resultando en una asíntota horizontal en$y=0$.

Como$x\to \pm \infty$,$f(x)\to 0$

Caso 2: El grado del denominador < grado del numerador

Ejemplo$\PageIndex{7}$

\[f(x)=\dfrac{3x^{2} +2}{x-5}\nonumber \]

En este caso, el comportamiento a largo plazo es$f(x) \approx \dfrac{3x^{2} }{x} =3x$. Esto nos dice que a medida que las entradas crecen grandes, esta función se comportará de manera similar a la función$g(x)=3x$. A medida que las entradas crecen grandes, las salidas crecerán y no se nivelarán, por lo que esta gráfica no tiene asíntota horizontal.

Como$x\to \pm \infty$,$f(x)\to \pm \infty$, respectivamente.

Caso 3: El grado del denominador = grado del numerador

Ejemplo$\PageIndex{8}$

\[f(x)=\dfrac{3x^{2} +2}{x^{2} +4x-5}\nonumber \]

En este caso, el comportamiento a largo plazo es$f(x) \approx \dfrac{3x^{2} }{x^{2} } =3$. Esto nos dice que a medida que las entradas crecen grandes, esta función se comportará como la función$g(x)=3$, que es una línea horizontal. Como$x \to \pm \infty$,$f(x) \to 3$, resultando en una asíntota horizontal en$y=3$.

asíntota horizontal de funciones racionales

La asíntota horizontal de una función racional se puede determinar observando los grados del numerador y denominador.

Grado de denominador > grado de numerador: Asintota horizontal en$y=0$

Grado de denominador < grado de numerador: Sin asíntota horizontal

Grado de denominador = grado de numerador: Asintota horizontal en relación de coeficientes iniciales.

Ejemplo$\PageIndex{9}$

En el problema de concentración de azúcar de antes, creamos la ecuación

\[C(t)=\dfrac{5+t}{100+10t}\nonumber \]

Encontrar la asíntota horizontal e interpretarla en contexto del escenario.

Solución

Tanto el numerador como el denominador son lineales (grado 1), así como los grados son iguales, habrá una asíntota horizontal en la relación de los coeficientes principales. En el numerador, el término principal es$t$, con coeficiente 1. En el denominador, el término principal es 10$t$, con coeficiente 10. La asíntota horizontal estará en la relación de estos valores: As$t \to \infty$,$C(t) \to \dfrac{1}{10}$. Esta función tendrá una asíntota horizontal en$y=\dfrac{1}{10}$.

Esto nos dice que a medida que la entrada se hace grande, los valores de salida se acercarán a 1/10. En contexto, esto significa que a medida que pasa más tiempo, la concentración de azúcar en el tanque se acercará a una décima parte de libra de azúcar por galón de agua o 1/10 libras por galón.

Ejemplo$\PageIndex{10}$

Encuentra las asíntotas horizontales y verticales de la función

\[f(x)=\dfrac{(x-2)(x+3)}{(x-1)(x+2)(x-5)}\nonumber \]

Solución

Primero, tenga en cuenta que esta función no tiene entradas que hagan cero tanto el numerador como el denominador, por lo que no hay agujeros potenciales. La función tendrá asíntotas verticales cuando el denominador sea cero, haciendo que la función esté indefinida. El denominador será cero en$x$ = 1, -2 y 5, indicando asíntotas verticales en estos valores.

El numerador tiene grado 2, mientras que el denominador tiene grado 3. Dado que el grado del denominador es mayor que el del numerador, el denominador crecerá más rápido que el numerador, provocando que las salidas tiendan hacia cero a medida que las entradas se hacen grandes, y así como$x \to \pm \infty$,$f(x) \to 0$. Esta función tendrá una asíntota horizontal en$y=0$.

Ejercicio$\PageIndex{3}$

Encuentra las asíntotas verticales y horizontales de la función$f(x)=\dfrac{(2x-1)(2x+1)}{(x-2)(x+3)}$

Responder: asíntotas verticales en$x = 2$ y$x = -3$; asíntota horizontal en$y = 4$

Intercepta

Al igual que con todas las funciones, una función racional tendrá una intercepción vertical cuando la entrada sea cero, si la función se define en cero. Es posible que una función racional no tenga una intercepción vertical si la función está indefinida en cero.

Asimismo, una función racional tendrá intercepciones horizontales en las entradas que provoquen que la salida sea cero (a menos que esa entrada corresponda a un agujero). Es posible que no haya intercepciones horizontales. Dado que una fracción sólo es igual a cero cuando el numerador es cero, se producirán intercepciones horizontales cuando el numerador de la función racional sea igual a cero.

Ejemplo$\PageIndex{11}$

Encuentra las intercepciones de$f(x)=\dfrac{(x-2)(x+3)}{(x-1)(x+2)(x-5)}$

Solución

Podemos encontrar la intercepción vertical evaluando la función en cero

\[f(0)=\dfrac{(0-2)(0+3)}{(0-1)(0+2)(0-5)} =\dfrac{-6}{10} =-\dfrac{3}{5}\nonumber \]

Las intercepciones horizontales ocurrirán cuando la función sea igual a cero:

\[0=\dfrac{(x-2)(x+3)}{(x-1)(x+2)(x-5)}\nonumber \]Esto es cero cuando el numerador es cero

\[\begin{array}{l} {0=(x-2)(x+3)} \\ {x=2,\; -3} \end{array}\nonumber \]

Ejercicio$\PageIndex{4}$

Dada la función cuadrada recíproca que se desplaza hacia la derecha 3 unidades y hacia abajo 4 unidades, escribe esto como una función racional y encuentra las intercepciones horizontales y verticales y las asíntotas horizontales y verticales.

Responder

Para la función cuadrada recíproca transformada, encontramos la forma racional.

\[f(x) = \dfrac{1}{(x - 3)^2} - 4 = \dfrac{1 - 4(x - 3)^2}{(x - 3)^2} = \dfrac{1 - 4(x^2 - 6x + 9)}{(x - 3)(x - 3)} = \dfrac{-4x^2 + 24x - 35}{x^2 - 6x + 9}\nonumber \]

Dado que el numerador es el mismo grado que el denominador sabemos que como$x \to \pm \infty$,$f(x) \to -4$,$y = -4$ es la asíntota horizontal. A continuación, establecemos el denominador igual a cero para encontrar la asíntota vertical en$x = 3$, porque as$x \to 3$,$f(x) \to \infty$. Establecemos el numerador igual a 0 y encontramos que las intercepciones horizontales están en (2.5, 0) y (3.5, 0), luego evaluamos en 0 y la intercepción vertical está en$(0, \dfrac{-35}{9})$

Del ejemplo anterior, probablemente notó que el numerador de una función racional revela las intercepciones horizontales de la gráfica, mientras que el denominador revela las asíntotas verticales de la gráfica. Al igual que con los polinomios, los factores del numerador pueden tener potencias enteras mayores a uno. Felizmente, el efecto sobre la forma de la gráfica en esas intercepciones es el mismo que vimos con polinomios.

Cuando los factores del denominador tienen potencias enteras mayores que uno, el comportamiento en la asíntota vertical correspondiente reflejará una de las dos funciones recíprocas del kit de herramientas.

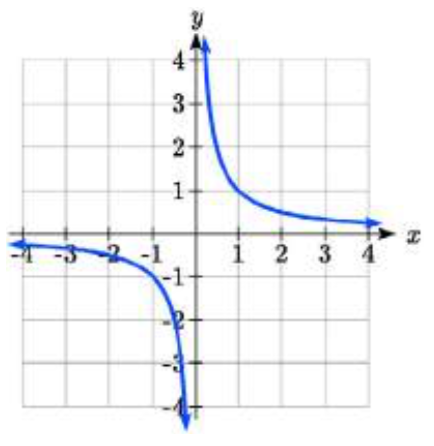
$2019-06-23 9.20.43.png$

Obtenemos este comportamiento cuando el grado del factor en el denominador es impar. La característica distintiva es que en un lado de la asíntota vertical la gráfica se dirige hacia el infinito positivo, y en el otro lado la gráfica se dirige hacia el infinito negativo.

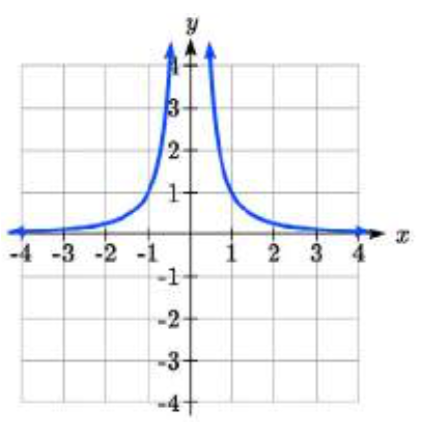
$2019-06-23 9.21.23.png$

Obtenemos este comportamiento cuando el grado del factor en el denominador es parejo. La característica distintiva es que la gráfica se dirige hacia el infinito positivo en ambos lados de la asíntota vertical, o se dirige hacia el infinito negativo en ambos lados.

F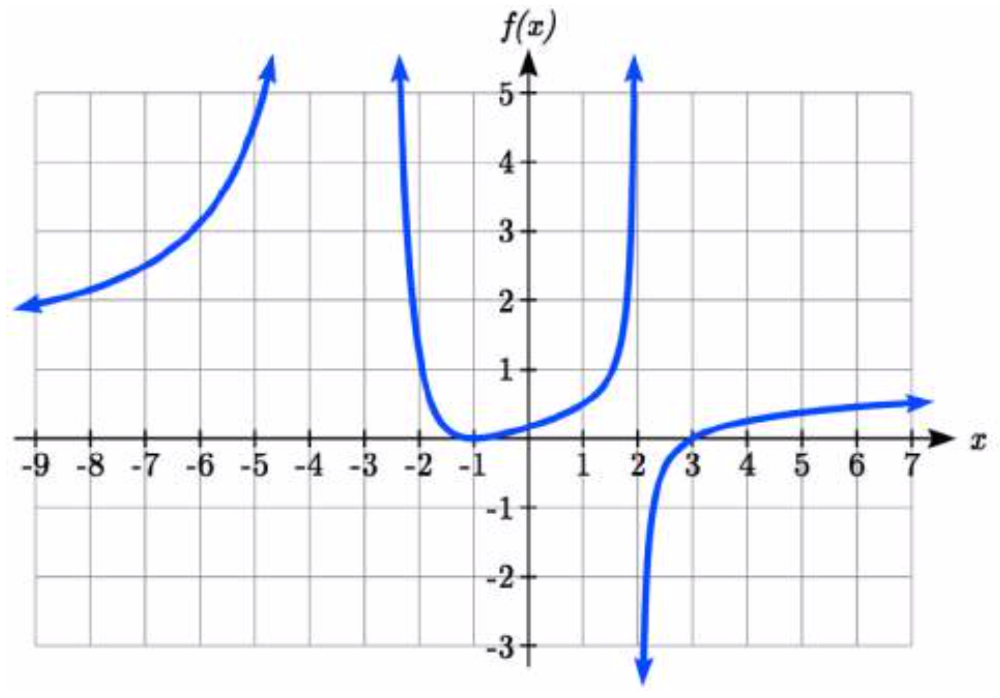 $La gráfica comienza aumentando, y a medida que x se acerca al negativo 3 desde cada lado, la gráfica se acerca al infinito positivo. A la derecha de x=negativo 3 la gráfica disminuye hacia abajo, toca el eje x en negativo 1, luego vuelve a aumentar. A medida que x se acerca a 2 desde la izquierda la gráfica se acerca al infinito. A medida que x se acerca a 2 desde la derecha la gráfica se acerca al infinito negativo. A la derecha de x=2 la gráfica aumenta, pasando por el eje x en x=3.$ o ejemplo, la gráfica de$f(x)=\dfrac{(x+1)^{2} (x-3)}{(x+3)^{2} (x-2)}$ se muestra aquí.

En la intercepción horizontal$x = -1$ correspondiente al$(x+1)^{2}$ factor del numerador, la gráfica rebota en la intercepción, consistente con la naturaleza cuadrática del factor.

En la intercepción horizontal$x = 3$ correspondiente al$(x-3)$ factor del numerador, la gráfica pasa por el eje como cabría esperar de un factor lineal.

En la asíntota vertical$x = -3$ correspondiente al$(x+3)^{2}$ factor del denominador, la gráfica se dirige hacia el infinito positivo en ambos lados de la asíntota, consistente con el comportamiento del$\dfrac{1}{x^{2} }$ kit de herramientas.

En la asíntota vertical$x = 2$ correspondiente al$(x-2)$ factor del denominador, la gráfica se dirige hacia el infinito positivo en el lado izquierdo de la asíntota y hacia el infinito negativo en el lado derecho, consistente con el comportamiento del kit de$\dfrac{1}{x}$ herramientas.

Ejemplo$\PageIndex{12}$

Esbozar una gráfica de$f(x)=\dfrac{(x+2)(x-3)}{(x+1)^{2} (x-2)}$.

Solución

Podemos comenzar nuestro boceto encontrando intercepciones y asíntotas. Evaluar la función en cero da la intercepción vertical:

\[f(0)=\dfrac{(0+2)(0-3)}{(0+1)^{2} (0-2)} =3\nonumber \]

Mirando cuando el numerador de la función es cero, podemos determinar que la gráfica tendrá intercepciones horizontales en$x = -2$ y$x = 3$. En cada uno, el comportamiento será lineal, con la gráfica pasando por la intercepción.

Mirando cuando el denominador de la función es cero, podemos determinar que la gráfica tendrá asíntotas verticales en$x = -1$ y$x = 2$.

Por último, el grado de denominador es mayor que el grado del numerador, diciéndonos que esta gráfica tiene una asíntota horizontal en$y = 0$.

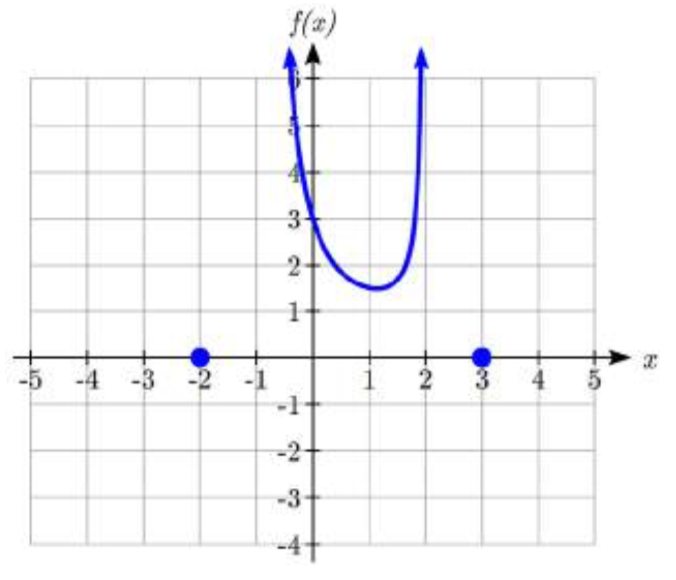
$Una gráfica incompleta, que muestra puntos en el eje x en negativo 2 y 3, y una porción en forma de U de la gráfica entre x = negativo 1 y x=2, tocando el eje y en y=3$

Para bosquejar la gráfica, podríamos comenzar trazando las tres intercepciones. Dado que la gráfica no tiene intercepciones horizontales entre las asíntotas verticales, y la intercepción vertical es positiva, sabemos que la función debe permanecer positiva entre las asíntotas, dejándonos rellenar la porción media de la gráfica.

Dado que el factor asociado a la asíntota vertical en$x = -1$ fue cuadrado, sabemos que la gráfica tendrá el mismo comportamiento en ambos lados de la asíntota. Dado que la gráfica se dirige hacia el infinito positivo a medida que las entradas se acercan a la asíntota de la derecha, la gráfica también se dirigirá hacia el infinito positivo a la izquierda. Para la asíntota vertical at$x = 2$, el factor no fue cuadrado, por lo que la gráfica tendrá un comportamiento opuesto a cada lado de la asíntota.

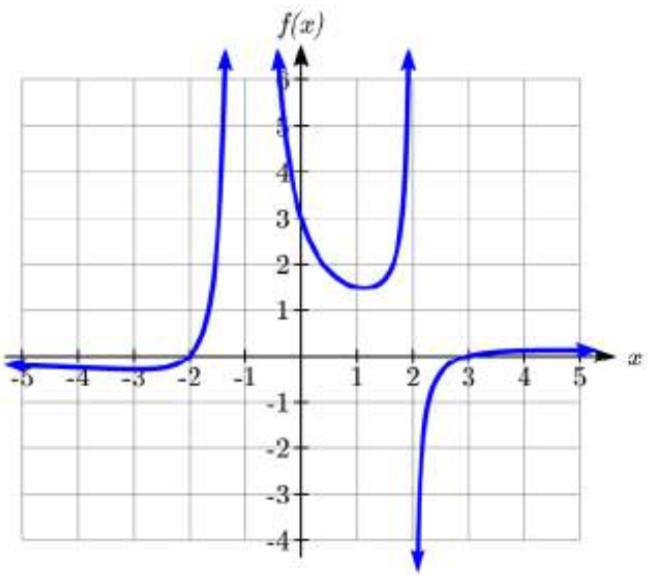
$Una gráfica que comienza plana por debajo de y=0, luego aumenta, pasando por el eje x en x=negativo 2, luego acercándose al infinito a medida que x se acerca al negativo 1. A la derecha del negativo 1 la gráfica disminuye desde fuera de la ventana, cruzando el eje y en y=3, y disminuyendo un poco más antes de aumentar, acercándose al infinito a medida que x se acerca a 2. A la derecha de 2, la gráfica aumenta desde fuera de la ventana, cruza el eje x en x=3, luego se nivela permaneciendo cerca de 0.$

Después de pasar por las intercepciones horizontales, la gráfica luego se nivelará hacia una salida de cero, como lo indica la asíntota horizontal.

Ejercicio$\PageIndex{5}$

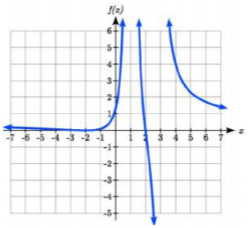
Dada la función$f(x)=\dfrac{(x+2)^{2} (x-2)}{2(x-1)^{2} (x-3)}$, utilizar las características de polinomios y funciones racionales para describir su comportamiento y esbozar la función.

Responder

Asíntota horizontal en$y = 1/2$.

Las asíntotas verticales están en$x = 1$, y$x = 3$.

Intercepción vertical en$(0, 4/3)$,

Horizontal intercepta$(2, 0)$ y$(-2, 0) (-2, 0)$ es un doble cero y la gráfica rebota en el eje en este punto.

$(2, 0)$es un solo cero y cruza el eje en este punto.

$La gráfica comienza justo debajo de la asíntota horizontal en y=una mitad, luego disminuye, tocando el eje x en negativo 2 luego aumenta hacia arriba, pasando por el eje y en 1 y acercándose al infinito a medida que x se acerca a 1. A la derecha de 1 la gráfica disminuye desde el infinito, pasando por x=2, y disminuyendo hacia infinito negativo a medida que x se acerca a 3. A la derecha de la 3 la gráfica disminuye desde el infinito positivo luego comienza a nivelarse hacia la asíntota horizontal en y = una mitad.$

Dado que una función racional escrita en forma factorizada tendrá una intercepción horizontal donde cada factor del numerador es igual a cero, podemos formar un numerador que pasará por un conjunto de intercepciones horizontales introduciendo un conjunto de factores correspondientes. De igual manera, dado que la función tendrá una asíntota vertical donde cada factor del denominador es igual a cero, podemos formar un denominador que producirá las asíntotas verticales introduciendo un conjunto de factores correspondiente.

escribir funciones racionales a partir de intercepciones y asíntotas

Si una función racional tiene intercepciones horizontales en$x=x_{1} ,x_{2} ,\ldots ,x_{n}$, y asíntotas verticales en$x=v_{1} ,v_{2} ,\ldots ,v_{m}$ entonces la función se puede escribir en la forma

\[f(x)=a\dfrac{(x-x_{1} )^{p_{1} } (x-x_{2} )^{p_{2} } \cdots (x-x_{n} )^{p_{n} } }{(x-v_{1} )^{q_{1} } (x-v_{2} )^{q_{2} } \cdots (x-v_{m} )^{q_{n} } }\]

donde las potencias p${}_{i}$ o q${}_{i}$ de cada factor pueden ser determinadas por el comportamiento de la gráfica en la intercepción o asíntota correspondiente, y el factor de estiramiento a puede determinarse dado un valor de la función distinto de la intercepción horizontal, o por la asíntota horizontal si es distinta de cero.

Ejemplo$\PageIndex{13}$

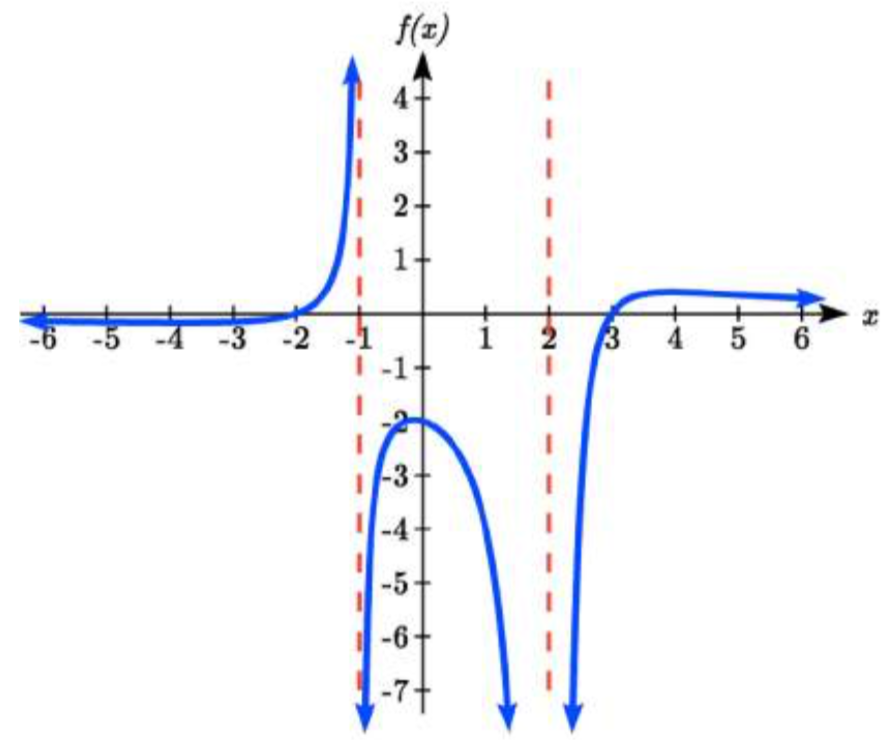
Escribe una ecuación para la función racional graficada aquí.

$Una gráfica que comienza plana por debajo del eje y, luego aumenta, pasando por el eje x en negativo 2, luego se acerca al infinito a medida que x se acerca a una asíntota vertical en x=negativo 1. A la derecha de la asíntota, la gráfica aumenta desde el infinito negativo, pasa el eje y en y= negativo 2, luego disminuye hacia el infinito a medida que x se acerca a otra asíntota vertical en x=2. A la derecha de esta asíntota la gráfica aumenta desde el infinito negativo, pasa por el eje x en x=3, aumenta ligeramente antes de disminuir lentamente hacia el eje x.$

Solución

La gráfica parece tener intercepciones horizontales en$x = -2$ y$x = 3$. En ambos, la gráfica pasa por la intercepción, sugiriendo factores lineales.

La gráfica tiene dos asíntotas verticales. El de$x = -1$ parece exhibir el comportamiento básico similar al de$\dfrac{1}{x}$, con la gráfica dirigiéndose hacia el infinito positivo en un lado y dirigiéndose hacia el infinito negativo en el otro.

La asíntota en$x = 2$ presenta un comportamiento similar al de$\dfrac{1}{x^{2} }$, con la gráfica dirigiéndose hacia el infinito negativo en ambos lados de la asíntota.

El uso de esta información indica una función de la forma

\[f(x)=a\dfrac{(x+2)(x-3)}{(x+1)(x-2)^{2} }\nonumber \]

Para encontrar el factor de estiramiento, podemos usar otro punto claro en la gráfica, como la intercepción vertical (0, -2):

\[\begin{array}{l} {-2=a\dfrac{(0+2)(0-3)}{(0+1)(0-2)^{2} } } \\ {-2=a\dfrac{-6}{4} } \\ {a=\dfrac{-8}{-6} =\dfrac{4}{3} } \end{array}\nonumber \]

Esto nos da una función final de$f(x)=\dfrac{4(x+2)(x-3)}{3(x+1)(x-2)^{2} }$

Asíntotas oblicuas

Anteriormente vimos gráficas de funciones racionales que no tenían asíntota horizontal, lo que ocurre cuando el grado del numerador es mayor que el grado del denominador. Podemos, sin embargo, describir con más detalle el comportamiento a largo plazo de una función racional.

Ejemplo$\PageIndex{14}$

Describir el comportamiento a largo plazo de$f(x)=\dfrac{3x^{2} +2}{x-5}$

Solución

Anteriormente exploramos esta función al discutir asíntotas horizontales. Encontramos que el comportamiento a largo plazo es$f(x) \approx \dfrac{3x^{2} }{x} =3x$, es decir$x\to \pm \infty$, que$f(x)\to \pm \infty$, respectivamente, y no hay asíntota horizontal.

Si tuviéramos que hacer polinomio división larga, podríamos obtener una mejor comprensión del comportamiento como$x\to \pm \infty$.

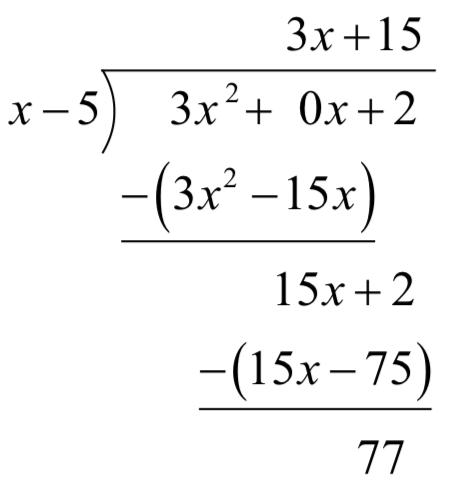
$2019-06-23 9.35.16.png$

Esto significa que se$f(x)=\dfrac{3x^{2} +2}{x-5}$ puede reescribir como$f(x)=3x+15+\dfrac{77}{x-5}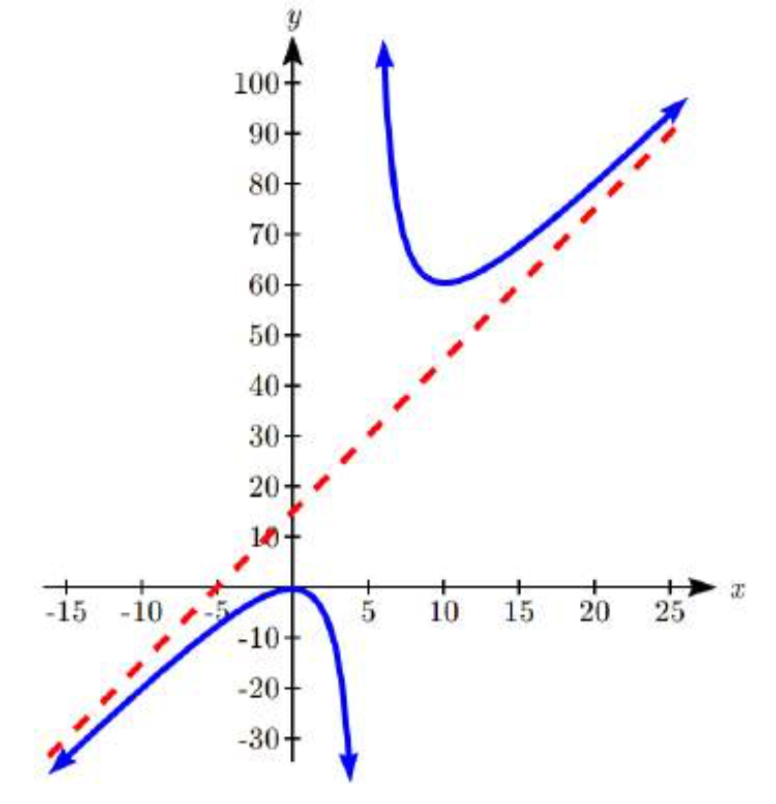$. $Una línea discontinua muestra la asíntota oblicua, pasando por el eje x en negativo 5 y el eje y en 15. La gráfica principal comienza justo debajo y casi paralela a la asíntota, luego se separa, tocando el origen antes de disminuir hacia el infinito a medida que x se acerca a 5. A la derecha de 5 la gráfica disminuye desde el infinito positivo, luego comienza a aumentar, acercándose y llegando a ser casi paralela a la asíntota oblicua.$

Como$x \to \pm \infty$, el término se$\dfrac{77}{x-5}$ volverá muy pequeño y se acercará a cero, volviéndose insignificante. El resto describe$3x+15$ entonces el comportamiento a largo plazo de la función: as$x\to \pm \infty$,$f(x) \to 3x+15$.

Llamamos a esta ecuación$y=3x+15$ la asíntota oblicua de la función.

En la gráfica, se puede ver cómo la función se acerca a la línea en el extremo izquierdo y extremo derecho.

asíntotas oblicuas

Para explorar el comportamiento a largo plazo de una función racional,

1) Realizar división polinómica larga (o división sintética)

2) El cociente describirá el comportamiento asintótico de la función

Cuando este resultado es una línea, lo llamamos asíntota oblicua, o asíntota inclinada.

Ejemplo$\PageIndex{15}$

Encuentra la asíntota oblicua de$f(x)=\dfrac{-x^{2} +2x+1}{x+1}$

Solución

Realización de división larga polinomial:

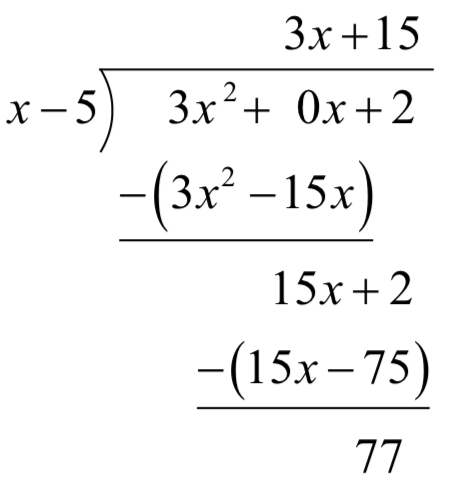
$2019-06-23 9.39.12.png$

Esto nos permite reescribir la función como

\[f(x)=-x+3-\dfrac{2}{x+1}\nonumber\]. 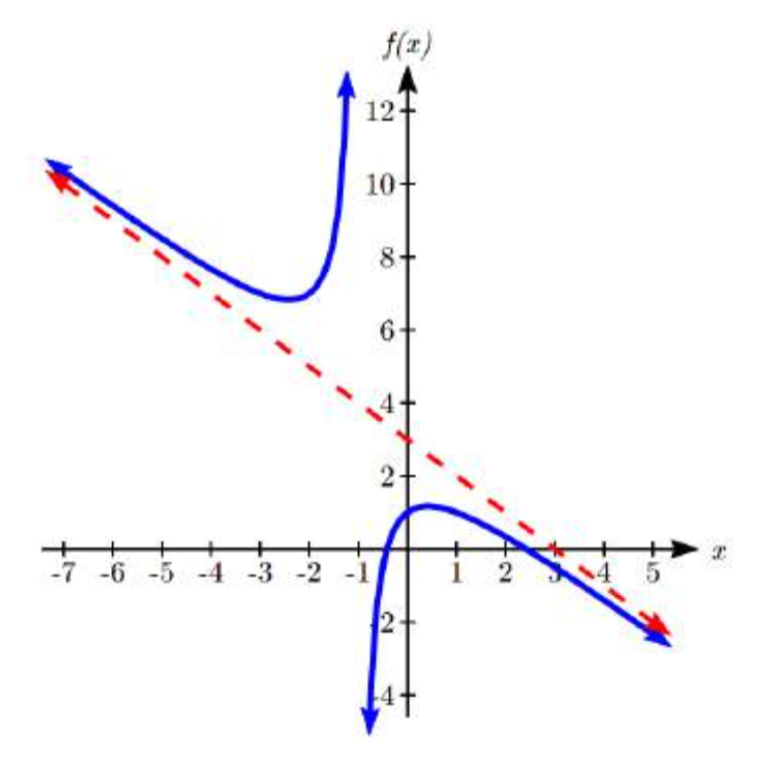$Una línea discontinua muestra la asíntota oblicua, una línea decreciente que pasa por el eje y en 3 y el eje x en 3. La gráfica principal comienza justo arriba y casi paralela a la asíntota, luego se separa, aumentando hacia el infinito a medida que x se acerca al negativo 1. A la derecha del negativo 1 la gráfica aumenta desde el infinito negativo, cruza el eje y en 1, luego disminuye, acercándose y llegando a ser casi paralela a la asíntota oblicua.$

El cociente,$y=-x+3$, es la asíntota oblicua de$f(x)$. Al igual que las funciones que vimos antes se acercaron a su asíntota horizontal a largo plazo, esta función se acercará a esta asíntota oblicua a largo plazo.

Ejercicio$\PageIndex{6}$

Encuentra la asíntota oblicua de$f(x)=\dfrac{1+7x-2x^{2} }{x-2}$

Responder

Usando división larga:

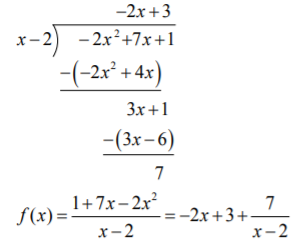
$clipboard_e9403dec7a347abb39ee11ca7bed8fa19.png$

La asíntota oblicua es$y=-2x+3$

Si bien nos ocupamos principalmente de asíntotas oblicuas, este mismo enfoque puede describir otro comportamiento asintótico.

Ejemplo$\PageIndex{16}$

Describir la forma a largo plazo de$f(x)=\dfrac{-x^{3} -x^{2} +4x+2}{x+1}$

Solución

Podríamos reescribir esto usando división larga como $Una curva discontinua muestra la asíntota, una parábola de apertura hacia abajo que aumenta hasta el punto 0 coma 4 luego disminuye. La gráfica principal comienza justo por encima de la asíntota curva, luego diverge, aumentando hacia el infinito a medida que x se acerca al negativo 1. A la derecha del negativo 1 la gráfica aumenta desde el infinito negativo, pasa por el eje y en 2, luego disminuye, acercándose a la asíntota curva.$

\[f(x)=-x^{2} +4+\dfrac{2}{x+1}\nonumber \]

El solo mirar el cociente nos da la asíntota,$y=-x^{2} +4$.

Esto sugiere que a la larga, la función se comportará como una parábola de apertura hacia abajo. La función también tendrá una asíntota vertical en$x=-1$.

Temas Importantes de esta Sección

Inversamente proporcional; Función recíproca del kit de herramientas

Inversamente proporcional al cuadrado; Función de kit de herramientas al cuadrado recíproco

Aíntotas horizontales

Aíntotas Verticales

Funciones racionales

Encontrar intercepciones, asíntotas y agujeros.

Dada ecuación esbozar la gráfica

Identificar una función a partir de su gráfica

Aíntotas oblicuas