4.2: Gráficas de Funciones Exponenciales

Última actualización
Guardar como PDF

Page ID: 116863

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Al igual que con las funciones lineales, la gráfica de una función exponencial está determinada por los valores para los parámetros en la fórmula de la función.

Para tener una idea del comportamiento de los exponenciales, comencemos por mirar más de cerca la función$f(x)=2^{x}$. Listado de una tabla de valores para esta función:

$x$	-3	-2	-1	0	1	2	3
$f(x)$	$\dfrac{1}{8}$	$\dfrac{1}{4}$	$\dfrac{1}{2}$	1	2	4	8

Observe que:

1. Esta función es positiva para todos los valores de$x$.
2. A$x$ medida que aumenta, la función crece cada vez más rápido (la tasa de cambio aumenta).
3. A medida que$x$ disminuye, los valores de la función se hacen más pequeños, acercándose
4. Este es un ejemplo de crecimiento exponencial.

Mirando la función$g(x)=\left(\dfrac{1}{2} \right)^{x}$

$x$	-3	-2	-1	0	1	2	3
$g(x)$	8	4	2	1	$\dfrac{1}{2}$	$\dfrac{1}{4}$	$\dfrac{1}{8}$

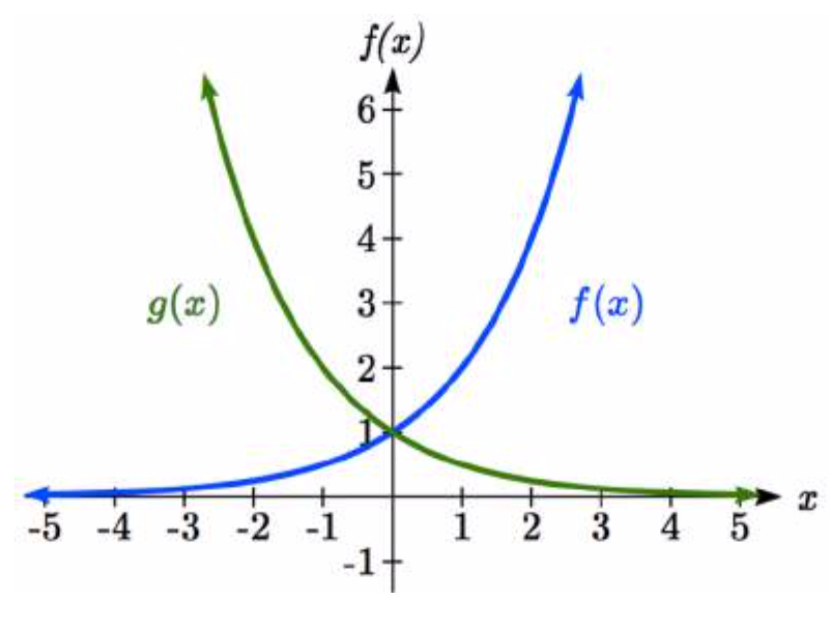
Tenga en cuenta que esta función también es positiva para todos los valores de$x$, pero en este caso crece a medida que$x$ disminuye, y disminuye hacia cero a medida que$x$ aumenta. Este es un ejemplo de decaimiento exponencial. Puede notar en la tabla que esta función parece ser el reflejo horizontal de la$f(x)=2^{x}$ tabla. Este es, de hecho, el caso:

$Dos gráficas en los mismos ejes. El primero, etiquetado f (x), comienza plano a la izquierda justo por encima del eje x y aumenta, curvándose hacia arriba a medida que x aumenta, pasando por el eje y en 1, y continuando curvándose hacia arriba. El segundo, etiquetado g (x), es el reflejo horizontal del primero. Disminuye rápidamente a la izquierda, y se vuelve menos empinada a medida que x aumenta, pasando por el eje y en 1 y comenzando a aplanarse hacia el eje x a medida que x aumenta.$ $f(-x)=2^{-x} =(2^{-1} )^{x} =\left(\dfrac{1}{2} \right)^{x} =g(x) \nonumber$

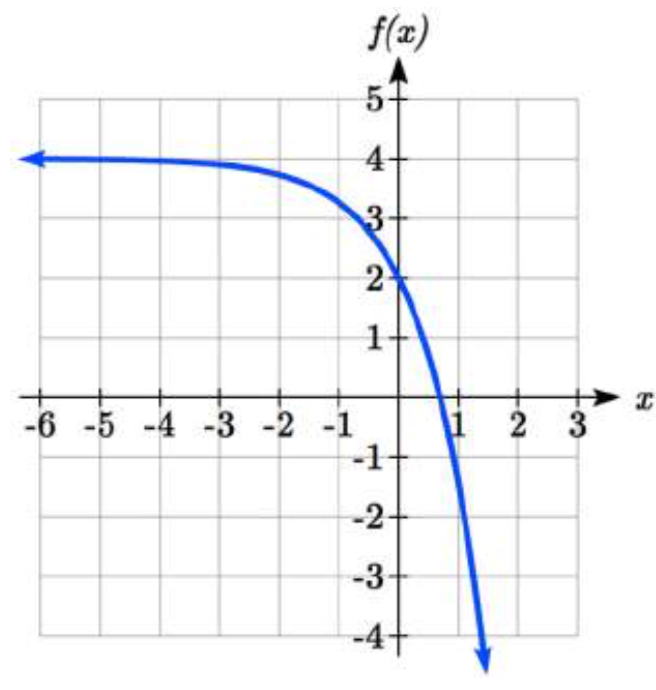
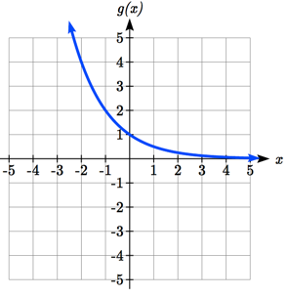
Mirar las gráficas también confirma esta relación.

Considerar una función de la forma$f(x)=ab^{x}$. Ya que$a$, al que llamamos el valor inicial en la última sección, es el valor de la función a una entrada de cero, nos$a$ dará la intercepción vertical de la gráfica.

De las gráficas anteriores, podemos ver que una gráfica exponencial tendrá una asíntota horizontal en un lado de la gráfica, y puede aumentar o disminuir, dependiendo del factor de crecimiento. Esta asíntota horizontal también nos ayudará a determinar el comportamiento a largo plazo y es fácil de determinar a partir de la gráfica.

El gráfico crecerá cuando la tasa de crecimiento sea positiva, lo que hará que el factor de crecimiento sea$b$ mayor a uno. Cuando es negativo, el factor de crecimiento será menor de uno.

características gráficas de funciones exponenciales

Gráficamente, en la función$f(x)=ab^{x}$

$a$es la intercepción vertical de la gráfica

$b$determina la velocidad a la que crece la gráfica. Cuando$a$ es positivo,

la función aumentará si$b > 1$
la función disminuirá si$0 < b < 1$

La gráfica tendrá una asíntota horizontal en$y = 0$

La gráfica será cóncava hacia arriba si$a > 0$; cóncava hacia abajo si$a < 0$.

El dominio de la función son todos los números reales

El rango de la función es$(0,\infty )$

Al esbozar la gráfica de una función exponencial, puede ser útil recordar que la gráfica pasará por los puntos (0,$a$) y (1,$ab$).

El valor$b$ determinará el comportamiento a largo plazo de la función:

Si$b > 1$, como$x \to \infty$,$f(x) \to \infty$ y como$x \to -\infty$,$f(x) \to 0$.

Si$0 < b < 1$, como$x\to \infty$,$f(x) \to 0$ y como$x \to -\infty$,$f(x) \to \infty$.

Ejemplo$\PageIndex{1}$

Dibuje una gráfica de$f(x)=4\left(\dfrac{1}{3} \right)^{x}$.

Solución

T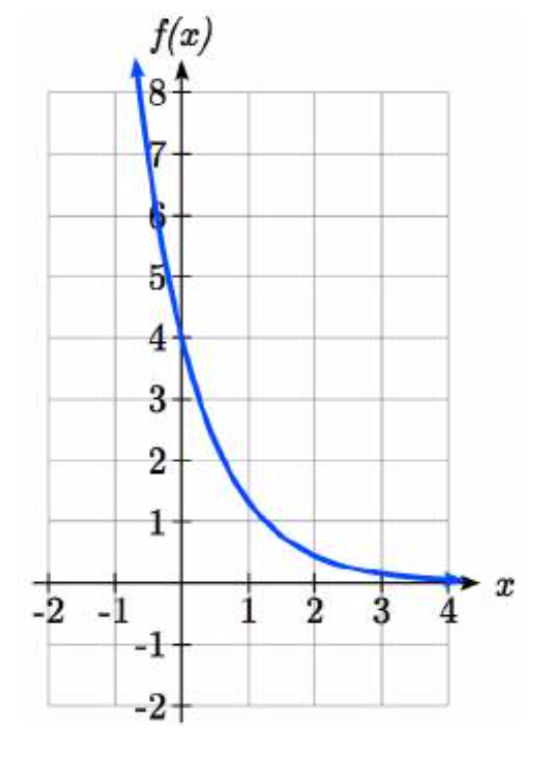 $Una gráfica que disminuye abrupta al principio luego se aplana a medida que x aumenta, pasando por 0 coma 4 y (1, cuatro tercios), luego se acerca al eje x a medida que aumenta x.$ su gráfica tendrá una intercepción vertical en (0,4), y pasará por el punto$\left(1,\dfrac{4}{3} \right)$. Ya que$b < 1$, la gráfica estará disminuyendo hacia cero. Ya que$a > 0$, la gráfica será cóncava hacia arriba.

También podemos ver en la gráfica el comportamiento a largo plazo: como$x\to \infty$,$f(x)\to 0$ y como$x\to -\infty$,$f(x)\to \infty$.

Para tener una mejor idea del efecto de$a$ y$b$ sobre la gráfica, examine los conjuntos de gráficos a continuación. El primer conjunto muestra diversas gráficas, donde a sigue siendo la misma y solo cambiamos el valor por$b$.

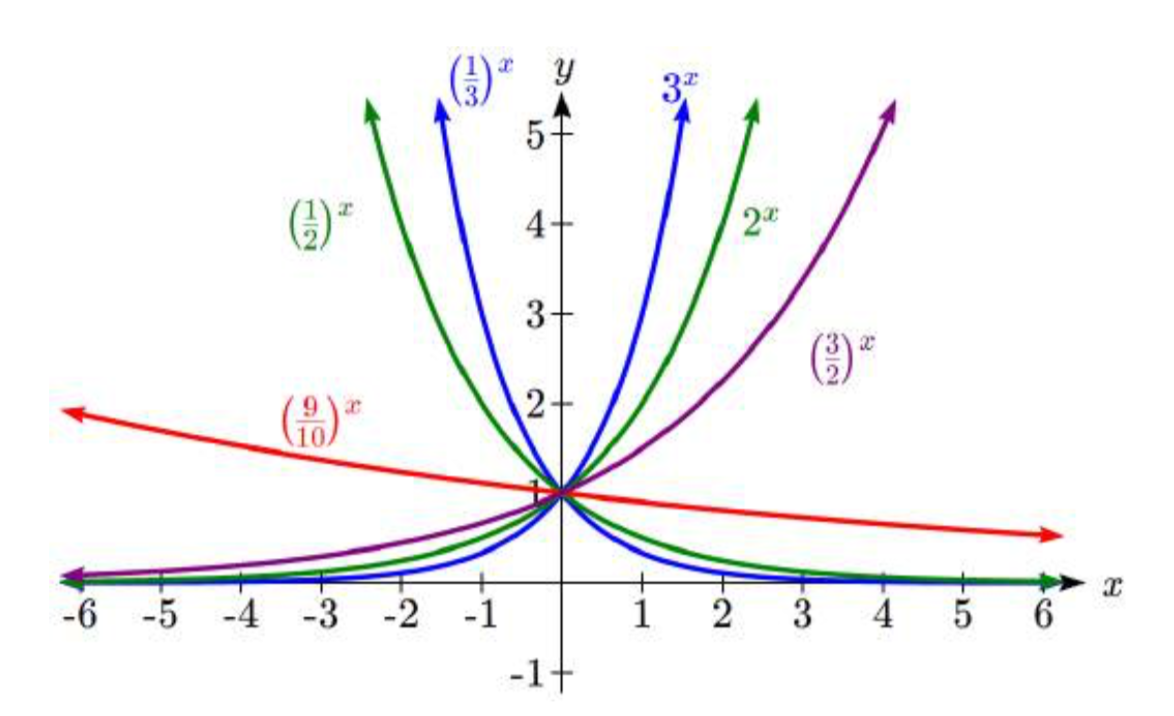
$Una gráfica que muestra seis gráficas exponenciales en los mismos ejes. Todos pasan por el eje y en 1. Tres gráficas están disminuyendo: nueve décimas a la x es la más plana. la mitad a la x comienza más empinada. un tercio a la x comienza la más empinada de las tres pero también se nivela hacia el eje x a la derecha más rápidamente. Tres gráficas van en aumento: tres mitades a la x es la más plana, seguida de 2 a la x. 3 a la x se mantiene más plana a la izquierda durante más tiempo, pero luego se vuelve más empinada más rápido cuando x se vuelve positiva.$

Observe que cuanto más cerca$b$ esté el valor de 1, menos empinada será la gráfica.

En el siguiente conjunto de gráficas, a se altera y nuestro valor para$b$ sigue siendo el mismo.

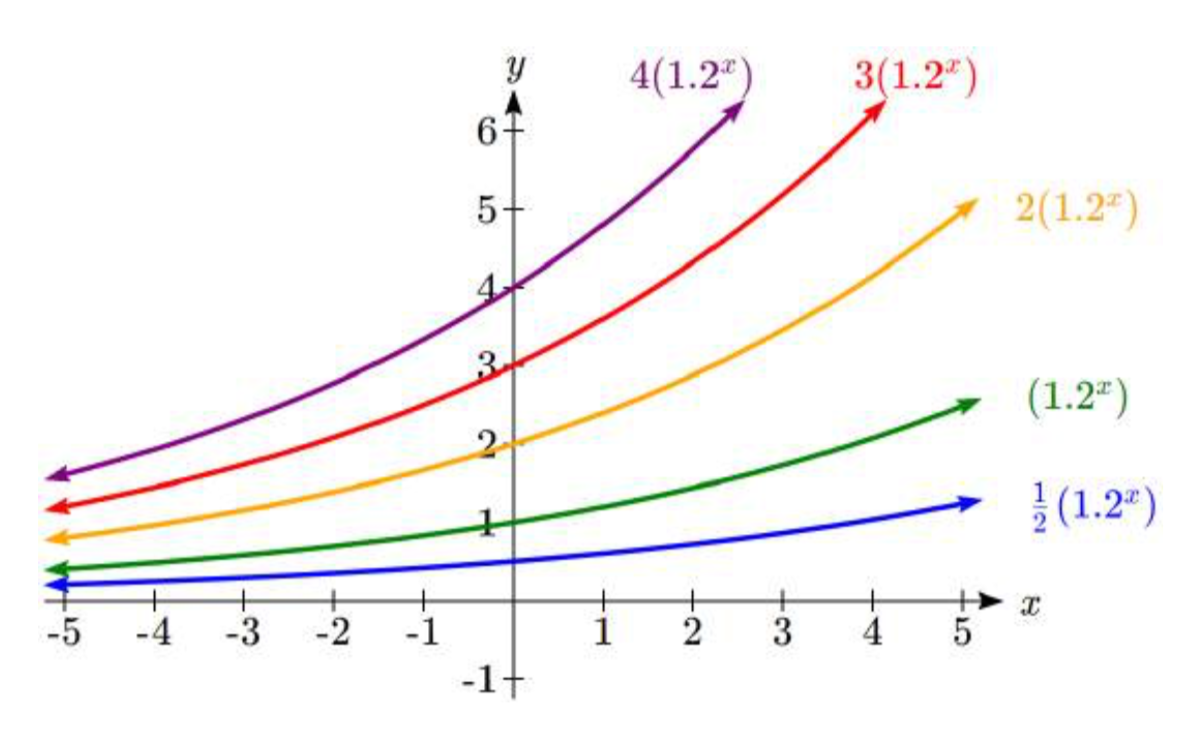
$Una gráfica que muestra cinco gráficas exponenciales en los mismos ejes. Todos son múltiplos de 1.2 a la x. una mitad veces 1.2 a la x cruza el eje y a la mitad, y aumenta más lentamente, seguido de 1.2 a la x, luego 2 veces 1.2 a la x, y 3 veces 1.2 a la x y 4 veces 1.2 a la x. A medida que el múltiplo aumenta, la intercepción y cambia, y la gráfica aumenta algo más rápido.$

Observe que cambiando el valor para$a$ cambia la intercepción vertical. Dado que a está multiplicando el${b}^{x}$ término, a actúa como factor de estiramiento vertical, no como un desplazamiento. Observe también que el comportamiento a largo plazo para todas estas funciones es el mismo porque el factor de crecimiento no cambió y ninguno de estos a valores introdujo un giro vertical.

Ejemplo$\PageIndex{2}$

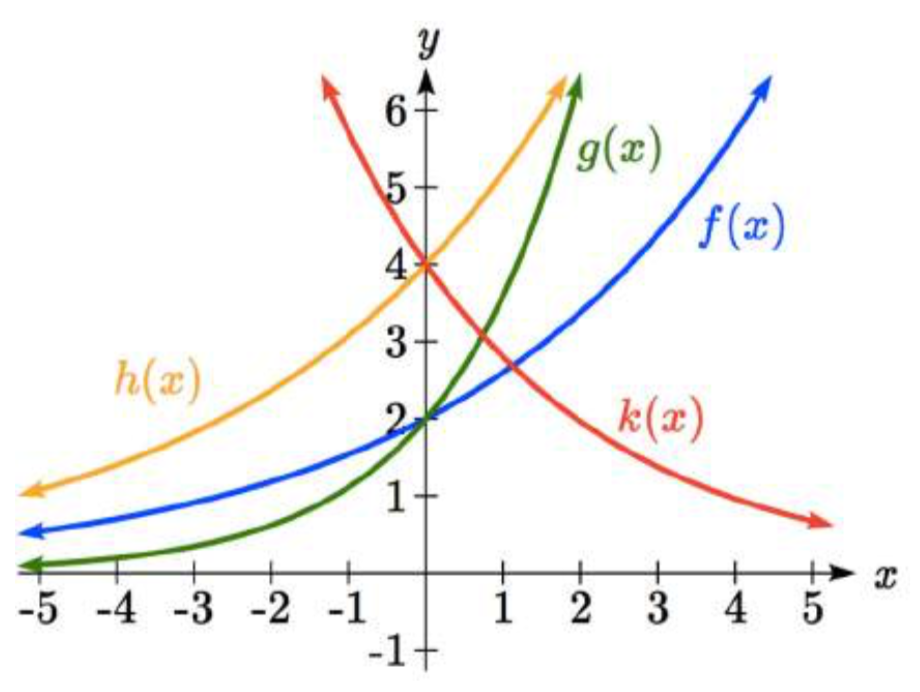
Coincidir cada ecuación con su gráfica. 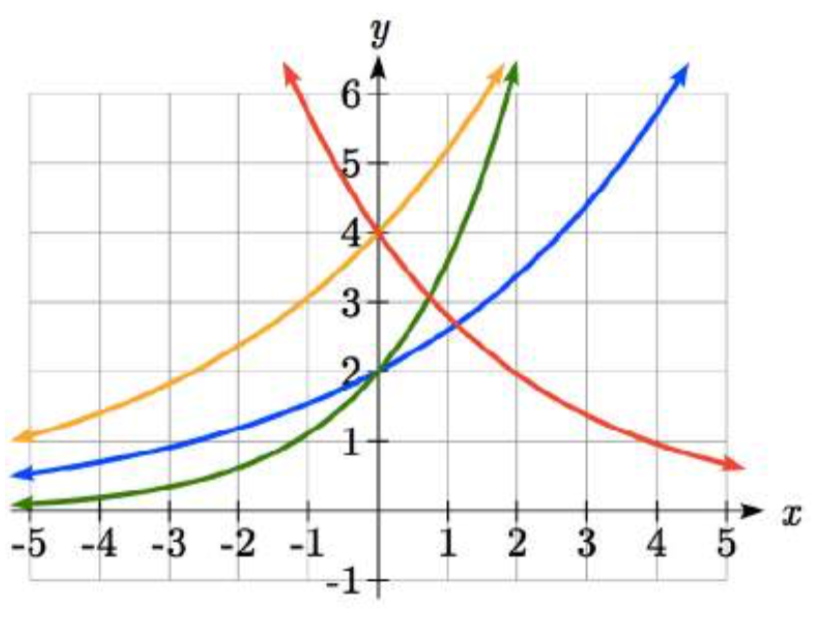$Una gráfica que muestra cuatro curvas exponenciales en los mismos ejes. El primero, en amarillo, va en aumento y pasa el eje y en 4. El segundo, en azul, va aumentando lentamente y pasa el eje y en 2. El tercero, en verde, también está aumentando y pasa el eje y en 2, pero se curva hacia arriba más rápidamente que la segunda gráfica. El cuarto, en rojo, es decreciente y pasa el eje y en 4.$

\[{f(x)=2(1.3)^{x} }\nonumber\]

\[{g(x)=2(1.8)^{x} }\nonumber \]

\[{h(x)=4(1.3)^{x} }\nonumber \]

\[{k(x)=4(0.7)^{x} }\nonumber\]

Solución

La gráfica de$k(x)$ es la más fácil de identificar, ya que es la única ecuación con un factor de crecimiento menor a uno, lo que producirá una gráfica decreciente. La gráfica de se$h(x)$ puede identificar como la única función exponencial creciente con una intercepción vertical en (0,4). Las gráficas de$f(x)$ y$g(x)$ ambas tienen una intercepción vertical en (0,2), pero como$g(x)$ tiene un factor de crecimiento mayor, podemos identificarla como la gráfica que aumenta más rápido.

$Una gráfica que muestra cuatro curvas exponenciales en los mismos ejes. El primero, en amarillo, etiquetado h de x, va en aumento y pasa el eje y en 4. El segundo, en azul, etiquetado f de x, va aumentando lentamente y pasa el eje y en 2. El tercero, en verde, etiquetado como g de x, también está aumentando y pasa el eje y en 2, pero se curva hacia arriba más rápidamente que la segunda gráfica. El cuarto, en rojo, etiquetado k de x, es decreciente y pasa el eje y en 4.$

Ejercicio$\PageIndex{1}$

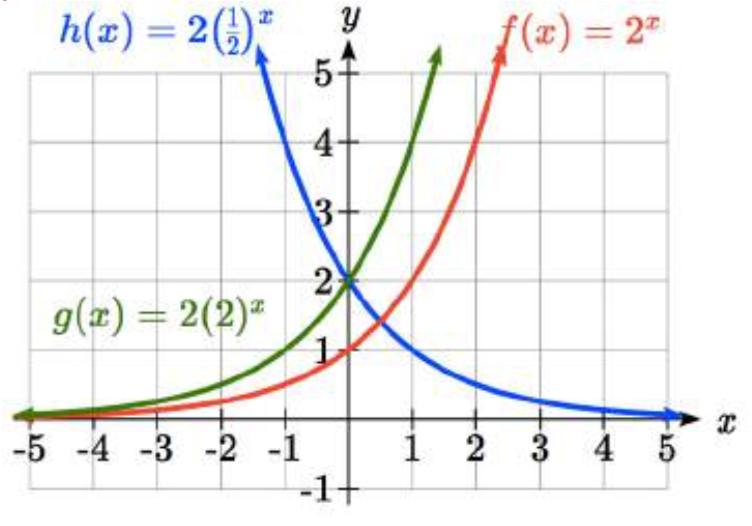
Grafique las siguientes funciones en el mismo eje:

$f(x)=(2)^{x}$;$g(x)=2(2)^{x}$;$h(x)=2(1/2)^{x}$.

Responder: $Tres gráficas sobre los mismos ejes. Primero, una gráfica exponencial creciente que pasa por 0 coma 1 y 1 coma 2 etiquetada f de x = 2 a la x. Segundo, una gráfica exponencial creciente que pasa por 0 coma 2 y 2 coma 4 etiquetada g de x = 2 veces 2 a la x. Tercero, una gráfica exponencial decreciente que pasa por negativos 1 coma 4 y 0 coma 2 etiquetada h de x = 2 veces la mitad a la x.$

Transformaciones de Gráficas Exponenciales

Funciones Exponenciales: Transformaciones de Gráficas Exponenciales

Si bien las funciones exponenciales se pueden transformar siguiendo las mismas reglas que cualquier función, hay algunas características interesantes de las transformaciones que se pueden identificar. El primero se vio al inicio de la sección —que una reflexión horizontal equivale a un cambio en el factor de crecimiento. Así mismo, dado que$a$ es en sí mismo un factor de estiramiento, un estiramiento vertical de un exponencial se corresponde con un cambio en el valor inicial de la función.

A continuación, considere el efecto de un desplazamiento horizontal sobre una función exponencial. Desplazar la función$f(x)=3(2)^{x}$ cuatro unidades hacia la izquierda daría$f(x+4)=3(2)^{x+4}$. Empleando reglas de exponente, podríamos reescribir esto:

\[f(x+4)=3(2)^{x+4} =3(2)^{x} (2^{4} )=48(2)^{x}\nonumber\]

Curiosamente, resulta que un desplazamiento horizontal de una función exponencial se corresponde con un cambio en el valor inicial de la función.

Por último, considerar el efecto de un desplazamiento vertical sobre una función exponencial. $f(x)=3(2)^{x}$Bajar 4 unidades daría la ecuación$f(x)=3(2)^{x} -4$.

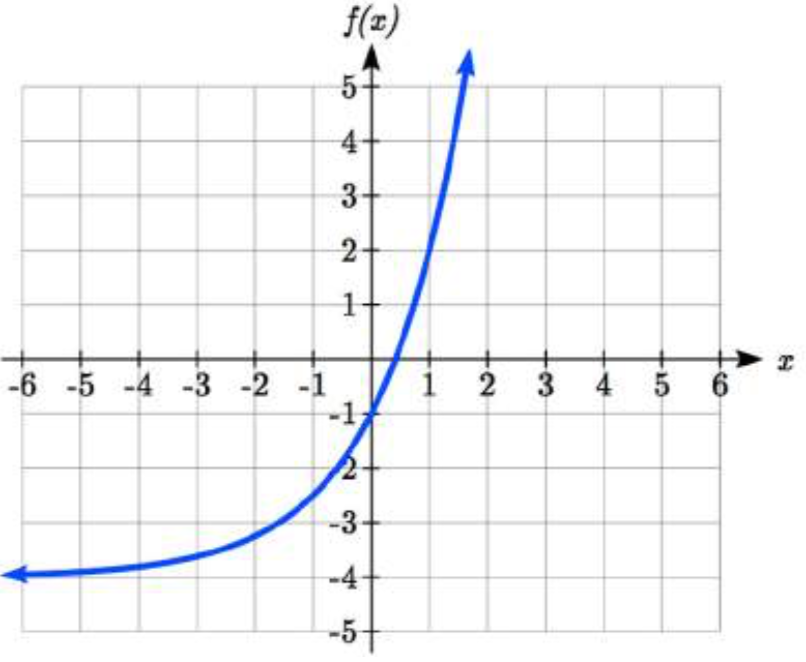$Un gráfico que comienza plano, justo por encima de y=negativo 4, y aumenta y curva hacia arriba, pasando por el eje y en negativo 1 y el punto 1 coma 2$ Graficando eso, observe que es sustancialmente diferente a la gráfica exponencial básica. A diferencia de un exponencial básico, esta gráfica no tiene una asíntota horizontal en$y = 0$; debido al desplazamiento vertical, la asíntota horizontal también se ha desplazado a$y = -4$. Podemos ver eso como$x \to \infty$,$f(x) \to \infty$ y como$x \to -\infty$,$f(x) \to -4$.

Hemos determinado que un desplazamiento vertical es la única transformación de una función exponencial que cambia la gráfica de una manera que no se puede lograr alterando los parámetros$a$ y$b$ en la función exponencial básica$f(x)=ab^{x}$.

transformaciones de exponenciales

Cualquier exponencial transformado se puede escribir en la forma

\[f(x)=ab^{x} +c\nonumber\]

donde$y = c$ está la asíntota horizontal.

Tenga en cuenta que, debido al desplazamiento, la intercepción vertical se desplaza a (0,$a+c$).

Ejercicio$\PageIndex{2}$

Escribe la ecuación y grafica la función exponencial descrita de la siguiente manera:$f(x)=e^{x}$ se estira verticalmente por un factor de 2, se voltea a través del eje y y se desplaza hacia arriba 4 unidades.

Responder

\[f(x)=-2e^{x} +4\nonumber\]

$Una gráfica que comienza casi plana, justo por debajo de y=4, que disminuye curvándose hacia abajo pasando por 0 coma 2$

Ejemplo$\PageIndex{3}$

Dibuje una gráfica de$f(x)=-3\left(\dfrac{1}{2} \right)^{x} +4$.

Solución

Observe que en esta función exponencial, el negativo en el factor de estiramiento -3 provocará una reflexión vertical, y el desplazamiento vertical hacia arriba 4 moverá la asíntota horizontal a$y$ = 4. Dibujando esto como una transformación de$g(x)=\left(\dfrac{1}{2} \right)^{x}$,

El básico$g(x) = (\dfrac{1}{2})^x$ Verticalmente Reflejado y Estirado por 3 Desplazado verticalmente hacia arriba

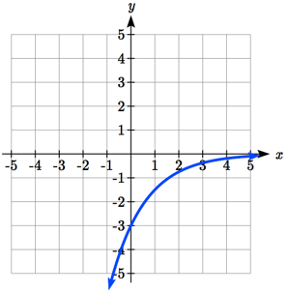
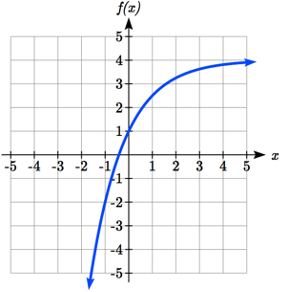
$Una gráfica que comienza disminuyendo rápidamente y se aplana a medida que x aumenta, pasando por negativo 1 coma 2 y 0 coma 1, nivelándose hacia el eje y a medida que x se agranda$ $Una gráfica que comienza negativa y aumenta rápidamente, aplanándose a medida que x aumenta, pasando por 0 coma negativa 3, nivelándose hacia el eje y a medida que x se agranda$ $Una gráfica que comienza negativa y aumenta rápidamente, aplanándose a medida que x aumenta, pasando por 0 coma 1, nivelándose hacia y=4 a medida que x se agranda$

Observe que mientras el dominio de esta función no se modifica, debido a la reflexión y desplazamiento, el rango de esta función lo es$\left(-\infty ,4\right)$.

Como$x \to \infty$,$f(x) \to 4$ y como$x \to -\infty$,$f(x) \to -\infty$.

Las funciones que conducen a gráficas como la anterior son comunes como modelos de aprendizaje y modelos de crecimiento acercándose a un límite.

Ejemplo$\PageIndex{4}$

Encuentra una ecuación para la función graficada.

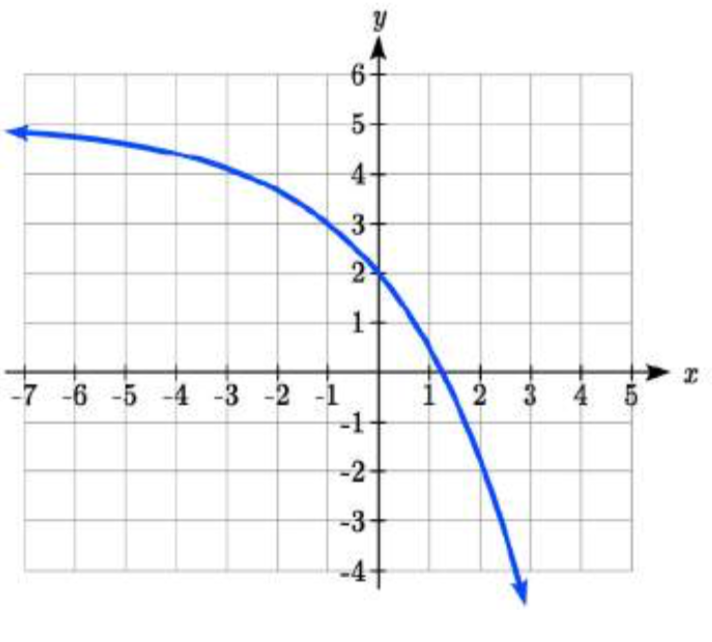
$Una gráfica que comienza casi plana, justo por debajo de y=5, que disminuye, curvándose hacia abajo, pasando por negativo 1 coma 3 y 0 coma 2$

Solución

Al mirar esta gráfica, parece tener una asíntota horizontal$y = 5$, sugiriendo una ecuación de la forma$f(x)=ab^{x} +5$. Para encontrar valores para$a$ y$b$, podemos identificar otros dos puntos en la gráfica. Parece que la gráfica pasa por (0,2) y (-1,3), por lo que podemos usar esos puntos. Sustituir en (0,2) nos permite resolver para$a$.

\[\begin{array}{l} {2=ab^{0} +5} \\ {2=a+5} \\ {a=-3} \end{array}\nonumber\]

Sustituir en (-1,3) nos permite resolver para$b$

\[\begin{array}{l} {3=-3b^{-1} +5} \\ {-2=\dfrac{-3}{b} } \\ {-2b=-3} \\ {b=\dfrac{3}{2} =1.5} \end{array}\nonumber\]

La fórmula final para nuestra función es$f(x)=-3(1.5)^{x} +5$.

Ejercicio$\PageIndex{3}$

Dada la gráfica de la función exponencial transformada, encontrar una fórmula y describir el comportamiento a largo plazo.

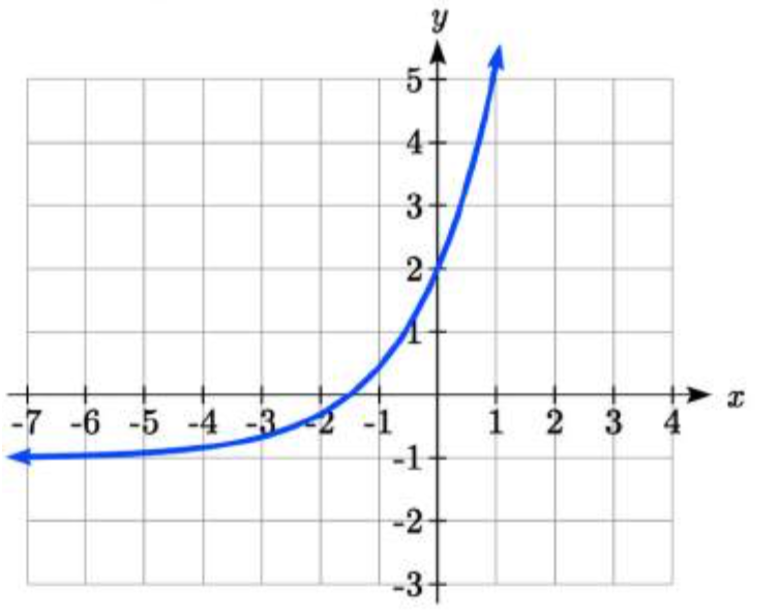
$Una gráfica que comienza casi plana, justo por encima de y=negativo 1, que aumenta curvándose hacia arriba, pasando por 0 coma 2$

Responder

Asíntota horizontal a$y$ = -1, entonces$f(x)=ab^{x} -1$.

Sustituir (0, 2) para encontrar$a$ = 3.Sustituir (1,5) para encontrar$5=3b^{1} -1$,$b$ = 2.

\[f(x)=3(2^{x} )-1\text{ or }f(x)=3(.5)^{-x} -1\nonumber\]

Como$x \to \infty$,$f(x) \to \infty$ y como$x \to -\infty$,$f(x) \to -1$

Temas Importantes de esta Sección

Gráficas de funciones exponenciales
Interceptar
Factor de crecimiento
Crecimiento Exponencial
Decaimiento exponencial
Intercepciones horizontales
Comportamiento a largo plazo
Transformaciones

\(x\)	-3	-2	-1	0	1	2	3
\(f(x)\)	\(\dfrac{1}{8}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{2}\)	1	2	4	8

\(x\)	-3	-2	-1	0	1	2	3
\(g(x)\)	8	4	2	1	\(\dfrac{1}{2}\)	\(\dfrac{1}{4}\)	\(\dfrac{1}{8}\)