4.6: Modelos Exponenciales y Logarítmicos
- Page ID
- 116891
Si bien hemos explorado algunas aplicaciones básicas de funciones exponenciales y logarítmicas, en esta sección exploramos algunas aplicaciones importantes con más profundidad.
Desintegración radiactiva
En una sección anterior, discutimos la desintegración radiactiva, la idea de que los isótopos radiactivos cambian con el tiempo. Uno de los términos comunes asociados con la desintegración radiactiva es la vida media.
Definición: Half Life
La vida media de un isótopo radiactivo es el tiempo que tarda la mitad de la sustancia en descomponerse.
Dada la ecuación básica de crecimiento/decaimiento exponencial\(h(t)=ab^{t}\), la vida media se puede encontrar resolviendo para cuando queda la mitad de la cantidad original; resolviendo\(\dfrac{1}{2} a=a(b)^{t}\), o más simplemente\(\dfrac{1}{2} =b^{t}\). Observe cómo la cantidad inicial es irrelevante a la hora de resolver para la vida media.
Ejemplo\(\PageIndex{1}\)
El bismuto-210 es un isótopo que decae aproximadamente 13% cada día. ¿Cuál es la vida media del Bismuth-210?
Solución
No nos dieron una cantidad inicial, así que podíamos compensar un valor o usar una constante desconocida para representar la cantidad inicial. Para demostrar que la cantidad inicial no afecta el resultado, denotemos la cantidad inicial por la constante a. Entonces la descomposición del bismuto-210 puede ser descrita por la ecuación\(Q(d)=a(0.87)^{d}\).
Para encontrar la vida media, queremos determinar cuándo la cantidad restante es la mitad de la original:\(\dfrac{1}{2} a\). Resolviendo,
\[\dfrac{1}{2} a=a(0.87)^{d}\nonumber\]Dividir por\(a\),
\[\dfrac{1}{2} =0.87^{d}\nonumber\]Tome el tronco de ambos lados
\[\log \left(\dfrac{1}{2} \right)=\log \left(0.87^{d} \right)\nonumber\]Usar la propiedad exponente de los registros
\[\log \left(\dfrac{1}{2} \right)=d\log \left(0.87\right)\nonumber\]Dividir para resolver\(d\)
\[d=\dfrac{\log \left(\dfrac{1}{2} \right)}{\log \left(0.87\right)} \approx 4.977\text{ days}\nonumber \]
Esto nos dice que la vida media del bismuto-210 es de aproximadamente 5 días.
Ejemplo\(\PageIndex{2}\)
El cesio-137 tiene una vida media de aproximadamente 30 años. Si comienzas con 200 mg de cesio-137, ¿cuánto quedará después de 30 años? ¿60 años? ¿90 años?
Solución
Dado que la vida media es de 30 años, después de 30 años, quedará la mitad de la cantidad original, 100 mg.
Después de 60 años, han pasado otros 30 años, por lo que durante esos segundos 30 años, otra mitad de la sustancia se desintegrará, dejando 50 mg.
Después de 90 años, han pasado otros 30 años, por lo que otra mitad de la sustancia se desintegrará, dejando 25 mg.
Ejemplo\(\PageIndex{3}\)
El cesio-137 tiene una vida media de aproximadamente 30 años. Encuentra la tasa de decaimiento anual.
Solución
Ya que estamos buscando una tasa de decaimiento anual, utilizaremos una ecuación de la forma\(Q(t)=a(1+r)^{t}\). Sabemos que después de 30 años quedará la mitad del monto original. Uso de esta información
\[\dfrac{1}{2} a=a(1+r)^{30}\nonumber\]Dividiendo por\(a\)
\[\dfrac{1}{2} =(1+r)^{30}\nonumber\]Tomando la\({}^{th}\) raíz 30 de ambos lados
\[\sqrt[{30}]{\dfrac{1}{2} } =1+r\nonumber\]restando uno de ambos lados,
\[r=\sqrt[{30}]{\dfrac{1}{2} } -1\approx -0.02284\nonumber\]
Esto nos dice que el cesio-137 está en descomposición a una tasa anual de 2.284% anual.
Ejercicio\(\PageIndex{1}\)
El cloro-36 se elimina del organismo con una vida media biológica de 10 días (www.ead.anl.gov/pub/doc/chlorine.pdf). Encuentra la tasa de decaimiento diario.
- Contestar
-
\(r = \sqrt[10]{\dfrac{1}{2}} - 1 \approx -0.067\)o 6.7% es la tasa diaria de decaimiento.
Ejemplo\(\PageIndex{4}\)
El carbono-14 es un isótopo radiactivo que está presente en materiales orgánicos., y se usa comúnmente para fechar artefactos históricos. El carbono-14 tiene una vida media de 5730 años. Si se encuentra un fragmento de hueso que contiene 20% de su carbono-14 original, ¿qué edad tiene el hueso?
Solución
Para saber qué edad tiene el hueso, primero necesitaremos encontrar una ecuación para la descomposición del carbono-14. Podríamos usar una fórmula de decaimiento continuo o anual, pero optar por usar la fórmula de decaimiento continuo ya que es más común en los textos científicos. La vida media nos dice que después de 5730 años, queda la mitad de la sustancia original. Resolviendo para la tasa,
\[\dfrac{1}{2} a=ae^{r5730}\nonumber\]Dividiendo por\(a\)
\[\dfrac{1}{2} =e^{r5730}\nonumber\]Tomando el tronco natural de ambos lados
\[\ln \left(\dfrac{1}{2} \right)=\ln \left(e^{r5730} \right)\nonumber\]Utilice la propiedad inversa de los registros en el lado derecho
\[\ln \left(\dfrac{1}{2} \right)=5730r\nonumber\]Dividir por 5730
\[r=\dfrac{\ln \left(\dfrac{1}{2} \right)}{5730} \approx -0.000121\nonumber\]
Ahora sabemos que la decadencia seguirá la ecuación\(Q(t)=ae^{-0.000121t}\). Para encontrar la antigüedad del fragmento de hueso que contiene 20% de la cantidad original, resolvemos para\(t\) eso\(Q(t) = 0.20a\).
\[0.20a=ae^{-0.000121t}\nonumber\]
\[0.20=e^{-0.000121t}\nonumber\]
\[\ln (0.20)=\ln \left(e^{-0.000121t} \right)\nonumber\]
\[\ln (0.20)=-0.000121t\nonumber\]
\[t=\dfrac{\ln (0.20)}{-0.000121} \approx 13301\text{ years}\nonumber\]
El fragmento óseo tiene aproximadamente 13.300 años de edad.
Ejercicio\(\PageIndex{2}\)
En el Ejemplo 2, aprendimos que el Cesio-137 tiene una vida media de aproximadamente 30 años. Si comienzas con 200 mg de cesio-137, ¿tardará más o menos de 230 años hasta que solo quede 1 miligramo?
- Contestar
-
Menos de 230 años, 229.3157 para ser exactos.
Tiempo de Duplicación
Para las cantidades en descomposición, preguntamos cuánto tiempo tarda la mitad de la sustancia en descomponerse. Para cantidades crecientes podríamos preguntar cuánto tiempo tarda en duplicarse la cantidad.
Definición: Tiempo de duplicación
El tiempo de duplicación de una cantidad creciente es el tiempo que tarda en duplicarse la cantidad.
Dada la ecuación básica de crecimiento exponencial\(h(t)=ab^{t}\), el tiempo de duplicación se puede encontrar resolviendo para cuando la cantidad original se haya duplicado; resolviendo\(2a=a(b)^{x}\), o más simplemente\(2=b^{x}\). Al igual que con la decadencia, la cantidad inicial es irrelevante a la hora de resolver el tiempo de duplicación.
Ejemplo\(\PageIndex{5}\)
Las células cancerosas a veces aumentan exponencialmente. Si un crecimiento canceroso contenía 300 células el mes pasado y 360 células este mes, ¿cuánto tiempo tardará en duplicarse el número de células cancerosas?
Solución
Definiendo\(t\) ser tiempo en meses, con\(t = 0\) correspondiente a este mes, se nos dan dos piezas de datos: este mes, (0, 360), y el mes pasado, (-1, 300).
A partir de estos datos, podemos encontrar una ecuación para el crecimiento. Usando el formulario\(C(t)=ab^{t}\), conocemos inmediatamente a = 360, dando\(C(t)=360b^{t}\). Sustituyendo en (-1, 300),\[\begin{array}{l} {300=360b^{-1} } \\ {300=\dfrac{360}{b} } \\ {b=\dfrac{360}{300} =1.2} \end{array}\nonumber\]
Esto nos da la ecuación\(C(t)=360(1.2)^{t}\)
Para encontrar el tiempo de duplicación, buscamos el momento en el que tendremos el doble de la cantidad original, así que cuándo\(C(t) = 2a\).
\[2a=a(1.2)^{t}\nonumber\]
\[2=(1.2)^{t}\nonumber\]
\[\log \left(2\right)=\log \left(1.2^{t} \right)\nonumber\]
\[\log \left(2\right)=t\log \left(1.2\right)\nonumber\]
\[t=\dfrac{\log \left(2\right)}{\log \left(1.2\right)} \approx 3.802\nonumber\]meses para que el número de células cancerosas se duplique.
Ejemplo\(\PageIndex{6}\)
El uso de un nuevo sitio web de redes sociales ha ido creciendo exponencialmente, con el número de nuevos miembros duplicándose cada 5 meses. Si el sitio actualmente cuenta con 120,000 usuarios y esta tendencia continúa, ¿cuántos usuarios tendrá el sitio en 1 año?
Solución
Podemos usar el tiempo de duplicación para encontrar una función que modele el número de usuarios del sitio, y luego usar esa ecuación para responder a la pregunta. Si bien podríamos usar una a arbitraria como tenemos antes para la cantidad inicial, en este caso, sabemos que la cantidad inicial fue de 120,000.
Si usamos una ecuación de crecimiento continuo, se vería así\(N(t)=120e^{rt}\), medida en miles de usuarios después de t meses. Con base en el tiempo de duplicación, habría 240 mil usuarios después de 5 meses. Esto nos permite resolver para la tasa de crecimiento continuo:
\[240=120e^{r5}\nonumber\]
\[2=e^{r5}\nonumber\]
\[\ln 2=5r\nonumber\]
\[r=\dfrac{\ln 2}{5} \approx 0.1386\nonumber\]
Ahora que tenemos una ecuación,\(N(t)=120e^{0.1386t}\), podemos predecir el número de usuarios después de 12 meses:
\[N(12) =120e^{0.1386(12)} =633.140\text{ thousand users}\nonumber\].
Entonces después de 1 año, esperaríamos que el sitio tuviera alrededor de 633.140 usuarios.
Ejercicio\(\PageIndex{3}\)
Si la matrícula en una universidad aumenta 6.6% cada año, ¿cuántos años tardará en duplicarse la matrícula?
- Contestar
-
Resolviendo\(a (1 + 0.066)^t = 2a\), tomará\(t = \dfrac{log(2)}{log(1.066)} \approx 10.845\) años, o aproximadamente 11 años, para que la colegiatura se duplique.
Ley de Refrigeración de Newton
Cuando un objeto caliente se deja en el aire circundante que está a una temperatura más baja, la temperatura del objeto disminuirá exponencialmente, nivelándose hacia la temperatura del aire circundante. Esta “nivelación” corresponderá a una asíntota horizontal en la gráfica de la función de temperatura. A menos que la temperatura ambiente sea cero, esto corresponderá a un desplazamiento vertical de la función genérica de decaimiento exponencial.
Definición: Ley del Enfriamiento de Newton
La temperatura de un objeto,\(T\), en el aire circundante con la temperatura\(T_{s}\) se comportará de acuerdo con la fórmula
\[T(t)=ae^{kt} +T_{s}\]
Dónde
- \(t\)es tiempo
- \(a\)es una constante determinada por la temperatura inicial del objeto
- \(k\)es una constante, la tasa continua de enfriamiento del objeto
Si bien se\(T(t)=ab^{t} +T_{s}\) podría utilizar una ecuación de la forma, la forma de crecimiento continuo es más común.
Ejemplo\(\PageIndex{7}\)
Una tarta de queso se saca del horno con una temperatura interna ideal de 165 grados Fahrenheit, y se coloca en un refrigerador de 35 grados. Después de 10 minutos, la tarta de queso se ha enfriado a 150 grados. Si debes esperar hasta que la tarta de queso se haya enfriado a 70 grados antes de comerla, ¿cuánto tiempo tendrás que esperar?
Solución
Dado que la temperatura del aire circundante en el refrigerador es de 35 grados, la temperatura de la tarta de queso disminuirá exponencialmente hacia 35, siguiendo la ecuación
\[T(t)=ae^{kt} +35\nonumber\]
Sabemos que la temperatura inicial era de 165, entonces\(T(0)=165\). Sustituyendo en estos valores,
\[\begin{array}{l} {165=ae^{k0} +35} \\ {165=a+35} \\ {a=130} \end{array}\nonumber\]
Nos dieron otro par de datos\(T(10)=150\), que podemos usar para resolver\(k\)
\[150=130e^{k10} +35\nonumber\]
\[\begin{array}{l} {115=130e^{k10} } \\ {\dfrac{115}{130} =e^{10k} } \\ {\ln \left(\dfrac{115}{130} \right)=10k} \\ {k=\dfrac{\ln \left(\dfrac{115}{130} \right)}{10} =-0.0123} \end{array}\nonumber\]
Juntos esto nos da la ecuación para el enfriamiento:\[T(t)=130e^{-0.0123t} +35\nonumber\]
Ahora podemos resolver por el tiempo que tardará en que la temperatura se enfríe a 70 grados.
\[70=130e^{-0.0123t} +35\nonumber\]
\[35=130e^{-0.0123t}\nonumber\]
\[\dfrac{35}{130} =e^{-0.0123t}\nonumber\]
\[\ln \left(\dfrac{35}{130} \right)=-0.0123t\nonumber\]
\[t=\dfrac{\ln \left(\dfrac{35}{130} \right)}{-0.0123} \approx 106.68\nonumber\]
Tardará unos 107 minutos, o una hora y 47 minutos, para que la tarta de queso se enfríe. Por supuesto, si te gusta tu tarta de queso servida fría, tendrías que esperar un poco más.
Ejercicio\(\PageIndex{4}\)
Una jarra de agua a 40 grados Fahrenheit se coloca en una habitación de 70 grados. Una hora después la temperatura ha subido a 45 grados. ¿Cuánto tiempo tardará en subir la temperatura a 60 grados?
- Contestar
-
\(T(t) = ae^{kt} + 70\). Sustituyendo (0, 40), encontramos\(a = -30\). Sustituyendo (1, 45), resolvemos\[45 = -30 e^{k(1)} + 70\nonumber\] para obtener\[k = ln(\dfrac{25}{30}) = -0.1823\nonumber\]
Resolver\(60 = -30e^{-0.1823t} + 70\) da
\[t = \dfrac{ln(1/3)}{-0.1823} = 6.026\text{ hours}\nonumber \]
Escalas logarítmicas
Para cantidades que varían mucho en magnitud, una escala estándar de medición no siempre es efectiva, y la utilización de logaritmos puede hacer que los valores sean más manejables. Por ejemplo, si se listan las distancias promedio desde el sol hasta los cuerpos principales de nuestro sistema solar, ves que varían mucho.
| Planeta | Distancia (millones de km) |
| Mercurio | 58 |
| Venus | 108 |
| Tierra | 150 |
| Marte | 228 |
| Júpiter | 779 |
| Saturno | 1430 |
| Urano | 2880 |
| Neptuno | 4500 |
Colocado en una escala lineal, una con valores igualmente espaciados, estos valores se agrupan.

0 500 1000 1500 2000 2500 3000 3500 4000 4500
Sin embargo, calcular el logaritmo de cada valor y trazar estos nuevos valores en una recta numérica da como resultado una gráfica más manejable, y hace que las distancias relativas sean más aparentes. (Es interesante notar la gran brecha entre Marte y Júpiter en la línea del número de registro. Allí se encuentra el cinturón de asteroides, que los científicos creen que es un planeta que nunca se formó por los efectos de la gravedad de Júpiter).
| Planeta | Distancia (millones de km) | registro (distancia) |
| Mercurio | 58 | 1.76 |
| Venus | 108 | 2.03 |
| Tierra | 150 | 2.18 |
| Marte | 228 | 2.36 |
| Júpiter | 779 | 2.89 |
| Saturno | 1430 | 3.16 |
| Urano | 2880 | 3.46 |
| Neptuno | 4500 | 3.65 |
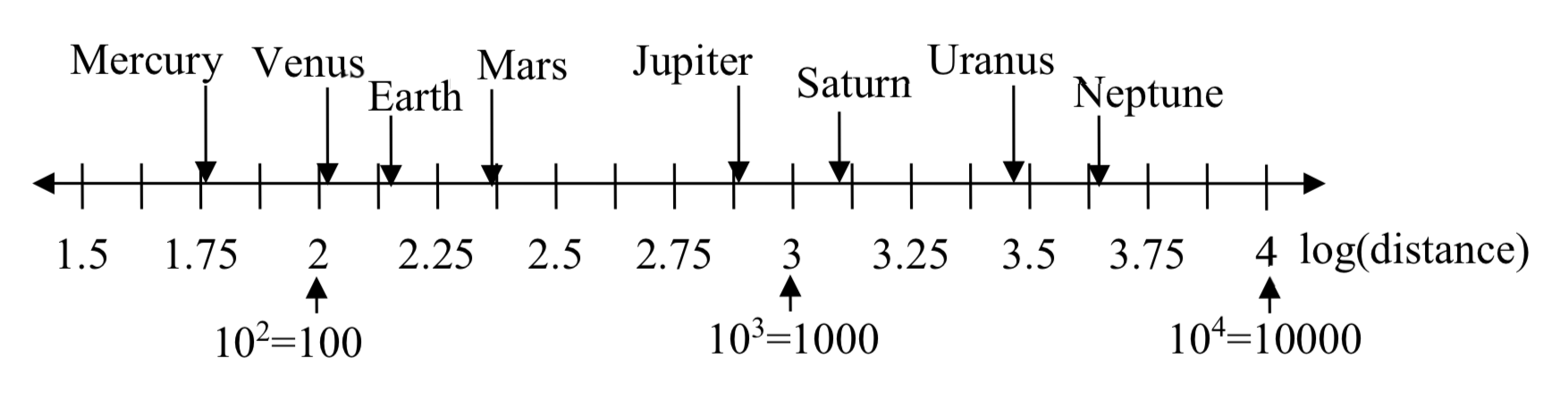
En ocasiones, como se muestra arriba, la escala en una línea numérica logarítmica mostrará los valores logarítmicos, pero más comúnmente los valores originales se listan como potencias de 10, como se muestra a continuación.

Ejemplo\(\PageIndex{8}\)
Estimar el valor del punto\(P\) en la escala logarítmica anterior
El punto\(P\) parece estar a medio camino entre -2 y -1 en valor logarítmico, por lo que si\(V\) es el valor de este punto,
\[\log (V)\approx -1.5\nonumber\]Reescritura en forma exponencial,
\[V\approx 10^{-1.5} =0.0316\nonumber\]
Ejemplo\(\PageIndex{9}\)
Colocar el número 6000 en una escala logarítmica.
Solución
Ya que\(\log (6000)\approx 3.8\), este punto pertenecería en la escala logarítmica por aquí:

Ejercicio\(\PageIndex{5}\)
Trazar los datos de la siguiente tabla en una escala logarítmica (De http://www.epd.gov.hk/epd/noise_educ...1/intro_5.html, recuperado el 2 de octubre de 2010).
| Fuente de sonido/ruido | Presión sonora aproximada en\(\mu\) Pa (micro Pascales) |
| Lanzamiento del transbordador espacial | 2000,000,000 |
| Orquesta Sinfónica Completa | 2000,000 |
| Tren de Carga Diesel a Alta Velocidad a 25 m | 200,000 |
| Conversación Normal | 20,000 |
| Suave susurro a 2 m en Biblioteca | 2,000 |
| Estudio de transmisión desocupado | 200 |
| El sonido más suave que un humano puede escuchar | 20 |
- Contestar
-
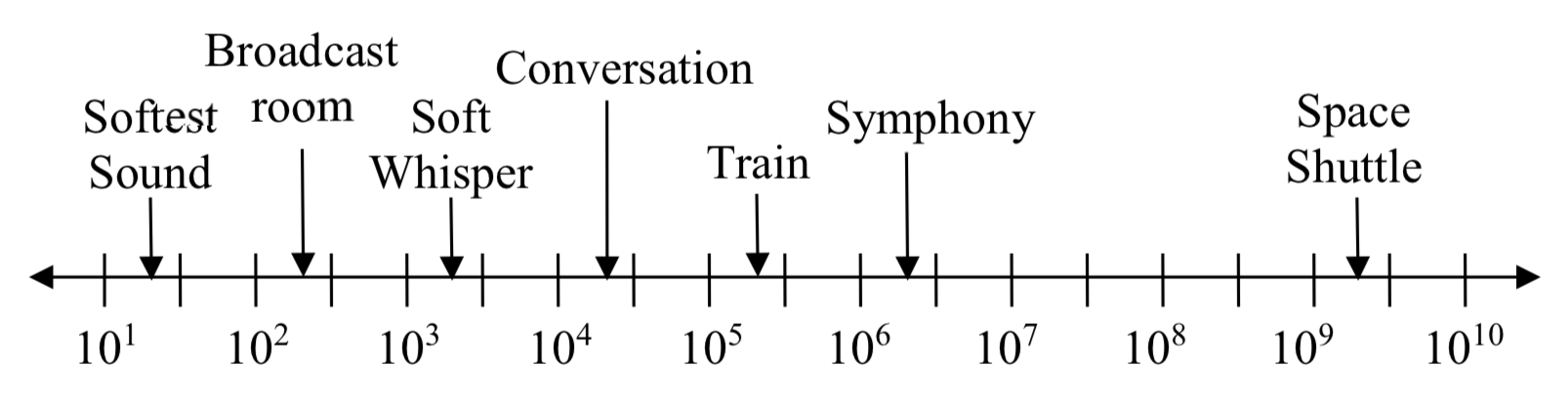
Observe que en la escala logarítmica superior al Ejemplo 8, la distancia visual en la escala entre puntos\(A\)\(B\) y\(C\) y entre y\(D\) es la misma. Al mirar los valores a los que corresponden estos puntos, el aviso\(B\) es diez veces el valor de\(A\), y\(D\) es diez veces el valor de\(C\). Una\(linear\) diferencia visual entre puntos corresponde a un cambio relativo (ratio) entre los valores correspondientes.
Los logaritmos son útiles para mostrar estos cambios relativos. Por ejemplo, al comparar $1,000,000 a $10,000, el primero es 100 veces mayor que el segundo.
\[\dfrac{1,000,000}{10,000} = 100 = 10^2\nonumber\]
De igual manera, comparando $1000 a $10, el primero es 100 veces mayor que el segundo.
\[\dfrac{1,000}{10} = 100 = 10^2\nonumber\]
Cuando una cantidad es aproximadamente diez veces mayor que otra, decimos que es un orden de magnitud mayor. En ambos casos descritos anteriormente, el primer número fue dos órdenes de magnitud mayor que el segundo.
Observe que el orden de magnitud se puede encontrar como el logaritmo común de la relación de las cantidades. En la escala logarítmica anterior, B es un orden de magnitud mayor que\(A\), y\(D\) es un orden de magnitud mayor que\(C\).
Definición: Órdenes de magnitud
Dados dos valores\(A\) y\(B\), para determinar cuántos órdenes de magnitud\(A\) es mayor que\(B\),
Diferencia en órdenes de magnitud = log (\(\dfrac{A}{B})\)
Ejemplo\(\PageIndex{10}\)
En la escala logarítmica anterior al Ejemplo 8, ¿cuántos órdenes de magnitud\(C\) mayor es que\(B\)?
Solución
El valor\(B\) corresponde a\(10^2 = 100\)
El valor\(C\) corresponde a\(10^5 = 100,000\)
El cambio relativo es\(\dfrac{100,000}{100} = 1000 = \dfrac{10^5}{10^2} = 10^3\). El log de este valor es 3.
\(C\)es tres órdenes de magnitud mayor que\(B\), que se puede ver en la escala logarítmica por la diferencia visual entre los puntos de la escala.
Ejercicio\(\PageIndex{6}\)
Usando la mesa de Pruébalo Ahora #5, ¿cuál es la diferencia de orden de magnitud entre el sonido más suave que un humano puede escuchar y el lanzamiento del transbordador espacial?
- Contestar
-
\(\dfrac{2 \times 10^9}{2 \times 10^1} = 10^8\). La presión sonora en\(\mu\) Pa creada al lanzar el transbordador espacial es 8 órdenes de magnitud mayor que la presión sonora en\(\mu\) Pa creada por el sonido más suave que un oído humano puede escuchar.
Terremotos
Un ejemplo de una escala logarítmica es la Escala de Magnitud Momental (MMS) utilizada para sismos. Esta escala es comúnmente y erróneamente llamada Escala Richter, que fue una escala muy similar sucedida por el MMS.
Escala de magnitud de momento
Para un sismo con momento sísmico\(S\), una medición del movimiento de la tierra, el valor MMS, o la magnitud del sismo, es
\[M = \dfrac{2}{3} log(\dfrac{S}{S_0})\]
Dónde\(S_0 = 10^{16}\) se encuentra una medida de referencia para el momento sísmico.
Ejemplo\(\PageIndex{11}\)
Si un sismo tiene una magnitud MMS de 6.0, y otro tiene una magnitud de 8.0, ¿cuánto más poderoso (en términos de movimiento de la tierra) es el segundo terremoto?
Solución
Dado que el primer sismo tiene magnitud 6.0, podemos encontrar la cantidad de movimiento de la tierra para ese sismo, que vamos a denotar\(S_1\). El valor de no\(S_0\) es particularidad relevante, por lo que no vamos a reemplazarlo por su valor.
\[6.0 = \dfrac{2}{3} log (\dfrac{S_1}{S_0})\nonumber\]
\[6.0 (\dfrac{3}{2} = log (\dfrac{S_1}{S_0})\nonumber\]
\[9 = log(\dfrac{S_1}{S_0})\nonumber\]
\[\dfrac{S_1}{S_0} = 10^9\nonumber\]
\[S_1 = 10^9 S_0\nonumber\]
Esto nos dice que el primer sismo tiene aproximadamente\(10^9\) veces más movimiento de la tierra que la medida de referencia.
Haciendo lo mismo con el segundo sismo,\(S_2\), con una magnitud de 8.0,
\[8.0 = \dfrac{2}{3} log (\dfrac{S_2}{S_0})\nonumber\]
\[S_2 = 10^{12} S_0\nonumber\]
Comparando el movimiento terrestre del segundo terremoto con el primero,
\[\dfrac{S_2}{S_1} = \dfrac{10^{12} S_0} {10^9 S_0} = 10^3 = 1000\nonumber\]
El movimiento de la tierra del segundo valor es 1000 veces más grande que el primer terremoto.
Ejemplo\(\PageIndex{12}\)
Un sismo tiene una magnitud de 3.0. Si un segundo sismo tiene el doble de movimiento de la tierra que el primer terremoto, encuentre la magnitud del segundo sismo.
Solución
Desde que el primer sismo tiene magnitud 3.0,
\[3.0 = \dfrac{2}{3} log (\dfrac{S}{S_0})\nonumber\]
Resolviendo para\(S\),
\[3.0 \dfrac{3}{2} = log (\dfrac{S}{S_0})\nonumber\]
\[4.5 = log (\dfrac{S}{S_0})\nonumber\]
\[10^{4.5} = \dfrac{S}{S_0}\nonumber\]
\[S = 10^{4.5} S_0\nonumber\]
Dado que el segundo sismo tiene el doble de movimiento de la tierra, para el segundo sismo,
\[S = 2 \cdot 10^{4.5} S_0\nonumber\]
Encontrar la magnitud,
\[M = \dfrac{2}{3} log (\dfrac{2 \cdot 10^{4.5} S_0}{S_0})\nonumber\]
\[M = \dfrac{2}{3} log (2 \cdot 10^{4.5}) \approx 3.201\nonumber\]
El segundo sismo con el doble de movimiento de la tierra tendrá una magnitud de aproximadamente 3.2.
De hecho, usando propiedades logarítmicas, podríamos mostrar que siempre que el movimiento de la tierra se duplique, la magnitud aumentará en aproximadamente 0.201:
\[M = \dfrac{2}{3} log (\dfrac{2S}{S_0}) = \dfrac{2}{3} log (2 \cdot \dfrac{S}{S_0})\nonumber\]
\[M = \dfrac{2}{3} (log(2) + log(\dfrac{S}{S_0}))\nonumber\]
\[M = \dfrac{2}{3} log (2) + \dfrac{2}{3} log (\dfrac{S}{S_0})\nonumber\]
\[M = 0.201 + \dfrac{2}{3} log (\dfrac{S}{S_0})\nonumber\]
Esto ilustra la característica más importante de una escala logarítmica: que\(multiplying\) la cantidad que se está considerando se\(add\) ajustará al valor de la escala, y viceversa.
Temas Importantes de esta Sección
- Desintegración radiactiva
- Vida media
- Tiempo de duplicación
- La ley del enfriamiento de Newton
- Escalas logarítmicas
- Órdenes de Magnitud
- Escala Momento Magnitud


