4.6.6E: Modelos Exponenciales y Logarítmicos (Ejercicios)
- Page ID
- 116903
Sección 4.6 Ejercicio
1. Acudes al médico y él te inyecta 13 miligramos de tinte radiactivo. Después de 12 minutos, quedan 4.75 miligramos de tinte en su sistema. Para salir del consultorio del médico, debes pasar por un detector de radiación sin hacer sonar la alarma. Si el detector hace sonar la alarma cada vez que hay más de 2 miligramos del tinte en su sistema, ¿cuánto tiempo tomará su visita al médico, asumiendo que le dieron el tinte en cuanto llegó y la cantidad de tinte se descompone exponencialmente?
2. Toma 200 miligramos de un medicamento para el dolor de cabeza, y después de 4 horas, quedan 120 miligramos en tu sistema. Si los efectos del medicamento desaparecen cuando quedan menos de 80 miligramos, ¿cuándo necesitará tomar una segunda dosis, asumiendo que la cantidad de medicamento en su sistema decae exponencialmente?
3. La vida media de Radium-226 es de 1590 años. Si una muestra contiene inicialmente 200 mg, ¿cuántos miligramos quedarán después de 1000 años?
4. La vida media de Fermio-253 es de 3 días. Si una muestra contiene inicialmente 100 mg, ¿cuántos miligramos quedarán después de 1 semana?
5. La vida media del Erbio-165 es de 10.4 horas. Después de 24 horas una muestra aún contiene 2 mg. ¿Cuál fue la masa inicial de la muestra y cuánto quedará después de otros 3 días?
6. La vida media del Nobelio-259 es de 58 minutos. Después de 3 horas una muestra aún contiene 10 mg. ¿Cuál fue la masa inicial de la muestra, y cuánto quedará después de otras 8 horas?
7. Un científico comienza con 250 gramos de una sustancia radiactiva. Después de 225 minutos, la muestra ha decaído a 32 gramos. Encuentra la vida media de esta sustancia.
8. Un científico comienza con 20 gramos de una sustancia radiactiva. Después de 7 días, la muestra ha decaído a 17 gramos. Encuentra la vida media de esta sustancia.
9. Un artefacto de madera de una excavación arqueológica contiene el 60 por ciento del carbono-14 que está presente en los árboles vivos. ¿Hace cuánto tiempo se hizo el artefacto? (La vida media del carbono-14 es de 5730 años.)
10. Un artefacto de madera de una excavación arqueológica contiene 15 por ciento del carbono-14 que está presente en los árboles vivos. ¿Hace cuánto tiempo se hizo el artefacto? (La vida media del carbono-14 es de 5730 años.)
11. Un cultivo de bacterias inicialmente contiene 1500 bacterias y se duplica en tamaño cada media hora. Encontrar el tamaño de la población después de: a) 2 horas b) 100 minutos
12. Un cultivo de bacterias inicialmente contiene 2000 bacterias y se duplica en tamaño cada media hora. Encontrar el tamaño de la población después de: a) 3 horas b) 80 minutos
13. El recuento de bacterias en un cultivo fue de 800 después de 10 minutos y 1800 después de 40 minutos.
a. ¿Cuál fue el tamaño inicial de la cultura?
b. Encuentra el tiempo de duplicación.
c. Encontrar la población después de 105 minutos.
d. ¿Cuándo llegará la población a 11000?
14. El recuento de bacterias en un cultivo fue de 600 después de 20 minutos y 2000 después de 35 minutos.
a. ¿Cuál fue el tamaño inicial de la cultura?
b. Encuentra el tiempo de duplicación.
c. Encontrar la población después de 170 minutos.
d. ¿Cuándo llegará la población a 12000?
15. Encuentra el tiempo requerido para que una inversión duplique su valor si se invierte en una cuenta pagando 3% compuesto trimestralmente.
16. Encontrar el tiempo requerido para que una inversión duplique su valor si se invierte en una cuenta pagando 4% compuesto mensualmente
17. El número de cristales que se han formado después de t horas viene dado por\(n\left(t\right)=20e^{0.013t}\). ¿Cuánto tiempo tarda el número de cristales en duplicarse?
18. El número de permisos de construcción en Pasco t años después de 1992 siguió aproximadamente la ecuación\(n\left(t\right)=400e^{0.143t}\). ¿Cuál es el tiempo de duplicación?
19. Se saca un pavo del horno cuando la temperatura interna es\(165^{\circ}\) Fahrenheit, y se deja enfriar en una\(75^{\circ}\) habitación. Si la temperatura del pavo es\(145^{\circ}\) después de media hora,
a. ¿Cuál será la temperatura después de 50 minutos?
b. ¿Cuánto tiempo tardará el pavo en enfriarse al 110\(\mathrm{{}^\circ}\)?
20. Se vierte una taza de café a\(190^{\circ}\) Fahrenheit, y se deja enfriar en una\(70^{\circ}\) habitación. Si la temperatura del café es\(170^{\circ}\) después de media hora,
a. ¿Cuál será la temperatura después de 70 minutos?
b. ¿Cuánto tiempo tardará el café en enfriarse a\(120^{\circ}\)\)?
21. La población de peces en un lago abastecido en una granja después de t años podría modelarse por la ecuación\(P\left(t\right)=\dfrac{1000}{1+9e^{-0.6t} }\).
a. Esbozar una gráfica de esta ecuación.
b. ¿Cuál es la población inicial de peces?
c. ¿Cuál será la población después de 2 años?
d. ¿Cuánto tiempo tardará la población en llegar a 900?
22. El número de personas en un pueblo que han escuchado un rumor después de t días puede ser modelado por la ecuación\(N\left(t\right)=\dfrac{500}{1+49e^{-0.7t} }\).
a. Esbozar una gráfica de esta ecuación.
b. ¿Cuánta gente empezó el rumor?
c. ¿Cuántas personas han escuchado el rumor después de 3 días?
d. ¿Cuánto tiempo pasará hasta que 300 personas hayan escuchado el rumor?
Encuentra el valor del número mostrado en cada escala logarítmica
23.  24.
24. 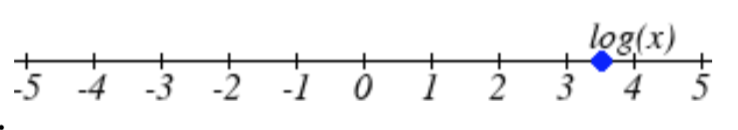
25. 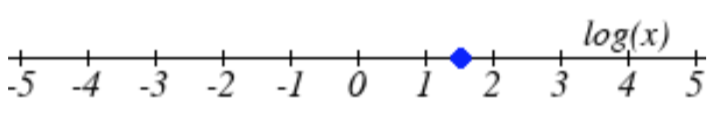 26.
26. 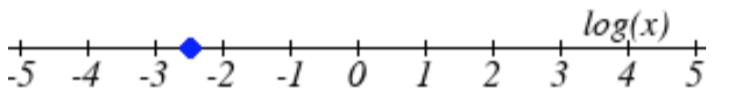
Trazar cada conjunto de valores aproximados en una escala logarítmica.
27. Intensidad de los sonidos: Susurro:\(10^{-10} W/m^{2}\), Vacío:\(10^{-4} W/m^{2}\), Chorro:\(10^{2} W/m^{2}\)
28. Misa: Amoeba:\(10^{-5} g\), Humano:\(10^{5} g\), Estatua de la Libertad:\(10^{8} g\)
29. El terremoto de San Francisco de 1906 tuvo una magnitud de 7.9 en la escala MMS. Posteriormente se produjo un sismo de magnitud 4.7 que causó sólo daños menores. ¿Cuántas veces más intenso fue el sismo de San Francisco que el segundo?
30. El terremoto de San Francisco de 1906 tuvo una magnitud de 7.9 en la escala MMS. Posteriormente se produjo un sismo con magnitud 6.5 que causó menos daños. ¿Cuántas veces más intenso fue el sismo de San Francisco que el segundo?
31. Un sismo tiene magnitud 3.9 en la escala MMS. Si un segundo sismo tiene 750 veces más energía que el primero, encuentra la magnitud del segundo sismo.
32. Un sismo tiene una magnitud 4.8 en la escala MMS. Si un segundo sismo tiene 1200 veces más energía que el primero, encuentra la magnitud del segundo sismo.
33. Se estima que una colonia de células de levadura contiene 10\({}^{6}\) células a la vez\(t = 0\). Después de recolectar datos experimentales en el laboratorio, usted decide que la población total de células en\(t\) horas de tiempo viene dada por la función\(f\left(t\right)=10^{6} e^{0.495105t}\). [UW]
a. ¿Cuántas células hay presentes después de una hora?
b. ¿Cuánto tiempo tarda de la población en duplicarse?.
c. Cherie, otro miembro de tu laboratorio, mira tu cuaderno y dice: “Esa fórmula es incorrecta, mis cálculos predicen que la fórmula para el número de células de levadura viene dada por la función. \(f\left(t\right)=10^{6} \left(2.042727\right)^{0.693147t}\).” ¿Deberías estar preocupado por el comentario de Cherie?
d. Anja, un tercer miembro de su laboratorio que trabaja con las mismas células de levadura, tomó estas dos medidas:\(7.246\times 10^{6}\) células después de 4 horas;\(16.504\times 10^{6}\) células después de 6 horas. ¿Deberías estar preocupado por los resultados de Anja? Si las mediciones de Anja son correctas, ¿su modelo sobreestima o subestima el número de células de levadura a la vez\(t\)?
34. A medida que la luz de la superficie penetra en el agua, su intensidad disminuye. En las aguas cristalinas del Caribe, la intensidad disminuye un 15 por ciento por cada 3 metros de profundidad. Así, la intensidad tendrá la forma de una función exponencial general. [UW]
a. si la intensidad de la luz en la superficie del agua es\(I_{0}\), encontrar una fórmula para\(I(d)\), la intensidad de la luz a una profundidad de\(d\) metros. Tu fórmula debe depender de\(I_{0}\) y\(d\).
b. ¿A qué profundidad disminuirá la intensidad lumínica al 1% de su intensidad superficial?
35. La mioglobina y la hemoglobina son moléculas transportadoras de oxígeno en el cuerpo humano. La hemoglobina se encuentra dentro de los glóbulos rojos, que fluyen de los pulmones a los músculos a través del torrente sanguíneo. La mioglobina se encuentra en las células musculares. La función\(Y=M\left(p\right)=\dfrac{p}{1+p}\) calcula la fracción de mioglobina saturada de oxígeno a una presión determinada\(p\) Torrs. Por ejemplo, a una presión de 1 Torr\(M(1) = 0.5\), lo que significa que la mitad de la mioglobina (es decir, 50%) está saturada de oxígeno. (Nota: Más precisamente, es necesario usar algo llamado la “presión parcial”, pero la distinción no es importante para este problema.) Asimismo, la función\(Y=H\left(p\right)=\dfrac{p^{2.8} }{26^{2.8} +p^{2.8} }\) calcula la fracción de hemoglobina saturada de oxígeno a una presión dada\(p\). [UW]
a. Las gráficas de\(M(p)\) y\(H(p)\) se dan aquí sobre el dominio\(0 \le p \le 100\); ¿cuál es cuál?
b. Si la presión en los pulmones es de 100 Torrs, ¿cuál es el nivel de saturación de oxígeno de la hemoglobina en los pulmones?
c. La presión en un músculo activo es de 20 Torrs. ¿Cuál es el nivel de saturación de oxígeno de la mioglobina en un músculo activo? ¿Cuál es el nivel de hemoglobina en un músculo activo?
d. Definir la eficiencia del transporte de oxígeno a una presión dada\(p\) a ser\(M(p) - H(p)\). ¿Cuál es la eficiencia del transporte de oxígeno a 20 Torrs? ¿A 40 Torrs? ¿A 60 Torrs? Esbozar la gráfica de\(M(p) - H(p)\); ¿existen condiciones bajo las cuales se maximiza la eficiencia del transporte (explique)?
36. La longitud de algunos peces está modelada por una función de crecimiento de von Bertalanffy. Para el fletán del Pacífico, esta función tiene la forma\(L\left(t\right)=200\left(1-0.957e^{-0.18t} \right)\) donde\(L(t)\) está la longitud (en centímetros) de un pez de t años. [UW]
a. ¿Cuál es la longitud de un fletán recién nacido al nacer?
b. Utilice la fórmula para estimar la longitud de un fletán de 6 años de edad.
c. ¿A qué edad esperarías que el halibut tuviera 120 cm de largo?
d. ¿Cuál es la significación práctica (física) del número 200 en la fórmula para\(L(t)\)?
37. Una célula cancerosa carece de regulación normal del crecimiento biológico y puede dividirse continuamente. Supongamos que una sola célula cutánea de ratón es cancerosa y su ciclo celular mitótico (el tiempo para que la célula se divida una vez) es de 20 horas. El número de celdas a la vez\(t\) crece de acuerdo con un modelo exponencial. [UW]
a. Encontrar una fórmula\(C(t)\) para el número de células cancerosas de la piel después de\(t\) horas.
b. Supongamos que una célula típica de piel de ratón es esférica de radio\(50 \times 10^{-4}\) cm. Encuentra el volumen combinado de todas las células cancerosas de la piel después de\(t\) horas. ¿Cuándo será el volumen de células cancerosas de 1 cm\({}^{3}\)?
38. Un barco se embarcó en un largo viaje. Al inicio del viaje, había 500 hormigas en la bodega de carga del buque. A una semana del viaje, había 800 hormigas. Supongamos que la población de hormigas es una función exponencial del tiempo. [UW]
a. ¿Cuánto tiempo tardó en duplicarse la población?
b. ¿Cuánto tiempo tardó la población en triplicarse?
c. ¿Cuándo había 10,000 hormigas a bordo?
d. También hubo una población exponencialmente creciente de osos hormigueros a bordo. Al inicio del viaje había 17 osos hormigueros, y la población de osos hormigueros se duplicó cada 2.8 semanas. ¿Cuánto tiempo en el viaje hubo 200 hormigas por oso hormiguero?
39. Las poblaciones de termitas y arañas en una determinada casa están creciendo exponencialmente. La casa contiene 100 termitas el día que te mudas. Después de 4 días, la casa contiene 200 termitas. Tres días después de mudarse, hay dos veces más termitas que arañas. Ocho días después de mudarse, había cuatro veces más termitas que arañas. ¿Cuánto tiempo (en días) tarda la población de arañas en triplicarse? [UW]
- Contestar
-
1. \(f(t) = 13(0.9195)^t\). Quedarán 2 mg después de 22.3098 minutos
3. \(f(t) = 200 (0.999564)^t\). \(f(1000) = 129.3311\)mg
5. \(r = -0.06448\). Masa inicial: 9.9018 mg. Después de 3 días: 0.01648 mg
7. \(f(t) = 250 (0.9909)^t\). Vida media = 75.8653 minutos
9. \(f(t) = a(0.999879)^t\). 60% (0.60\(a\)) permanecería después de 4222.813 años
11. \(P(t) = 1500(1.02337)^t\)(\(t\)en minutos).
Después de 2 horas = 24000.
Después de 100 minutos = 1511913. a) 610.5143 (aproximadamente 611)
b) 25. 6427 minutos
c) 10431.21
d). 106.9642 minutos15. 23.1914 años
17. 53.319 horas
19. \(T(t) =. 90(0.99166)^t + 75\).
a). 134.212 grados
b). 112.743 minutos21. a).
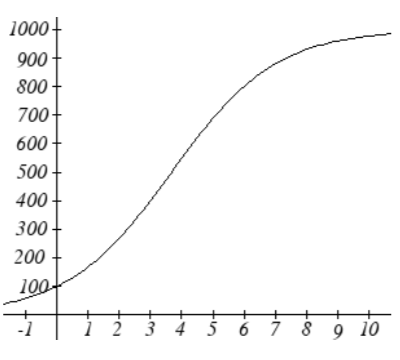
b). 100
c). 269.487
d). 7.324 años23. \(\text{log}(x) = -0.5. x = 0.3162\)
25. \(\text{log}(x). = 1.5. x = 31.623\)
27.

29. 63095.7 veces más intenso
31. Magnitud MMS 5.817
33. a). alrededor de 1640671
b). 1.4 horas
c). No, porque\((2.042727)^{0.693147} \approx e^{0.495104}\)
d). Los datos de Anja predicen una tasa de crecimiento continuo de 0.4116, que es mucho menor que la tasa 0.495105 que calculaste. Nuestro modelo sobreestimaría el número de células.35. a) La curva que aumenta rápidamente al principio es\(M(p)\)
b)\(H(100) = 0.9775\)
c) Mioglobina:\(M(20) = 0.9524\). Hemoglobina:\(H(20) = 0.3242\)
d) A 20 torrs: 0.6282. A 40 torrs: 0.2060. A 60 torrs: 0.0714
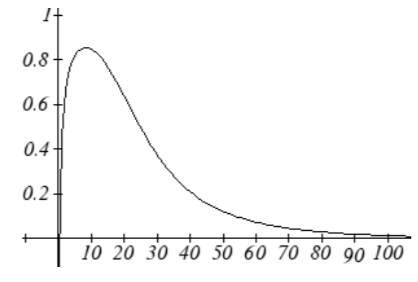 La eficiencia parece estar maximizada a aproximadamente 8 torr
La eficiencia parece estar maximizada a aproximadamente 8 torr37. a)\(C(t) = 1.03526^t\), o\(C(t) = e^{0.03466t}\)
b) Volumen de una celda:\(\dfrac{4}{3} \pi (50 \times 10^{-4})^3 \approx 5.236 \times 10^{-7} \text{cm}^3\), así necesitará alrededor de\(1.9099 \times 10^{6}\) celdas para un volumen de 1\(\text{cm}^3\). \(C(t) = 1.9099 \times 10^6\)después de 417.3 horas39. 31.699 días


