4.7: Ajuste de modelos exponenciales a los datos
- Page ID
- 116807
En la sección anterior, vimos líneas numéricas usando escalas logarítmicas. También es común ver gráficas bidimensionales con uno o ambos ejes usando una escala logarítmica.
Un uso común de una escala logarítmica en el eje vertical es graficar cantidades que están cambiando exponencialmente, ya que ayuda a revelar diferencias relativas. Esto se usa comúnmente en los gráficos bursátiles, ya que los valores históricamente han crecido exponencialmente con el tiempo. Ambos gráficos bursátiles a continuación muestran el Promedio Industrial Dow Jones, de 1928 a 2010.
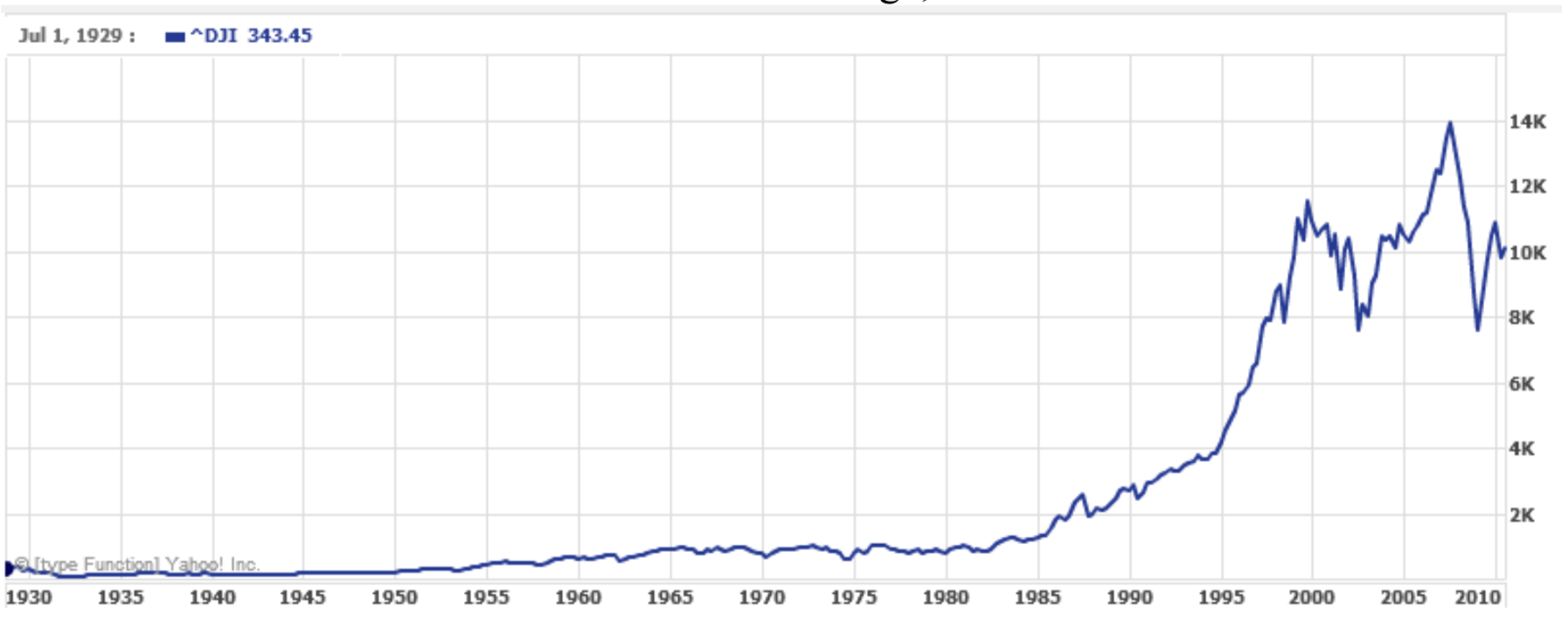
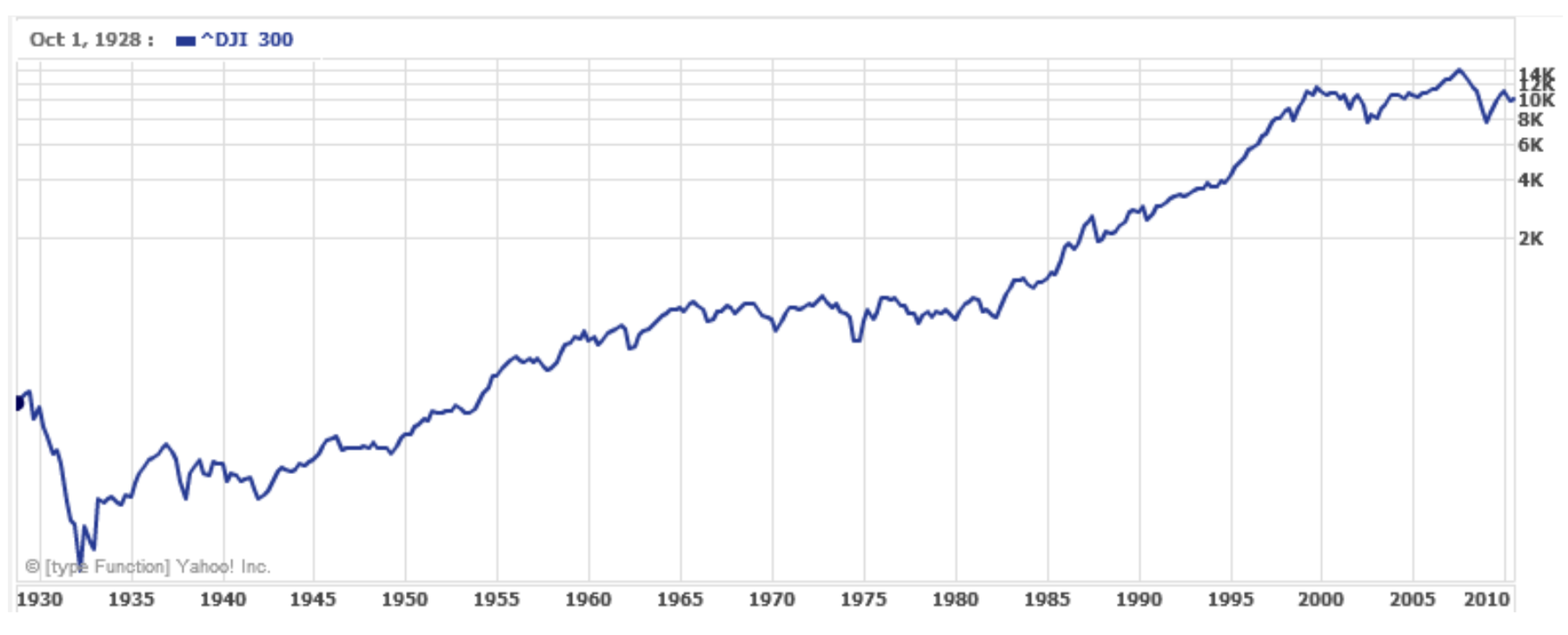
Ambas gráficas tienen una escala horizontal lineal, pero la primera gráfica tiene una escala vertical lineal, mientras que la segunda tiene una escala vertical logarítmica. La primera escala es la que más conocemos, y muestra lo que parece ser una fuerte tendencia exponencial, al menos hasta el año 2000.
Ejemplo\(\PageIndex{1}\)
Hubo caídas bursátiles en 1929 y 2008. ¿Cuál era más grande?
Solución
En la primera gráfica, la caída del mercado de valores alrededor de 2008 parece muy grande, y en términos de valores en dólares, de hecho fue una gran caída. Sin embargo, la segunda gráfica muestra cambios relativos, y la caída en 2009 parece menos importante en esta gráfica, y de hecho la caída a partir de 1929 fue, en términos porcentuales, mucho más significativa.
Específicamente, en 2008, el valor del Dow bajó de alrededor de 14,000 a 8,000, una caída de 6,000. Esto es obviamente una gran caída de valor, y equivale a una caída de alrededor del 43%. En 1929, el valor del Dow bajó de un máximo de alrededor de 380 a un mínimo de 42 en julio de 1932. Si bien en términos de valor esta caída de 338 es mucho menor que la caída de 2008, corresponde a una caída de 89%, una caída relativa mucho mayor que en 2008. La escala logarítmica muestra estos cambios relativos.
La segunda gráfica anterior, en la que un eje utiliza una escala lineal y el otro eje usa una escala logarítmica, es un ejemplo de una gráfica semilogarítmica.
Definición: GRÁFICOS semi-log y log-log
Una gráfica semilogarítmica es una gráfica con un eje usando una escala lineal y un eje usando una escala logarítmica.
Un gráfico logarítmico es un gráfico con ambos ejes usando escalas logarítmicas.
Ejemplo\(\PageIndex{2}\)
Trazar 5 puntos en la gráfica de\(f(x)=3(2)^{x}\) en una gráfica semilogarítmica con una escala logarítmica en el eje vertical.
Solución
Para ello, necesitamos encontrar 5 puntos en la gráfica, luego calcular el logaritmo del valor de salida. Elegir arbitrariamente 5 valores de entrada,
| \(x\) | \(f(x)\) | registro (\(f(x)\)) |
| -3 | \(3(2)^{-1} = \dfrac{3}{8}\) | -0.426 |
| -1 | \(3(2)^{-1} = \dfrac{3}{2}\) | 0.176 |
| 0 | \(3(2)^{0} = 3\) | 0.477 |
| 2 | \(3(2)^{2} = 12\) | 1.079 |
| 5 | \(3(2)^{5} = 96\) | 1.982 |
Trazar estos valores en una gráfica semilogarítmica,
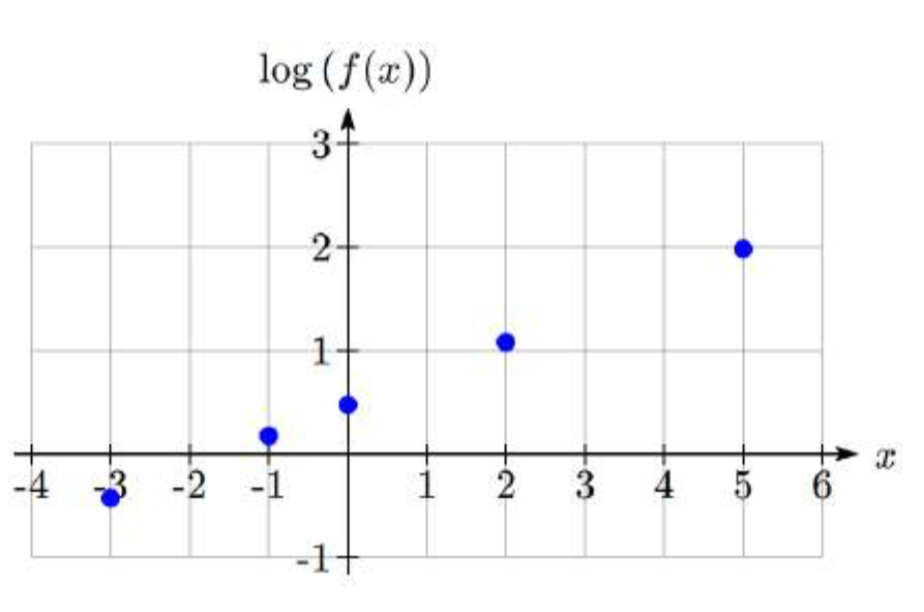
Observe que en esta escala semilogarítmica, los valores de la función exponencial aparecen lineales. Podemos mostrar que este comportamiento se espera mediante la utilización de propiedades logarítmicas. Para la función\(f(x)=ab^{x}\), encontrar log (\(f(x)\)) da
\[\log \left(f(x)\right)=\log \left(ab^{x} \right)\nonumber\]Utilizando la propiedad sum de logs,
\[\log \left(f(x)\right)=\log \left(a\right)+\log \left(b^{x} \right)\nonumber\] ahora utilizando la propiedad exponente,
\[\log \left(f(x)\right)=\log \left(a\right)+x\log \left(b\right)\nonumber\]
Esta relación es lineal, con log (a) como intercepción vertical, y log (b) como pendiente. Esta relación también se puede utilizar a la inversa.
Ejemplo\(\PageIndex{3}\)
Se traza una gráfica exponencial en ejes semilogarítmicos. Encuentra una fórmula para la función exponencial\(g(x)\) que generó esta gráfica.
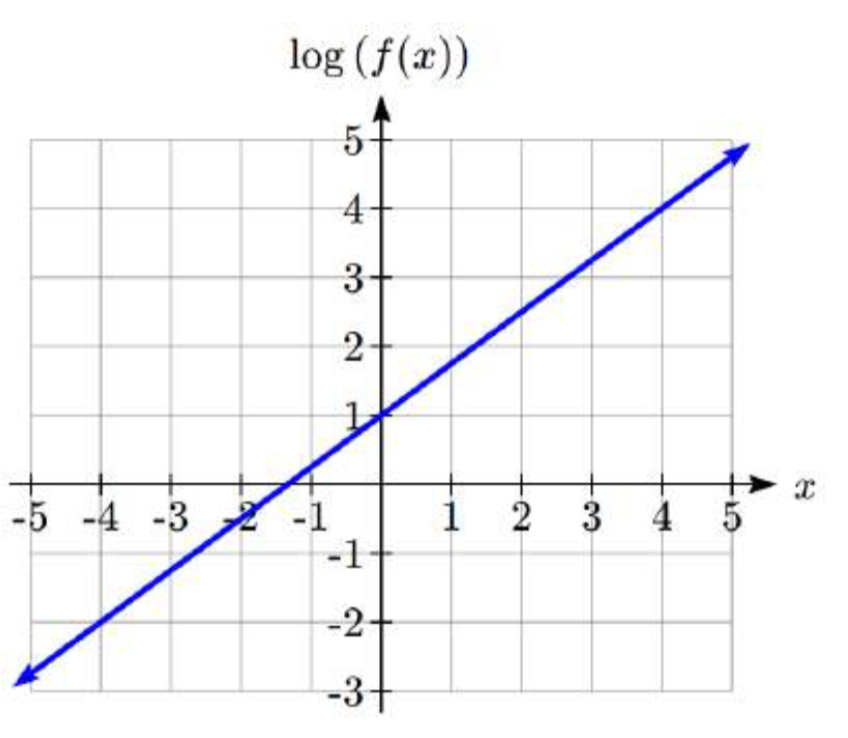
Solución
La gráfica es lineal, con intercepción vertical en (0, 1). Al observar el cambio entre los puntos (0, 1) y (4, 4), podemos determinar la pendiente de la línea es\(\dfrac{3}{4}\). Dado que la salida es log (\(g(x)\)), esto lleva a la ecuación\(\log \left(g(x)\right)=1+\dfrac{3}{4} x\).
Podemos resolver esta fórmula\(g(x)\) reescribiendo en forma exponencial y simplificando:
\[\log \left(g(x)\right)=1+\dfrac{3}{4} x\nonumber\]Reescribir como exponencial,
\[g(x)=10^{1+\dfrac{3}{4} x}\nonumber\] Romper esto usando reglas de exponente,
\[g(x)=10^{1} \cdot 10^{\dfrac{3}{4} x}\nonumber\] Usar reglas de exponente para agrupar el segundo factor,
\[g(x)=10^{1} \cdot \left(10^{\dfrac{3}{4} } \right)^{x}\nonumber\] Evaluar los poderes de 10,
\[g(x)=10\left(5.623\right)^{x}\nonumber\]
Ejercicio\(\PageIndex{1}\)
Una gráfica exponencial se traza en una gráfica semilogarítmica a continuación. Encuentra una fórmula para la función exponencial\(g(x)\) que generó esta gráfica.
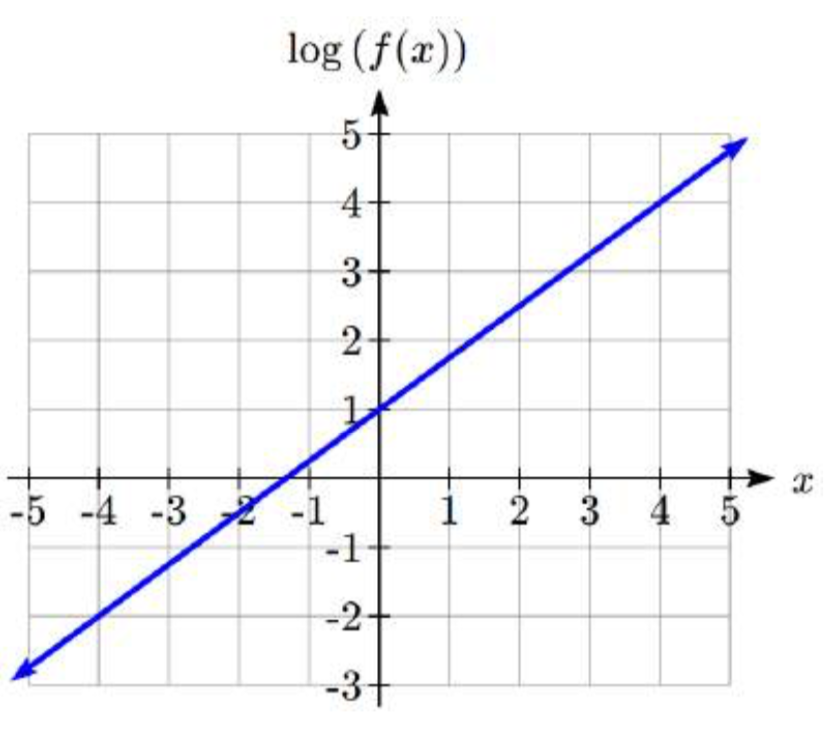
- Contestar
-
\[g(x) = 10^{2 - 0.5x} = 10^2 (10^{-0.5})^{x},\quad f(x) = 100 (0.3162)^x\nonumber\]
Ajuste de funciones exponenciales a los datos
Algunas opciones de tecnología proporcionan funciones dedicadas para encontrar funciones exponenciales que se ajusten a los datos, pero muchas solo proporcionan funciones para ajustar funciones lineales a los datos. La escala semi-logarítmica nos proporciona un método para ajustar una función exponencial a los datos construyendo sobre las técnicas que tenemos para ajustar funciones lineales a los datos.
para ajustar una función exponencial a un conjunto de datos mediante linealización
- Buscar el registro de los valores de salida de datos
- Encuentre la ecuación lineal que se ajuste a los pares (entrada, log (salida)). Esta ecuación será del formulario log (\(f(x)\)) =\(b + mx\).
- Resolver esta ecuación para la función exponencial\(f(x)\)
Ejemplo\(\PageIndex{4}\)
En la siguiente tabla se muestra el costo en dólares por megabyte de espacio de almacenamiento en discos duros de computadora de 1980 a 2004, y los datos se muestran en una gráfica estándar a la derecha, con la entrada cambiada a años después de 1980.
\ (\ begin {array} {|l|l|}
\ hline\ text {Año} &\ texto {Costo por MB}\\
\ hline 1980 & 192.31\
\ hline 1984 & 87.86\\
\ hline 1988 & 15.98\
\ hline 1992 & 4\\
\ hline 1996 & 0.173\\
\ hline hline 2000 & 0.006849\\
\ hline 2004 & 0.001149\\
\ hline
\ end {array}\)
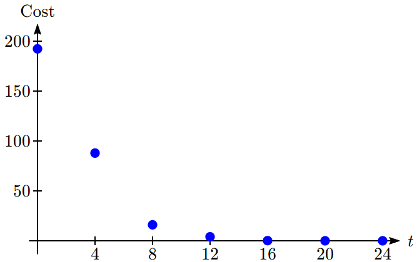
Estos datos parecen estar disminuyendo exponencialmente. Para encontrar una función que modele esta decadencia, comenzaríamos por encontrar el registro de los costos.
\ (\ begin {array} {|l|l|l|l|}
\ hline\ text {Año} & t &\ text {Costo por MB} &\ log (\ text {Costo})\
\\ hline 1980 & 0 & 192.31 & 2.284002\
\ hline 1984 & 4 & 87.86 & 1.943791\
\ hline 1988 & 8 & 15.98 & 1.203577\
\ hline 1992 & 12 & 4 & 0.60206\
\ hline 1996 & 16 & 0.173 & -0.76195\
\ hline 2000 & 20 & 0.006849 & -2.16437\
\ hline 2004 & 24 & 0.001149 & -2.93952\
\ hline
\ end {array}\)
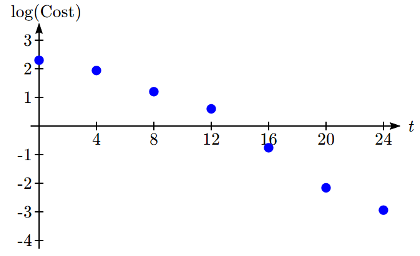
Solución
Como se esperaba, la gráfica del log de costos parece bastante lineal, sugiriendo que una función exponencial se ajustará a los datos originales encajará razonablemente bien. Usando la tecnología, podemos encontrar una ecuación lineal para ajustar los valores de log (Costo). Usando\(t\) como años después de 1980, la regresión lineal da la ecuación:
\[\log (C(t))=2.794-0.231t\nonumber\]
Resolviendo para\(C(t)\),
\[C(t)=10^{2.794-0.231t}\nonumber\]
\[C(t)=10^{2.794} \cdot 10^{-0.231t}\nonumber\]
\[C(t)=10^{2.794} \cdot \left(10^{-0.231} \right)^{t}\nonumber\]
\[C(t)=622\cdot \left(0.5877\right)^{t}\nonumber\]
Esta ecuación sugiere que el costo por megabyte para el almacenamiento en discos duros de computadora está disminuyendo alrededor de 41% cada año.
Usando esta función, podríamos predecir el costo de almacenamiento en el futuro. Predecir el costo en el año 2020 (\(t = 40\)):
\(C(40) =622\left(0.5877\right)^{40} \approx 0.000000364\)dólares por megabyte, un número muy pequeño. Eso equivale a $0.36 por terabyte de almacenamiento en disco duro.
Al comparar los valores predichos por este modelo con los datos reales, vemos que el modelo coincide con los datos originales en orden de magnitud, pero los valores específicos parecen bastante diferentes. Este es, desafortunadamente, el mejor modelo exponencial que puede ajustarse a los datos. Es posible que un modelo no exponencial se ajuste mejor a los datos, o simplemente podría haber una variabilidad lo suficientemente amplia en los datos como para que ningún modelo relativamente simple se ajustara mejor a los datos.
| Año | Costo real por MB | Costo previsto por modelo |
| 1980 | 192.31 | 622.3 |
| 1984 | 87.86 | 74.3 |
| 1988 | 15.98 | 8.9 |
| 1992 | 4 | 1.1 |
| 1996 | 0.173 | 0.13 |
| 2000 | 0.006849 | 0.015 |
| 2004 | 0.001149 | 0.0018 |
Ejercicio\(\PageIndex{2}\)
El siguiente cuadro muestra el valor\(V\), en miles de millones de dólares, de las importaciones estadounidenses procedentes de China\(t\) años después del 2000.
| año | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| \(t\) | 0 | 1 | 2 | 3 | 4 | 5 |
| \(V\) | 100 | 102.3 | 125.2 | 152.4 | 196 |
Estos datos parecen estar creciendo exponencialmente. Linealizar estos datos y construir un modelo para predecir cuántos miles de millones de dólares de importaciones se esperaban en 2011.
- Contestar
-
\(V(t) = 90.545 (1.2078)^t\). Prediciendo en 2011,\(V(11) = 722.45\) mil millones de dólares.
Temas Importantes de esta Sección
- Gráfico semilogargo
- Gráfica logarítmica
- Linealización de funciones exponenciales
- Ajuste de una ecuación exponencial a los datos


