6.1: Gráficas sinusoidales

Última actualización
Guardar como PDF

Page ID: 116671

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The London Eye (foto London Eye de autores, 2010, CC-BY) es una enorme noria de 135 metros (394 pies) de altura en $Foto de la noria London eye$ tierra de Londres, Eng, que completa una rotación cada 30 minutos. Cuando miramos el comportamiento de esta noria queda claro que completa 1 ciclo, o 1 revolución, y luego repite esta revolución una y otra vez.

Este es un ejemplo de una función periódica, porque la noria repite su revolución o un ciclo cada 30 minutos, y así decimos que tiene un periodo de 30 minutos.

En esta sección, trabajaremos para esbozar una gráfica de la altura de un ciclista sobre el suelo a lo largo del tiempo y expresar esta altura en función del tiempo.

Definición: Funciones periódicas

Una función periódica es una función para la cual un desplazamiento horizontal específico,$P$, da como resultado la función original:$f(x+P)=f(x)$ para todos los valores de$x$. Cuando esto ocurre llamamos al menor desplazamiento horizontal de este tipo con$P > 0$ el periodo de la función.

De inmediato podrías adivinar que aquí hay una conexión para encontrar puntos en un círculo, ya que la altura sobre el suelo correspondería al$y$ valor de un punto en el círculo. Podemos determinar el$y$ valor usando la función sinusoidal. Para tener una mejor idea del comportamiento de esta función, podemos crear una tabla de valores que conocemos, y utilizarlos para esbozar una gráfica de las funciones seno y coseno.

Listado de algunos de los valores de seno y coseno en un círculo unitario,

*$\theta$*	0	$\dfrac{\pi }{6}$	$\dfrac{\pi }{4}$	$\dfrac{\pi }{3}$	$\dfrac{\pi }{2}$	$\dfrac{2\pi }{3}$	$\dfrac{3\pi }{4}$	$\dfrac{5\pi }{6}$	$\pi$
cos	1	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{1}{2}$	0	$-\dfrac{1}{2}$	$-\dfrac{\sqrt{2} }{2}$	$-\dfrac{\sqrt{3} }{2}$	-1
pecado	0	$\dfrac{1}{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{\sqrt{3} }{2}$	1	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{1}{2}$	0

Aquí puedes ver cómo para cada ángulo, usamos el$y$ valor del punto en el círculo para determinar el valor de salida de la función sinusoidal.

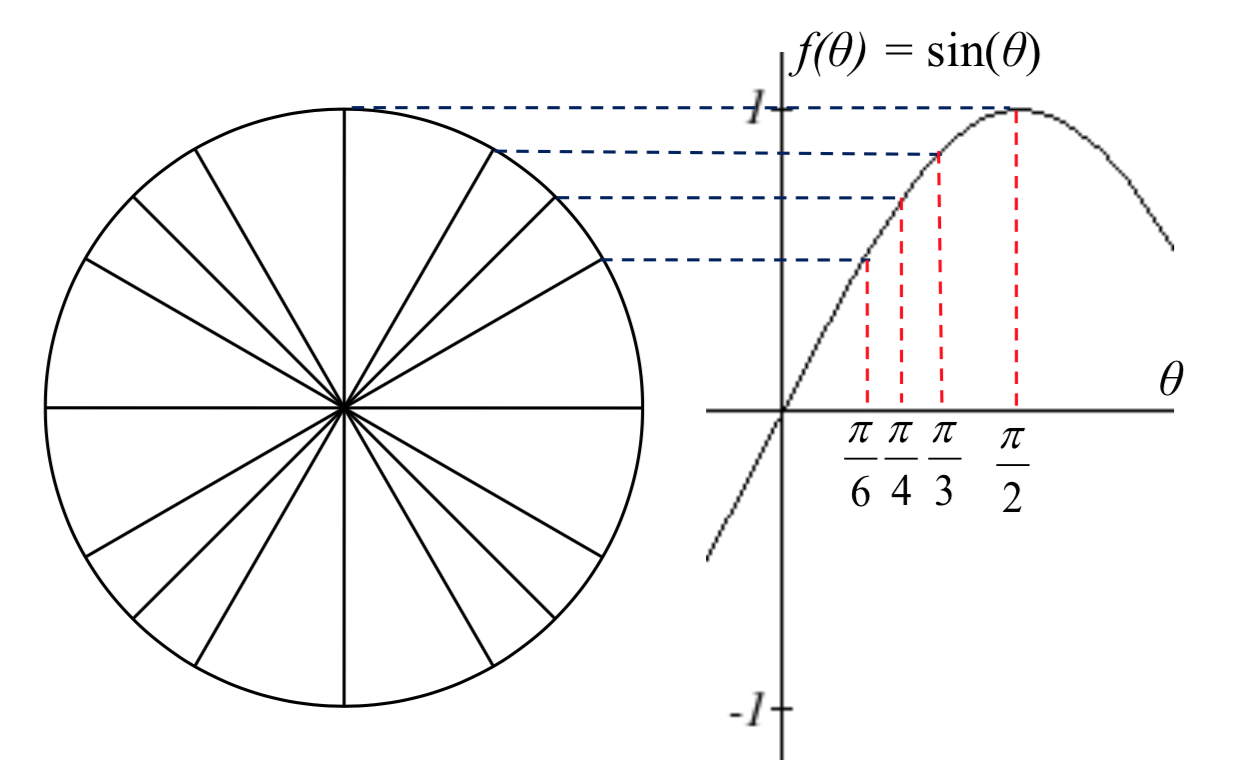
$A la izquierda hay un círculo, y a la derecha hay un conjunto de ejes, la horizontal etiquetada theta y la vertical etiquetada f de theta es igual a seno de theta, mostrando una gráfica que aumenta cóncava hacia abajo luego cambia a decaer cóncava hacia abajo. En el círculo hay líneas en ángulos pi sobre 6, pi sobre 4, pi sobre 3 y pi sobre 2. Donde esas líneas tocan el círculo, una línea discontinua horizontal conduce se conecta a puntos en la gráfica sinusoidal donde las coordenadas horizontales corresponden con el ángulo en el círculo.$

Trazar más puntos da la forma completa de las funciones seno y coseno.

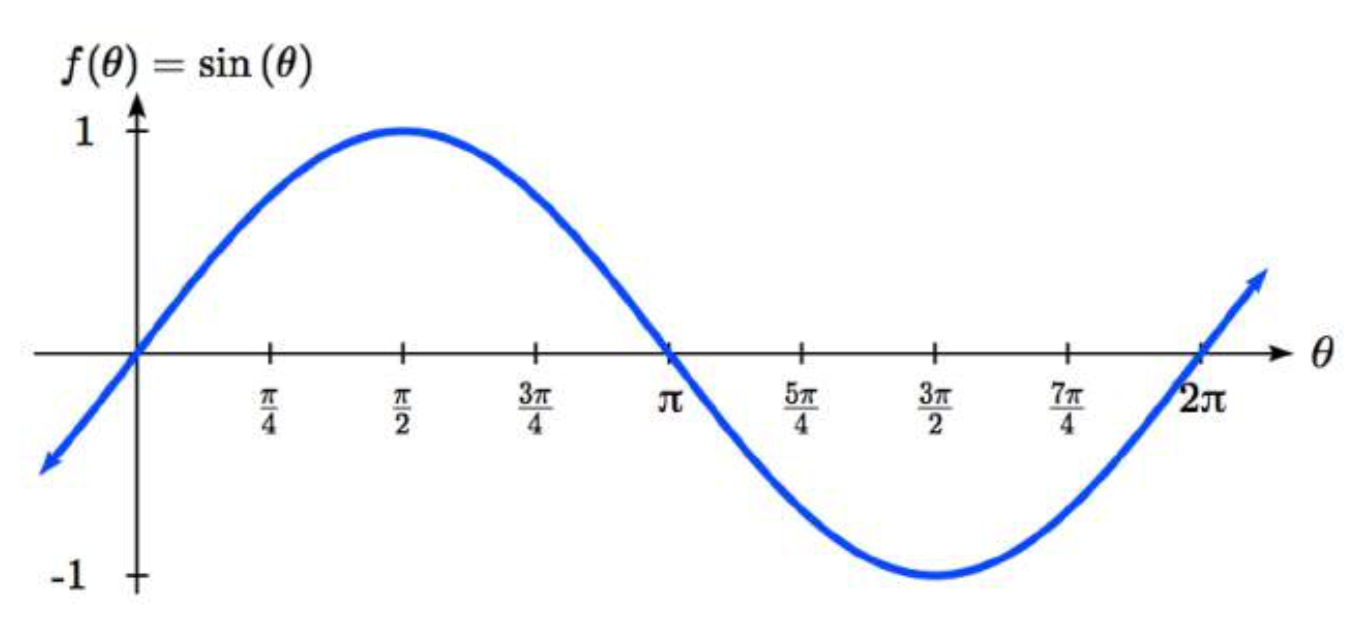
$Una gráfica sinusoidal, mostrada de theta es igual a 0 a 2 pi. El gráfico comienza aumentando en 0 coma 0. La gráfica es cóncava hacia abajo ya que alcanza el pico en pi sobre 2 coma 1. Disminuye cóncava hasta pi coma 0, luego disminuye cóncava hasta 3 pi sobre 2 comas negativas 1. Aumenta cóncava hasta 2 pi coma 0. La gráfica continúa más allá de esto, repitiendo la misma forma.$

Observe cómo los valores sinusoidales son positivos entre 0 y$\pi $, que corresponden a los valores de seno en los cuadrantes 1 y 2 en el círculo unitario, y los valores sinusoidales son negativos entre$\pi $ y 2$\pi $, correspondientes a los cuadrantes 3 y 4.

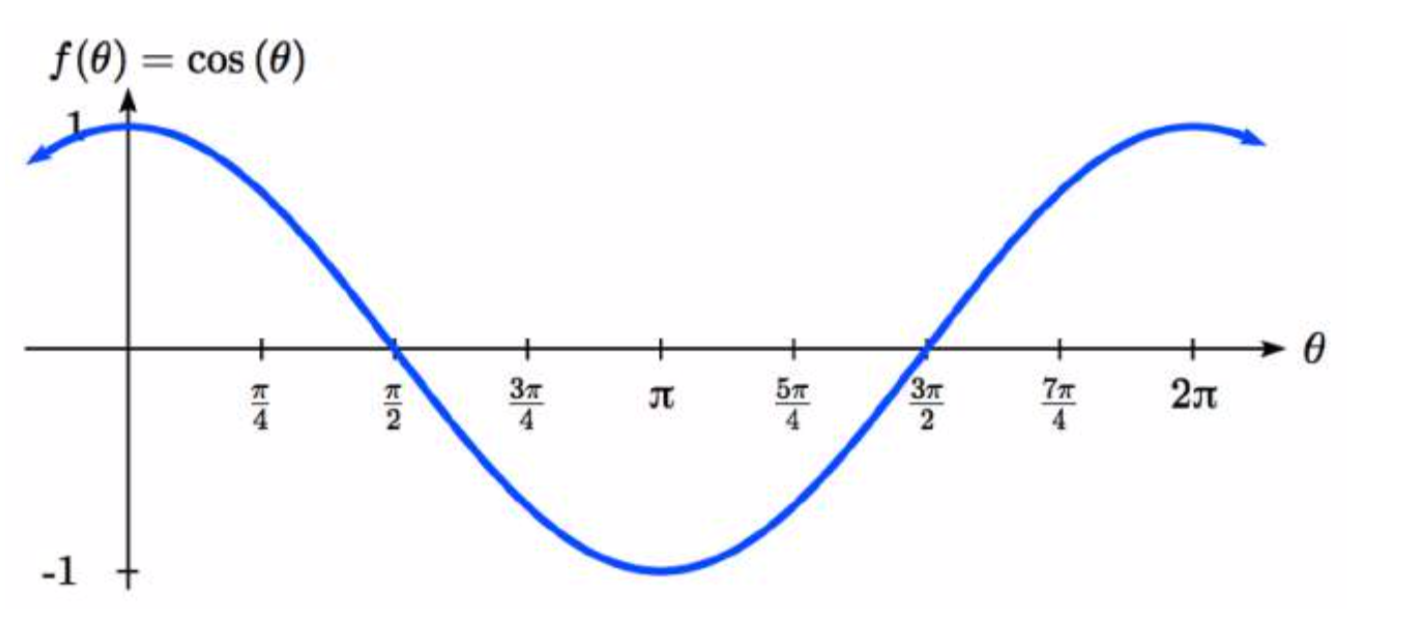
$Una gráfica coseno, mostrada de theta es igual a 0 a 2 pi. La gráfica comienza en 0 coma 1, y disminuye cóncava abajo a pi sobre 2 coma 0, luego disminuye cóncava hasta pi coma negativa 1. Luego aumenta cóncavo hasta 3 pi sobre 2 coma 0, y aumenta cóncavo hasta 2 pi coma 1. La gráfica continúa más allá de esto, repitiendo la misma forma.$

Al igual que la función seno podemos rastrear el valor de la función coseno a través de los 4 cuadrantes del círculo unitario a medida que lo colocamos en una gráfica.

Ambas funciones están definidas para todos los números reales, ya que podemos evaluar el seno y el coseno de cualquier ángulo. Al pensar en el seno y el coseno como coordenadas de puntos en un círculo unitario, queda claro que el rango de ambas funciones debe ser el intervalo [-1, 1].

Dominio y rango de seno y coseno

El dominio de seno y coseno es todo números reales,$(-\infty ,\infty )$.

El rango de seno y coseno es el intervalo [-1, 1].

Ambas gráficas se denominan gráficas sinusoidales.

En ambas gráficas, la forma de la gráfica comienza a repetirse después de 2$\pi $. En efecto, dado que cualquier ángulo coterminal tendrá los mismos valores de seno y coseno, podríamos concluir que\[\sin (\theta +2\pi )=\sin (\theta )\nonumber\] y\[\cos (\theta +2\pi )=\cos (\theta )\nonumber\]

En otras palabras, si tuvieras que desplazar cualquiera de las gráficas horizontalmente por 2$\pi $, la forma resultante sería idéntica a la función original. Las funciones sinusoidales son un tipo específico de función periódica.

PERIODO DE SINO-SINO Y

Los periodos de las funciones seno y coseno son ambos 2$\pi $.

Mirar estas funciones en un dominio centrado en el eje vertical ayuda a revelar simetrías.

seno coseno

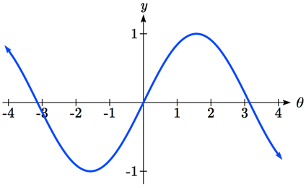
$Una gráfica sinusoidal centrada en el origen. En theta es igual a negativo 4 la gráfica está disminuyendo, pasando por pi coma 0 negativo y continuando hacia abajo a pi negativo sobre 2 comas negativo 1, luego girando y aumentando hasta el origen. Desde el origen sigue aumentando hacia arriba hasta pi sobre 2 comas 1, luego disminuye pasando por pi coma 0.$ $Una gráfica coseno centrada en el origen. En theta es igual a negativo 4 el gráfico está disminuyendo a negativo pi coma negativo 1, luego aumentando pasando por pi negativo sobre 2 coma 0 en el camino hasta 0 coma 1. La gráfica luego disminuye pasando por pi sobre 2 coma 0 en el camino hacia abajo a pi coma negativa 1, luego aumenta.$

La función seno es simétrica sobre el origen, la misma simetría que tiene la función cúbica, convirtiéndola en una función impar. La función coseno es claramente simétrica alrededor del eje y, la misma simetría que la función cuadrática, convirtiéndola en una función par.

Identidades de ángulo negativo

El seno es una función impar, simétrica sobre el origen, entonces\[\sin (-\theta )=-\sin (\theta )\]

El coseno es una función par, simétrica alrededor del eje y, por lo tanto\[\cos (-\theta )=\cos (\theta )\]

Estas identidades pueden ser utilizadas, entre otros fines, para ayudar a simplificar y probar identidades.

Puede recordar la identidad de la cofunción del último capítulo,\[\sin (\theta )=\cos \left(\dfrac{\pi }{2} -\theta \right)\nonumber\]

Gráficamente, esto nos dice que las gráficas de seno y coseno son transformaciones horizontales entre sí. Podemos probarlo usando la identidad de cofunción y la identidad de ángulo negativo para el coseno.

\[\sin (\theta )=\cos \left(\dfrac{\pi }{2} -\theta \right)=\cos \left(-\theta +\dfrac{\pi }{2} \right)=\cos \left(-\left(\theta -\dfrac{\pi }{2} \right)\right)=\cos \left(\theta -\dfrac{\pi }{2} \right)\]

Ahora podemos ver claramente que si desplazamos horizontalmente la función coseno hacia la derecha por$\pi $ /2 obtenemos la función sinusoidal.

Recuerde que este turno no representa el periodo de la función. Sólo muestra que la función coseno y seno son transformaciones entre sí.

Ejemplo$\PageIndex{1}$

Simplificar$\dfrac{\sin (-\theta )}{\tan (\theta )}$.

Solución

Comenzamos usando la identidad de ángulo negativo para seno.

\[\dfrac{-\sin (\theta )}{\tan (\theta )}\nonumber\]Reescribiendo la tangente
\[\dfrac{-\sin (\theta )}{\sin (\theta )/\cos(\theta)}\nonumber\] Invertiendo y multiplicando
\[-\sin (\theta )\cdot \dfrac{\cos (\theta )}{\sin (\theta )}\nonumber\] Simplificando obtenemos
\[-\cos (\theta )\nonumber\]

Transformación de Seno y Coseno

Ejemplo$\PageIndex{2}$

Un punto gira alrededor de un círculo de radio 3. Esboce una gráfica de la$y$ coordenada del punto.

Solución

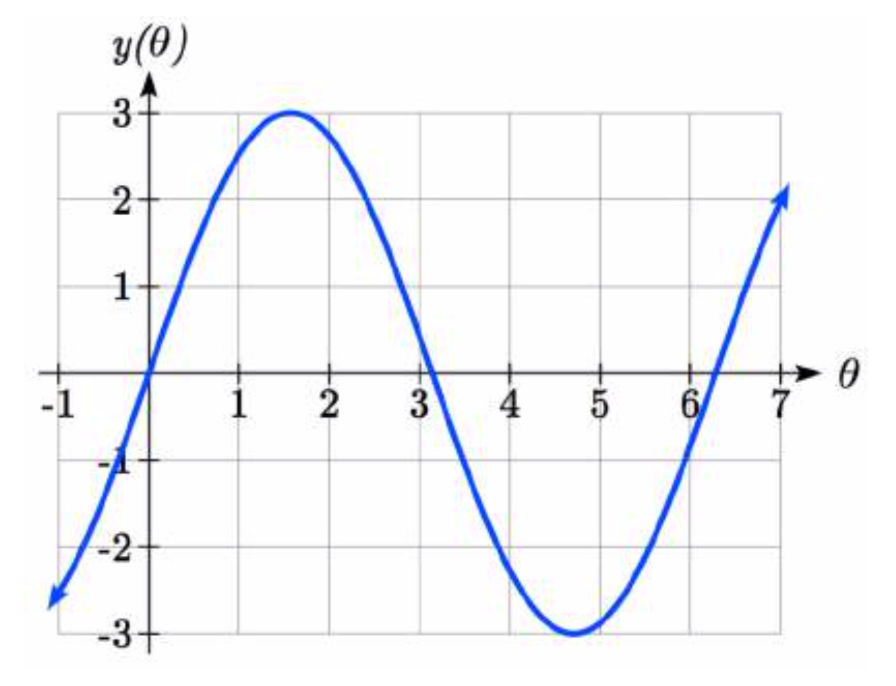
$Una gráfica sinusoidal. Desde el origen aumenta hasta el punto pi sobre 2 coma 3, luego disminuye, pasando por pi coma 0 y continuando disminuyendo a 3 pi sobre 2 coma negativa 3 antes de aumentar nuevamente, pasando por 2 pi coma 0$

Recordemos que para un punto en un círculo de radio$r$, la$y$ coordenada del punto es$y=r\sin (\theta )$, así que en este caso, obtenemos la ecuación\[y(\theta )=3\sin (\theta )\nonumber\]

La constante 3 provoca un estiramiento vertical de los$y$ valores de la función por un factor de 3.

Observe que el periodo de la función no cambia.

Dado que las salidas de la gráfica oscilarán ahora entre -3 y 3, decimos que la amplitud de la onda sinusoidal es 3.

Ejercicio$\PageIndex{1}$

¿Cuál es la amplitud de la función$f(\theta )=7\cos (\theta )$? Esboce una gráfica de esta función.

Contestar: 7

Ejemplo$\PageIndex{3}$

Un círculo con radio de 3 pies está montado con su centro a 4 pies del suelo. El punto más cercano al suelo está etiquetado$P$. Dibuja una gráfica de la altura sobre el suelo del punto a$P$ medida que se gira el círculo, luego encuentra una función que dé la altura en términos del ángulo de rotación.

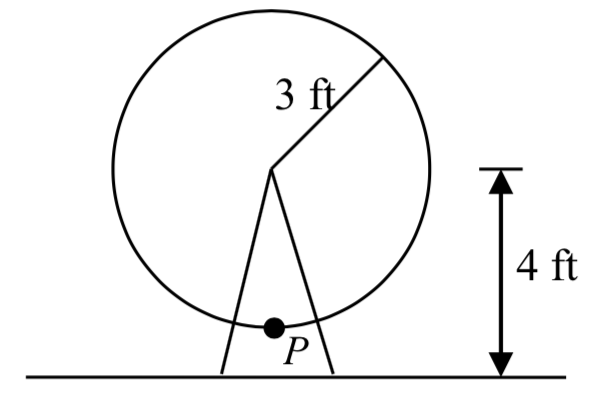
$Una imagen de un círculo con el centro a 4 pies del suelo. El círculo tiene radio 3. El punto más bajo en el círculo está etiquetado como P.$

Solución

Al esbozar la altura, observamos que comenzará a 1 pie sobre el suelo, luego aumentará hasta 7 pies sobre el suelo, y continuará oscilando 3 pies por encima y por debajo del valor central de 4 pies. 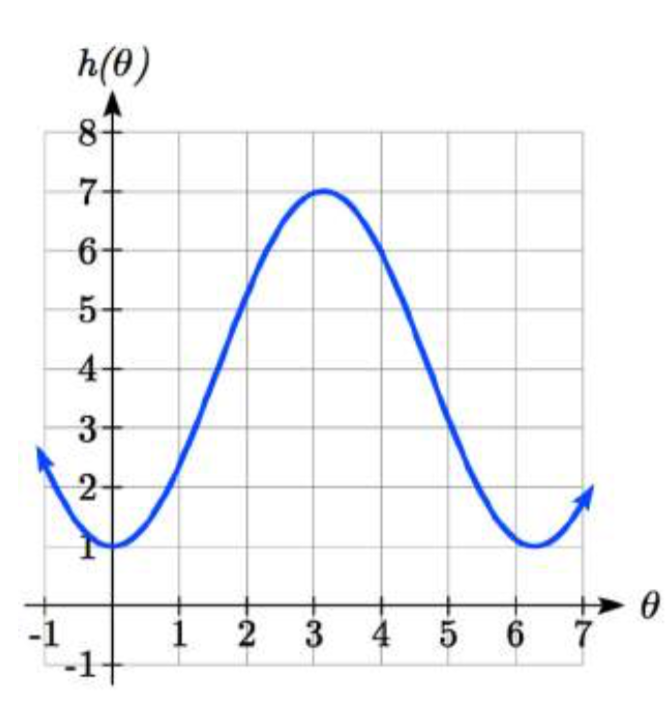$Una gráfica sinusoidal. En theta es igual a 0 la gráfica está en el valor más bajo 1. A medida que aumenta theta la gráfica aumenta hasta el punto pi coma 7, luego disminuye hasta 2 pi coma 1 antes de repetir.$

Aunque podríamos usar una transformación de la función sinusoidal o coseno, comenzamos por buscar características que hagan que una función sea más fácil de usar que la otra.

Decidimos usar una función coseno porque comienza en el valor más alto o más bajo, mientras que una función sinusoidal comienza en el valor medio. Un coseno estándar comienza en el valor más alto, y esta gráfica comienza en el valor más bajo, por lo que necesitamos incorporar una reflexión vertical.

Segundo, vemos que la gráfica oscila 3 por encima y por debajo del centro, mientras que un coseno básico tiene una amplitud de uno, por lo que esta gráfica ha sido estirada verticalmente en 3, como en el último ejemplo.

Finalmente, para mover el centro del círculo hasta una altura de 4, la gráfica se ha desplazado verticalmente hacia arriba en 4. Armando estas transformaciones,

\[h(\theta )=-3\cos (\theta )+4\nonumber\]

Definición: MIDLINE

El valor central de una función sinusoidal, el valor que la función oscila por encima y por debajo, se denomina la línea media de la función, correspondiente a un desplazamiento vertical.

La función$f(\theta )=\cos (\theta )+k$ tiene la línea media en$y = k$.

Ejercicio$\PageIndex{2}$

¿Cuál es la línea media de la función$f(\theta )=3\cos (\theta )-4$? Croquis de una gráfica de la función.

Contestar: -4

Para responder al problema de la noria al inicio de la sección, necesitamos poder expresar nuestras funciones seno y coseno en las entradas del tiempo. Para ello, utilizaremos composición. Dado que la función sinusoidal toma una entrada de un ángulo, buscaremos una función que tome tiempo como entrada y emita un ángulo. Si podemos encontrar una$\theta (t)$ función adecuada, entonces podemos componer esto con nuestra$f(\theta )=\cos (\theta )$ función para obtener una función sinusoidal del tiempo:$f(t)=\cos (\theta (t))$.

Ejemplo$\PageIndex{4}$

Un punto completa 1 revolución cada 2 minutos alrededor de un círculo de radio 5. Encuentra la$x$ coordenada del punto en función del tiempo, si comienza en (5, 0).

Solución

Normalmente, expresaríamos la$x$ coordenada de un punto en un círculo unitario usando$x=r\cos (\theta )$, aquí escribimos la función$x(\theta )=5\cos (\theta )$.

La velocidad de rotación de 1 revolución cada 2 minutos es una velocidad angular. Podemos usar esta tasa para encontrar una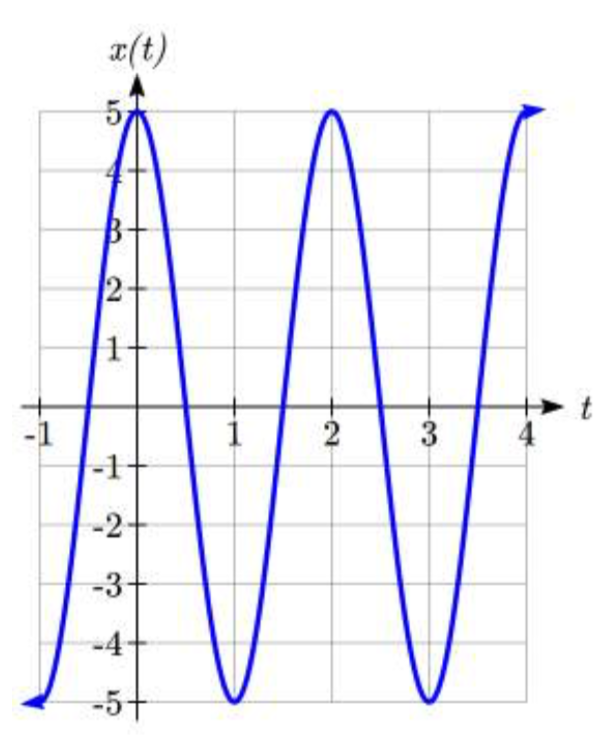 $Una gráfica sinusoidal etiquetada x de t. En t es igual a 0 la gráfica está en el valor más alto 5. Disminuye a 1 coma negativa 5, luego aumenta a 2 coma 5, luego disminuye a 3 coma negativa 5, luego aumenta nuevamente, repitiendo la oscilación.$ mula para el ángulo en función del tiempo. El punto comienza en un ángulo de 0. Dado que el punto gira 1 revolución = 2$\pi $ radianes cada 2 minutos, gira$\pi $ radianes cada minuto. Después de t minutos, habrá girado:

\[\theta (t)=\pi {\kern 1pt} t\text{ radians}\nonumber\]

Componiendo esto con la función coseno, obtenemos una función de tiempo.

\[x(t)=5\cos (\theta (t))=5\cos (\pi {\kern 1pt} t)\nonumber\]

Observe que esta composición tiene el efecto de una compresión horizontal, cambiando el periodo de la función.

Para ver cómo se relaciona el periodo con el coeficiente de estiramiento o compresión$B$ en la ecuación$f(t)=\sin \left(Bt\right)$, tenga en cuenta que el periodo será el tiempo que se tarda en completar una revolución completa de un círculo. Si un punto tarda$P$ minutos en completar 1 revolución, entonces la velocidad angular es$\dfrac{2\pi \; {\rm radians}}{P\; {\rm minutes}}$. Entonces$\theta (t)=\dfrac{2\pi }{P} t$. Componiendo con una función sinusoidal,

\[f(t)=\sin (\theta (t))=\sin \left(\dfrac{2\pi }{P} t\right)\nonumber\]

A partir de esto, podemos determinar la relación entre el coeficiente$B$ y el periodo:

\[B=\dfrac{2\pi }{P}\nonumber\]

Observe que el coeficiente de estiramiento o compresión$B$ es una relación entre el “período normal de una función sinusoidal” y el “nuevo período”. Si conocemos el coeficiente de estiramiento o compresión$B$, podemos resolver para el “nuevo periodo”:\[P=\dfrac{2\pi }{B}\nonumber\]

Resumiendo nuestras transformaciones hasta ahora:

TRANSFORMACIÓN DE SINO-SINOS

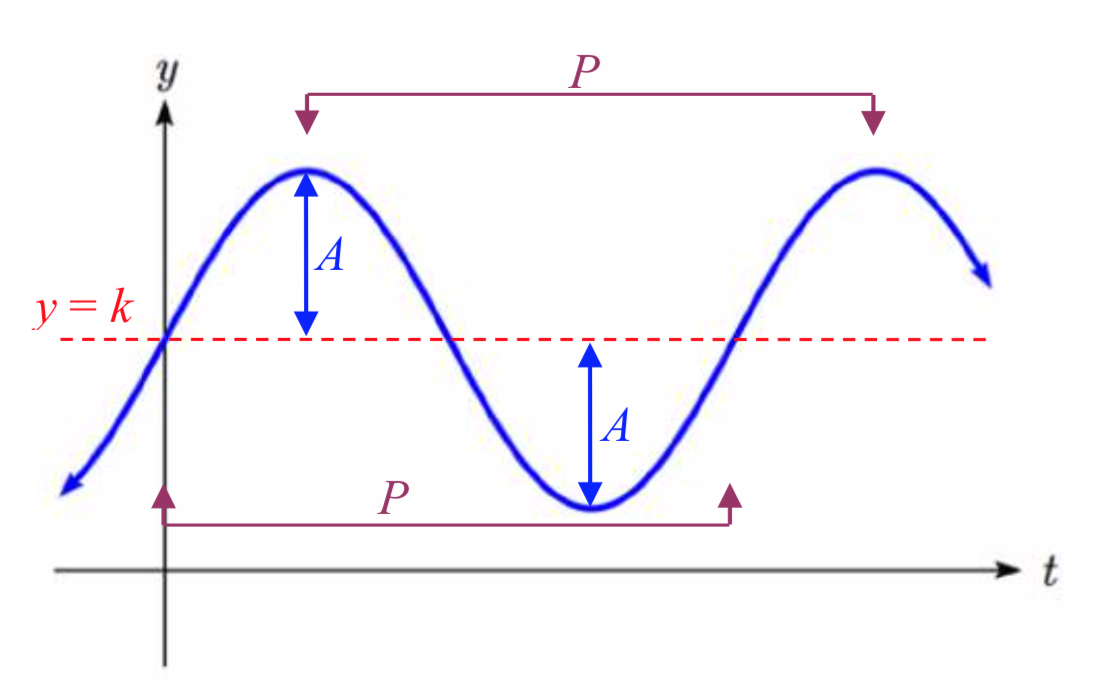
Dada una ecuación en la forma\[f(t)=A\sin \left(Bt\right)+k\text{ or }f(t)=A\cos \left(Bt\right)+k\]

$A$es el estiramiento vertical, y es la amplitud de la función.

$B$es el estiramiento/compresión horizontal, y está relacionado con el periodo,$P$, por$P=\dfrac{2\pi }{B}$.

$k$es el desplazamiento vertical y determina la línea media de la función.

$Una gráfica de una función sinusoidal transformada. Se muestra una línea discontinua horizontal pasando por el centro de la curva etiquetada como y es igual a k. La distancia desde la línea media hasta el punto más alto de la gráfica se etiqueta A. La distancia horizontal entre picos se etiqueta P. La distancia desde la línea media donde la gráfica está aumentando al siguiente lugar la gráfica cruza la línea media y la gráfica va en aumento también está etiquetada como P.$

Ejemplo$\PageIndex{5}$

¿Cuál es el periodo de la función$f(t)=\sin \left(\dfrac{\pi }{6} t\right)$?

Solución

Usando la relación anterior, el factor de estiramiento/compresión es$B=\dfrac{\pi }{6}$, por lo que el periodo será\[P=\dfrac{2\pi }{B} =\dfrac{2\pi }{\dfrac{\pi }{6} } =2\pi \cdot \dfrac{6}{\pi } =12\nonumber\]

Si bien es común componer seno o coseno con funciones que involucran tiempo, la composición se puede hacer para que la entrada represente cualquier cantidad razonable.

Ejemplo$\PageIndex{6}$

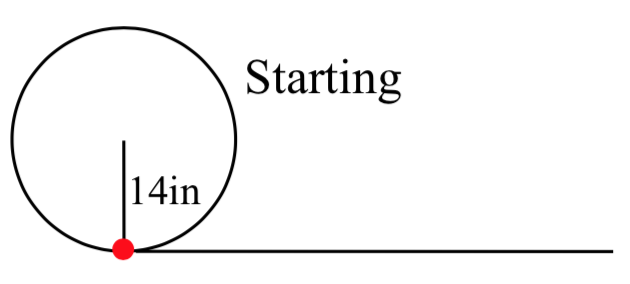
Una rueda de bicicleta con radio de 14 pulgadas tiene el punto más bajo de la rueda marcado en rojo. La rueda entonces comienza a rodar por la calle. Escribe una fórmula para la altura sobre el suelo del punto rojo después de que la bicicleta haya recorrido$x$ pulgadas.

$2019-07-09 3.22.25.png$

Solución

La altura del punto comienza en el valor más bajo, 0, aumenta al valor más alto de 28 pulgadas, y continúa oscilando por encima y por debajo de una altura central de 14 pulgadas. En términos del ángulo de rotación,$\theta$:

\[h(\theta )=-14\cos (\theta )+14\nonumber\]

En este caso,$x$ se representa una distancia lineal que ha recorrido la rueda, correspondiente a una longitud de arco a lo largo del círculo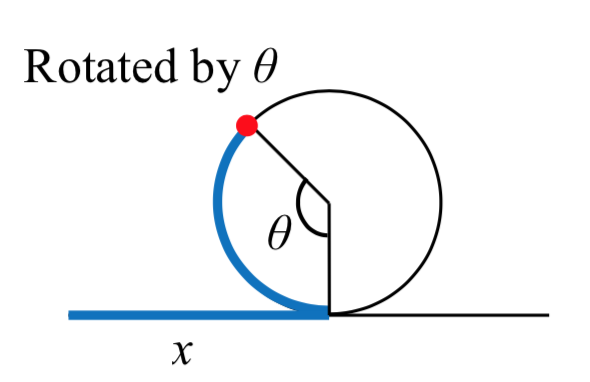 $2019-07-09 3.23.04.png$ . Dado que la longitud de arco y el ángulo se pueden relacionar por$s=r\theta$, en este caso podemos escribir$x=14\theta$, lo que nos permite expresar el ángulo en términos de$x$:

\[\theta (x)=\dfrac{x}{14}\nonumber\]

Componiendo esto con nuestra función basada en el coseno desde arriba,

\[h(x)=h(\theta (x))=-14\cos \left(\dfrac{x}{14} \right)+14=-14\cos \left(\dfrac{1}{14} x\right)+14\nonumber\]

El periodo de esta función sería$P=\dfrac{2\pi }{B} =\dfrac{2\pi }{\dfrac{1}{14} } =2\pi \cdot 14=28\pi$, la circunferencia del círculo. Esto tiene sentido: la rueda completa una revolución completa después de que la bicicleta haya recorrido una distancia equivalente a la circunferencia de la rueda.

Ejemplo$\PageIndex{7}$

Determinar la línea media, la amplitud y el período de la función$f(t)=3\sin \left(2t\right)+1$.

Solución

La amplitud es 3

El periodo es$P=\dfrac{2\pi }{B} =\dfrac{2\pi }{2} =\pi$

La línea media está en$y=1$

La amplitud, la línea media y el período, cuando se combinan con giros verticales, nos permiten escribir ecuaciones para una variedad de situaciones sinusoidales.

Ejercicio$\PageIndex{3}$

Si una función sinusoidal comienza en la línea media en el punto (0,3), tiene una amplitud de 2, y un período de 4, escriba una fórmula para la función.

Contestar: \[f(x)=2\sin \left(\dfrac{\pi }{2} x\right)+3\nonumber\]

Ejemplo$\PageIndex{8}$

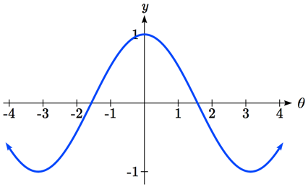
Encuentra una fórmula para la función sinusoidal graficada aquí.

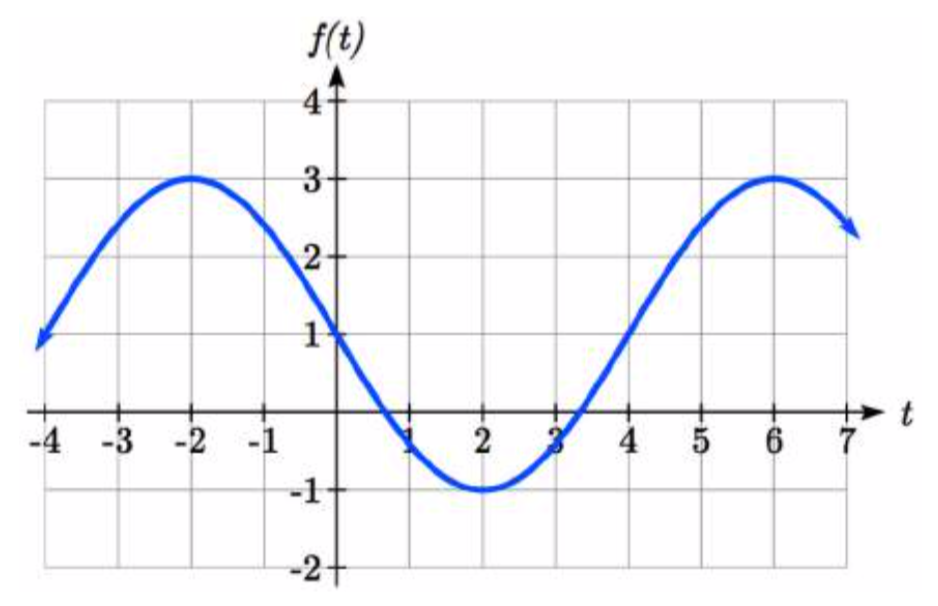
$Una gráfica sinusoidal. Desde la izquierda, entra en negativo 4 coma 1, aumenta a negativo 2 coma 3, disminuye a través de 0 coma 1 hasta 2 coma negativo 1, luego aumenta pasando por 4 coma 1 en el camino hasta 6 coma 3, luego disminuye saliendo de la ventana.$

Solución

El gráfico oscila de un mínimo de -1 a un máximo de 3, poniendo la línea media en$y = 1$, a medio camino entre.

La amplitud será 2, la distancia desde la línea media hasta el valor más alto (o valor más bajo) de la gráfica.

El periodo de la gráfica es 8. Podemos medir esto desde el primer pico en$x = -2$ hasta el segundo en$x = 6$. Dado que el periodo es 8, el factor de estiramiento/compresión que usaremos será

\[B=\dfrac{2\pi }{P} =\dfrac{2\pi }{8} =\dfrac{\pi }{4}\nonumber\]

At$x = 0$, la gráfica está en el valor de la línea media, lo que nos dice que la gráfica se puede representar más fácilmente como una función sinusoidal. Dado que la gráfica luego disminuye, ésta debe ser una reflexión vertical de la función sinusoidal. Poniendo todo esto junto,

\[f(t)=-2\sin \left(\dfrac{\pi }{4} t\right)+1\nonumber\]

Con estas transformaciones, estamos listos para responder al problema de la noria desde el inicio de la sección.

Ejemplo$\PageIndex{9}$

El London Eye es una enorme noria en Londres, Inglaterra, que completa una rotación cada 30 minutos. El diámetro de la rueda es de 120 metros, pero las cápsulas del pasajero se asientan fuera de la rueda. Supongamos que el diámetro en las cápsulas es de 130 metros, y los jinetes abordan desde una plataforma a 5 metros sobre el suelo. Exprese la altura de un ciclista sobre el suelo en función del tiempo en minutos.

Solución

A menudo puede ayudar a esbozar una gráfica de la situación antes de intentar encontrar la ecuación.

Con un diámetro de 130 metros, la rueda tiene un radio de 65 metros. La altura oscilará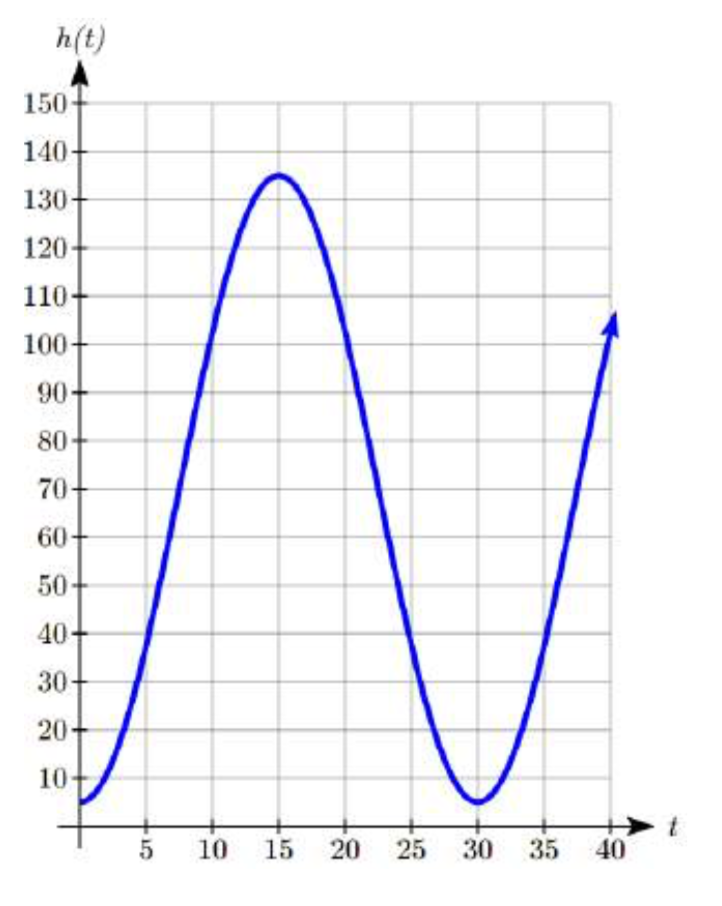 $Una gráfica sinusoidal, comenzando en el punto más bajo en 0 coma 5, aumentando a 15 coma 135, disminuyendo a 30 coma 5, luego aumentando nuevamente.$ con una amplitud de 65 metros por encima y por debajo del centro.

Los pasajeros abordan 5 metros sobre el nivel del suelo, por lo que el centro de la rueda debe estar ubicado 65 + 5 = 70 metros sobre el nivel del suelo. La línea media de la oscilación estará a 70 metros.

La rueda tarda 30 minutos en completar 1 revolución, por lo que la altura oscilará con un periodo de 30 minutos.

Por último, dado que el piloto sube en el punto más bajo, la altura comenzará en el valor más pequeño y aumentará, siguiendo la forma de una curva coseno volteada.

Armando estos:

Amplitud: 65

Línea media: 70

Periodo: 30, entonces\[B=\dfrac{2\pi }{30} =\dfrac{\pi }{15}\nonumber\]

Forma: coseno negativo

Una ecuación para la altura del piloto sería

\[h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70\nonumber\]

Ejercicio$\PageIndex{4}$

La noria en la Feria Puyallup (Foto de photogirl7.1, www.flickr.com/photos/kitkaph... 86205/talles/z/, CC-BY) ha $Una foto de una noria$ s un diámetro de unos 70 pies y tarda 3 minutos en completar una rotación completa. Los pasajeros suben desde una plataforma a 10 pies sobre el suelo. Escribe una ecuación para la altura de un piloto sobre el suelo a lo largo del tiempo.

Contestar: \[h(t)=-35\cos \left(\dfrac{2\pi }{3} t\right)+45\nonumber\]

Si bien estas transformaciones son suficientes para representar muchas situaciones, ocasionalmente nos encontramos con una función sinusoidal que no tiene una intercepción vertical en el punto más bajo, punto más alto o línea media. En estos casos, necesitamos usar turnos horizontales. Ya que estamos combinando desplazamientos horizontales con estiramientos horizontales, debemos tener cuidado. Recordemos que cuando se factoriza el interior de la función, revela el desplazamiento horizontal.

DESVIOS HORIZONTALES DE SINO

Dada una ecuación en la forma\[f(t)=A\sin \left(B(t-h)\right)+k\text{ or }f(t)=A\cos \left(B(t-h)\right)+k\]

$h$es el desplazamiento horizontal de la función

Ejemplo$\PageIndex{10}$

Esbozar una gráfica de$f(t)=3\sin \left(\dfrac{\pi }{4} t-\dfrac{\pi }{4} \right)$.

Solución

Para revelar el desplazamiento horizontal, primero necesitamos factorizar dentro de la función:

\[f(t)=3\sin \left(\dfrac{\pi }{4} (t-1)\right)\nonumber\]

Esta gráfica tendrá la forma de una función sinusoidal, comenzando en la línea media y aumentando, con una amplitud de 3. El periodo de la gráfica será\[P=\dfrac{2\pi }{B} =\dfrac{2\pi }{\dfrac{\pi }{4} } =2\pi \cdot \dfrac{4}{\pi } =8\nonumber\]

Por último, la gráfica se desplazará a la derecha en 1.

$Una gráfica sinusoidal. Desde un punto más bajo en negativo 1 coma negativo 3 aumenta, pasando por 1 coma 0 en el camino a 3 coma 3, luego disminuye pasando por 5 coma 0 en el camino a 7 coma negativa 3, luego aumentando nuevamente por 9 coma 0 antes de salir de la ventana.$

En algunos libros de física y matemáticas, escucharás el cambio horizontal denominado desplazamiento de fase. En otros libros de física y matemáticas, dirían que el desplazamiento de fase de la ecuación anterior es$\dfrac{\pi }{4}$, el valor en la forma no factorizada. Debido a esta ambigüedad, no vamos a utilizar más el término desplazamiento de fase, y sólo hablaremos del cambio horizontal.

Ejemplo$\PageIndex{11}$

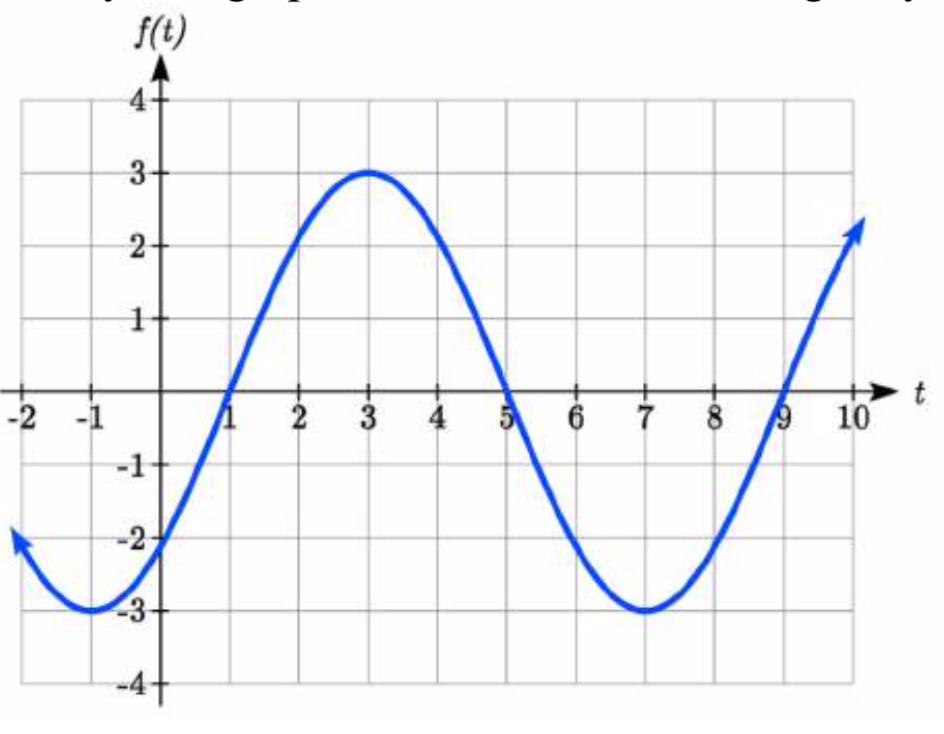
Encuentra una fórmula para la función graficada aquí.

$Una gráfica sinusoidal. Desde un punto más bajo en negativo 2 coma negativo 5 aumenta hasta 1 coma 1, luego disminuye hasta 4 coma negativa 5, luego aumenta nuevamente hasta 7 coma 1, luego disminuye antes de salir de la ventana.$

Solución

Con el valor más alto en 1 y el valor más bajo en -5, la línea media estará a medio camino entre en -2.

La distancia desde la línea media hasta el valor más alto o más bajo da una amplitud de 3.

El periodo de la gráfica es 6, que se puede medir desde el pico en$x = 1$ hasta el siguiente pico en$x = 7$, o desde la distancia entre los puntos más bajos. Esto da\[B=\dfrac{2\pi }{P} =\dfrac{2\pi }{6} =\dfrac{\pi }{3}\nonumber\]

Para la forma y el turno, tenemos más de una opción. Podríamos escribir esto como:

Un coseno se desplazó 1 a la derecha

Un coseno negativo se desplazó 2 a la izquierda

Un seno desplazado 1/2 a la izquierda

Un seno negativo desplazado 2.5 a la derecha

Si bien cualquiera de estos estaría bien, los desplazamientos coseno son más fáciles de trabajar que los cambios sinusoidales en este caso, porque involucran valores enteros. Escribiendo estos:

\[y(x)=3\cos \left(\dfrac{\pi }{3} (x-1)\right)-2\nonumber\]o
\[y(x)=-3\cos \left(\dfrac{\pi }{3} (x+2)\right)-2\nonumber\]

Nuevamente, estas funciones son equivalentes, por lo que ambas producen la misma gráfica.

Ejercicio$\PageIndex{5}$

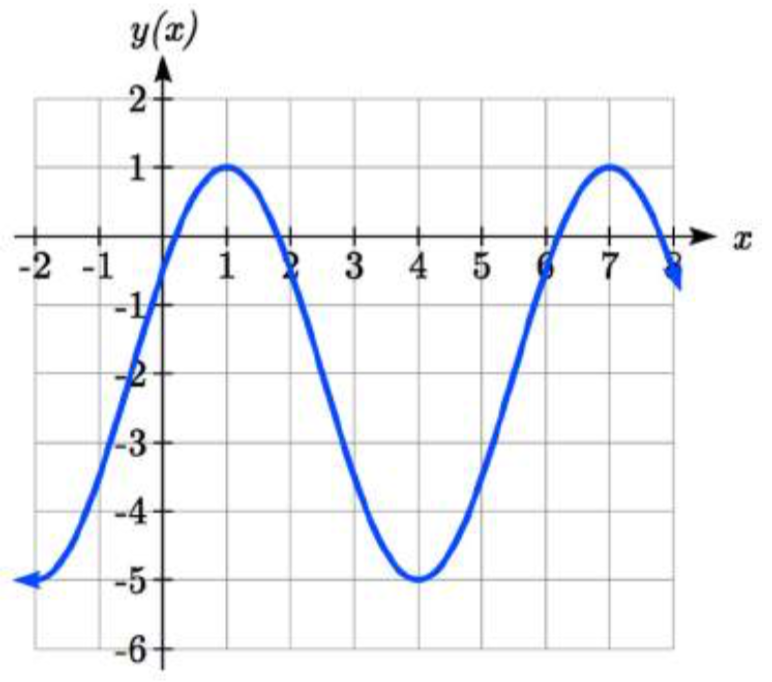
Escribe una fórmula para la función graficada aquí. 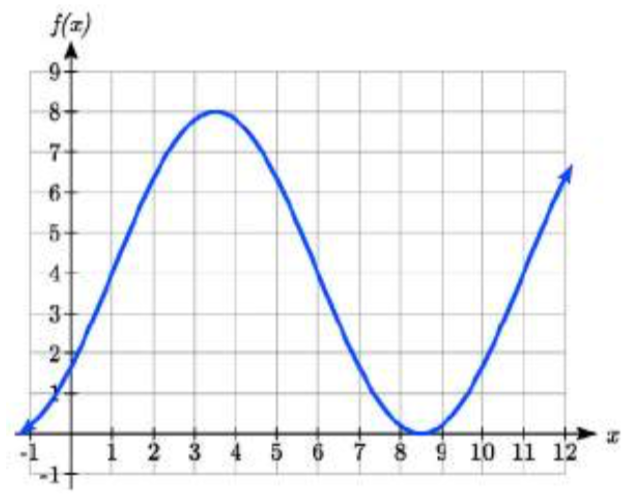$Una gráfica sinusoidal. Entra en la ventana aumentando, pasando por 1 coma 4 en el camino hasta el punto más alto alrededor de 3.5 coma 8, luego disminuye pasando por 6 coma 4 en el camino hacia abajo a 8.5 coma 0, luego vuelve a aumentar pasando por 11 coma 4 antes de salir de la ventana.$

Contestar: Dos posibilidades:\[f(x)=4\cos \left(\dfrac{\pi }{5} (x-3.5)\right)+4\text{ or }f(x)=4\sin \left(\dfrac{\pi }{5} (x-1)\right)+4\nonumber\]

Temas Importantes de esta Sección

Funciones periódicas
Función sinusoidal y coseno del círculo unitario
Dominio y rango de funciones sinusoidales y cosenales
Funciones sinusoidales
Identidad de ángulo negativo
Simplificar expresiones
Transformaciones
Amplitud
Línea media
Periodo
Turnos horizontales

*\(\theta\)*	0	\(\dfrac{\pi }{6}\)	\(\dfrac{\pi }{4}\)	\(\dfrac{\pi }{3}\)	\(\dfrac{\pi }{2}\)	\(\dfrac{2\pi }{3}\)	\(\dfrac{3\pi }{4}\)	\(\dfrac{5\pi }{6}\)	\(\pi\)
cos	1	\(\dfrac{\sqrt{3} }{2}\)	\(\dfrac{\sqrt{2} }{2}\)	\(\dfrac{1}{2}\)	0	\(-\dfrac{1}{2}\)	\(-\dfrac{\sqrt{2} }{2}\)	\(-\dfrac{\sqrt{3} }{2}\)	-1
pecado	0	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2} }{2}\)	\(\dfrac{\sqrt{3} }{2}\)	1	\(\dfrac{\sqrt{3} }{2}\)	\(\dfrac{\sqrt{2} }{2}\)	\(\dfrac{1}{2}\)	0