6.3: Funciones trigonométricas inversas

Última actualización
Guardar como PDF

Page ID: 116670

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En secciones anteriores, hemos evaluado las funciones trigonométricas en varios ángulos, pero a veces necesitamos saber qué ángulo produciría un valor específico de seno, coseno o tangente. Para ello, necesitamos funciones inversas. Recordemos que para una función uno a uno, si$f(a)=b$, entonces una función inversa satisfacería$f^{-1} (b)=a$.

Probablemente ya estés reconociendo un problema —que las funciones seno, coseno y tangente no son funciones uno a uno. Para definir una inversa de estas funciones, necesitaremos restringir el dominio de estas funciones para producir una nueva función que sea uno a uno. Elegimos un dominio para cada función que incluya el ángulo cero.

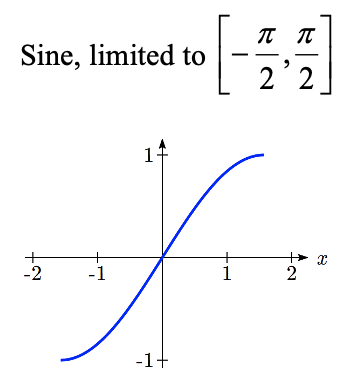
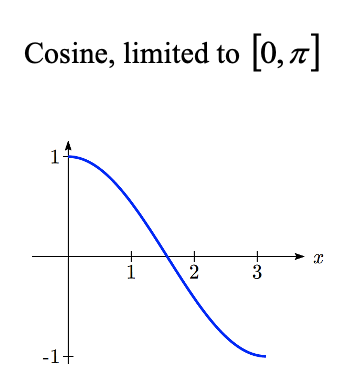
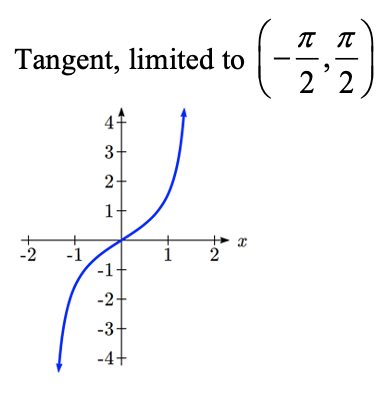
$Una porción de la gráfica sinusoidal. Esta porción comienza en pi negativo sobre 2 coma negativa 1, aumenta cóncava hasta el origen, luego aumenta cóncava hacia abajo a pi sobre 1 coma 1.$ $Una porción de la gráfica coseno. Esta porción comienza en 0 coma 1, disminuye cóncava abajo a pi sobre 2 coma 0, luego disminuye cóncava hasta pi coma negativa 1.$ $Una porción de la gráfica tangente. Esta porción es un segmento creciente, que se acerca al infinito negativo a medida que x se acerca a pi negativo sobre 2 desde la derecha, y aumenta cóncavo hacia abajo hasta el origen, luego aumenta cóncava hacia arriba, acercándose al infinito a medida que x se acerca a pi sobre 2 desde la izquierda.$

En estos dominios restringidos, podemos definir las funciones seno inverso, coseno inverso y tangente inversa.

FUNCIONES INVERSAS DE SINO, COSINO Y TANGENTE y sus inversas

Para ángulos en el intervalo$\left[-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right]$, si$\sin \left(\theta \right)=a$, entonces$\sin ^{-1} \left(a\right)=\theta$

$\sin ^{-1} \left(x\right)$tiene dominio [-1, 1] y rango$\left[-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right]$

A veces$\sin ^{-1} \left(x\right)$ se le llama la función arcoseno, y se anota$\arcsin \left(a\right)$.

Para ángulos en el intervalo$\left[0,\pi \right]$, si$\cos \left(\theta \right)=a$, entonces$\cos ^{-1} \left(a\right)=\theta$

$\cos ^{-1} \left(x\right)$tiene dominio [-1, 1] y rango$\left[0,\pi \right]$

El a veces$\cos ^{-1} \left(x\right)$ se llama la función arccosina, y anotado$\arccos \left(a\right)$.

Para ángulos en el intervalo$\left(-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right)$, si$\tan \left(\theta \right)=a$, entonces$\tan ^{-1} \left(a\right)=\theta$

$\tan ^{-1} \left(x\right)$tiene dominio de todos los números reales y rango$\left(-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right)$

El a veces$\tan ^{-1} \left(x\right)$ se llama la función arcotangente, y se nota$\arctan \left(a\right)$.

Las gráficas de las funciones inversas se muestran aquí:

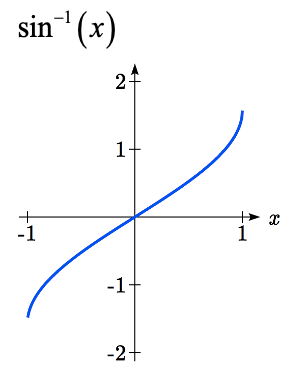
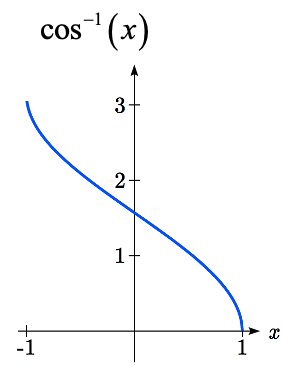
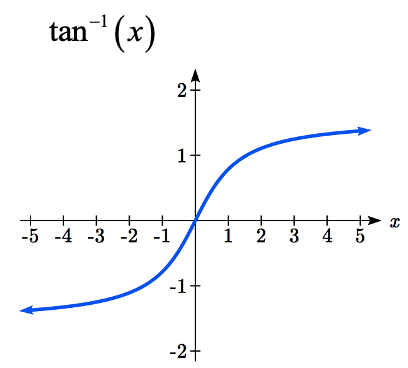
$La gráfica de la función sinusoidal inversa. Comienza en negativo 1 coma negativo pi sobre 2, aumenta cóncavo hasta el origen, luego aumenta cóncavo hasta 1 coma pi sobre 2.$ $La gráfica de la función inversa del coseno. Comienza en negativo 1 coma pi, disminuye cóncava hasta 0 coma pi sobre 2, luego disminuye cóncava hasta 1 coma 0.$ $Una gráfica de la función inversa tangente. Comienza justo por encima de una asíntota horizontal en pi negativo sobre 2, aumentando cóncava hasta el origen, luego aumenta cóncava hacia abajo y nivelando en otra asíntota horizontal en pi sobre 2.$

Observe que la salida de cada una de estas funciones inversas es una$angle$.

Ejemplo$\PageIndex{1}$

Evaluar

$\sin ^{-1} \left(\dfrac{1}{2} \right)$
$\sin ^{-1} \left(-\dfrac{\sqrt{2} }{2} \right)$
$\cos ^{-1} \left(-\dfrac{\sqrt{3} }{2} \right)$
$\tan ^{-1} \left(1\right)$

Solución

a) Evaluar$\sin ^{-1} \left(\dfrac{1}{2} \right)$ es lo mismo que preguntar qué ángulo tendría un valor sinusoidal de$\dfrac{1}{2}$. En otras palabras, ¿qué ángulo $\theta$satisfaría$\sin \left(\theta \right)=\dfrac{1}{2}$?

Hay múltiples ángulos que satisfarían esta relación, como$\dfrac{\pi }{6}$ y$\dfrac{5\pi }{6}$, pero sabemos que necesitamos el ángulo en el rango de$\sin ^{-1} \left(x\right)$, el intervalo$\left[-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right]$, entonces la respuesta será\[\sin ^{-1} \left(\dfrac{1}{2} \right)=\dfrac{\pi }{6}\nonumber\]

Recuerda que la inversa es una función así que para cada entrada, obtendremos exactamente una salida.

b) Evaluando$\sin ^{-1} \left(-\dfrac{\sqrt{2} }{2} \right)$, sabemos que$\dfrac{5\pi }{4}$ y$\dfrac{7\pi }{4}$ ambos tienen un valor sinusoidal de$-\dfrac{\sqrt{2} }{2}$, pero ninguno está en el intervalo$\left[-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right]$. Para ello, necesitamos el ángulo negativo coterminal con$\dfrac{7\pi }{4}$. \[\sin ^{-1} \left(-\dfrac{\sqrt{2} }{2} \right)=-\dfrac{\pi }{4}\nonumber\]

c) Evaluando$\cos ^{-1} \left(-\dfrac{\sqrt{3} }{2} \right)$, estamos buscando un ángulo en el intervalo$\left[0,\pi \right]$ con un valor coseno de$-\dfrac{\sqrt{3} }{2}$. El ángulo que satisface esto es\[\cos ^{-1} \left(-\dfrac{\sqrt{3} }{2} \right)=\dfrac{5\pi }{6}\nonumber\]

d) Evaluando$\tan ^{-1} \left(1\right)$, estamos buscando un ángulo en el intervalo$\left(-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right)$ con un valor tangente de 1. El ángulo correcto es\[\tan ^{-1} \left(1\right)=\dfrac{\pi }{4}\nonumber\]

Ejercicio$\PageIndex{1}$

Evaluar

$\sin ^{-1} \left(-1\right)$
$\tan ^{-1} \left(-1\right)$
$\cos ^{-1} \left(-1\right)$
$\cos ^{-1} \left(\dfrac{1}{2} \right)$

Contestar

a)$-\dfrac{\pi }{2}$

b)$-\dfrac{\pi }{4}$

c)$\pi$

d)$\dfrac{\pi }{3}$

Ejemplo$\PageIndex{2}$

Evalúa$\sin ^{-1} \left(0.97\right)$ usando tu calculadora.

Solución

Dado que la salida de la función inversa es un ángulo, su calculadora le dará un valor de grado si está en modo grado, y un valor de radianes si está en modo radián.

En modo radián,\[\sin ^{-1} (0.97) \approx 1.3252\nonumber\]

En modo grado,\[\sin ^{-1} \left(0.97\right)\approx 75.93{}^\circ\nonumber\]

Ejercicio

Evalúa$\cos ^{-1} \left(-0.4\right)$ usando tu calculadora.

Contestar: \[1.9823\text{ or }113.578\mathrm{{}^\circ}\nonumber\]

En la Sección 5.5, se trabajó con trigonometría en un triángulo rectángulo para resolver los lados de un triángulo dado un lado y un ángulo adicional. Usando las funciones trigonométricas inversas, podemos resolver los ángulos de un triángulo rectángulo dados dos lados.

Ejemplo$\PageIndex{3}$

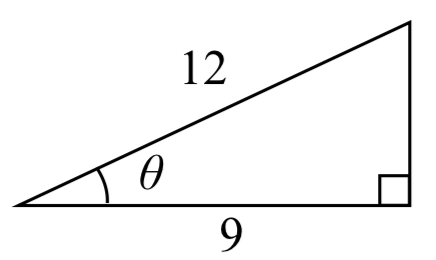
Resuelve el triángulo para el ángulo$\theta$.

$Un triángulo rectángulo con hipotenusa etiquetada 12 y una cara etiquetada con 9, y el ángulo entre ellas etiquetada theta.$

Solución

Como conocemos la hipotenusa y el lado adyacente al ángulo, tiene sentido que usemos la función coseno.

\[\cos \left(\theta \right)=\dfrac{9}{12}\nonumber\]Usando la definición de la inversa,

\[\theta =\cos ^{-1} \left(\dfrac{9}{12} \right)\nonumber\]Evaluando

\[\theta \approx 0.7227\text{, or about }41.4096\mathrm{{}^\circ}\nonumber\]

Hay momentos en los que necesitamos componer una función trigonométrica con una función trigonométrica inversa. En estos casos, podemos encontrar valores exactos para las expresiones resultantes

Ejemplo$\PageIndex{4}$

Evaluar$\sin ^{-1} \left(\cos \left(\dfrac{13\pi }{6} \right)\right)$.

Solución

a) Aquí, podemos evaluar directamente el interior de la composición.

\[\cos \left(\dfrac{13\pi }{6} \right)=\dfrac{\sqrt{3} }{2}\nonumber\]

Ahora, podemos evaluar la función inversa como hicimos antes.

\[\sin ^{-1} \left(\dfrac{\sqrt{3} }{2} \right)=\dfrac{\pi }{3}\nonumber\]

Ejercicio$\PageIndex{3}$

Evaluar$\cos ^{-1} \left(\sin \left(-\dfrac{11\pi }{4} \right)\right)$.

Contestar: \[\sin \left(-\dfrac{11\pi }{4} \right)=-\dfrac{\sqrt{2} }{2} . \cos ^{-1} \left(-\dfrac{\sqrt{2} }{2} \right)=\dfrac{3\pi }{4} \nonumber\]

Ejemplo$\PageIndex{5}$

Encuentra un valor exacto para$\sin \left(\cos ^{-1} \left(\dfrac{4}{5} \right)\right)$.

Solución

Comenzando por el interior, podemos decir que hay algún ángulo así$\theta =\cos ^{-1} \left(\dfrac{4}{5} \right)$, lo que significa$\cos \left(\theta \right)=\dfrac{4}{5}$, y estamos buscando$\sin \left(\theta \right)$. Podemos usar la identidad pitagórica para hacer esto.

\[\sin ^{2} \left(\theta \right)+\cos ^{2} \left(\theta \right)=1\nonumber\]Usando nuestro valor conocido para la
\[\sin ^{2} \left(\theta \right)+\left(\dfrac{4}{5} \right)^{2} =1\nonumber\] resolución de coseno para seno
\[\sin ^{2} \left(\theta \right)=1-\dfrac{16}{25}\nonumber\]
\[\sin \left(\theta \right)=\pm \sqrt{\dfrac{9}{25} } =\pm \dfrac{3}{5}\nonumber\]

Como sabemos que el coseno inverso siempre da un ángulo en el intervalo$\left[0,\pi \right]$, sabemos que el seno de ese ángulo debe ser positivo, entonces\[\sin \left(\cos ^{-1} \left(\dfrac{4}{5} \right)\right)=\sin (\theta )=\dfrac{3}{5}\nonumber\]

Ejemplo$\PageIndex{6}$

Encuentra un valor exacto para$\sin \left(\tan ^{-1} \left(\dfrac{7}{4} \right)\right)$.

Solución

Si bien podríamos usar una te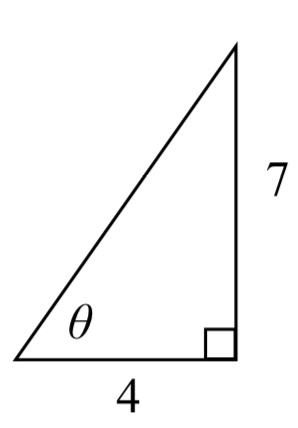 $Un triángulo rectángulo con patas 4 y 7. La longitud lateral 4 se encuentra con la hipotenusa en un ángulo etiquetado theta.$ chnique similar como en el último ejemplo, aquí demostraremos una técnica diferente. Desde adentro, sabemos que hay un ángulo así$\tan \left(\theta \right)=\dfrac{7}{4}$. Podemos imaginar esto como los lados opuestos y adyacentes en un triángulo rectángulo.

Utilizando el Teorema de Pitágoras, podemos encontrar la hipotenusa de este triángulo:

\[4^{2} +7^{2} =hypotenuse ^{2}\nonumber\]

\[hypotenuse=\sqrt{65}\nonumber\]

Ahora, podemos representar el seno del ángulo como lado opuesto dividido por hipotenusa.

\[\sin \left(\theta \right)=\dfrac{7}{\sqrt{65} }\nonumber\]

Esto nos da nuestra composición deseada

\[\sin \left(\tan ^{-1} \left(\dfrac{7}{4} \right)\right)=\sin (\theta )=\dfrac{7}{\sqrt{65} } .\nonumber\]

Ejercicio$\PageIndex{4}$

Evaluar$\cos \left(\sin ^{-1} \left(\dfrac{7}{9} \right)\right)$.

Contestar

Que$\theta =\sin ^{-1} \left(\dfrac{7}{9} \right)$ así\[\sin (\theta )=\dfrac{7}{9}\nonumber\]

Usando Identidad Pitagórica,$\sin ^{2} \theta +\cos ^{2} \theta =1$, entonces\[\left(\dfrac{7}{9} \right)^{2} +\cos ^{2} \theta =1\nonumber\]

Resolviendo,\[\cos \left(\sin ^{-1} \left(\dfrac{7}{9} \right)\right)=\cos \left(\theta \right)=\dfrac{4\sqrt{2} }{9}\nonumber\]

También podemos encontrar composiciones que involucran expresiones algebraicas

Ejemplo$\PageIndex{7}$

Encuentra una expresión simplificada para$\cos \left(\sin ^{-1} \left(\dfrac{x}{3} \right)\right)$, para$-3\le x\le 3$.

Solución

Sabemos que hay un ángulo $\theta$para que$\sin \left(\theta \right)=\dfrac{x}{3}$. Usando el Teorema de Pitágoras,

\[\sin ^{2} \left(\theta \right)+\cos ^{2} \left(\theta \right)=1\nonumber\]Usando nuestra expresión conocida para la
\[\left(\dfrac{x}{3} \right)^{2} +\cos ^{2} \left(\theta \right)=1\nonumber\] resolución de seno para coseno
\[\cos ^{2} \left(\theta \right)=1-\dfrac{x^{2} }{9}\nonumber\]
\[\cos \left(\theta \right)=\pm \sqrt{\dfrac{9-x^{2} }{9} } =\pm \dfrac{\sqrt{9-x^{2} } }{3}\nonumber\]

Ya que sabemos que el seno inverso debe dar un ángulo en el intervalo$\left[-\dfrac{\pi }{2} ,\dfrac{\pi }{2} \right]$, podemos deducir que el coseno de ese ángulo debe ser positivo. Esto nos da

\[\cos \left(\sin ^{-1} \left(\dfrac{x}{3} \right)\right)=\dfrac{\sqrt{9-x^{2} } }{3}\nonumber\]

Ejercicio$\PageIndex{5}$

Encuentra una expresión simplificada para$\sin \left(\tan ^{-1} \left(4x\right)\right)$, para$-\dfrac{1}{4} \le x\le \dfrac{1}{4}$.

Contestar

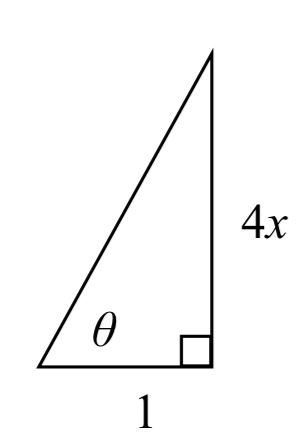
Vamos$\theta =\tan ^{-1} \left(4x\right)$, entonces$\tan (\theta )=4x$. Podemos representar esto en un triángulo como$\tan (\theta )=\dfrac{4x}{1}$. $Un triángulo rectángulo con un ángulo etiquetado theta, y la pata opuesta etiquetada 4x y la pata adyacente etiquetada con 1.$

La hipotenusa del triángulo sería$\sqrt{\left(4x\right)^{2} +1}$. \[\sin \left(\tan ^{-1} \left(4x\right)\right)=\sin (\theta )=\dfrac{4x}{\sqrt{16x^{2} +1} }\nonumber\]

Temas Importantes de esta Sección

Funciones trigonométricas inversas: arcoseno, arcoseno y arcotangente
Restricciones de dominio
Evaluar las inversas usando valores de círculo unitario y la calculadora
Simplificar expresiones numéricas que involucran las funciones trigonométricas inversas
Simplificar expresiones algebraicas que involucran las funciones trigonométricas inversas