6.4: Resolver ecuaciones trigonométricas

Última actualización
Guardar como PDF

Page ID: 116704

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 6.1, determinamos que la altura de un piloto en la noria London Eye podría ser determinada por la ecuación

\[h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70. \nonumber\]

Si quisiéramos saber el tiempo durante el cual el piloto se encuentra a más de 100 metros sobre el suelo, necesitaríamos resolver ecuaciones que involucren funciones trig.

Resolver usando Valores Conocidos

En el último capítulo aprendimos valores de seno y coseno en ángulos comúnmente encontrados. Podemos usar estos para resolver ecuaciones de seno y coseno que involucran estos ángulos comunes.

Ejemplo$\PageIndex{1}$

Resolver$\sin \left(t\right)=\dfrac{1}{2}$ para todos los valores posibles de$t$.

Solución

Observe esto nos está pidiendo que identifiquemos todos los ángulos$t$,, que tengan un valor sinusoidal de$\dfrac{1}{2}$. Si bien la evaluación de una función siempre produce un resultado, la resolución de una entrada puede producir múltiples soluciones. Dos soluciones deben saltar inmediatamente a la mente desde el último capítulo:$t=\dfrac{\pi }{6}$ y$t=\dfrac{5\pi }{6}$ porque son los ángulos comunes en el círculo unitario con un pecado de$\dfrac{1}{2}$.

Mirar una gráfica confirma que hay más de estas dos soluciones. Si bien se ven ocho en esta gráfica, ¡hay un número infinito de soluciones!

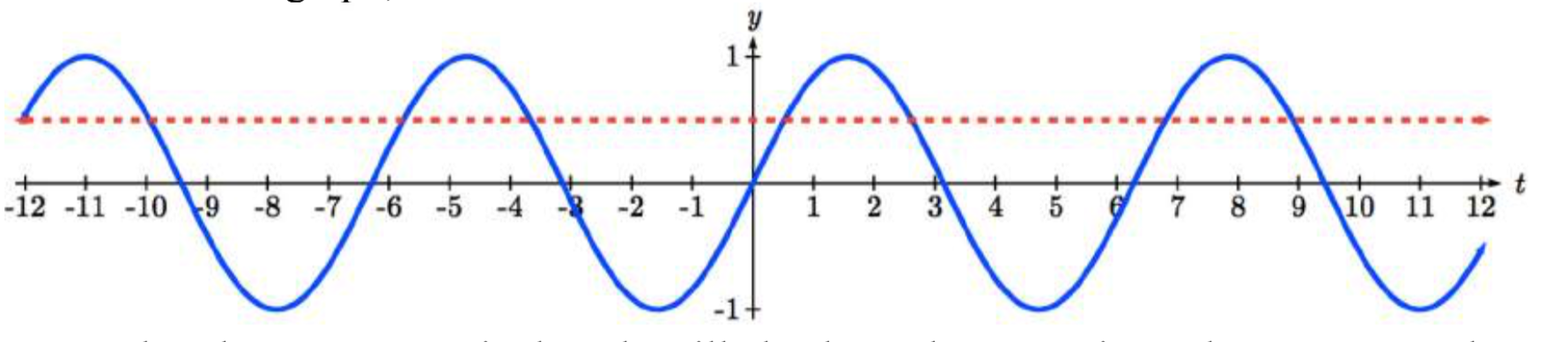
$Una gráfica de seno de t, para valores de t de 12 a 12 negativos, y una línea horizontal a la mitad. La línea horizontal cruza la gráfica sinusoidal en 8 ubicaciones en la ventana mostrada.$

Recuerde que cualquier ángulo coterminal también tendrá el mismo valor sinusoidal, por lo que cualquier ángulo coterminal con estas nuestras dos primeras soluciones también es una solución. Los ángulos coterminales se pueden encontrar agregando rotaciones completas de 2$\pi $, para que podamos escribir el conjunto completo de soluciones:

$t=\dfrac{\pi }{6} +2\pi k$donde k es un entero, y$t=\dfrac{5\pi }{6} +2\pi k$ donde$k$ es un entero.

Ejemplo$\PageIndex{2}$

Un círculo de radio$5\sqrt{2}$ cruza la línea$x = -5$ en dos puntos. Encuentra los ángulos$\theta$ en el intervalo$0 \le \theta <2\pi$, donde se cruzan el círculo y la línea.

Solución

La$x$ coordenada de un punto en un círculo se puede encontrar como$x=r\cos \left(\theta \right)$, por lo que la$x$ coordenada de puntos en este círculo sería$x=5\sqrt{2} \cos \left(\theta \right)$. Para encontrar dónde la línea$x = -5$ se cruza con el círculo, podemos resolver por dónde el$x$ valor en el círculo sería -5.

\[-5=5\sqrt{2} \cos \left(\theta \right)\nonumber\]Aislar el coseno

\[\dfrac{-1}{\sqrt{2} } =\cos \left(\theta \right)\nonumber\]Recordemos eso$\dfrac{-1}{\sqrt{2} } =\dfrac{-\sqrt{2} }{2}$, así estamos resolviendo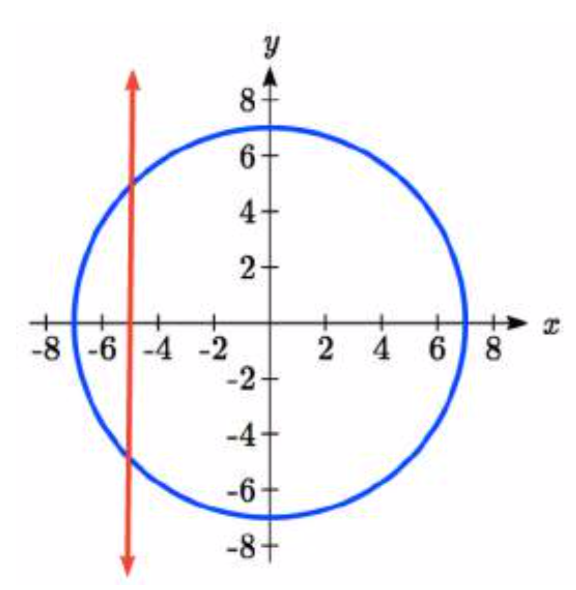 $Un círculo con radio 7 centrado en el origen, y una línea vertical en x es igual a 5 negativo, que cruza el círculo en dos puntos.$

\[\cos \left(\theta \right)=\dfrac{-\sqrt{2} }{2}\nonumber\]

Podemos reconocer esto como uno de nuestros valores coseno especiales de nuestro círculo unitario, y corresponde con ángulos\[\theta =\dfrac{3\pi }{4}\text{ and }\theta =\dfrac{5\pi }{4}\nonumber\]

Ejercicio$\PageIndex{1}$

Resolver$\tan \left(t\right)=1$ para todos los valores posibles de$t$.

Contestar: Desde nuestros ángulos especiales, sabemos que una respuesta es$t=\dfrac{\pi }{4}$. Las ecuaciones tangentes solo tienen una solución única por ciclo o período, por lo que se pueden encontrar soluciones adicionales agregando múltiplos de un período completo,$\pi $. \[t=\dfrac{\pi }{4} +\pi k\nonumber\]

Ejemplo$\PageIndex{3}$

La profundidad del agua en un muelle sube y baja con la marea, siguiendo la ecuación$f(t)=4\sin \left(\dfrac{\pi }{12} t\right)+7$, donde t se mide en horas posteriores a la medianoche. Un bote requiere una profundidad de 9 pies para amarrarse en el muelle. ¿Entre qué tiempos será la profundidad de 9 pies?

Solución

Para encontrar cuando la profundidad es de 9 pies, necesitamos resolverlo$f(t) = 9$.

\[4\sin \left(\dfrac{\pi }{12} t\right)+7=9\nonumber\]Aislar el seno
\[4\sin \left(\dfrac{\pi }{12} t\right)=2\nonumber\] Dividiendo por$4$
\[\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\nonumber\] Sabemos$\sin \left(\theta \right)=\dfrac{1}{2}$ cuándo$\theta =\dfrac{\pi }{6} \quad or\quad \theta =\dfrac{5\pi }{6}$

Si bien sabemos de qué ángulos tienen un valor sinusoidal$\dfrac{1}{2}$, debido al estiramiento/compresión horizontal queda menos claro cómo proceder.

Para hacer frente a esto, podemos hacer una sustitución, definiendo una nueva variable temporal$u$ a ser$u=\dfrac{\pi }{12} t$, así nuestra ecuación$\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}$ se convierte en

\[\sin \left(u\right)=\dfrac{1}{2}\nonumber\]

Desde antes, vimos que las soluciones a esta ecuación eran

\[u=\dfrac{\pi }{6} +2\pi k\nonumber\]donde$k$ es un número entero, y
\[u=\dfrac{5\pi }{6} +2\pi k\nonumber\] donde k es un número entero

Para deshacer nuestra sustitución, reemplazamos el$u$ en las soluciones con$u=\dfrac{\pi }{12} t$ y resolvemos para$t$.

$\dfrac{\pi }{12} t=\dfrac{\pi }{6} +2\pi k$donde$k$ es un entero, y$\dfrac{\pi }{12} t=\dfrac{5\pi }{6} +2\pi k$ donde$k$ es un entero.

Dividiendo por$\pi $ /12, obtenemos soluciones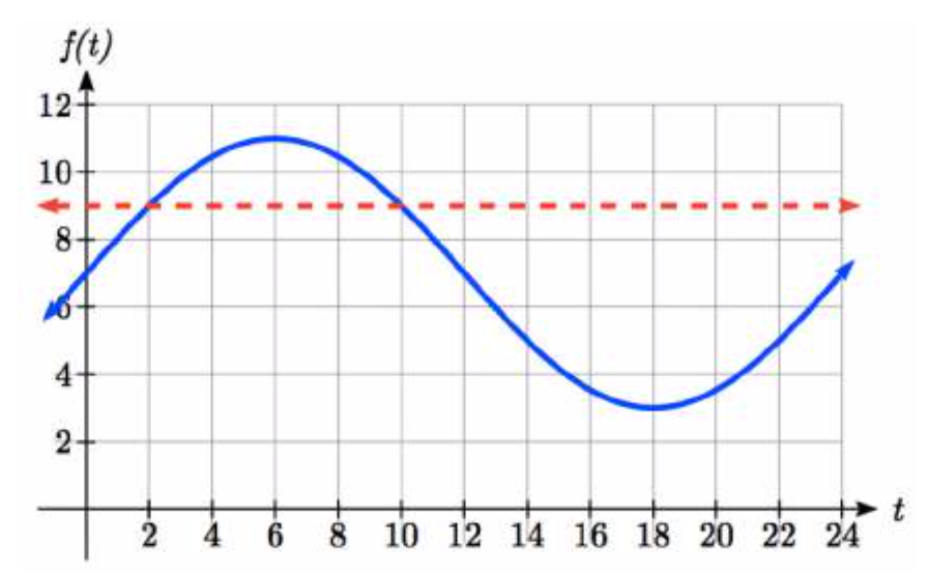 $En una ventana de t es igual a 0 a 24, una gráfica sinusoidal que comienza aumentando en 0 coma 7 hasta 6 coma 11, luego disminuye pasando por 12 coma 7 en el camino hacia abajo a 18 coma 3, antes de volver a aumentar a 24 coma 7. Una línea discontinua horizontal a una salida de 9 interseca la gráfica sinusoidal en dos ubicaciones, alrededor de t es igual a 2 y t es igual a 10.$

$t=2+24k$donde$k$ es un entero, y$t=10+24k$ donde$k$ es un entero.

La profundidad será de 9 pies y la embarcación podrá acercarse al muelle entre las 2 am y las 10 am.

Observe cómo en ambos escenarios, el 24k muestra cómo cada 24 horas se repetirá el ciclo.

En el ejemplo anterior, mirando hacia atrás a la ecuación simplificada original$\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}$, podemos usar la relación del “período normal” al factor de estiramiento para encontrar el período:$\dfrac{2\pi }{\left(\dfrac{\pi }{12} \right)} =2\pi \left(\dfrac{12}{\pi } \right)=24$. Observe que la función sinusoidal tiene un periodo de 24, lo que se refleja en las soluciones: hubo dos soluciones únicas en un ciclo completo de la función sinusoidal, y se encontraron soluciones adicionales al agregar múltiplos de un periodo completo.

Ejercicio$\PageIndex{2}$

Resolver$4\sin (5t)-1=1$ para todos los valores posibles de$t$.

Contestar

\[4\sin (5t)-1=1\nonumber\]

\[\sin (5t)=\dfrac{1}{2}\nonumber\]Que$u=5t$ así se convierta esto$\sin (u)=\dfrac{1}{2}$, que tiene soluciones

\[u=\dfrac{\pi }{6} +2\pi k,\dfrac{5\pi }{6} +2\pi k\nonumber\]Resolver\[5t=u=\dfrac{\pi }{6} +2\pi k,\dfrac{5\pi }{6} +2\pi k\nonumber\] da las soluciones

\[t=\dfrac{\pi }{30} +\dfrac{2\pi }{5} k\qquad t=\dfrac{\pi }{6} +\dfrac{2\pi }{5} k\nonumber\]

Resolver usando las funciones de trigonometría inversa

No todas las ecuaciones involucran los valores “especiales” de las funciones trigonométricas que hemos aprendido. Para encontrar las soluciones a estas ecuaciones, necesitamos usar las funciones trigonométricas inversas.

Ejemplo$\PageIndex{4}$

Utilice la función sinusoidal inversa para encontrar una solución a$\sin \left(\theta \right)=0.8$.

Solución

Dado que no se trata de un valor de círculo unitario conocido, calculando la inversa,$\theta =\sin ^{-1} \left(0.8\right)$. Esto requiere una calculadora y debemos aproximar un valor para este ángulo. Si tu calculadora está en modo grados, tu calculadora te dará un ángulo en grados como salida. Si tu calculadora está en modo radianes, tu calculadora te dará un ángulo en radianes. En radianes,$\theta =\sin ^{-1} \left(0.8\right)\approx 0.927$, o en grados,$\theta =\sin ^{-1} \left(0.8\right)\approx 53.130{}^\circ$.

Si estás trabajando con una función trig compuesta y no estás resolviendo un ángulo, querrás asegurarte de que estás trabajando en radianes. En el cálculo, casi siempre vamos a querer trabajar con radianes ya que son sin unidades.

Observe que las funciones trig inversas hacen exactamente lo que esperaría de cualquier función; por cada entrada dan exactamente una salida. Si bien esto es necesario para que estos sean una función, significa que para encontrar todas las soluciones a una ecuación como$\sin \left(\theta \right)=0.8$, necesitamos hacer algo más que evaluar la función inversa.

Para encontrar soluciones adicionales, es bueno recordar cuatro cosas:

El seno es el$y$ valor -valor de un punto en el círculo unitario
El coseno es el$x$ -valor de un punto en el círculo unitario
La tangente es la pendiente de una línea en un ángulo dado
Otros ángulos con el mismo$\sin$/$\cos$/$\tan$tendrán el mismo ángulo de referencia

Ejemplo$\PageIndex{5}$

Encuentre todas las soluciones para$\sin \left(\theta \right)=0.8$.

Solución

Esperaríamos que dos ángulos únicos en un ciclo tengan este valor sinusoidal. En el ejemplo anterior, encontramos una solución para ser$\theta =\sin ^{-1} \left(0.8\right)\approx 0.927$. Para encontrar al otro, necesitamos responder a la pregunta “¿qué otro ángulo tiene el mismo valor sinusoidal que un ángulo de 0.927?” 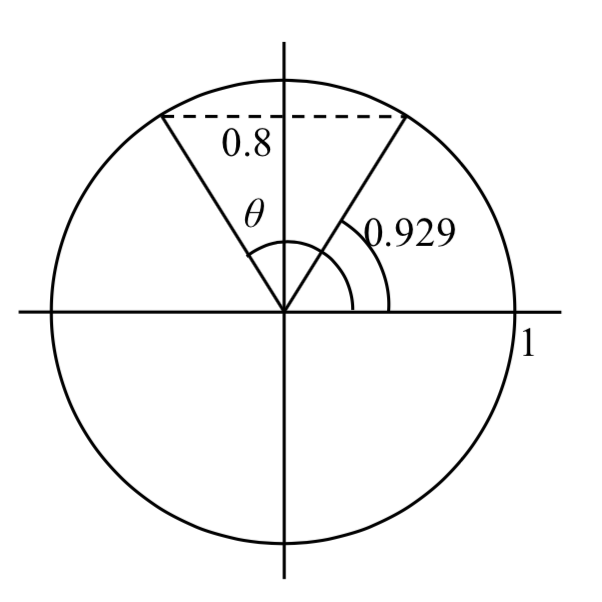$Un círculo unitario centrado en el origen. Se muestra una línea en el ángulo 0.929, que se encuentra con el círculo en un punto con valor y 0.8. Se muestra una segunda línea en el segundo cuadrante con ángulo theta que también se encuentra con el círculo a un valor y de 0.8.$

Podemos pensar en esto como encontrar todos los ángulos donde el valor y en el círculo unitario es 0.8. Dibujar una imagen del círculo ayuda a cómo la simetría.

En un círculo unitario, reconoceríamos que el segundo ángulo tendría el mismo ángulo de referencia y residiría en el segundo cuadrante. Este segundo ángulo estaría ubicado en$\theta =\pi -\sin ^{-1} (0.8)$, o aproximadamente$\theta \approx \pi -0.927=2.214$.

Para encontrar más soluciones recordamos que los ángulos coterminales con estos dos tendrían el mismo valor sinusoidal, por lo que podemos sumar ciclos completos de 2$\pi $.

\[\theta =\sin ^{-1} (0.8) +2\pi k\nonumber\]y\[\theta =\pi -\sin ^{-1} (0.8)+2\pi k\nonumber\] donde$k$ es un entero,
o aproximadamente,$\theta =0.927+2\pi k$ y$\theta =2.214+2\pi k$ donde$k$ es un entero.

Ejemplo$\PageIndex{6}$

Encuentra todas las soluciones para$\sin \left(x\right)=-\dfrac{8}{9}$ en el intervalo$0{}^\circ \le x<360{}^\circ$.

Solución

Estamos buscando los ángulos con un$y$ -valor de -8/9 en el círculo unitario. De inmediato podemos ver que las soluciones estarán en el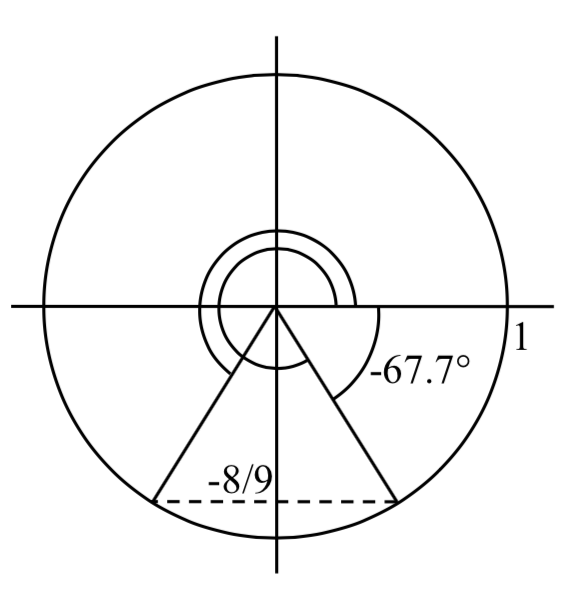 $Un círculo unitario centrado en el origen. Se muestra una línea en ángulo negativo 62.7 grados, que se encuentra con el círculo en un punto con valor y negativo ocho noventes. Otro arco a la misma línea se dibuja en sentido antihorario desde el eje x positivo. Se muestra una segunda línea en el tercer cuadrante que también se encuentra con el círculo en un punto con un valor y de ocho noventa negativos.$ tercer y cuarto cuadrantes.

Primero, giraremos nuestra calculadora al modo grado. Usando la inversa, podemos encontrar una solución$x=\sin ^{-1} \left(-\dfrac{8}{9} \right)\approx -62.734{}^\circ$. Si bien este ángulo satisface la ecuación, no se encuentra en el dominio que estamos buscando. Para encontrar los ángulos en el dominio deseado, comenzamos a buscar soluciones adicionales.

Primero, un ángulo coterminal con$-62.734{}^\circ$ tendrá el mismo seno. Al agregar una rotación completa, podemos encontrar un ángulo en el dominio deseado con el mismo seno.

\[x=-62.734{}^\circ +360{}^\circ =297.266{}^\circ\nonumber\]

Hay un segundo ángulo en el dominio deseado que se encuentra en el tercer cuadrante. Observe que$62.734{}^\circ$ es el ángulo de referencia para todas las soluciones, por lo que esta segunda solución sería$62.734{}^\circ$ pasada$180{}^\circ$

\[x=62.734{}^\circ +180{}^\circ =242.734{}^\circ\nonumber\]

Las dos soluciones$0{}^\circ \le x<360{}^\circ$ son$x$ =$297.266{}^\circ$ y$x$ =$242.734{}^\circ$

Ejemplo$\PageIndex{7}$

Encuentre todas las soluciones a$\tan \left(x\right)=3$ on$0 \le x<2\pi$.

Solución

Usando la función tangente inversa, podemos encontrar una solución$x=\tan ^{-1} \left(3\right) \approx 1.249$. A diferencia del seno y el coseno, la función tangente solo alcanza cualquier valor de salida una vez por ciclo, por lo que no hay una segunda solución en ningún ciclo. 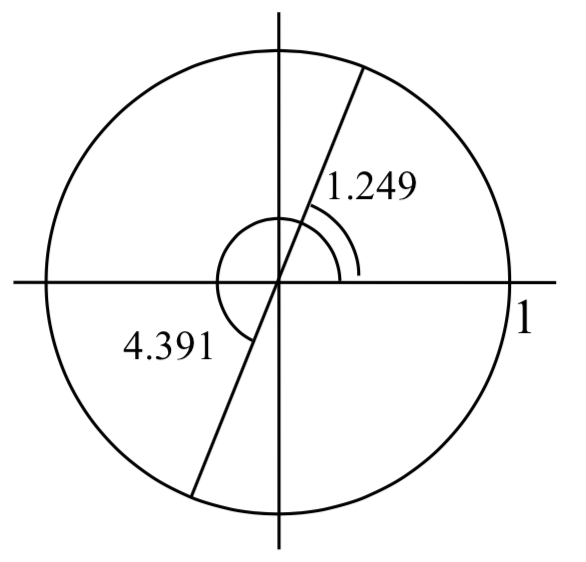$Un círculo unitario centrado en el origen. Se muestra una línea en ángulo 1.249. Se muestra una segunda línea en ángulo 4.391, la cual tiene la misma pendiente que la primera línea.$

Al sumar$\pi $, un periodo completo de función tangente, podemos encontrar un segundo ángulo con el mismo valor tangente. Observe que esto da otro ángulo donde la línea tiene la misma pendiente.

Si se desearan soluciones adicionales, podríamos seguir agregando múltiplos de$\pi $, por lo que todas las soluciones tomarían la forma$x=1.249+k\pi$, sin embargo solo nos interesa$0 \le x< 2\pi$.

\[x=1.249+\pi =4.391\nonumber\]

Las dos soluciones en$0\le x<2\pi$ son$x = 1.249$ y$x = 4.391$.

Ejercicio$\PageIndex{3}$

Encuentre todas las soluciones a$\tan \left(x\right)=0.7$ on$0{}^\circ \le x<360{}^\circ$.

Contestar

La primera solución es$x=\tan ^{-1} (0.7) \approx 34.992{}^\circ$.

Para una tangente estándar, la segunda solución se puede encontrar agregando un período completo,$180\mathrm{{}^\circ}$, dando\[x=180{}^\circ +34.99{}^\circ =214.992{}^\circ\nonumber\]

Ejemplo$\PageIndex{8}$

Resuelva$3\cos \left(t\right)+4=2$ para todas las soluciones en un ciclo,$0\le t<2\pi$

Solución

\[3\cos \left(t\right)+4=2\nonumber\]Aislar el coseno
\[3\cos \left(t\right)=-2\nonumber\]
\[\cos \left(t\right)=-\dfrac{2}{3}\nonumber\] Usando la inversa, podemos encontrar una solución
\[t=\cos ^{-1} \left(-\dfrac{2}{3} \right)\approx 2.301\nonumber\]

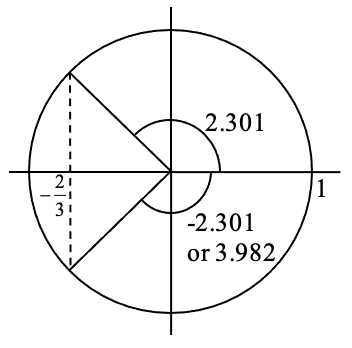
$Un círculo unitario centrado en el origen. En el segundo cuadrante se muestra una línea en el ángulo 2.301 que se encuentra con el círculo en un punto con valor x negativo de dos tercios. Hay una segunda línea en el tercer cuadrante que también se encuentra con el círculo en un punto con valor x negativo dos tercios. Está etiquetado como que tiene ángulo negativo 2.301 o 3.982$

Buscamos dos ángulos donde la$x$ coordenada -en un círculo unitario sea -2/3. Un segundo ángulo con el mismo coseno se ubicaría en el tercer cuadrante. Observe que la ubicación de este ángulo podría representarse como$t=-2.301$. Para representar esto como un ángulo positivo podríamos encontrar un ángulo coterminal agregando un ciclo completo.

\[t=-2.301+2\pi = 3.982\nonumber\]

La ecuación tiene dos soluciones entre 0 y 2$\pi $, at$t = 2.301$ y$t = 3.982$.

Ejemplo$\PageIndex{9}$

Resuelva$\cos \left(3t\right)=0.2$ para todas las soluciones en dos ciclos,$0\le t<\dfrac{4\pi }{3}$.

Solución

Como antes, con una compresión horizontal puede ser útil hacer una sustitución,$u=3t$ Hacer esta sustitución simplifica la ecuación a una forma que ya hemos resuelto.

\[\cos \left(u\right)=0.2\nonumber\]
\[u=\cos ^{-1} \left(0.2\right)\approx 1.369\nonumber\]

Una segunda solución en un ciclo se ubicaría en el cuarto cuadrante con el mismo ángulo de referencia.

\[u=2\pi -1.369=4.914\nonumber\]

En este caso, necesitamos todas las soluciones en dos ciclos, por lo que necesitamos encontrar las soluciones en el segundo ciclo. Podemos hacer esto agregando una rotación completa a las dos soluciones anteriores.

\[\begin{array}{l} {u=1.369+2\pi =7.653} \\ {u=4.914+2\pi =11.197} \end{array}\nonumber\]

Deshaciendo la sustitución, obtenemos nuestras cuatro soluciones:

\[3t = 1.369\text{, so }t = 0.456\nonumber\]
\[3t = 4.914\text{, so }t = 1.638\nonumber\]
\[3t = 7.653\text{, so }t = 2.551\nonumber\]
\[3t = 11.197\text{, so }t = 3.732\nonumber\]

Ejemplo$\PageIndex{10}$

Resuelve$3\sin \left(\pi \, t\right)=-2$ para todas las soluciones.

Solución

\[3\sin \left(\pi \, t\right)=-2\nonumber\]Aislar el seno

\[\sin \left(\pi \, t\right)=-\dfrac{2}{3}\nonumber\]Hacemos la sustitución$u=\pi \, t$

\[\sin \left(u\right)=-\dfrac{2}{3}\nonumber\]Usando la inversa, encontramos una solución

\[u=\sin ^{-1} \left(-\dfrac{2}{3} \right)\approx -0.730\nonumber\]

Este ángulo está en el cuarto cuadrante. Un segundo ángulo con el mismo seno estaría en el tercer cuadrante con 0.730 como ángulo de referencia:

\[u=\pi +0.730=3.871\nonumber\]

Podemos escribir todas las soluciones a la ecuación$\sin \left(u\right)=-\dfrac{2}{3}$ como

\[u=-0.730+2\pi {\kern 1pt} k\text{ or }u=3.871+2\pi {\kern 1pt} k\nonumber\]donde$k$ es un número entero.

Deshaciendo nuestra sustitución, podemos reemplazar u en nuestras soluciones con$u=\pi \, t$ y resolver para$t$

\[\pi t=-0.730+2\pi k\text{ or }\pi t=3.871+2\pi k\nonumber\]

Dividir por$\pi $
\[ t=-0.232+2 k\text{ or } t=1.232+2 k\nonumber\]

Ejercicio$\PageIndex{4}$

Resuelva$5\sin \left(\dfrac{\pi }{2} t\right)+3=0$ para todas las soluciones en un ciclo,$0 \le t < 4$.

Contestar

\[\sin \left(\dfrac{\pi }{2} t\right)=-\dfrac{3}{5}\nonumber\]Vamos$u=\dfrac{\pi }{2} t$, así que esto se convierte\[\sin \left(u\right)=-\dfrac{3}{5}\nonumber\]

Usando el inverso,$u=\sin ^{-1} \left(-\dfrac{3}{5} \right)\approx -0.6435$. Como queremos soluciones positivas, podemos encontrar la solución coterminal agregando un ciclo completo:$u=-0.6435+2\pi =5.6397$. Otro ángulo con el mismo pecado estaría en el tercer cuadrante con el ángulo de referencia 0.6435. $u=\pi +0.6435=3.7851$.

Resolviendo para$t$\[u=\dfrac{\pi }{2} t=5.6397\nonumber\], así\[t=5.6397\left(\dfrac{2}{\pi } \right)=3.5903\nonumber\]
y\[u=\dfrac{\pi }{2} t=3.7851\nonumber\], así\[t=3.7851\left(\dfrac{2}{\pi } \right)=2.4097\nonumber\]
\[t = 2.4097\text{ or }t = 3.5903\nonumber\]

RESOLVER ECUACIONES TRIGONOMETRÍA: FUNCIONES SINUSO

Aislar la función trigonométrica en un lado de la ecuación
Hacer una sustitución para el interior del seno, coseno o tangente (u otra función trigonométrica)
Utilice funciones trigonométricas inversas para encontrar una solución
Usar simetrías para encontrar una segunda solución en un ciclo (cuando existe una segunda)
Encuentre soluciones adicionales si es necesario agregando períodos completos
Deshacer la sustitución

Ahora podemos volver a la pregunta con la que iniciamos la sección.

Ejemplo$\PageIndex{11}$

La altura de un piloto en la noria London Eye puede ser determinada por la ecuación$h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70$. ¿Cuánto tiempo tiene el jinete a más de 100 metros sobre el suelo?

Solución

Para saber cuánto tiempo está el jinete por encima de los 100 metros, primero encontramos los tiempos en los que el jinete se encuentra a una altura de 100 metros resolviendo h (t) = 100.

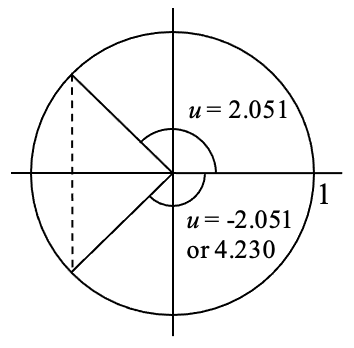
$Un círculo unitario centrado en el origen. En el segundo cuadrante se muestra una línea en el ángulo u igual a 2.051. Hay una segunda línea en el tercer cuadrante que se encuentra con el círculo en un punto con el mismo valor x que el punto donde la primera línea se encuentra con el círculo. La segunda línea está etiquetada como que tiene un ángulo u es igual a negativo 2.051 o 4.230$

\[100=-65\cos \left(\dfrac{\pi }{15} t\right)+70\nonumber\]Aislar el coseno
\[30=-65\cos \left(\dfrac{\pi }{15} t\right)\nonumber\]
\[\dfrac{30}{-65} =\cos \left(\dfrac{\pi }{15} t\right)\nonumber\] Hacemos la sustitución$u=\dfrac{\pi }{15} t$
\[\dfrac{30}{-65} =\cos (u)\nonumber\] Usando la inversa, encontramos una solución
\[u=\cos ^{-1} \left(\dfrac{30}{-65} \right)\approx 2.051\nonumber\]

Este ángulo está en el segundo cuadrante. Un segundo ángulo con el mismo coseno sería simétrico en el tercer cuadrante. Este ángulo podría representarse como u = -2.051, pero necesitamos un ángulo positivo coterminal, por lo que sumamos 2$\pi $:

\[u=2\pi -2.051\approx 4.230\nonumber\]

Ahora podemos deshacer la sustitución para resolver$t$

$\dfrac{\pi }{15} t=2.051$así que$t = 9.793$ minutos después del inicio del viaje
$\dfrac{\pi }{15} t=4.230$ así que$t = 20.197$ minutos después del inicio del viaje

Un piloto estará a 100 metros después de 9.793 minutos, y nuevamente después de 20.197 minutos. Por el comportamiento de la gráfica de altura, sabemos que el piloto estará por encima de los 100 metros entre estos tiempos. Un piloto estará por encima de los 100 metros para 20.197 - 9.793 = 10.404 minutos del recorrido.

Temas Importantes de esta Sección

Resolver ecuaciones trigonométricas usando valores conocidos
Uso de la sustitución para resolver ecuaciones
Encontrar respuestas en un ciclo o periodo vs. encontrar todas las soluciones posibles
Método para resolver ecuaciones trig