8.1: Triángulos no rectos - Leyes de los senos y cosenos

Última actualización
Guardar como PDF

Page ID: 116885

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Si bien los triángulos rectos nos permiten resolver muchas aplicaciones, es más común encontrar escenarios donde el triángulo que nos interesa no tenga un ángulo recto.

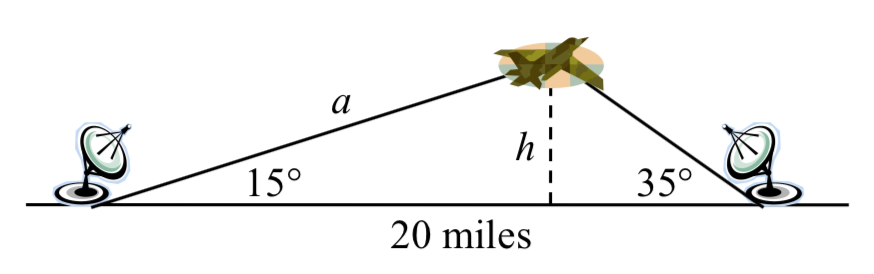
Dos estaciones de radar ubicadas a 20 millas de distancia detectan un OVNI ubicado entre ellas. El ángulo de elevación medido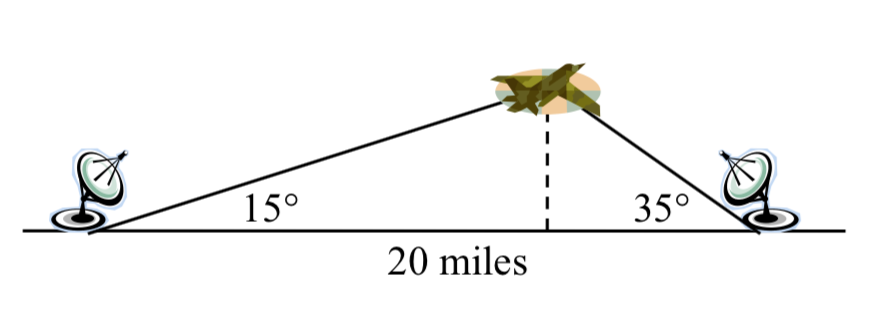 $Dos estaciones de radar se muestran en un eje horizontal, separadas por 20 millas. Se muestra un avión entre las estaciones y por encima del eje horizontal. Se dibuja una línea discontinua desde el avión hasta el eje horizontal. Una línea desde la estación izquierda hasta el avión tiene un ángulo de 15 grados con respecto al eje horizontal. Una línea desde la estación derecha hasta el avión tiene un ángulo de 35 grados con respecto al eje horizontal.$ por la primera estación es de 35 grados. El ángulo de elevación medido por la segunda estación es de 15 grados. ¿Cuál es la altitud del OVNI?

Vemos que el triángulo formado por el OVNI y las dos estaciones no es un triángulo rectángulo. Por supuesto, en cualquier triángulo podríamos dibujar una altitud, una línea perpendicular desde un vértice al lado opuesto, formando dos triángulos rectos, pero sería bueno tener métodos para trabajar directamente con triángulos no rectos. En esta sección, ampliaremos la trigonometría del triángulo rectángulo que aprendimos en el Capítulo 5, y la adaptaremos a triángulos no rectos.

Ley de los Sines

Dado un triángulo arbitrario no rectángulo, podemos bajar una altitud, que etiquetamos temporalmente$h$, para crear dos triángulos rectos.

Usando las relaciones del triángulo rectángulo,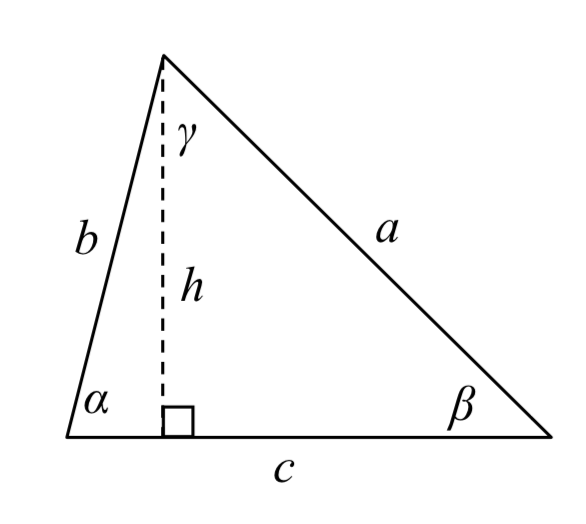 $Se muestra un triángulo no recto. Un ángulo alfa es lado opuesto etiquetado a. Un ángulo beta es lado opuesto etiquetado b. Un ángulo gamma es lado opuesto etiquetado c. Una línea discontinua etiquetada h se dibuja desde la esquina con ángulo gamma al lado c, formando un ángulo recto con lado c.$

\[\sin (\alpha ) = \dfrac{h}{b}\text{ and }\sin (\beta ) = \dfrac{h}{a}\nonumber\]

Resolviendo ambas ecuaciones para$h$, obtenemos$b\sin (\alpha ) = h$ y$a\sin (\beta ) = h$. Ya que el$h$ es lo mismo en ambas ecuaciones, establecemos$b\sin (\alpha ) = a\sin (\beta )$. Dividiendo ambos lados por$ab$, concluimos que

\[\dfrac{\sin (\alpha )}{a} = \dfrac{\sin (\beta )}{b}\nonumber\]

Si hubiéramos dibujado la altitud para que fuera perpendicular a lado$b$ o$a$, podríamos establecer de manera similar

\[\dfrac{\sin (\alpha )}{a} = \dfrac{\sin (\gamma )}{c}\text{ and }\dfrac{\sin (\beta )}{b} = \dfrac{\sin (\gamma )}{c}\nonumber\]

Colectivamente, estas relaciones se llaman la Ley de los Sines.

LEY DE SINES

Dado un triángulo con ángulos y lados opuestos etiquetados como se muestra, la relación de seno de ángulo a longitud del lado opuesto siempre será igual, o, simbólicamente,

\[\dfrac{\sin (\alpha )}{a} = \dfrac{\sin (\beta )}{b} = \dfrac{\sin (\gamma )}{c}\]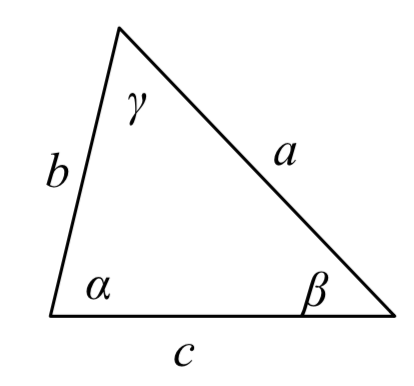 $Se muestra un triángulo no recto. Un ángulo alfa es lado opuesto etiquetado a. Un ángulo beta es lado opuesto etiquetado b. Un ángulo gamma es lado opuesto etiquetado c.$

Para mayor claridad, llamamos lado$a$ al lado correspondiente del ángulo$\alpha$.

De igual manera, llamamos ángulo$\alpha$, el ángulo de lado correspondiente$a$.

De igual manera para lado$b$ y ángulo$\beta$, y para lado$c$ y ángulo$\gamma$.

Cuando usamos la ley de los senos, usamos cualquier par de proporciones como ecuación. En el caso más sencillo, conocemos dos ángulos y uno de los lados correspondientes.

Ejemplo$\PageIndex{1}$

En el triángulo que se muestra aquí, resuelva para los lados y ángulo desconocidos.

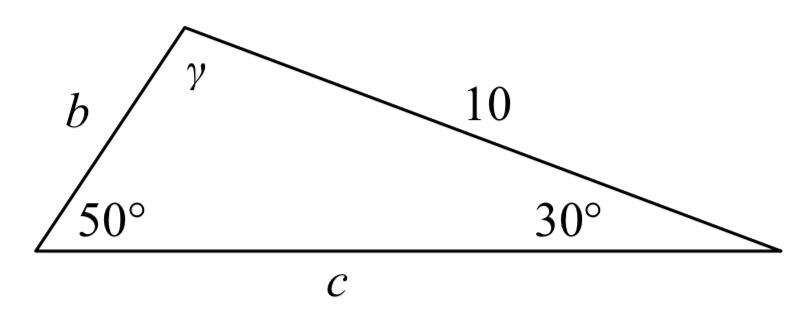
$Se muestra un triángulo no recto. Un ángulo de 30 grados es lado opuesto etiquetado b. Un ángulo de 50 grados es lado opuesto etiquetado 10. Un ángulo obtuso gamma es lado opuesto etiquetado c.$

Solución

Resolver para el ángulo desconocido es relativamente fácil, ya que los tres ángulos deben sumar 180 grados.

A partir de esto, podemos determinar que

\[\gamma = 180^{\circ} - 50^{\circ} - 30^{\circ} = 100^{\circ}\nonumber\]

Para encontrar un lado desconocido, necesitamos conocer el ángulo correspondiente, y también necesitamos otra relación conocida.

Ya que conocemos el ángulo$50^{\circ}$ y su lado correspondiente, podemos usar esto para una de las dos relaciones. Para buscar lado$b$, usaríamos su ángulo correspondiente,$30^{\circ}$.

\[\dfrac{\sin (50^\circ )}{10} = \dfrac{\sin (30^\circ )}{b}\nonumber\]Multiplicar ambos lados por$b$
\[b\dfrac{\sin (50^\circ )}{10} = \sin (30^\circ )\nonumber\] Dividir, o multiplicar por el recíproco, para resolver por$b$
\[b = \sin (30^\circ )\dfrac{10}{\sin (50^\circ )} \approx 6.527\nonumber\]

Del mismo modo, para resolver por lado$c$, configuramos la ecuación

\[\dfrac{\sin (50^\circ )}{10} = \dfrac{\sin (100^\circ )}{c}\nonumber\]
\[c = \sin (100^\circ )\dfrac{10}{\sin (50^\circ )} \approx 12.856\nonumber\]

Ejemplo$\PageIndex{2}$

Encuentra la elevación del OVNI desde el inicio de la sección.

$Dos estaciones de radar se muestran en un eje horizontal, separadas por 20 millas. Se muestra un avión entre las estaciones y por encima del eje horizontal. Una línea discontinua etiquetada con h se dibuja desde el avión hasta el eje horizontal. Una línea etiquetada como desde la estación izquierda hasta el avión tiene un ángulo de 15 grados con respecto al eje horizontal. Una línea desde la estación derecha hasta el avión tiene un ángulo de 35 grados con respecto al eje horizontal.$

Solución

Para encontrar la elevación del OVNI, primero encontramos la distancia de una estación al OVNI, como el lado a en la imagen, luego usamos relaciones de triángulo rectángulo para encontrar la altura del OVNI,$h$.

Dado que los ángulos en el triángulo se suman a 180 grados, el ángulo desconocido del triángulo debe ser$180^{\circ} - 15^{\circ} - 35^{\circ} = 130^{\circ}$. Este ángulo es opuesto al lado de la longitud 20, lo que nos permite establecer una relación de Ley de Sines:

\[\dfrac{\sin (130^\circ )}{20} = \dfrac{\sin (35^\circ )}{a}\nonumber\]Multiplicar por$a$
\[a\dfrac{\sin (130^\circ )}{20} = \sin (35^\circ )\nonumber\] Dividir, o multiplicar por el recíproco, para resolver para$a$
\[a = \dfrac{20\sin (35^\circ )}{\sin (130^\circ )} \approx 14.975\nonumber\] Simplificar

La distancia de una estación al OVNI es de aproximadamente 15 millas. Ahora que conocemos una, podemos usar relaciones de triángulo rectángulo para resolver$h$.

\[\sin (15^\circ ) = \dfrac{opposite}{hypotenuse} = \dfrac{h}{a} = \dfrac{h}14.975\nonumber\]Resolver para$h$
\[h = 14.975\sin (15^\circ ) \approx 3.876\nonumber\]

El OVNI se encuentra a una altitud de 3.876 millas.

Además de resolver triángulos en los que se conocen dos ángulos, la ley de los senos se puede utilizar para resolver para un ángulo cuando se conocen dos lados y un ángulo correspondiente.

Ejemplo$\PageIndex{3}$

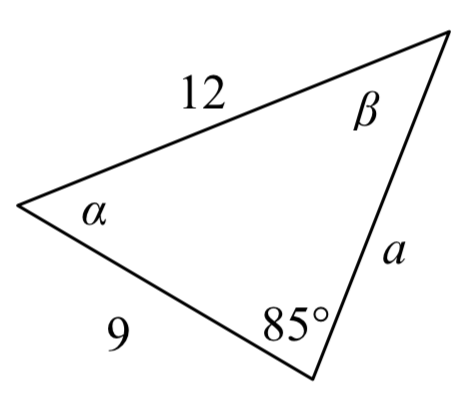
En el triángulo que se muestra aquí, resuelva para los lados y ángulos desconocidos.

$Se muestra un triángulo no recto. Un ángulo de 85 grados es opuesto a una longitud lateral 12. Un ángulo beta es opuesto a una longitud lateral 9. Un ángulo alfa es opuesto a una longitud lateral a.$

Solución

Al elegir qué par de proporciones de la Ley de Sines usar, siempre queremos elegir un par donde conozcamos tres de las cuatro piezas de información en la ecuación. En este caso, conocemos el ángulo$85^{\circ}$ y su lado correspondiente, por lo que usaremos esa relación. Dado que nuestra única otra información conocida es el lado con longitud 9, usaremos ese lado y resolveremos su ángulo correspondiente.

\[\dfrac{\sin (85^\circ )}{12} = \dfrac{\sin (\beta )}{9}\nonumber\]Aislar lo desconocido
\[\dfrac{9\sin (85^\circ )}{12} = \sin (\beta )\nonumber\] Usa el seno inverso para encontrar una primera solución

Recuerda cuando usamos la función inversa que hay dos respuestas posibles.

\[\beta = {\sin ^{ - 1}}\left( \dfrac{9\sin (85^\circ )}{12} \right) \approx 48.3438^\circ \nonumber\]Por simetría encontramos la segunda solución posible
\[\beta = 180^\circ - 48.3438^\circ = 131.6562^\circ \nonumber\]

En este segundo caso, si$\beta \approx 132^{\circ}$, entonces$\alpha$ sería$\alpha = 180^{\circ} - 85^{\circ} - 132^{\circ} = -37^{\circ}$, lo cual no tiene sentido, entonces la única posibilidad para este triángulo es$\beta = 48.3438^{\circ}$.

Con un segundo ángulo, ahora podemos encontrar fácilmente el tercer ángulo, ya que los ángulos deben sumar a$180^{\circ}$, así$\alpha = 180^{\circ} – 85^{\circ} – 48.3438^{\circ} = 46.6562^{\circ}$.

Ahora que sabemos$\alpha$, podemos proceder como en ejemplos anteriores para encontrar el lado desconocido$a$.

\[\dfrac{\sin (85^\circ )}{12} = \dfrac{\sin (46.6562^\circ )}{a}\nonumber\]
\[a = \dfrac{12\sin (46.6562^\circ )}{\sin (85^\circ )} \approx 8.7603\nonumber\]

Observe que en el problema anterior, cuando utilizamos Ley de Sinos para resolver por un ángulo desconocido, puede haber dos posibles soluciones. Esto se llama el caso ambiguo, y puede surgir cuando conocemos dos lados y un ángulo no incluido. En el caso ambiguo podemos encontrar que un conjunto particular de información dada puede conducir a 2, 1 o ninguna solución en absoluto. Sin embargo, cuando se dispone de una imagen precisa del triángulo o contexto adecuado, podemos determinar qué ángulo se desea.

Ejercicio$\PageIndex{1}$

Dado$\alpha = 80^\circ ,a = 120,{\rm{ and }}b = 121$, encuentra el lado y los ángulos correspondientes y faltantes. Si hay más de una solución posible, mostrar ambas.

Contestar

\[\frac{\sin (80^{\circ })}{120}=\frac{\sin (\beta )}{121}\nonumber\]

\[1^{\text{st}}\text{ possible solution }\begin{array}{l}\beta = 83.2^\circ \\\gamma = 16.8^\circ \\c = 35.2\end{array}\nonumber\]

\[2^{\text{nd}}\text{ solution }\begin{array}{l}\beta = 96.8^\circ \\\gamma = 3.2^\circ \\c = 6.9\end{array}\nonumber\]

Si nos dieran una imagen del triángulo podría ser posible eliminar uno de estos

Ejemplo$\PageIndex{4}$

Encuentra todos los triángulos posibles si un lado tiene longitud 4 opuesto a un ángulo de$50^{\circ}$ y un segundo lado tiene longitud 10.

Solución

Usando la información dada, podemos buscar el ángulo opuesto al lado de la longitud 10.

\[\dfrac{\sin (50^\circ )}{4} = \dfrac{\sin (\alpha )}{10}\nonumber\]
\[\sin (\alpha ) = \dfrac{10\sin (50^\circ )}{4} \approx 1.915\nonumber\]

Dado que el rango de la función sinusoidal es [-1, 1], es imposible que el valor sinusoidal sea 1.915. No hay triángulos que se puedan dibujar con las dimensiones proporcionadas.

Ejemplo$\PageIndex{5}$

Encuentra todos los triángulos posibles si un lado tiene longitud 6 opuesto a un ángulo de$50^{circ}$ y un segundo lado tiene longitud 4.

Solución

Usando la información dada, podemos buscar el ángulo opuesto al lado de la longitud 4.

\[\dfrac{\sin (50^\circ )}{6} = \dfrac{\sin (\alpha )}{4}\nonumber\]
\[\sin (\alpha ) = \dfrac{4\sin (50^\circ )}{6} \approx 0.511\nonumber\]Usa la inversa para encontrar una solución
\[\alpha = {\sin ^{ - 1}}\left( {0.511} \right) \approx 30.710^\circ \nonumber\] Por simetría hay una segunda solución posible
\[\alpha = 180^\circ - 30.710^\circ = 149.290^\circ \nonumber\]

Si usamos el ángulo$30.710^\circ $, el tercer ángulo sería$180^\circ - 50^\circ - 30.710^\circ = 99.290^\circ $. Entonces podremos volver a usar Ley de Sines para encontrar el tercer lado.

\[\dfrac{\sin (50^\circ )}{6} = \dfrac{\sin (99.290^\circ )}{c}\nonumber\]Resolver para$c$
\[c = 7.730\nonumber\]

Si usáramos el ángulo$\alpha = 149.290^{\circ}$, el tercer ángulo sería$180^{\circ} – 50^{\circ} – 149.290^{\circ} = –19.29^{\circ}$, lo cual es imposible, por lo que el triángulo anterior es el único posible.

Ejercicio$\PageIndex{2}$

Dado$\alpha = 80^\circ ,a = 100,{\rm{ and }}b = 10$ encontrar el lado y los ángulos faltantes. Si hay más de una solución posible, mostrar ambas.

Contestar: \[\dfrac{\sin \left( {80^\circ } \right)}{120} = \dfrac{\sin \left( \beta \right)}{10}\quad \beta = 5.65^\circ \text{ or }\beta = 174.35^\circ \nonumber\]; sólo el primero es razonable.
\[\gamma = 180^\circ - 5.65^\circ - 80^\circ = 94.35^\circ \nonumber\]
\[\frac{\sin (80^{\circ })}{120}=\frac{\sin (94.35 ^{\circ })}{c}\nonumber\]
\[\beta = 5.65^\circ ,\gamma = 94.35^\circ ,c = 101.25\nonumber\]

Ley de Cosinos

Supongamos que una embarcación sale de puerto, recorre 10 millas, gira 20 grados y recorre otras 8 millas. ¿A qué distancia del puerto está el barco? 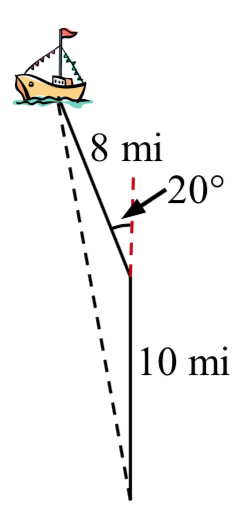$Se muestra una longitud de línea vertical 10 millas. Desde la parte superior, se dibuja una segunda línea de 8 millas de longitud 20 grados en sentido contrario a las agujas del reloj desde la vertical. desde el final se dibuja una línea discontinua hacia la parte inferior de la primera línea.$

Desafortunadamente, si bien la Ley de Sines nos permite abordar muchos casos no triangulares rectos, no nos permite abordar triángulos donde el único ángulo conocido se incluye entre dos lados conocidos, lo que significa que no es un ángulo correspondiente para un lado conocido. Para ello, necesitamos otra herramienta.

Dado un triángulo arbitrario no rectángulo, podemos bajar una altitud, que etiquetamos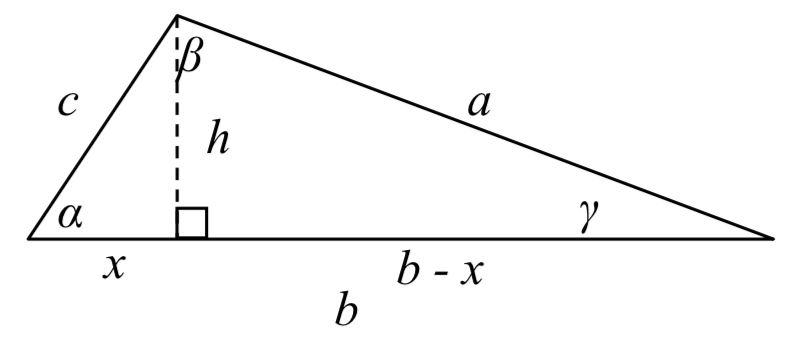 $Se muestra un triángulo no recto, con ángulo alfa opuesto al lado a, ángulo beta opuesto al lado b y ángulo gamma opuesto al lado c. Una línea discontinua etiquetada con h se dibuja desde la esquina con ángulo beta hacia abajo hasta el lado b que se encuentra en ángulo recto. El segmento del lado b a la izquierda de la intersección está etiquetado como x, y el segmento a la derecha está etiquetado como b menos x.$ mporariamente$h$, para crear dos triángulos rectos. Dividiremos la base$b$ en dos piezas, una de las cuales etiquetaremos temporalmente$x$.

A partir de esta imagen, podemos establecer la relación del triángulo rectángulo

\[\cos (\alpha ) = \dfrac{x}{c}\text{ or equivalently,} x = c\cos \left( \alpha \right)\nonumber\]

Usando el Teorema de Pitágoras, podemos establecer

\[{\left( {b - x} \right)^2} + {h^2} = {a^2}\text{ and }{x^2} + {h^2} = {c^2}\nonumber\]

Ambas ecuaciones se pueden resolver para${h^2}$

\[{h^2} = {a^2} - {\left( {b - x} \right)^2}\text{ and }{h^2} = {c^2} - {x^2}\nonumber\]

Dado que el lado izquierdo de cada ecuación es${h^2}$, los lados derechos deben ser iguales

\[{c^2} - {x^2} = {a^2} - {\left( {b - x} \right)^2}\nonumber\]Multiplique el correcto
\[{c^2} - {x^2} = {a^2} - \left( {b^2} - 2bx + {x^2} \right)\nonumber\] Simplificar
\[{c^2} - {x^2} = {a^2} - {b^2} + 2bx - {x^2}\nonumber\]
\[{c^2} = {a^2} - {b^2} + 2bx\nonumber\] Aislar${a^2}$
\[{a^2} = {c^2} + {b^2} - 2bx\nonumber\] Sustituto$c\cos (\alpha ) = x$ desde arriba
\[{a^2} = {c^2} + {b^2} - 2bc\cos (\alpha )\nonumber\]

A este resultado se le llama la Ley de los Cosinos. Dependiendo de qué lado bajamos la altitud, podríamos haber establecido esta relación usando cualquiera de los ángulos. Lo importante a tener en cuenta es que el lado derecho de la ecuación implica un ángulo y los lados adyacentes a ese ángulo — el lado izquierdo de la ecuación involucra el lado opuesto a ese ángulo.

LEY DE COSINES

Dado un triángulo con ángulos y lados opuestos etiquetados como se muestra,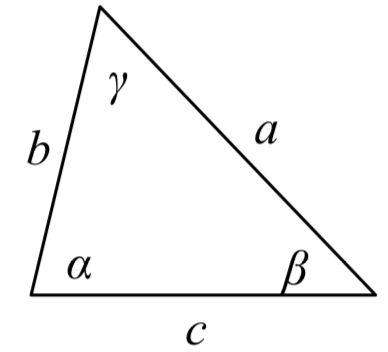 $Se muestra un triángulo no recto. Un ángulo alfa es lado opuesto etiquetado a. Un ángulo beta es lado opuesto etiquetado b. Un ángulo gamma es lado opuesto etiquetado c.$

\[{a^2} = {c^2} + {b^2} - 2bc\cos (\alpha )\]

\[{b^2} = {a^2} + {c^2} - 2ac\cos (\beta )\]

\[{c^2} = {a^2} + {b^2} - 2ab\cos (\gamma )\]

Observe que si uno de los ángulos del triángulo es de 90 grados, cos ($90^{circ}$) = 0, entonces la fórmula

\[{c^2} = {a^2} + {b^2} - 2ab\cos (90^\circ )\nonumber\]Simplifica a
\[{c^2} = {a^2} + {b^2}\nonumber\]

Se debe reconocer esto como el Teorema de Pitágoras. En efecto, a la Ley de Cosinos se le llama a veces el Teorema Generalizado de Pitágoras, ya que extiende el Teorema de Pitágoras a triángulos no rectos.

Ejemplo$\PageIndex{6}$

Volviendo a nuestra pregunta de antes, supongamos que un barco sale de puerto, recorre 10 millas, gira 20 grados y recorre otras 8 millas. ¿A qué distancia del puerto está el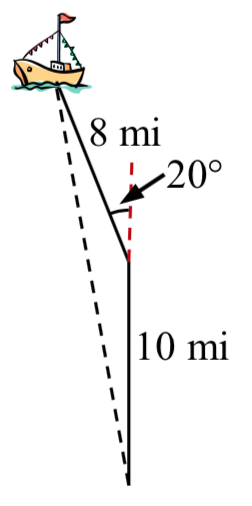 $Se muestra una longitud de línea vertical 10 millas. Desde la parte superior, se dibuja una segunda línea de 8 millas de longitud 20 grados en sentido contrario a las agujas del reloj desde la vertical. desde el final se dibuja una línea discontinua hacia la parte inferior de la primera línea.$ barco?

Solución

El barco giró 20 grados, por lo que el ángulo obtuso del triángulo no recto que se muestra en la imagen es el ángulo suplementario,$180^{\circ} - 20^{\circ} = 160^{\circ}$.

Con esto, podemos utilizar la Ley de Cosinos para encontrar el lado faltante del triángulo obtuso, la distancia desde la embarcación hasta el puerto.

\[{x^2} = {8^2} + {10^2} - 2(8)(10)\cos (160^\circ )\nonumber\]Evaluar el coseno y simplificar la raíz
\[{x^2} = 314.3508\nonumber\] cuadrada en ambos lados
\[x = \sqrt {314.3508} = 17.730\nonumber\]

El barco está a 17.73 millas del puerto.

Ejemplo$\PageIndex{7}$

Encuentra el lado desconocido y los ángulos de este triángulo.

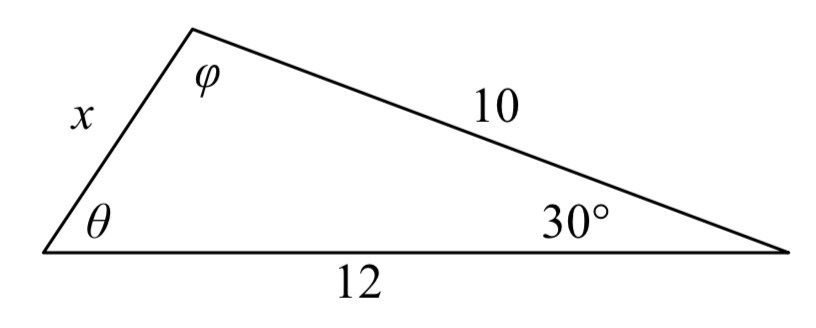
$Se muestra un triángulo no recto. Un ángulo de 30 grados es lado opuesto x. Un ángulo theta es opuesto a la longitud del lado 10. Un ángulo phi es de lado opuesto a la longitud 12.$

Solución

Observe que no tenemos ambas piezas de ningún par lateral/ángulo, por lo que la Ley de Sines no funcionaría con este triángulo.

Ya que tenemos el ángulo incluido entre los dos lados conocidos, podemos recurrir a Ley de Cosinos.

Dado que el lado izquierdo de cualquiera de las ecuaciones de la Ley de Cosinos involucra el lado opuesto al ángulo conocido, el lado izquierdo en esta situación involucrará al lado x Los otros dos lados se pueden usar en cualquier orden.

\[{x^2} = {10^2} + {12^2} - 2(10)(12)\cos (30^\circ )\nonumber\]Evaluar el coseno
\[{x^2} = {10^2} + {12^2} - 2(10)(12)\dfrac{\sqrt 3 }{2}\nonumber\] Simplificar
\[{x^2} = 244 - 120\sqrt 3 \nonumber\] Toma la raíz cuadrada
\[x = \sqrt {244 - 120\sqrt 3 } \approx 6.013\nonumber\]

Ahora que conocemos un ángulo y su lado correspondiente, podemos usar la Ley de los Sinos para rellenar los ángulos restantes del triángulo. Resolviendo para ángulo$\theta$,

\[\dfrac{\sin (30^\circ )}{6.013} = \dfrac{\sin (\theta )}{10}\nonumber\]
\[\sin (\theta ) = \dfrac{10\sin (30^\circ )}{6.013}\nonumber\]Usar el seno inverso
\[\theta = {\sin ^{ - 1}}\left( \dfrac{10\sin (30^\circ )}{6.013} \right) \approx 56.256^\circ \nonumber\]

La otra posibilidad para$\theta$ sería$\theta = 180^{\circ} – 56.256^{\circ} = 123.744^{\circ}$. En la imagen original,$\theta$ hay un ángulo agudo, por lo que 123.744°$^{\circ}$ no tiene sentido si asumimos que la imagen está dibujada a escala.

Continuando con$\theta = 56.256^{\circ}$, entonces podemos encontrar el tercer ángulo del triángulo:

\[\phi = 180^\circ - 30^\circ - 56.256^\circ = 93.744^\circ \nonumber\]

Además de resolver por el lado faltante opuesto a un ángulo conocido, la Ley de Cosinos nos permite encontrar los ángulos de un triángulo cuando conocemos los tres lados.

Ejemplo$\PageIndex{8}$

Resuelve para el ángulo$\alpha$ en el triángulo que se muestra.

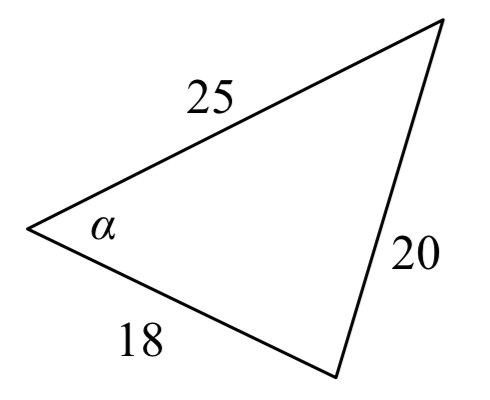
$Un triángulo no rectángulo. El ángulo alfa es la longitud del lado opuesto 20. Los dos lados adyacentes al ángulo alfa tienen longitudes 18 y 25.$

Solución

Utilizando la Ley de los Cosinos,

\[{20^2} = {18^2} + {25^2} - 2(18)(25)\cos (\alpha )\nonumber\]Simplificar
\[400 = 949 - 900\cos (\alpha )\nonumber\]
\[- 549 = - 900\cos (\alpha )\nonumber\]
\[\dfrac{ - 549}{ - 900} = \cos (\alpha )\nonumber\]
\[\alpha = {\cos ^{ - 1}}\left( \dfrac{ - 549}{ - 900} \right) \approx 52.410^\circ \nonumber\]

Ejercicio$\PageIndex{3}$

Dado$\alpha = 25^\circ ,b = 10,{\rm{ and }}c = 20$ encontrar el lado y los ángulos faltantes.

Contestar: \[{a^2} = {10^2} + {20^2} - 2(10)(20)\cos (25^\circ )\quad a = 11.725\nonumber\]
\[\dfrac{\sin \left( {25^\circ } \right)}{11.725} = \dfrac{\sin \left( \beta \right)}{10}\quad \beta = 21.1^\circ \text{ or }\beta = 158.9^\circ \nonumber\]
sólo el primero es razonable ya que 25° + 158.9° superaría 180°.
\[\gamma = 180^\circ - 21.1^\circ - 25^\circ = 133.9^\circ \nonumber\]
\[\beta = 21.1^\circ , \gamma = 133.9^\circ , a = 11.725\nonumber\]

Observe que dado que el coseno inverso puede devolver cualquier ángulo entre 0 y 180 grados, no habrá ningún caso ambiguo al usar Ley de Cosinos para encontrar un ángulo.

Ejemplo$\PageIndex{9}$

En muchos celulares con GPS, se puede dar una ubicación aproximada antes de recibir la señal GPS. Esto se realiza mediante un proceso llamado triangulación, que funciona utilizando la distancia desde dos puntos conocidos. Supongamos que hay dos torres de telefonía celular a tu alcance, ubicadas a 6000 pies de distancia a lo largo de una carretera recta que corre de este a oeste, y sabes que estás al norte de la carretera. Basado en el retardo de la señal, se puede determinar que estás a 5050 pies de la primera torre y 2420 pies de la segunda. Determina tu posición al norte y al este de la primera torre, y determina a qué distancia estás de la autopista.

Solución

Por simplicidad, comenzamos por dibujar un cuadro y etiquetar nuestra información dada. Usando la Ley de Cosinos, podemos resolver f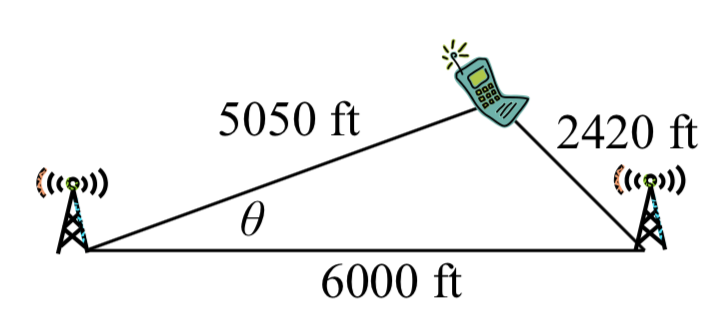 $Dos torres se muestran horizontalmente a 6000 pies de distancia. Un celular se muestra horizontalmente entre y verticalmente por encima de las torres. Una línea desde la torre izquierda hasta el celular tiene una longitud de 5050 pies, y forma un ángulo con horizontal de theta. Una línea desde la torre derecha hasta el celular tiene una longitud de 2420 pies.$ o el ángulo$\theta$.

\[{2420^2} = {6000^2} + {5050^2} - 2(5050)(6000)\cos (\theta )\nonumber\]
\[5856400 = 61501500 - 60600000\cos (\theta )\nonumber\]
\[- 554646100 = - 60600000\cos (\theta )\nonumber\]
\[\cos (\theta ) = \dfrac-554646100-60600000 = 0.9183\nonumber\]
\[\theta = {\cos ^{ - 1}}(0.9183) = 23.328^\circ \nonumber\]

Usando este ángulo, podríamos usar triángulos rectos para encontrar la posición del celular en relación con la torre occidental. 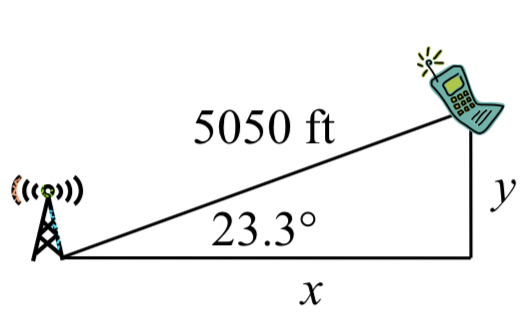$Se muestra el triángulo derecho, con una torre en la esquina inferior izquierda, ángulo recto en la parte inferior derecha y celular en la esquina superior derecha. La hipotenusa de torre a celular tiene una longitud de 5050 pies. La pata horizontal está etiquetada x y la pata vertical está etiquetada con y. El ángulo inferior izquierdo es de 23.3 grados.$

\[\cos (23.328^\circ ) = \dfrac{x}5050\nonumber\]
\[x = 5050\cos (23.328^\circ ) \approx 4637.2\text{ feet}\nonumber\]
\[\sin (23.328^\circ ) = \dfrac{y}5050\nonumber\]
\[y = 5050\sin (23.328^\circ ) \approx 1999.8\text{ feet}\nonumber\]

Estás a 5050 pies de la torre y$23.328^\circ $ al norte del este (o, equivalentemente, 66.672° al este del norte). Específicamente, estás a unos 4637 pies al este y 2000 pies al norte de la primera torre.

Ten en cuenta que si no sabías si estabas al norte o al sur de las torres, nuestros cálculos habrían dado dos posibles ubicaciones, una al norte de la carretera y otra al sur. Para resolver esta ambigüedad en situaciones del mundo real, localizar una posición mediante triangulación requiere una señal de una tercera torre.

Ejemplo$\PageIndex{10}$

Para medir la altura de un cerro, una mujer mide el ángulo de elevación a la cima del cerro para ser de 24 grados. Luego se mueve hacia atrás 200 pies y mide el ángulo de elevación para ser de 22 grados. Encuentra la altura del cerro.

Solución

Al igual que con muchos problemas de esta naturaleza, será útil dibujar un cuadro.

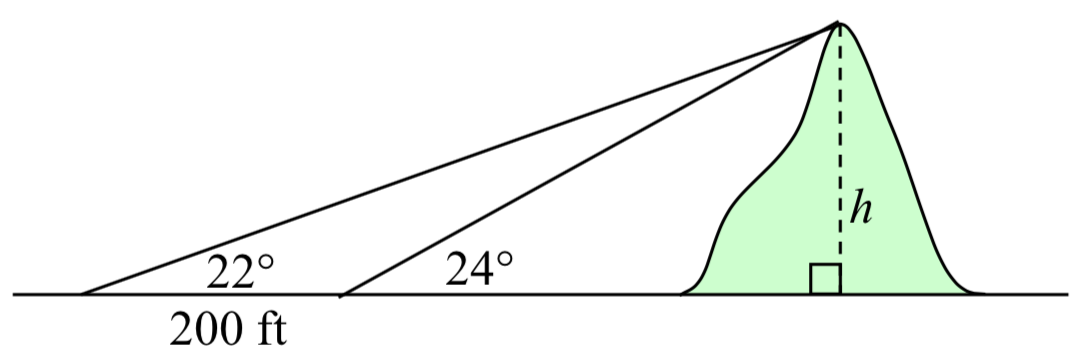
$Se muestra un cerro con altura h. Desde lo alto, se dibujan dos líneas hasta puntos en el suelo a la izquierda del cerro. La distancia entre los dos puntos en el suelo es de 200 pies. El ángulo de la primera línea es de 22 grados y el ángulo de la segunda línea es de 24 grados.$

Observe que aquí se forman tres triángulos: el triángulo recto que incluye la altura$h$ y el ángulo de 22 grados, el triángulo recto que incluye la altura$h$ y el ángulo de 24 grados, y el triángulo obtuso (no derecho) que incluye el lado de 200 pies. Dado que este es el triángulo para el que más información tenemos, comenzaremos con él. Puede parecer extraño trabajar con este triángulo ya que no incluye el lado deseado$h$, pero todavía no tenemos suficiente información para trabajar con ninguno de los triángulos rectos.

Podemos encontrar el ángulo obtuso del triángulo, ya que éste y el ángulo de 24 grados completan una línea recta, un ángulo de 180 grados. El ángulo obtuso debe ser$180^{\circ} - 24^{\circ} = 156^{\circ}$. A partir de esto, podemos determinar que el tercer ángulo es$2^{\circ}$. Sabemos que un lado es de 200 pies, y su ángulo correspondiente es$2^{\circ}$, por lo que al introducir una variable temporal$x$ para uno de los otros lados (como se muestra a continuación), podemos usar la Ley de los Sinos para resolver para esta longitud$x$.

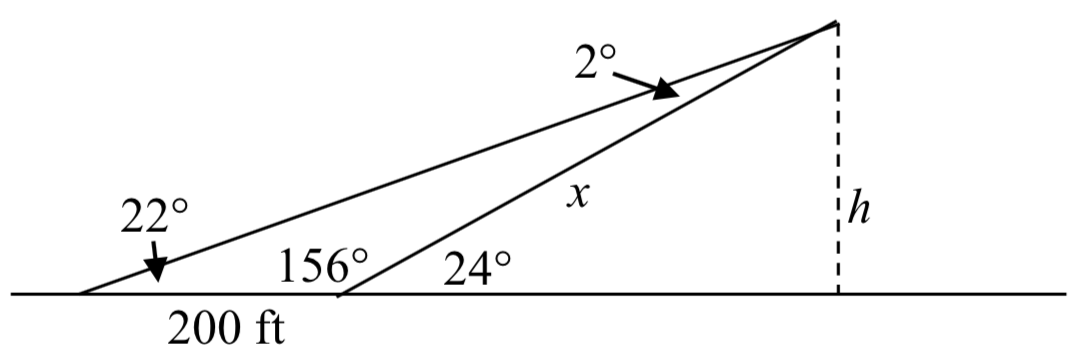
$Se muestra un eje horizontal. Se muestran dos líneas, una a 22 grados y la segunda a 24 grados, con la distancia entre donde se encuentran el eje horizontal etiquetada como 200 pies. Las dos líneas se encuentran en un punto, y una longitud de línea vertical discontinua h se dibuja hacia abajo hasta el eje horizontal. La línea en ángulo 24 grados tiene longitud etiquetada x. Las dos líneas en ángulo y el eje horizontal forman un triángulo no recto, con un lado 22 grados, el segundo ángulo 156 grados, el suplemento de 24 grados, y el tercer ángulo en la parte superior de 2 grados.$

\[\dfrac{x}{\sin (22^\circ )} = \dfrac{200}{\sin (2^\circ )}\nonumber\]Establecer la Ley de Sines
\[x = \sin (22^\circ )\dfrac{200}{\sin (2^\circ )}\nonumber\] aislando el$x$ valor
\[x = 2146.77\text{ ft}\nonumber\]

Ahora que sabemos$x$, podemos usar propiedades de triángulo rectángulo para resolver$h$.

\[\sin (24^\circ ) = \dfrac{\rm{opposite}}{\rm{hypotenuse}} = \dfrac{h}{x} = \dfrac{h}{2146.77}\nonumber\]
\[h = 2146.77\sin (24^\circ ) = 873.17\text{ ft}\nonumber\]El cerro tiene 873 pies de altura.

Temas Importantes de esta Sección

Ley de Sinos
Resolviendo para lados
Resolviendo para ángulos Caso
ambiguo, 0, 1 o 2 soluciones
Ley de Cosinos
Resolviendo para lados
Resolviendo para ángulos
Teorema Generalizado de Pitágoras