8.5.1: Producto Dot (Ejercicio)

Última actualización
Guardar como PDF

Page ID: 116933

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

ejercicios de la sección 8.5

Dos vectores se describen por su magnitud y dirección en posición estándar. Encuentra el producto punto de los vectores.

1. Magnitud: 6, Dirección:$45^{\circ}$; Magnitud: 10, Dirección:$120^{\circ}$

2. Magnitud: 8, Dirección:$220^{\circ}$; Magnitud: 7, Dirección:$305^{\circ}$

Encuentra el producto punto de cada par de vectores.

3. $\langle 0, 4 \rangle; \langle -3, 0 \rangle$

4. $\langle 6, 5 \rangle; \langle 3, 7 \rangle$

5. $\langle -2, 1 \rangle; \langle -10, 13 \rangle$

6. $\langle 2, -5 \rangle; \langle 8, -4 \rangle$

Encuentra el ángulo entre los vectores

7. $\langle 0, 4 \rangle; \langle -3, 0 \rangle$

8. $\langle 6, 5 \rangle; \langle 3, 7 \rangle$

9. $\langle 2, 4 \rangle; \langle 1, -3 \rangle$

10. $\langle -4, 1 \rangle; \langle 8, -2 \rangle$

11. $\langle 4, 2 \rangle; \langle 8, 4 \rangle$

12. $\langle 5, 3 \rangle; \langle -6, 10 \rangle$

13. Encuentra un valor para$k$ eso$\langle 2, 7 \rangle$ y$\langle k, 4 \rangle$ será ortogonal.

14. Encuentra un valor para$k$ eso$\langle -3, 5 \rangle$ y$\langle 2, k \rangle$ será ortogonal.

15. Encuentra la magnitud de la proyección de$\langle 8, -4 \rangle$ sobre$\langle 1, -3 \rangle$.

16. Encuentra la magnitud de la proyección de$\langle 2, 7 \rangle$ sobre$\langle 4, 5 \rangle$.

17. Encuentra la proyección de$\langle -6, 10 \rangle$ sobre$\langle 1, -3 \rangle$.

18. Encuentra la proyección de$\langle 0, 4 \rangle$ sobre$\langle 3, 7 \rangle$.

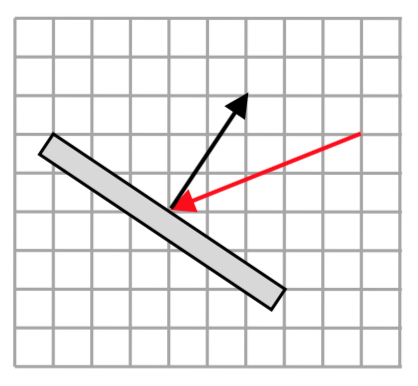
19. Un científico necesita determinar el ángulo de reflexión cuando un láser golpea un espejo. La imagen muestra el vector que representa el rayo láser, y un vector que es ortogonal al espejo. Encuentra el ángulo agudo entre estos, el ángulo de reflexión.

$2019-07-22 3.53.59.png$

20. Un triángulo tiene coordenadas en$A$: (1,4),$B$: (2,7) y$C$: (4,2). Encuentra el ángulo en el punto$B$.

21. Una embarcación queda atrapada detrás de un tronco paralelo al muelle. Solo requiere 10 libras de fuerza para tirar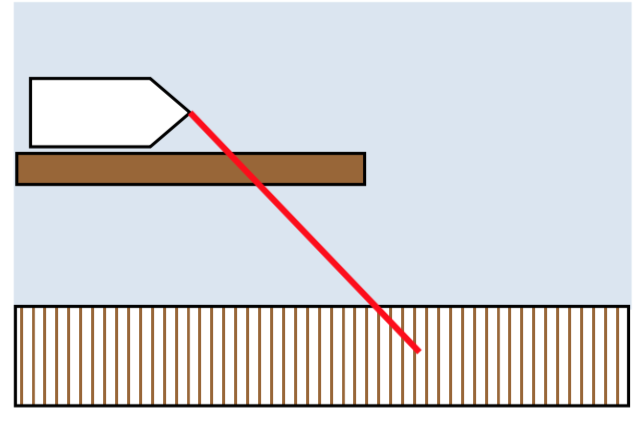 $2019-07-22 3.5.14.png$ del bote directamente hacia ti, pero debido al tronco, tendrás que tirar en$45^{\circ}$ ángulo. ¿Con cuánta fuerza tendrás que tirar? (Vamos a suponer que el tronco es muy viscosa y no aporta ninguna resistencia adicional).

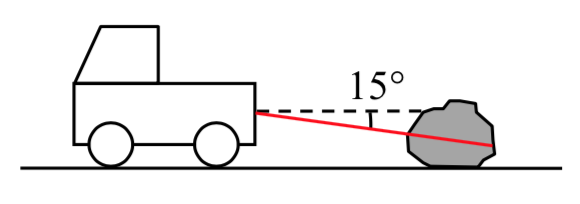
22. Una gran roca necesita ser arrastrada a una nueva posición. Si se tira directamente horizontalmente, la roca requeriría 400 libras de fuerza de tracción para moverse. Tenemos que tirar de la roca usando una cuerda atada a la parte trasera de un camión grande, formando un$15^{\circ}$ ángulo desde el suelo. ¿Con cuánta fuerza necesitará tirar el camión?

$2019-07-22 3.56.36.png$

23. Encuentra el trabajo realizado contra la gravedad empujando un carro de 20 libras 10 pies hacia arriba por una rampa que está$10^{\circ}$ por encima de la horizontal. Supongamos que no hay fricción, por lo que la única fuerza es de 20 libras hacia abajo debido a la gravedad.

24. Encuentra el trabajo realizado contra la gravedad empujando un carro de 30 libras 15 pies hacia arriba por una rampa que está$8^{\circ}$ por encima de la horizontal. Supongamos que no hay fricción, por lo que la única fuerza es de 30 libras hacia abajo debido a la gravedad.

25. Se tira de un objeto hacia la parte superior de una rampa de 40 pies que forma un$10^{\circ}$ ángulo con el suelo. Se tira por cuerda ejerciendo una fuerza de 120 libras en un$35^{\circ}$ ángulo relativo al suelo. Encuentra el trabajo realizado.

26. Se tira de un objeto hacia la parte superior de una rampa de 30 pies que forma un$20^{\circ}$ ángulo con el suelo. Se tira por cuerda ejerciendo una fuerza de 80 libras en un$30^{\circ}$ ángulo relativo al suelo. Encuentra el trabajo realizado.

Contestar

1. $6 \cdot 10 \cdot \cos(75^{\circ}) = 15.529$

3. (0) (-3) + (4) (0) = 0

5. (-2) (-10) + (1) (13) = 33\)

7. $\cos^{-1} (\dfrac{0}{\sqrt{4}\sqrt{3}}) = 90^{\circ}$

9. $\cos^(-1)(\dfrac{(2)(1) + (4)(-3)}{\sqrt{2^2 + 4^2}\sqrt{1^2 + (-3)^2}}) = 135^{\circ}$

11. $\cos^(-1)(\dfrac{(4)(8) + (2)(4)}{\sqrt{4^2 + 8^2}\sqrt{2^2 + 4^2}}) = 0^{\circ}$

13. $(2)(k) + (7)(4) = 0, k = -14$

15. $\dfrac{(8)(1) + (-4)(-3)}{\sqrt{1^2 + (-3)^2}} = 6.325$

17. $(\dfrac{(-6)(1) + (10)(-3)}{\sqrt{1^2 + (-3)^2}}^2) \langle 1, -3 \rangle = \langle -3.6, 10.8 \rangle$

19. Los vectores son$\langle 2, 3 \rangle$ y$\langle -5, -2 \rangle$. El ángulo agudo entre los vectores es$34.509^{\circ}$

21. 14.142 libras

23. $\langle 10\cos(10^{\circ}), 10\sin(10^{\circ}) \rangle \cdot \langle 0, -20 \rangle$, entonces 34.7296 ft-lbs

25. $40 \cdot 120 \cdot \cos(25^{\circ}) = 4350.277$ft-lbs