8.5: Producto Dot

Última actualización
Guardar como PDF

Page ID: 116924

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ahora que podemos sumar, restar y escalar vectores, tal vez se esté preguntando si podemos multiplicar vectores. Resulta que hay dos formas diferentes de multiplicar vectores, una que da como resultado un número, y otra que da como resultado un vector. En esta sección, nos centraremos en el primero, llamado producto punto o producto escalar, ya que produce un único valor numérico (un escalar). Empezaremos con cierta motivación.

En física, a menudo queremos saber cuánta fuerza está actuando en la dirección del movimiento. Para determinar esto, necesitamos conocer el ángulo entre la dirección de la fuerza y la dirección del movimiento. De igual manera, en los gráficos por computadora, el sistema de iluminación determina qué tan brillante debe ser un triángulo en el objeto en función del ángulo entre el objeto y la dirección de la luz. En ambas aplicaciones, nos interesa el ángulo entre los vectores, así que comencemos ahí.

Supongamos que tenemos dos vectores,

\[\vec{a} = \langle a_1, a_2 \rangle\quad \text{and} \quad \vec{b} = \langle b_1, b_2 \rangle.\nonumber\]

Usando nuestras conversiones de coordenadas polares, podríamos escribir

\[\vec{a} = \langle |\vec{a}|\cos(\alpha), |\vec{a}|\sin(\alpha) \rangle\nonumber\]

\[\vec{b} = \langle |\vec{b}|\cos(\beta), |\vec{b}|\sin(\beta) \rangle\nonumber\]

Ahora bien, si conociéramos el ángulo$\alpha$ y$\beta$, no tendríamos mucho trabajo por hacer = el ángulo entre los vectores sería$\theta = \alpha = \beta$.

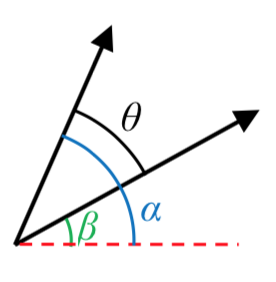
$Se muestran dos vectores: el primero en un ángulo de alfa, el segundo en un ángulo de beta. El ángulo entre los vectores es theta.$

Si bien ciertamente podríamos usar algunas tangentes inversas para encontrar los dos ángulos, sería genial si pudiéramos encontrar una manera de determinar el ángulo entre el vector solo a partir de los componentes del vector.

Para ayudarnos a manipular$\theta = \alpha - \beta$, podríamos intentar introducir una función trigonométrica:

\[\cos(\theta) = \cos(\alpha - \beta)\nonumber\]

Ahora podemos aplicar la diferencia de ángulos de identidad

\[\cos(\theta) = \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)\nonumber\]

Ahora$a_1 = |\vec{a}|\cos(\alpha)$, así$\cos(\alpha) = \dfrac{a_1}{|\vec{a}|}$, e igualmente para los otros tres componentes.

Haciendo esas sustituciones,

\[\cos(\theta) = \dfrac{a_1}{|\vec{a}|} \dfrac{b_1}{|\vec{b}|} + \dfrac{a_2}{|\vec{a}|} \dfrac{b_2}{|\vec{b}|} = \dfrac{a_1 b_1 + a_2 b_2}{|\vec{a}| |\vec{b}|}\nonumber\]
\[|\vec{a}||\vec{b}| \cos(\theta) = a_1 b_1 + a_2 b_2\nonumber\]

Observe que la expresión a la derecha es un cálculo muy sencillo basado en los componentes de los vectores. Surge con tanta frecuencia que lo definimos como el producto de punto de los dos vectores, anotado por un punto. Esto nos da dos definiciones del producto punto.

DEFINICIONES DEL PRODUCTO DOT

\[\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2\quad\text{ Component definition}\]

\[\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta)\quad\text{ Geometric definition}\]

La primera definición,$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2$, nos da una forma sencilla de calcular el producto punto a partir de componentes. La segunda definición,$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta)$, nos da una interpretación geométrica del producto punto, y nos da una manera de encontrar el ángulo entre dos vectores, como deseábamos.

Ejemplo$\PageIndex{1}$

Encuentra el producto punto$\langle 3, -2 \rangle \cdot \langle 5, 1 \rangle$.

Solución

Usando la primera definición, podemos calcular el producto punto multiplicando los$x$ componentes y agregándolo al producto de los$y$ componentes.

\[\langle 3, -2 \rangle \cdot \langle 5, 1 \rangle = (3)(5) + (-2) (1) = 15 - 2 = 13\nonumber\]

Ejemplo$\PageIndex{2}$

encontrar el producto punto de los dos vectores mostrados.

Solución

De inmediato podemos ver que las magnitudes de los dos vectores son 7 y 6, rápidamente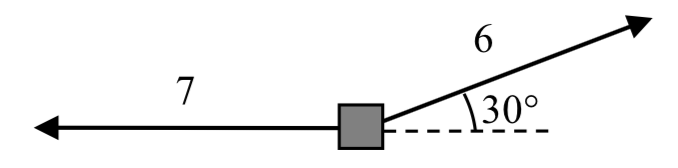 $Un objeto se muestra en el medio con dos vectores que provienen de él: Un vector de longitud 7 apuntando a la izquierda, y un vector de longitud 6 a 30 grados.$ calculamos que el ángulo entre los vectores es$150^{\circ}$. Usando la definición geométrica del producto de punto,

\[\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta) = (6)(7) \cos(150^{\circ}) = 42 \cdot \dfrac{\sqrt{3}}{2} = 21\sqrt{3}\nonumber\]

Ejercicio$\PageIndex{1}$

Calcular el producto punto$\langle -7, 3 \rangle \cdot \langle -2, -6 \rangle $

Contestar: \[\langle -7, 3 \rangle \cdot \langle -2, -6 \rangle = (-7)(-2) + (3) (-6) = 14 - 18 = -4\nonumber\]

Ahora podemos volver a nuestro objetivo de encontrar el ángulo entre vectores.

Ejemplo$\PageIndex{3}$

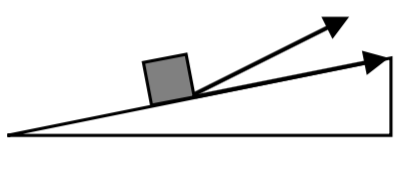$Un objeto se muestra en una rampa inclinada. Se muestran dos vectores provenientes del objeto: uno paralelo a la rampa, y el otro apuntando en ángulo por encima de la rampa.$ Un objeto está siendo jalado por una rampa en la dirección$\langle 5,1 \rangle$ por una cuerda que tira en la dirección$\langle 4,2 \rangle$. ¿Cuál es el ángulo entre la cuerda y la rampa?

Solución

Usando la forma del componente, podemos calcular fácilmente el producto de punto.

\[\vec{a} \cdot \vec{b} = \langle 5, 1 \rangle \cdot \langle 4, 2 \rangle = (5)(4) + (1)(2) = 20 + 2 = 22\nonumber\]

También podemos calcular la magnitud de cada vector.

\[|\vec{a}| = \sqrt{5^2 + 1^2} = \sqrt{26}\quad |\vec{b}| = \sqrt{4^2 + 2^2} = \sqrt{20}\nonumber\]

Sustituyendo estos valores en la definición geométrica, podemos resolver para el ángulo entre los vectores.

\[\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta)\nonumber\]
\[22 = \sqrt{26}{20} \cos (\theta)\nonumber\]
\[\theta = \cos^{-1} (\dfrac{22}{\sqrt{26} \sqrt{20}}) \approx 15. 255^{\circ}\nonumber\]

Ejemplo$\PageIndex{4}$

Calcular el ángulo entre los vectores$\langle 6, 4 \rangle$ y$\langle -2, 3 \rangle$.

Solución

Calcular el producto punto,$\langle 6, 4 \rangle \cdot \langle -2, 3 \rangle = (6)(-2) + (4)(3) = -12 + 12 = 0$

Ni siquiera necesitamos calcular las magnitudes en este caso ya que el producto punto es 0.

\[\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta)\nonumber\]
\[0 = |\vec{a}| |\vec{b}| \cos(\theta)\nonumber\]
\[\theta = \cos^{-1} (\dfrac{0}{|\vec{a}||\vec{b}|}) = \cos^{-1} (0) = 90^{\circ}\nonumber\]

Con el producto punto igual a cero, como en el último ejemplo, el ángulo entre los vectores siempre será$90^{\circ}$, indicando que los vectores son ortogonales, una forma más general de decir perpendicular. Esto nos da una manera rápida de verificar si los vectores son ortogonales. Además, si el producto punto es positivo, entonces el interior del coseno inverso será positivo, dando un ángulo menor que$90^{\circ}$. Un producto de punto negativo conducirá entonces a un ángulo mayor que$90^{\circ}$.

SEÑAL DEL PRODUCTO DOT

Si el producto punto es:

Cero Los vectores son ortogonales (perpendiculares).

Positivo El ángulo entre los vectores es menor que$90^{\circ}$

Negativo El ángulo entre los vectores es mayor que$90^{\circ}$

Ejercicio$\PageIndex{2}$

¿Son los vectores$\langle -7, 3 \rangle$ y$\langle -2, -6 \rangle $ ortogonales? Si no, encuentra el ángulo entre ellos.

Contestar: En el Ejercicio anterior, encontramos que el producto punto era -4, por lo que los vectores no son ortogonales. Las magnitudes de los vectores son$\sqrt{(-7)^2 + 3^2} = \sqrt{58}$ y$\sqrt{(-2)^2 + 6^2} = \sqrt{40}$. El ángulo entre los vectores será$\theta = \cos^{-1} (\dfrac{-4}{\sqrt{58}\sqrt{40}}) \approx 94.764^{\circ}$

Proyecciones

Además de encontrar el ángulo entre vectores, a veces queremos saber cuánto apunta un vector en la di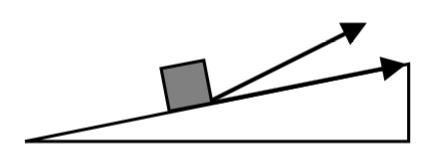 $Un objeto se muestra en una rampa inclinada. Se muestran dos vectores provenientes del objeto: uno paralelo a la rampa, y el otro apuntando en ángulo por encima de la rampa.$ rección de otro. Por ejemplo, al tirar de un objeto por una rampa, es posible que queramos saber cuánta fuerza se ejerce en la dirección del movimiento. Para determinar esto podemos usar la idea de una proyección.

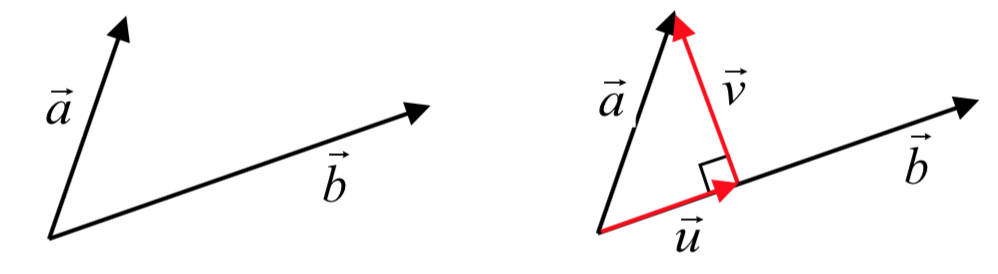
$Se muestran dos vectores a y b comenzando en el mismo punto. Desde la punta de a, se dibuja una línea hacia abajo hasta b encontrarla en ángulo recto. Un vector etiquetado como u se muestra desde el inicio de b hasta el punto donde la línea se encontró con b. Un vector v se muestra desde ese punto hasta la punta de a.$

En la imagen de arriba,$\vec{u}$ es una proyección de$\vec{a}$ sobre$\vec{b}$. En otras palabras, es la porción de$\vec{a}$ que apunta en la misma dirección que$\vec{b}$.

Para encontrar la longitud de$\vec{u}$, podríamos notar que es un lado de un triángulo rectángulo. Si definimos$\theta$ que es el ángulo entre$\vec{a}$ y$\vec{u}$, entonces$\cos(\theta) = \dfrac{|\vec{u}|}{|\vec{a}|}$, así$|\vec{a}|\cos (\theta)= |\vec{u}|$.

Si bien podríamos encontrar el ángulo entre los vectores para determinar esta magnitud, podríamos saltarnos algunos pasos usando el producto punto directamente. Ya que$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos(\theta)$,$|\vec{a}| \cos(\theta) = \dfrac{\vec{a} \cdot \vec{b}}{|vec{b}|}$. Usando esto, podemos rewrtie$|\vec{u}| = |\vec{a}| \cos(\theta)$ como$|\vec{u}| = \dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$. Esto nos da la longitud de la proyección, a veces denotada como$comp_{\vec{b}}\vec{a} = |\vec{u}| = \dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$.

Para encontrar el vector$\vec{u}$ en sí, primero podríamos escalar$\vec{b}$ a un vector unitario con longitud 1:$\dfrac{\vec{b}}{|\vec{b}|}$.

Multiplicando esto por la longitud de la proyección dará un vector en la dirección de$\vec{b}$ pero con la longitud correcta.

\[proj_{\vec{b}} \vec{a} = |\vec{u}| \dfrac{\vec{b}}{|\vec{b}|} = (\dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|}) \dfrac{\vec{b}}{|\vec{b}|} = (\dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2}) \vec{b}\nonumber\]

VECTOR PROYECCIÓN

La proyección del vector$\vec{a}$ sobre$\vec{b}$ es\[proj_{\vec{b}} \vec{a} = (\dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2}) \vec{b}\]

La magnitud de la proyección es\[comp_{\vec{b}} \vec{a} = \dfrac{\vec{a} \cdot \vec{b}}{|vec{b}|}\]

Ejemplo$\PageIndex{5}$

Encuentra la proyección del vector$\langle 3, -2 \rangle$ sobre el vector$\langle 8, 6 \rangle$.

Solución

Necesitaremos conocer el producto punto de los vectores y la magnitud del vector sobre el que estamos proyectando. 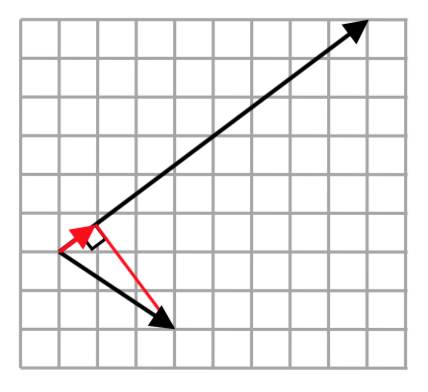$Se muestran dos vectores comenzando en el mismo punto. Desde la punta de uno, se dibuja una línea hacia abajo hacia la otra, encontrándola en ángulo recto. Eso forma un triángulo rectángulo, y las dos patas se dibujan como vectores.$

\[\langle 3, -2 \rangle \cdot \langle 8, 6 \rangle = (3)(8) + (-2)(6) = 24 - 12 = 12\nonumber\]
\[|\langle 8, 6 \rangle| = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10\nonumber\]

La magnitud de la proyección será$\dfrac{\langle 3, -2 \rangle \cdot \langle 8, 6 \rangle}{|\langle 8, 6 \rangle|} = \dfrac{12}{10} = \dfrac{6}{5}$.

Para encontrar el vector de proyección en sí, multiplicaríamos esa magnitud por$\langle 8,6 \rangle$ escalar a un vector unitario.

\[\dfrac{6}{5} \dfrac{\langle 8, 6 \rangle}{|\langle 8, 6 \rangle|} = \dfrac{6}{5} \dfrac{\langle 8, 6 \rangle}{10} = \dfrac{6}{50} \langle 8, 6 \rangle = \langle \dfrac{48}{50}, \dfrac{36}{50} \rangle = \langle \dfrac{24}{25}, \dfrac{18}{25} \rangle\nonumber\]

Con base en el boceto anterior, esta respuesta parece razonable.

Ejercicio$\PageIndex{3}$

Encuentra el componente del vector$\langle -4, 4 \rangle $ que es$orthogonal$ al vector$\langle -8, 4\rangle$

Contestar

Queremos encontrar el componente de$\langle -3, 4 \rangle$ eso es$orthogonal$ al vector$\langle -8, 4 \rangle$. En la 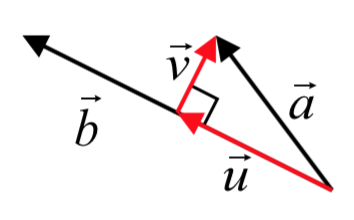$Dos vectores a y b se dibujan del mismo punto. Una línea desde la punta de a hasta el vector b, reuniéndola en ángulo recto, forma un triángulo rectángulo. Las patas están etiquetadas como vectores u y v.$ imagen de la derecha, ese componente es vector$\vec{v}$. Observe eso$\vec{u} + \vec{v} = \vec{a}$, así que si podemos encontrar el vector de proyección, podemos encontrar$\vec{v}$.

\[\vec{u} = proj_{\vec{b}} \vec{a} = (\dfrac{\vec{a} \cdot \vec{b}}{|\vec{b}|^2}) \vec{b} = (\dfrac{\langle -3, 4 \rangle \cdot \langle -8, 4 \rangle}{(\sqrt{(-8)^2 + 4^2})^2}) \langle -8, 4 \rangle = \dfrac{}{} \langle -8, 4 \rangle = \langle -4, 2 \rangle\nonumber\]

Ahora podemos resolver$\vec{u} + \vec{v} = \vec{a}$ para$\vec{v}$.

\[\vec{v} = \vec{a} - \vec{u} = \langle -3, 4 \rangle - \langle -4, 2 \rangle = \langle 1, 2 \rangle\nonumber\]

Trabajo

En física, cuando una fuerza constante hace que un objeto se mueva, el trabajo mecánico realizado por esa fuerza es producto de la fuerza y la distancia que se mueve el objeto. Sin embargo, solo consideramos la porción de fuerza que está actuando en la dirección del movimiento.

Esto es simplemente la magnitud de la proyección del vector de fuerza sobre el vector de distancia,$\dfrac{\vec{F} \cdot \vec{d}}{|\vec{d}|}$. El trabajo realizado es el producto de ese componente de fuerza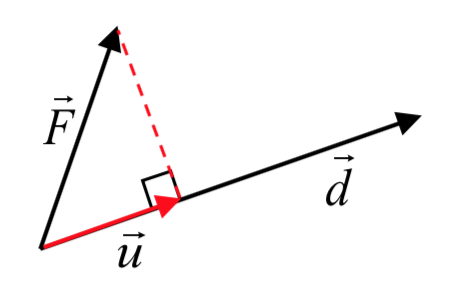 $Se dibujan dos vectores F y d comenzando en el mismo punto. Desde la punta de F se dibuja una línea al vector d, encontrándolo en ángulo recto. La parte de d desde el inicio hasta donde se encuentra esta línea se etiqueta como vector u.$ multiplicado por la distancia movida, la magnitud del vector de distancia.

$Work = (\dfrac{\vec{F} \cdot \vec{d}}{|\vec{d}|})|\vec{d}| = \vec{F} \cdot \vec{d}$

Resulta que el trabajo es simplemente el producto puntual del vector de fuerza y el vector de distancia.

TRABAJAR

Cuando una fuerza$\vec{F}$ hace que un objeto se mueva cierta distancia$\vec{d}$, el trabajo realizado es$Work = \vec{F} \cdot \vec{d}$

Ejemplo$\PageIndex{6}$

Se tira de un carro de 20 pies aplicando una fuerza de 30 libras sobre una cuerda sujeta en un ángulo de 30 grados. ¿Cuánto trabajo se realiza?

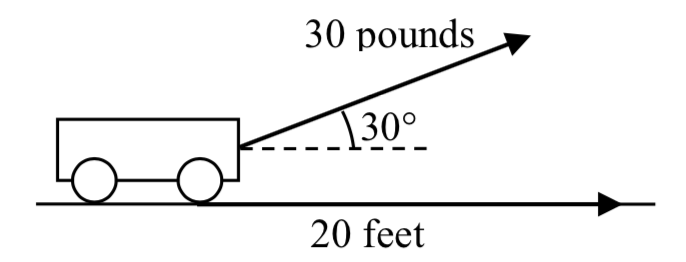
$Se muestra un carro, con dos vectores que provienen de él: un vector apuntando a la derecha etiquetado 20 pies, y un vector a 30 grados etiquetado 30 libras.$

Solución

Dado que el trabajo es simplemente el producto dot, podemos aprovechar la definición geométrica del producto dot en este caso.

\[Work = \vec{F} \cdot \vec{d} = |\vec{F}| \cdot |\vec{d}| \cos (\theta) = (30) (20) \cos (30^{\circ}) \approx 519.615\text{ ft-lbs}\nonumber\]

Ejercicio$\PageIndex{4}$

Encuentra el trabajo hacia abajo moviendo un objeto desde el punto (1, 5) hasta (9, 14) por el vector de fuerza$\vec{F} = \langle 3, 2 \rangle$.

Contestar

El vector de distancia es$\langle 9 - 1, 14 -5 \rangle = \langle 8, 9 \rangle$.

El trabajo es el producto punto:\[Work = \vec{F} \cdot \vec{d} = \langle 3, 2 \rangle \cdot \langle 8, 9 \rangle = 24 + 18 = 42\nonumber\]

Temas Importantes de esta Sección

Calcular producto de punto
Usando definición de componente
Uso de definición geométrica
Encuentra el ángulo entre dos vectores
Signo del producto punto
Proyecciones
Trabajo