8.6: Ecuaciones paramétricas

Última actualización
Guardar como PDF

Page ID: 116907

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Muchas formas, incluso aquellas tan simples como los círculos, no se pueden representar como una ecuación donde$y$ es una función de$x$. Consideremos, por ejemplo, el camino que sigue una luna mientras orbita alrededor de un planeta, que simultáneamente gira alrededor de un sol. En algunos casos, las ecuaciones polares proporcionan una manera de representar tal camino. En otros, necesitamos un enfoque más versátil que nos permita representar tanto las$x$$y$ coordenadas como en términos de una tercera variable, o parámetro.

Definición: Ecuaciones paramétricas

Un sistema de ecuaciones paramétricas es un par de funciones$x(t)$ y$y(t)$ en el que las$y$ coordenadas$x$ y son la salida, representada en términos de un tercer parámetro de entrada,$t$.

Ejemplo$\PageIndex{1}$

Moviéndose a una velocidad constante, un objeto se mueve a una velocidad constante a lo largo de una trayectoria recta desde las coordenadas (-5, 3) hasta las coordenadas (3, -1) en 4 segundos, donde las coordenadas se miden en metros. Encuentra ecuaciones paramétricas para la posición del objeto.

Solución

La$x$ coordenada del objeto inicia en -5 metros, y va a +3 metros, esto significa que la$x$ dirección ha cambiado en 8 metros en 4 segundos, dándonos una tasa de 2 metros por segundo. Ahora podemos escribir la$x$ coordenada como una función lineal con respecto al tiempo,$t$,$x(t) = −5 + 2t$. De igual manera, el$y$ valor inicia en 3 y va a -1, dando un cambio de$y$ valor de 4 metros, es decir, los$y$ valores han disminuido en 4 metros en 4 segundos, para una tasa de -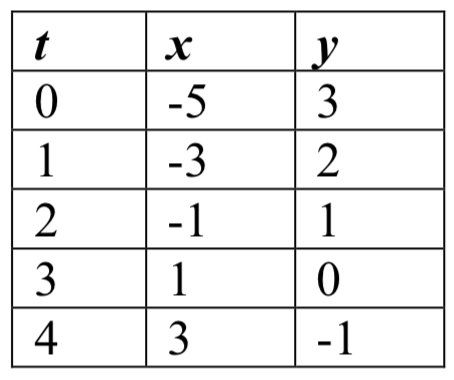 $2019-07-22 4.04.51.png$ 1 metro por nd, dando ecuación$y(t)=3−t$. Juntas, estas son las ecuaciones paramétricas para la posición del objeto:

\[x(t) = -5 + 2t\nonumber\]
\[y(t) = 3 - t\nonumber\]

Usando estas ecuaciones, podemos construir una tabla de$t$,$x$, y$y$ valores. Por el contexto, nos limitamos a$t$ valores no negativos para este ejemplo, pero en general puedes usar cualquier valor.

A partir de esta tabla, podríamos crear tres posibles gráficas: una gráfica de$x$ vs.$t$, que mostraría la posición horizontal a lo largo del tiempo, una gráfica de$y$ vs.$t$, que mostraría la posición vertical a lo largo del tiempo, o una gráfica de$y$ vs.$x$, mostrando la posición del objeto en el plano.

Posición de$x$ como una función del tiempo Posición de$y$ como una función del tiempo Posición de$y$ relativo a$x$

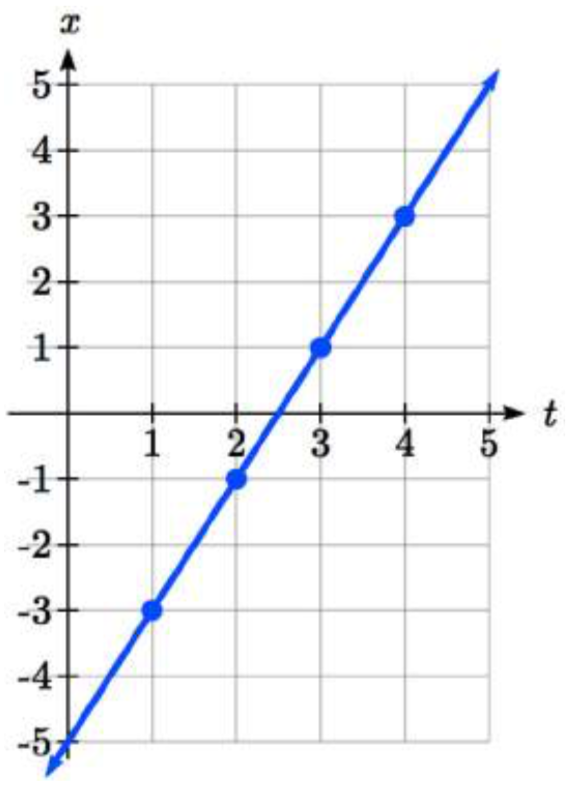
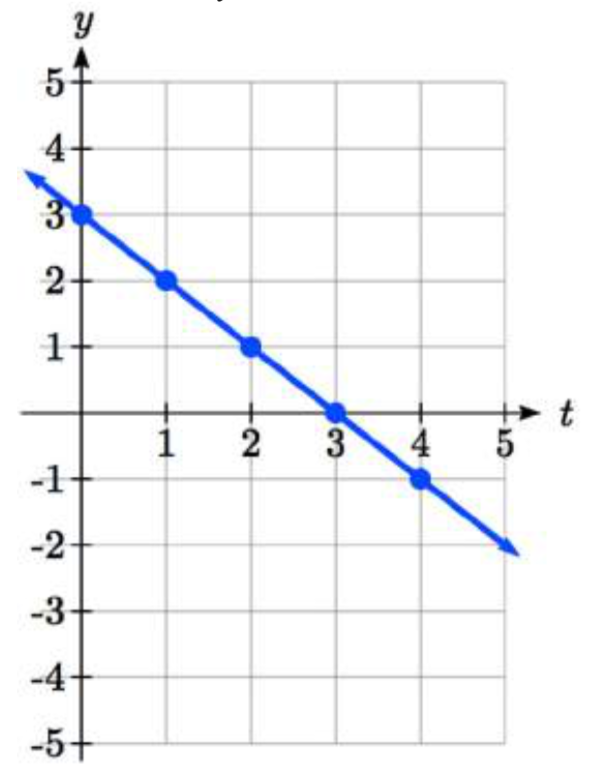
$Una gráfica con t en el eje horizontal y x en el eje vertical. Se dibuja una línea pasando por 0 coma negativa 5, 1 coma negativa 3, 2 coma negativa 1, 3 coma 1 y 4 coma 3$ $Una gráfica con t en el eje horizontal e y en el eje vertical. Se dibuja una línea pasando por 0 coma 3, 1 coma 2, 2 coma 1, 3 coma 0 y 4 coma negativa 1$ $Una gráfica con x en el eje horizontal e y en el eje vertical. Una línea pasa por negativo 5 coma 3, negativo 3 coma 2, negativo 1 coma 1, 1 coma 0 y 3 coma negativo 1. Una flecha en la gráfica indica movimiento de izquierda a derecha a lo largo de la línea.$

Observe que el parámetro$t$ no aparece explícitamente en esta tercera gráfica. En ocasiones, cuando el parámetro$t$ sí representa una cantidad como el tiempo, podríamos indicar la dirección del movimiento en la gráfica usando una flecha, como se muestra arriba.

A menudo no hay una representación paramétrica única para una curva. En el Ejemplo 1 asumimos que el objeto se movía a un ritmo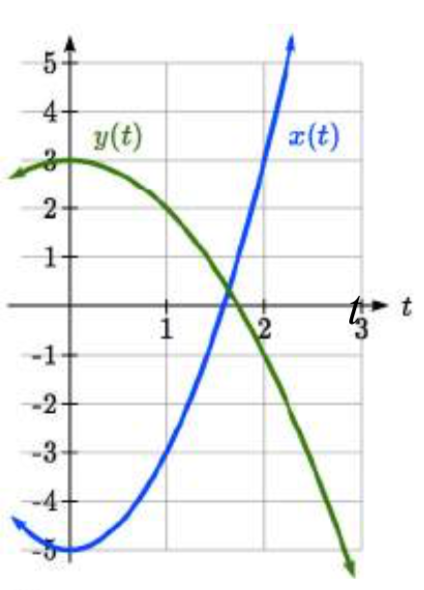 $Dos gráficas en los mismos ejes, con el eje horizontal etiquetado t. La primera etiquetada x de t es una parábola con vértice a 0 coma negativa 5 abriéndose hacia arriba pasando por 1 coma negativa 3 y 2 coma 3. La segunda etiquetada y de t es una parábola con vértice a 0 coma 3 abriendo hacia abajo pasando por 1 coma 2 y 2 coma negativa 1.$ constante a lo largo de una línea recta. Si mantuvimos la suposición sobre el camino (línea recta) pero no asumimos que la velocidad era constante, podríamos obtener un sistema como:

\[x(t) = -5 + 2t^2\nonumber\]
\[y(t) = 3 - t^2\nonumber\]

Esto comienza en (-5, 3) cuando$t = 0$ y termina en (3, -1) cuando$t = 2$. Si graficamos la$y(t)$ función$x(t)$ y por separado, podemos ver que esas ya no son lineales, pero si$y$ graficamos$x$ vs veremos que seguimos obteniendo una ruta en línea recta.

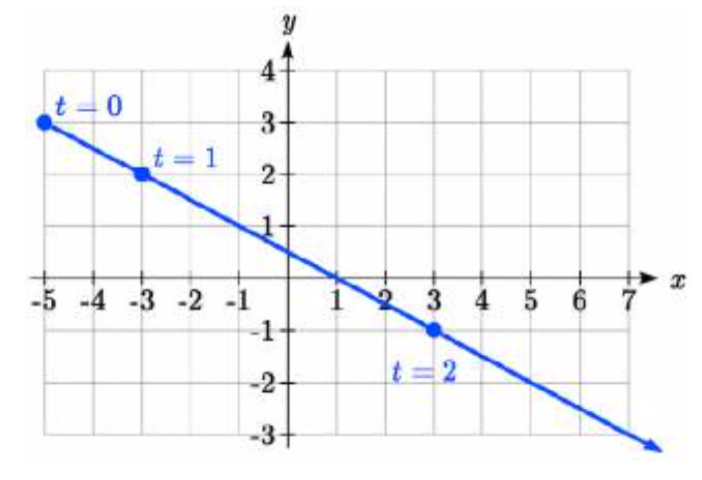
$Una gráfica con eje horizontal x y eje vertical y La gráfica muestra una línea que pasa por un punto en negativo 5 coma 3 etiquetado t igual a 0, un punto en negativo 3 coma 2 etiquetado t es igual a 1, y un punto en 3 coma negativo 1 etiquetado t igual a 2.$

Ejemplo$\PageIndex{2}$

Esbozar un gráfico de

\[x(t) = t^2 + 1\nonumber\]
\[y(t) = 2 + t\nonumber\]

Solución

Podemos comenzar por crear una tabla de valores. A partir de esta tabla, podemos trazar los puntos ($x$,$y$) en el plano, bosquejar en un gr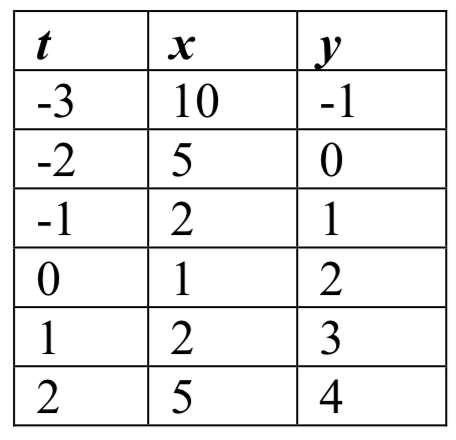 $2019-07-22 4.11.53.png$ aph áspero de la curva, e indicar la dirección del movimiento con respecto al tiempo mediante flechas.

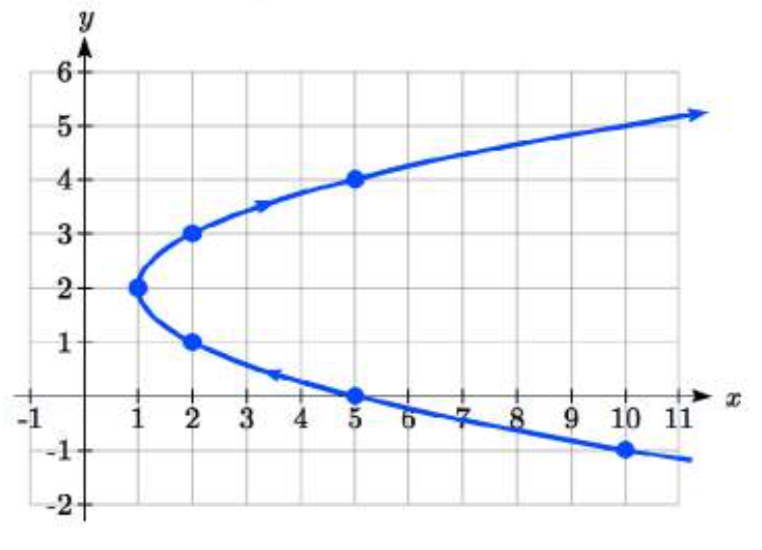
$Una gráfica con eje horizontal x y eje vertical y La gráfica es una parábola lateral, con dirección de movimiento indicada por flechas. En la dirección del movimiento la curva pasa por 10 coma negativa 1, 5 coma 0, 2 coma 1, 1 coma 2, 2 coma 3 y 5 coma 4.$

Observe que aquí las ecuaciones paramétricas describen una forma para la cual no$y$ es función de$x$. Este es un ejemplo de por qué el uso de ecuaciones paramétricas puede ser útil, ya que pueden representar dicha gráfica como un conjunto de funciones. Esta gráfica en particular también parece ser una parábola donde$x$ es función de$y$, que pronto verificaremos.

Ejemplo$\PageIndex{3}$

Esbozar un gráfico de

\[x(t) = 3\cos(t)\nonumber\]
\[y(t) = 3\sin(t)\nonumber\]

Solución

Estas ecuaciones deberían parecer familiares. Cuando aprendimos por primera vez sobre seno y coseno encontramos que las coordenadas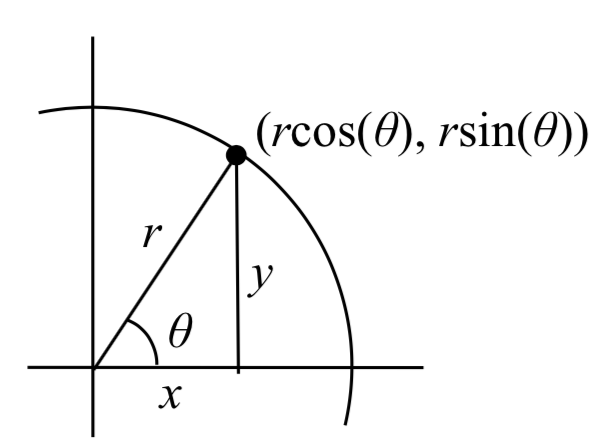 $Se muestra un radio de círculo r. En un ángulo de theta, se dibuja una línea, reuniéndose en un punto x coma y. El punto se etiqueta r coseno theta coma r seno theta.$ de un punto en un círculo de radio$r$ en un ángulo de$\theta$ serán$x = r \cos(\theta), y r \sin(\theta)$. Las ecuaciones anteriores están en la misma forma, con$r =3$, y$t$ se utilizan en lugar de$\theta$.

Esto sugiere que para cada valor de$t$, estas ecuaciones paramétricas dan un punto en un círculo de ra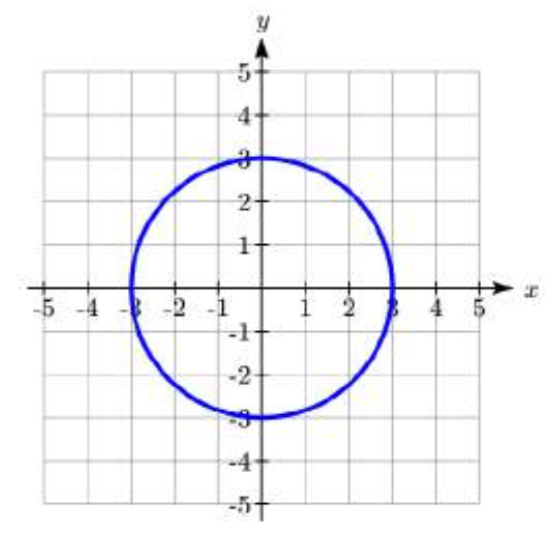 $Una gráfica de un círculo con radio 3 centrado en el origen.$ dius 3 en el ángulo correspondiente a$t$. En$t = 0$, la gráfica estaría en$x = 3\cos(0), y = 3\sin(0)$, el punto (3,0). En efecto, estas ecuaciones describen la ecuación de un círculo, dibujado en sentido antihorario.

Curiosamente, estas ecuaciones paramétricas similares también describen el círculo de radio 3:

\[x(t) = 3\sin(t)\nonumber\]
\[y(t) = 3\cos(t)\nonumber\]

La diferencia con estas ecuaciones es que la gráfica comenzaría en$x = 3\sin(0)$,$y = 3\cos(0)$, el punto (0, 3). A medida que$t$ aumenta a partir de 0, el$x$ valor aumentará, lo que indica que esta ecuación dibujaría la gráfica en sentido horario.

Si bien crear una$t-x-y$ tabla, trazar puntos y conectar los puntos con una curva suave generalmente funciona para darnos una idea aproximada de cómo es la gráfica de un sistema de ecuaciones paramétricas, generalmente es más fácil usar la tecnología para crear estas tablas y (simultáneamente) gráficas mucho más bonitas.

Ejemplo$\PageIndex{4}$

Esbozar un gráfico de$\begin{array} {rcl} {x(t)} &= & {2\cos(t)} \\ {y(t)} &= & {3\sin(t)} \end{array}$

Solución

Observe primero que esta ecuación se ve muy similar a las del ejemplo anterior, excepto que los coeficientes no son equ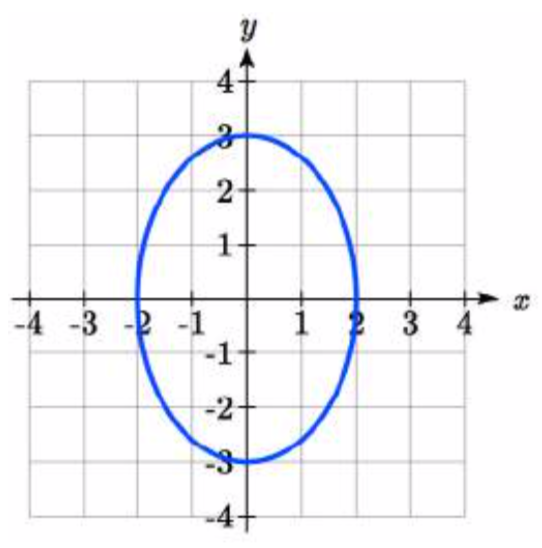 $Una gráfica de una elipse centrada en el origen, con radio horizontal 2 y radio vertical 3.$ al. Podrías adivinar que el emparejamiento de cos y pecado seguirá produciendo rotación, pero ahora$x$ variará de -2 a 2 mientras que$y$ variará de -3 a 3, creando una elipse.

Utilizando la tecnología podemos generar una gráfica de esta ecuación, verificando que efectivamente es una elipse.

Similar a graficar ecuaciones polares, debes cambiar el MODO en tu calculadora (o seleccionar ecuaciones paramétricas en tu tecnología gráfica) antes de graficar un sistema de ecuaciones paramétricas. Sabrás que has ingresado exitosamente al modo paramétrico cuando la entrada de la ecuación haya cambiado para pedir a$x(t)=$ y$y(t)=$ par de ecuaciones.

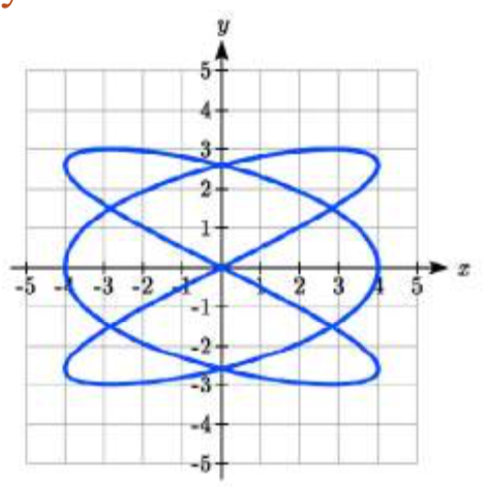
Ejercicio$\PageIndex{1}$

Esbozar una gráfica de$\begin{array} {rcl} {x(t)} &= & {4\cos(3t)} \\ {y(t)} &= & {3\sin(2t)} \end{array}$. Este es un ejemplo de una figura de Lissajous.

Contestar: $Una figura espiral repetitiva que oscila de 4 a 4 negativo en la x y negativo 3 a 3 en la y, oscilando 3 veces en la dirección x en el tiempo que tarda en oscilar dos veces en la dirección y.$

Ejemplo$\PageIndex{5}$

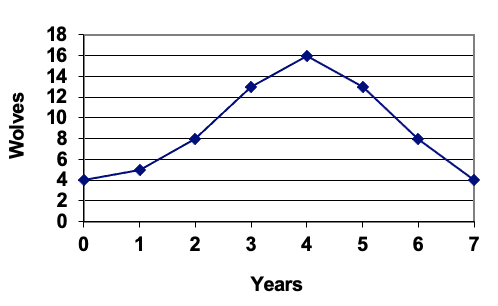
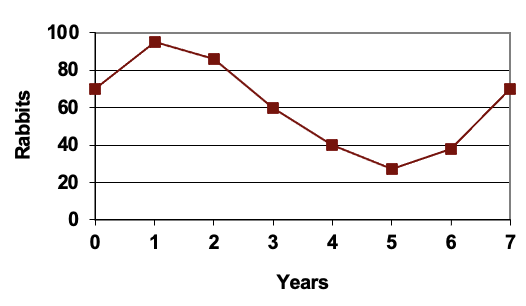
Las poblaciones de conejos y lobos en una isla a lo largo del tiempo están dadas por los gráficos a continuación. Utilice estas gráficas para bosquejar una gráfica en el plano r-w que muestre la relación entre el número de conejos y el número de lobos.

$Un gráfico de líneas con lobos rotulados verticales y horizontales etiquetados Años. La gráfica muestra datos que aumentan y luego disminuyen, incluyendo los puntos 0 coma 4, 1 coma 5 y 2 coma 8.$ $Un gráfico de líneas con Conejos rotulados verticales y horizontales etiquetados Años. La gráfica muestra datos que aumentan brevemente, disminuyen, luego vuelven a aumentar, incluyendo los puntos 0 coma 70, 1 coma 95 y 2 coma 85.$

Solución

Para cada entrada$t$, podemos determinar el número de conejos,$r$, y el número de lobos,$w$, a partir de las respectivas gráficas, para luego trazar el punto correspondiente en el$r-w$ plano.

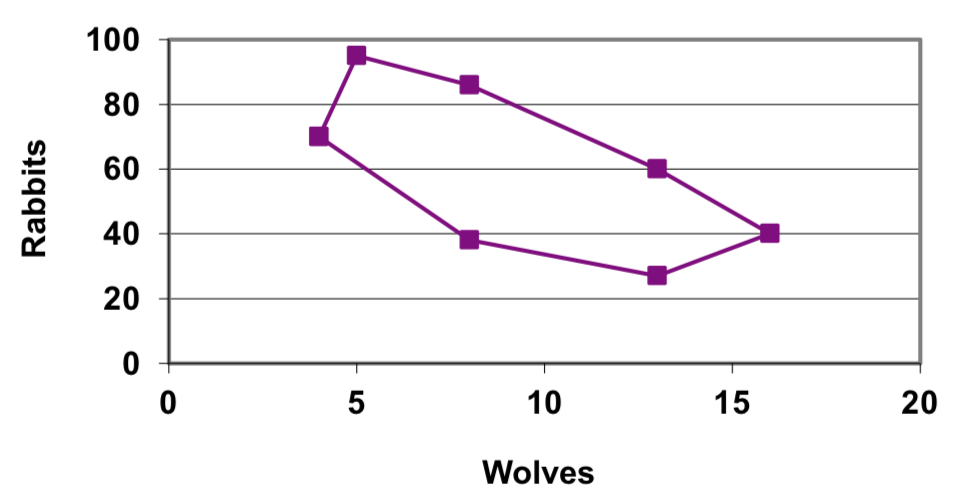
$Un gráfico de líneas, con la vertical etiquetada Conejos y la horizontal etiquetada Lobos. Se muestra una gráfica de forma ovalada, que incluye los puntos 4 coma 70, 5 coma 95 y 8 coma 85.$

Esta gráfica ayuda a revelar la interacción cíclica entre las dos poblaciones.

Conversión de paramétrico a cartesiano

En algunos casos, es posible eliminar el parámetro$t$, lo que permite escribir un par de ecuaciones paramétricas como una ecuación cartesiana.

Es más fácil hacer esto si una de las$y(t)$ funciones$x(t)$ o se puede resolver fácilmente$t$, lo que le permite luego sustituir la expresión restante en la segunda parte.

Ejemplo$\PageIndex{6}$

Escribir$\begin{array} {rcl} {x(t)} &= & {t^2 + 1} \\ {y(t)} &= & {2 + t} \end{array}$ como una ecuación cartesiana, si es posible.

Solución

Aquí, la ecuación para$y$ es lineal, por lo que es relativamente fácil de resolver$t$. Dado que la ecuación cartesiana resultante probablemente no será una función, y por conveniencia, dejamos caer la notación de función.

\[y = 2 + t\nonumber\]Resolver por$t$
\[y - 2 = t\nonumber\] Sustituir esto por$t$ en la$x$ ecuación
\[x = (y - 2)^2 + 1\nonumber\]

Observe que esta es la ecuación de una parábola con$x$ en función de$y$, con vértice en (1,2), abriéndose a la derecha. Comparando esto con la gráfica del Ejemplo 2, vemos (como era de esperar) que produce la misma gráfica en el$x-y$ plano que las ecuaciones paramétricas originales.

Ejercicio$\PageIndex{2}$

Escribir$\begin{array} {rcl} {x(t)} &= & {t^3} \\ {y(t)} &= & {t^6} \end{array}$ como una ecuación cartesiana, si es posible.

Contestar: \[y = (t^3)^2\text{, so }y = x^2\nonumber\]

Ejemplo$\PageIndex{7}$

Escribir$\begin{array} {x(t)} &= & {\sqrt{t} + 2} \\ {y(t)} &= & {\text{log}(t)} \end{array}$ como una ecuación cartesiana, si es posible.

Solución

Podríamos resolver ya sea la primera o la segunda ecuación para$t$. Resolviendo el primero,

\[x = \sqrt{t} + 2\nonumber\]
\[x - 2 = \sqrt{t}\nonumber\]Cuadrar ambos lados
\[(x - 2)^2 = t\nonumber\] Sustituir en la$y$ ecuación
\[y = \text{log} ((x - 2)^2)\nonumber\]

Dado que la ecuación paramétrica solo se define para$t > 0$, esta ecuación cartesiana es equivalente a la ecuación paramétrica en el dominio correspondiente. Las ecuaciones paramétricas muestran que cuando$t > 0$,$x > 2$ y$y > 0$, por lo tanto, el dominio de la ecuación cartesiana debe limitarse a$x > 2$.

Para asegurar que la ecuación cartesiana sea lo más equivalente posible a la ecuación paramétrica original, tratamos de evitar el uso de funciones inversas restringidas de dominio, como las funciones trigonométricas inversas, cuando sea posible. Para ecuaciones que involucran funciones trig, a menudo tratamos de encontrar una identidad para utilizar para evitar las funciones inversas.

Ejemplo$\PageIndex{8}$

Escribir$\begin{array} {rcl} {x(t)} &= & {2\cos(t)} \\ {y(t)} &= & {3\sin(t)} \end{array}$ como una ecuación cartesiana, si es posible.

Solución

Para reescribir esto, podemos utilizar la identidad pitagórica$\cos^2(t) + \sin^2(t) = 1$.

\[x = 2\cos(t)\text{ so }\dfrac{x}{2} = \cos(t)\nonumber\]
\[y = 3\sin(t)\text{ so }\dfrac{y}{3} = \sin(t)\nonumber\]

Comenzando por la identidad pitagórica,

\[\cos^2(t) + \sin^2(t) = 1\nonumber\]Sustituir en las expresiones de la forma paramétrica
\[(\dfrac{x}{2})^2 + (\dfrac{y}{3})^2 = 1\nonumber\] Simplificar
\[\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1\nonumber\]

Esta es una ecuación cartesiana para la elipse que graficamos anteriormente.

Parametrización de Curvas

Si bien convertir de forma paramétrica a cartesiana puede ser útil, a menudo es más útil parametrizar una ecuación cartesiana, convirtiéndola en forma paramétrica.

Si la ecuación cartesiana da una variable en función de la otra, entonces la parametrización es trivial: la variable independiente en la función puede definirse simplemente como$t$.

Ejemplo$\PageIndex{9}$

Parametrizar la ecuación$x = y^3 - 2y$.

Solución

En la ecuación,$x$ se expresa como una función de$y$. Al definir$y = t$ podemos entonces sustituir eso en la ecuación cartesiana, cediendo$x = t^3 - 2t$. En conjunto, esto produce la forma paramétrica:

\[x(t) = t^3 - 2t\nonumber\]
\[y(t) = t\nonumber\]

Ejercicio$\PageIndex{3}$

Escribir$x^2 + y^2 = 3$ en forma paramétrica, si es posible.

Contestar: \[\begin{array} {rcl} {x(t)} &= & {3\cos(t)} \\ {y(t)} &= & 3\sin(t) \end{array}\nonumber\]

Además de parametrizar ecuaciones cartesianas, también podemos parametrizar comportamientos y movimientos.

Ejemplo$\PageIndex{10}$

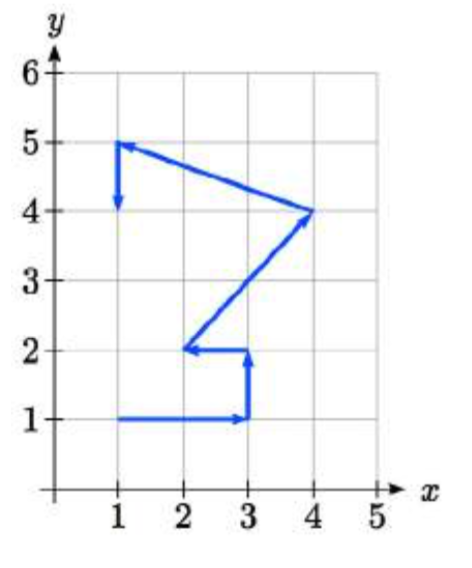
Un robot sigue el camino que se muestra. Crear una tabla de valores para las$y(t)$ funciones$x(t)$ y, asumiendo que el robot tarda un segundo en realizar cada movimiento.

$Un gráfico que muestra una secuencia de flechas lineales. Comienzan en 1 coma 1, luego apuntan secuencialmente a través de 3 coma 1, 3 coma 2, 2 coma 2, 4 coma 4, 1 coma 5, terminando en 1 coma 4.$

Solución

Ya que conocemos la dirección del movimiento, podemos introducir valores consecutivos para$t$ lo largo de la trayectoria del robot. Usando estos valores con las$y$ coordenadas$x$ y del robot, podemos crear las tablas. Por ejemplo, designamos el punto de partida, en (1, 1), como la posición en$t = 0$, el siguiente punto en (3, 1) como la posición en$t = 1$, y así sucesivamente.

$2019-07-24 9.18.55.png$

Observe cómo esto también se une a los vectores. El recorrido del robot a medida que se mueve por el plano cartesiano también podría mostrarse como vectores y se podría calcular la distancia total recorrida y el desplazamiento.

Ejemplo$\PageIndex{11}$

Se coloca una luz en el borde de una llanta de bicicleta como se muestra y la bicicleta comienza a rodar por la calle. Encuentre una ecuación paramétrica para la posición de la luz después de que la rueda haya girado en un ángulo de$\theta$.

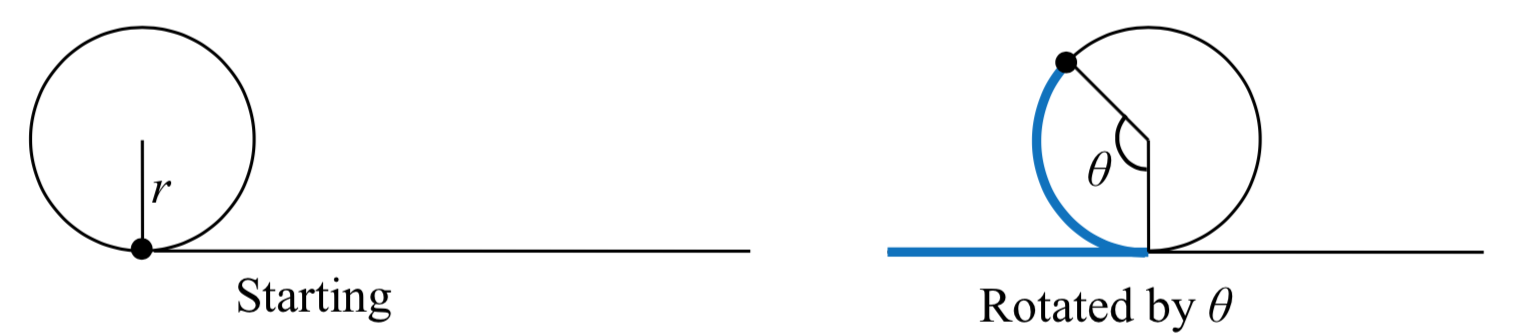
$Se muestran dos imágenes. El primero muestra un radio de círculo r sobre una línea horizontal, con un punto en la parte inferior del círculo etiquetado. El segundo cuadro está etiquetado girado por theta, y muestra el círculo movido hacia la derecha. El punto está ahora en un ángulo theta en sentido horario desde abajo. Se resalta el arco del círculo desde la parte inferior hasta el punto, y se resalta un segmento de la línea horizontal desde la izquierda hasta la parte inferior del círculo, mostrando que tienen la misma longitud.$

Solución

En relación con el centro de la rueda, la posición de la luz se puede encontrar como las coordenadas de un punto en un círculo, pero como la$x$ coordenada comienza en 0 y se mueve en dirección negativa, mientras que la$y$ coordenada comienza en el valor más bajo, las coordenadas del punto estarán dadas por:

\[x = -r\sin(\theta)\nonumber\]
\[y = -r\cos(\theta)\nonumber\]

El centro de la rueda, por su parte, se mueve horizontalmente. Permanece a una altura constante de$r$, pero la posición horizontal se moverá una distancia equivalente a la longitud del arco del círculo dibujado por el ángulo,$s = r\theta$. La posición del centro del círculo es entonces

\[x = r\theta\nonumber\]
\[y = r\nonumber\]

Combinando la posición del centro de la rueda con la posición de la luz en la rueda con relación al centro, obtenemos la siguiente ecuación paramétricaw, con$\theta$ como parámetro:

\[x = r\theta - r\sin(\theta) = r(\theta - \sin(\theta))\nonumber\]
\[y = r - r\cos(\theta) = r(1 - \cos(\theta))\nonumber\]

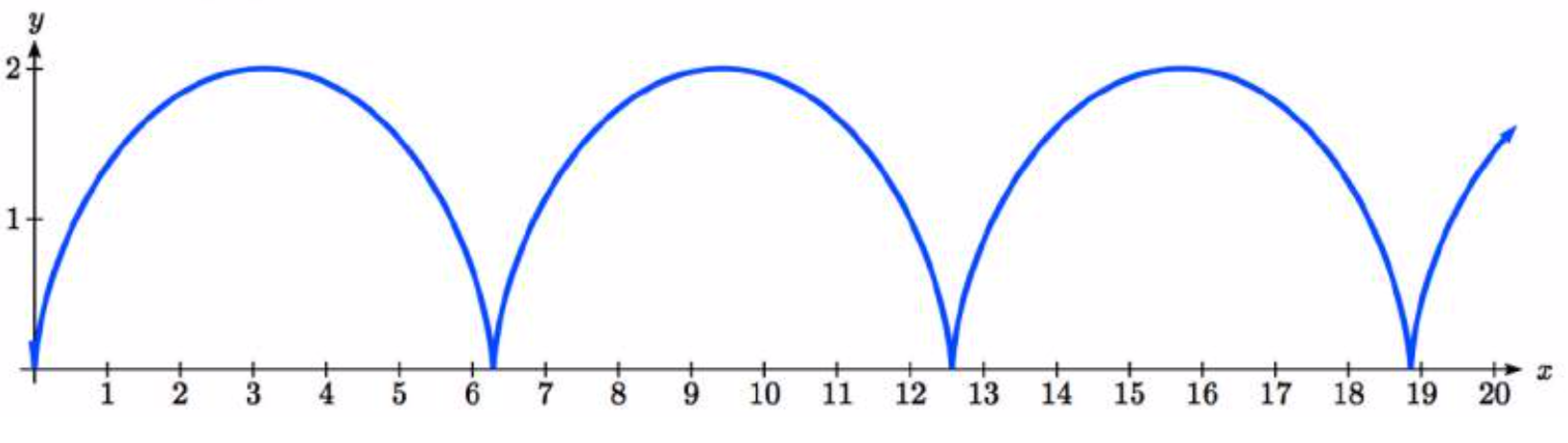
El gráfico de resultados se llama cicloide.

$Una serie de arcos repetidos. El primero comienza en el origen, se curva cóncavo hacia abajo hasta pi coma 2, luego se curva cóncavo hacia abajo a pi coma 0. Esa misma forma se repite dos veces más.$

Ejemplo$\PageIndex{12}$

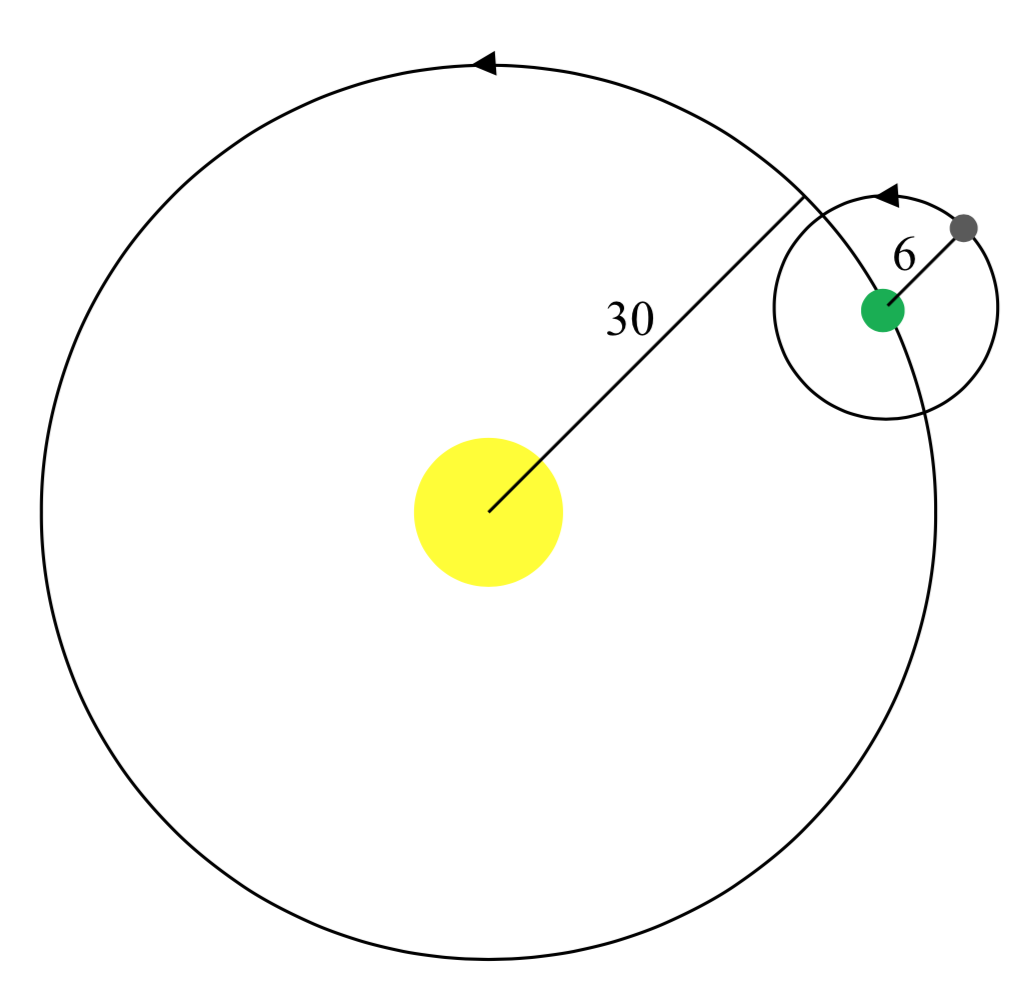
Una luna viaja alrededor de un planeta como se muestra, orbitando una vez cada 10 días. El planeta viaja alrededor de un sol como se muestra, orbitando una vez cada 100 días. Encuentra una ecuación paramétrica para la posición de la luna, relativa al centro del sol, después de$t$ días.

$Una imagen con un sol en el centro, con un radio de círculo 30 a su alrededor, con una flecha que indica movimiento en sentido antihorario. En el círculo hay un planeta, con un círculo más pequeño a su alrededor con radio 6, también con una flecha que indica movimiento en sentido antihorario. En este círculo más pequeño se muestra una luna.$

Solución

Para este ejemplo, asumiremos que las órbitas son circulares, aunque en la vida real son en realidad elípticas.

Las coordenadas de un punto en un círculo siempre se pueden escribir en la forma

\[x = r\cos(\theta)\nonumber\]
\[y = r\sin(\theta)\nonumber\]

Dado que la órbita de la luna alrededor del planeta tiene un periodo de 10 días, la ecuación para la posición de la$moon$$relative$$to$$the$$planet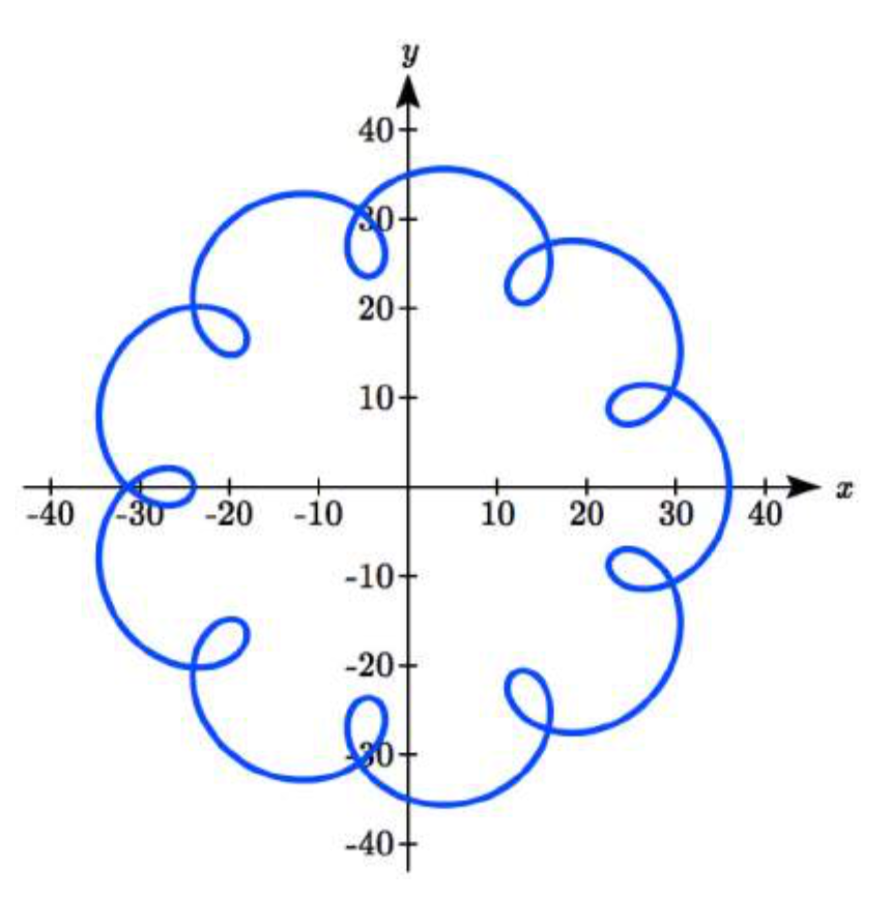$ $Un gráfico que muestra espirales más pequeñas alrededor de un círculo más grande.$ será

\[x(t) = 6\cos(\dfrac{2\pi}{10}t) = 6\cos(\dfrac{\pi}{5}t)\nonumber\]
\[y(t) = 6\sin(\dfrac{2\pi}{10}t) = 6\sin(\dfrac{\pi}{5}t)\nonumber\]

Con un periodo de 100 días, la ecuación para la posición del$planet$$relative$$to$$the$$sun$ será

\[x(t) = 30\cos(\dfrac{2\pi}{100} t) = 30 \cos (\dfrac{\pi}{50} t)\nonumber\]
\[y(t) = 30\sin(\dfrac{2\pi}{100} t) = 30 \sin (\dfrac{\pi}{50} t)\nonumber\]

Combinando estos juntos, podemos encontrar la posición del$moon$$relative$$to$$the$$sun$ como la suma de los componentes.

\[x(t) = 6\cos(\dfrac{2\pi}{5} t) = 30 \cos (\dfrac{\pi}{50} t)\nonumber\]
\[y(t) = 6\cos(\dfrac{2\pi}{5} t) = 30 \sin (\dfrac{\pi}{50} t)\nonumber\]

Aquí se muestra la gráfica resultante.

Ejercicio$\PageIndex{4}$

Una rueda de radio 4 se rueda alrededor del exterior de un círculo de radio 7. Encuentra una ecuación paramétrica para la posición de un punto en el límite de la rueda más pequeña. Esta forma se llama epicycloide.

Contestar

El centro de la rueda pequeña gira en círculo con radio 7 + 4 = 11.

Dado que la circunferencia del círculo pequeño es$8\pi$ y la circunferencia del círculo grande es$22\pi$, en el tiempo que lleva rodar alrededor del círculo grande, el círculo pequeño habrá girado$\dfrac{22\pi}{8\pi} = \dfrac{11}{4}$ rotaciones. Utilizamos esto como factor de estiramiento. La posición de un punto en el círculo pequeño será la combinación de la posición del centro de la rueda pequeña alrededor del centro de la rueda grande, y la posición del punto alrededor de la rueda pequeña:

\[x(t) = 11 \cos(t) - 4\cos(\dfrac{11}{4} t)\nonumber\]
\[y(t) = 11\sin(t) - 4\sin(\dfrac{11}{4}t)\nonumber\]

Temas Importantes de esta Sección

Ecuaciones paramétricas
Graficar$x(t)$,$y(t)$ y la$x-y$ gráfica correspondiente Croquizar gráficas y construir una tabla de valores
Convertir paramétrico a cartesiano
Convertir cartesianas a paramétricas (parametrización de curvas)