1.4: Aplicaciones

Última actualización
Guardar como PDF

Page ID: 117044

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.4 Aplicaciones
La trigonometría se utiliza a menudo para lo que se denomina “medición indirecta”. Este es un método para medir distancias inaccesibles mediante el uso de las relaciones entre longitudes y ángulos dentro de un triángulo. Dos ejemplos sencillos de este proceso son medir la altura de un árbol alto y medir la distancia a través de un cuerpo de agua. En ambos casos, si bien podría ser posible medir la distancia directamente, a menudo es mucho más fácil usar la medición indirecta.

En un ejemplo de medición indirecta, el ángulo de elevación de un objeto se puede utilizar para crear un triángulo rectángulo en el que se conocen un ángulo y un lado. Los otros lados del triángulo pueden entonces ser resueltos para. En los problemas de este texto, el ángulo de elevación normalmente se dará en el problema. Para medir realmente el ángulo de elevación de un objeto, es posible utilizar un simple transportador.

Si quisieras medir la altura de un árbol alto que se asienta sobre un terreno plano, podrías usar un transportador especialmente modificado para ello. Modificar el transportador atando un peso al extremo de una cuerda y atando el otro extremo de la cuerda a través del agujero en el transportador ayudará a medir el ángulo de elevación. Una vez que el transportador esté listo, sosténgalo boca abajo y observe la parte superior del árbol a lo largo del borde recto del transportador. El peso que cuelga hacia abajo mostrará el complemento al ángulo de elevación. En otras palabras, si el ángulo de elevación es$20^{\circ},$ la cuerda marcará una medida de$70^{\circ}$ en el transportador.

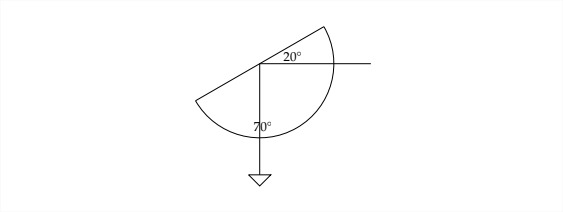
$clipboard_e13b0c9aa39c42f791e750fadf27ced45.png$

Estrechamente relacionado con el concepto del ángulo de elevación está el ángulo de depresión. Este es el ángulo que se forma al mirar hacia abajo en algo desde arriba.

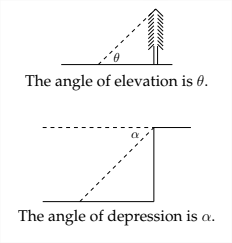
$clipboard_e06498bfd1d9482316539f4089e0412bc.png$

En una situación en la que se mide el ángulo de depresión, el ángulo de elevación y el ángulo de depresión son ángulos interiores alternos, lo que los hace iguales.

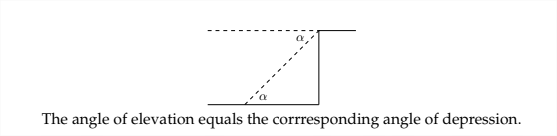
$clipboard_ea27b958c116f82e8e5ce27111e5c8a87.png$

Ejemplo 1
Paseando$100 \mathrm{ft}$ sobre un terreno plano desde la base de un árbol, un silvicultor mide el ángulo de elevación a la parte superior del árbol como$65^{\circ} .$ ¿Cuál es la altura del árbol?
La situación descrita en el problema crea un diagrama como el siguiente:
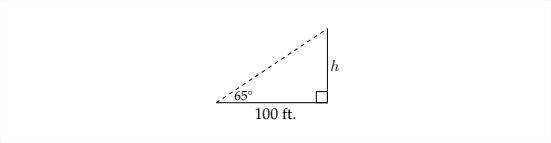
$clipboard_eef227133fd7b4c2d6401b9dc822fdce8.png$
dado que se trata de un triángulo rectángulo, podemos usar una relación trigonométrica adecuada para encontrar la altura del árbol. En este caso,
\ [ \ tan 65^ {\ circ} =\ frac {h} {100}
\] $100 * \tan 65^{\circ}=h$
$214.45 \approx h$
Entonces, el árbol mide aproximadamente 214.45 pies de altura.
Ejemplo 2
Desde la parte superior de un edificio de 125 pies de altura, el ángulo de depresión de una intersección
es$34^{\circ} .$ ¿A qué distancia de la base del edificio está la intersección?
Al igual que en el ejemplo anterior, a menudo resulta útil dibujar un diagrama.
$clipboard_e15cc6cb037d1820dc2cd7e865eb970c7.png$

Nuevamente, el ángulo de elevación será igual al ángulo de depresión correspondiente, por lo que podemos usar el triángulo como se ve a continuación para resolver el problema:
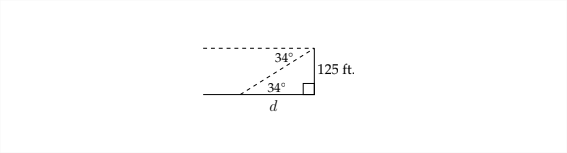
$clipboard_ee5e37044178743df9aadcfd19e7fa82f.png$
En este problema
\ [ \ tan 34^ {\ circ} =\ frac {125} {d}
\] Multiplicar en ambos lados por $d$
\ [ d *\ tan 34^ {\ circ} =125
\] Luego divide en ambos lados por$\tan 34^{\circ}$
\ [ \ begin {array} {c}
\ frac {d\ tan 34^ {\ circ}} {\ tan 34^ {\ circ}} =\ frac {125} {\ tan 34^ {\ circ}}\\
d\ approx 185.32
\ end {array}
\]

Ejemplo 3
A veces un problema involucra tanto un ángulo de elevación como un ángulo de depresión.

Desde el techo de una casa a 20 pies del suelo, el ángulo de elevación de la parte superior de un edificio de departamentos es$63^{\circ}$ y el ángulo de depresión a la base del edificio está$24^{\circ} .$ ¿Qué tan lejos de la casa está el edificio de departamentos? ¿Qué tan alto es el edificio de departamentos?

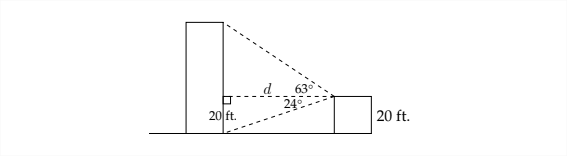
$clipboard_e6ee9f53eee59451645654fdaf6636fca.png$

Si trabajamos primero en el triángulo inferior, entonces sabemos que la altura del triángulo es$20 \mathrm{ft}$ y el ángulo opuesto a este lado es$24^{\circ} .$ Así, podemos decir que:
\ [\ begin {array} {c} \ tan 24^ {
\ circ} =\ frac {20} {d}\\
d=\ frac {20} {\ frac {20} {\ tan 24^ {\ circ}}\\
d\ approx 45\ mathrm {ft}
\ end {array}
\] Ahora que sabemos que el edificio de departamentos está a 45 pies de distancia, podemos usar el triángulo superior para determinar la altura del edificio.

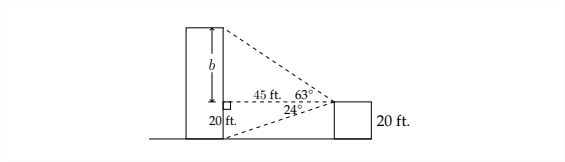
$clipboard_e3fb422c849ddcb22cdf677173370e8c5.png$

\ [ \ begin {array} {c}
\ tan 63^ {\ circ} =\ frac {b} {45}\\
45 *\ tan 63^ {\ circ} =b\\
88.3\ mathrm {ft}. \ approx b\\
20+88.3=108.3\ mathrm {ft}
\ end {array}
\] ya que la variable$b$ solo representa la parte del edificio que se encuentra en el segundo triángulo, necesitamos sumar 20 pies$b$ para encontrar la altura real del edificio.

Problemas de rumbo y dirección
Algunas aplicaciones de la trigonometría involucran la navegación de barcos. Un método común utilizado para describir la dirección en este tipo de problemas es lo que se conoce como rodamiento. El rodamiento describe una dirección por la desviación del ángulo desde el norte o el sur. Por ejemplo, la dirección que normalmente describimos como noreste es exactamente a mitad de camino entre norte y este. El rumbo hacia el noreste sería$N 45^{\circ} E$, y se lee como “Cuarenta y cinco grados al este del norte”.

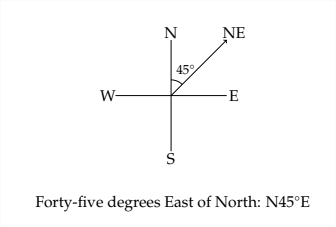
$clipboard_e64a69e0dcd5b759673704ac2da5e0ced.png$

Aquí hay algunos ejemplos de cómo se ve un rodamiento en un diagrama N-S-E-W.

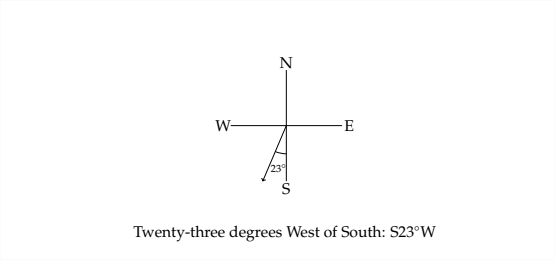
$clipboard_ee7caa1975ccdc5fb8f5a94df3023fe3b.png$

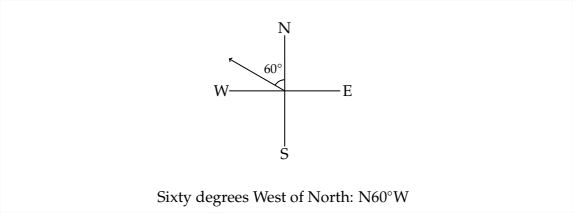
$clipboard_eba2b44a573a0337fd7d76ab16a969e6e.png$

Ejemplo 4
Santa Rosa, California, está a 7 millas al norte del parque Rohnert. Bodega Bay está a 19 millas al oeste del Parque Rohnert (mientras vuela el cuervo). ¿Cuál es el rumbo de Santa Rosa de Bodega Bay?
Primero, sería útil dibujar un diagrama para representar la situación:

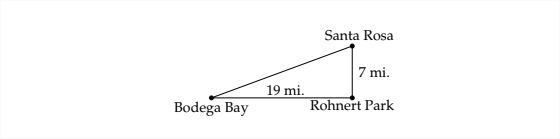
$clipboard_eeb44764ed9416885826cfb817488a521.png$

Para responder a la pregunta necesitaremos otro diagrama:

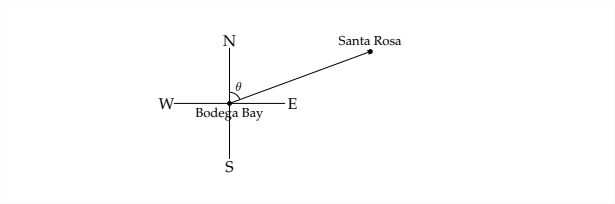
$clipboard_ec41d58665fc17d7bf1b0b32f1a0dece0.png$

Si conociéramos el ángulo$\theta$, entonces podríamos concluir que el rumbo de Santa Rosa de Bodega Bay es$\theta$ grados Este de Norte. Del diagrama anterior:
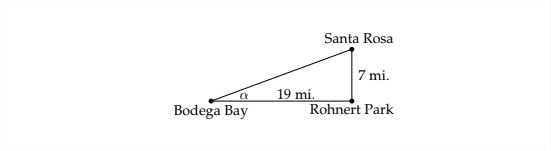
$clipboard_ebebd55c5df0dfbbc08824d491978cd6b.png$
podemos ver que no podemos encontrar$\theta$ directamente, pero podemos encontrar el complemento de$\theta$
\ [\ tan \ alpha=\ frac {7} {19}
\]\ [ $\alpha \approx 20.2^{\circ}$
\ text {Por lo tanto,}\ theta\ approx 90^ {\ circ} -20.2^ {\ circ}\ approx 69.8^ {\ circ}
\] Eso significa que el rumbo de Santa Rosa de Bodega Bay es$N 69.8^{\circ} E$, o$69.8^{\circ}$ Este
del Norte.

Ejercicios 1.4 Respuestas
redondas al$10^{t h}$
1 más cercano. Desde lo alto de un faro a 180 pies sobre el nivel del mar, el ángulo de depresión a un barco en el océano es$28^{\circ} .$ ¿Qué tan lejos está el barco de la base del faro?
2. Un helicóptero que está a 700 pies en el aire mide el ángulo de depresión a una plataforma de aterrizaje como$24^{\circ} .$ ¿A qué distancia está la plataforma de aterrizaje del punto directamente debajo de la posición actual del helicóptero?
3. Un árbol de 88 pies proyecta una sombra que mide 135 pies de largo. ¿Cuál es el ángulo de elevación del sol?
4. $\quad$Un cable de guía de 275 pies está unido a la parte superior de una torre de comunicación. Si el cable hace un ángulo$53^{\circ}$ con el suelo, ¿qué tan alta es la torre?
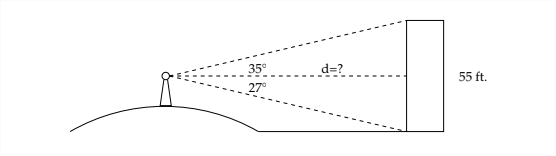
5. Una mujer parada en una colina ve un edificio que sabe que mide 55 pies de altura. El ángulo de depresión a la parte inferior del edificio es$27^{\circ}$ y el ángulo de elevación a la parte superior del edificio es$35^{\circ} .$ Encontrar la distancia en línea recta de la mujer al edificio.

$clipboard_eab9902075f71f01de6d92facf3b98859.png$

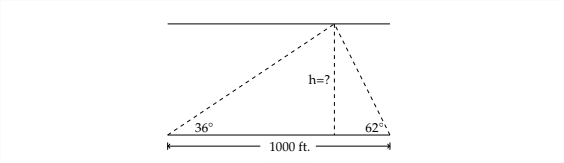
6. Para medir la altura de la nubosidad en un aeropuerto, un foco se resplandece hacia arriba en un ángulo de$62^{\circ} .$ Un observador a 1000 pies de distancia mide el ángulo de elevación al foco para ser$36^{\circ} .$ Encuentra la altura de la capa de nubes.
$clipboard_eff5f5f00f8e7d4c2803f8e250457c947.png$
7. A nivel del suelo, una torre de agua se encuentra a 430 pies de la base de un edificio. Desde uno de los pisos superiores del edificio, el ángulo de elevación hasta la parte superior de la torre de agua es$15^{\circ}$ y el ángulo de depresión hasta el fondo de la torre de agua es$28^{\circ} .$ ¿Qué altura tiene la torre de agua? ¿Qué tan alto del suelo está el observador?
8. Un avión pequeño está volando a una altitud de 7000 pies siguiendo una carretera recta directamente debajo de él. Se avisa un automóvil frente al avión con un ángulo de depresión de$72^{\circ}$ y un automóvil detrás del avión es avistado con un ángulo de depresión de$48^{\circ} .$ ¿Qué tan separados están los autos?
9. Desde un punto en el piso, el ángulo de elevación hasta la parte superior de una puerta es de 43". El ángulo de elevación al techo directamente por encima de la puerta es$56^{\circ} .$ Si el techo está a 10 pies sobre el piso, ¿qué tan alto es la puerta? ¿A qué distancia frente a la puerta se midieron los ángulos de elevación?
10. Un hombre parado en el techo de un edificio de 70 pies de altura mira el edificio de al lado. El ángulo de depresión al techo del edificio de al lado es$36^{\circ}$ El ángulo de depresión al fondo del edificio de al lado es$65^{\circ} .$ ¿Qué tan alto es el edificio de al lado?
11. Un barco sale del puerto y viaja 30 millas en dirección a$N 38^{\circ} W$ La embarcación gira$90^{\circ}$ y luego viaja en dirección$S 52^{\circ} W$ por 12 millas. En ese momento, ¿a qué distancia está el barco del puerto y cuál es el rumbo del barco desde la entrada del puerto?

12. Un hombre que camina por el desierto recorre 1.6 millas en dirección$S 57^{\circ} E .$ Luego gira$90^{\circ}$ y sigue caminando 3.2 millas en dirección En ese$N 33^{\circ} E .$ momento, ¿qué tan lejos está de su punto de partida y cuál es su rumbo desde el punto de partida?
13. Madras, Oregón, está a 26 millas al norte de Redmond. Prineville está al este de Redmond y$S 34^{\circ} 42^{\prime} E$ de Madras. ¿A cuánta distancia está Prineville de Redmond?
14. Raymond, Washington está a 22 millas al sur de Aberdeen. Montesano se debe al este de Aberdeen y$N 26^{\circ} 34^{\prime} E$ de Raymond. ¿A cuánta distancia está Montesano de Raymond?
15. Un barco viaja en un rumbo rumbo$S 41^{\circ} 40^{\prime} W$ de 84 millas. ¿Qué tan al sur y a qué distancia del oeste está el barco desde su punto de partida?
16. Un barco viaja en un rumbo$N 17^{\circ} 10^{\prime} E$ de 10 millas. ¿Qué tan al norte y a qué tan oriente está el barco desde su punto de partida?