1.3: Resolviendo triángulos

Última actualización
Guardar como PDF

Page ID: 117049

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El uso de información sobre algunos de los lados y ángulos de un triángulo para encontrar los lados y ángulos desconocidos se llama “resolver el triángulo”. Si se conocen dos lados de un triángulo, se puede utilizar el Teorema de Pitágoras para encontrar el tercer lado. Si se conoce uno de los ángulos agudos en un triángulo rectángulo, el otro ángulo será su complemento con su suma siendo$90^{\circ}$

Supongamos que tenemos un triángulo rectángulo en el que conocemos los lados, pero no ángulos. Otra situación podría implicar conocer los ángulos pero sólo un lado. ¿Cómo podríamos resolver las mediciones faltantes en estas situaciones?

Resolver problemas como estos utiliza valores precalculados de las relaciones trigonométricas para hacer coincidir las longitudes con los ángulos apropiados y viceversa. Hasta la década de 1980, estos valores se imprimieron en tablas que se incluyeron en el reverso de cada libro de texto (junto con tablas de logaritmos), pero recientemente se han programado en calculadoras utilizando métodos que se estudian en Cálculo.

La mayoría de las calculadoras tienen un botón o función diseñada para encontrar el seno inverso, el coseno inverso y la tangente inversa$\left(\sin ^{-1}, \cos ^{-1}, \text {and } \tan ^{-1}\right),$ estas son las funciones que te indican la medida del ángulo que tiene un seno, coseno o tangente igual a un valor particular.
Por ejemplo, si se nos da un ángulo$\theta$ y sabemos que el$\sin \theta=\frac{1}{2}$

$clipboard_e6bc1daa496c54bd87c1dba4aaa2e31d9.png$

Entonces podemos encontrar$\sin ^{-1}\left(\frac{1}{2}\right)$ en una calculadora, que debería devolver un valor de$30^{\circ} .$ Si la calculadora está en modo radián, devolverá un valor de$\approx 0.523598776 .$ Si dividiste este número por$\pi,$ obtendrías$0.1 \overline{6},$ lo que significa que$0.523598776 \approx \frac{\pi}{6}$ En este capítulo trabajaremos principalmente en grados. En Capítulo$2,$ cuando graficamos las funciones trigonométricas normalmente usaremos medida de radián.

Resuelve el triángulo. Redondear longitudes de lado al más cercano$100^{t h}$ y ángulos al más cercano$10^{\text {th }}$ de un grado.

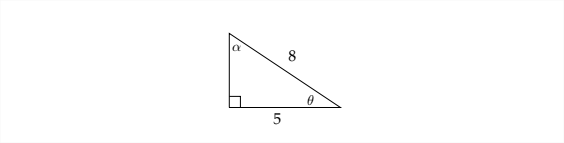
$clipboard_e20be8b37b2a288fb851325ff4294b69d.png$

Podemos encontrar el tercer lado del triángulo usando el Teorema de Pitágoras.

\ [\ begin {alineado}
a^ {2} +5^ {2} &=8^ {2}\\
a^ {2} +25 &=64
\ end {alineado}
\]$a^{2}=39$
\ [a=\ sqrt {39}\ aprox 6.24
\]

Al resolver problemas de este tipo, animo a las personas a utilizar los valores más precisos que están disponibles en el problema. De esta manera, hay menos posibilidades de que ocurra un error de redondeo.

Si tomamos los valores para los lados que se dieron en el problema (5 y 8), entonces podemos decir que

\ [\ begin {array} {c}
\ cos\ theta=\ frac {5} {8}\
\ theta=\ cos ^ {-1}\ izquierda (\ frac {5} {8}\ derecha)\
\ theta\ aproximadamente 51.3 ^ {\ circ}
\ end {array}
\]

Entonces$\alpha$ sería$90^{\circ}-51.3^{\circ}=38.7^{\circ} \approx \alpha$

Ejemplo 2
Resolver el triángulo. Redondear longitudes de lado al más cercano$100^{t h}$ y ángulos al más cercano$10^{\text {th }}$ de un grado.
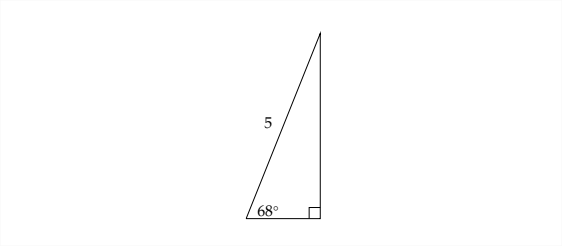
$clipboard_e856d0d6714b1762c43a9a7d0e8e981db.png$
Primero, podemos encontrar el otro ángulo en el triángulo rectángulo:$90^{\circ}-68^{\circ}=22^{\circ}$
A continuación, para encontrar los lados, elegimos una relación trigonométrica para la cual conocemos uno de los lados. En este problema, podemos usar ya sea el seno o el coseno.
$\sin 68^{\circ}=\frac{a}{5}$
Aproximación$\sin 68^{\circ}$ en una calculadora:
$0.9272 \approx \frac{a}{5}$
\ [5 * 0.9272\ aprox a
\]$4.6 \approx a$
Al aproximar un valor trigonométrico de la calculadora, es importante usar al menos 4 decimales lugares de precisión. Nuevamente, esto es para evitar errores de redondeo.
Para resolver por el lado restante podemos usar el Teorema de Pitágoras o usar el método demostrado anteriormente, pero con el$\cos 68^{\circ}$

$\cos 68^{\circ}=\frac{b}{5}$
Aproximando cos$68^{\circ}$ en una calculadora:
\ [\ begin {array} {c}
0.3746\ approx\ frac {b} {5}\\
5 * 0.3746\ approx b\\
1.9\ approx b
\ end {array}
\] Si usamos el Teorema de Pitágoras con dos lados del triángulo para encontrar el tercero, entonces diríamos que:
\ [\ begin {array} {c}
b^ {2} +4.6^ {2} =5^ {2}\\
b^ {2} +21.16=25\\
b^ {2} =3.84\\
b=\ sqrt {3.84}\ approx 1.959\ approx 2.0
\ end {array}
\] El error de redondeo en este ejemplo viene del hecho de que el primer lado que encontramos no fue exactamente$4.6 .$ Si quisiéramos una respuesta más precisa que coincida con la respuesta que encontramos usando la relación coseno, solo necesitamos más precisión en la pata del triángulo que encontramos.
El cálculo$5 * \sin 68^{\circ} \approx 4.636$ debe proporcionar suficiente precisión.
\ [\ begin {array} {c}
b^ {2} +4.636^ {2} =5^ {2}\\
b^ {2} +21.492496=25\\
b^ {2} =3.507504\
b=\ sqrt {3.507504}\ aproximadamente 1.8728\ aproximadamente 1.9
\ end {array}
\]

Ejemplo 3
Resolver el triángulo. Redondear longitudes de lado al más cercano$100^{t h}$ y ángulos al más cercano$10^{\text {th }}$ de un grado.
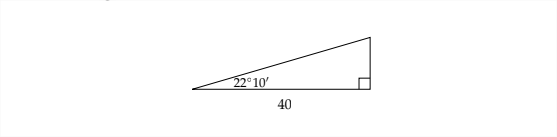
$clipboard_e062434c97f1bf6bb4c3d3b44e2997f4f.png$
Si convertimos el ángulo$22^{\circ} 10^{\prime}$ a$22.1 \overline{6}^{\circ},$ entonces el otro ángulo agudo en el triángulo rectángulo es$90^{\circ}-22.1 \overline{6}^{\circ}=67.8 \overline{3}^{\circ}$ o$67^{\circ} 50^{\prime}$
Encontrar los lados restantes requiere el uso de la función coseno o tangente.
\ [\ cos 22.1\ overrightarrow {6} ^ {\ circ} =\ frac {40} {c}
\] Aproximando cos$22.1 \overline{6}^{\circ}$ en una calculadora:
\ [0.9261\ approx\ frac {40} {c}
\] A continuación necesitamos multiplicar en ambos lados por$c:$
\ [c * 0.9261\ approx\ frac {40} {c} * c
\]$0.9261 c \approx 40$
Luego divide en ambos lados por 0.9261:
\ [\ begin {array} {c}
\ frac {0.9261 c} {0.9261}\ approx\ frac {40} {0.9261}\\
c\ approx 43.2
\ end {array}
\]

Para encontrar la otra pata del triángulo, podemos usar la relación tangente.
\ [\ tan 22.1\ overline {6} ^ {\ circ} =\ frac {a} {40}
\] Aproximando bronceado$22.1 \overline{6}^{\circ}$ en una calculadora:
\ [0.4074\ approx\ frac {a} {40}
\] Luego, multiplica en ambos lados por 40:
\ [\ begin {array} {c}
40 * 0.4074\ approx a\\
16.3\ approx a
\ end {array}
\] Podemos comprobar esta respuesta por el Teorema de Pitágoras:
\ [16.3^ {2} +40^ {2} =1865.69
\]\ [\ sqrt {1865.69}\ approx 43.2
\]

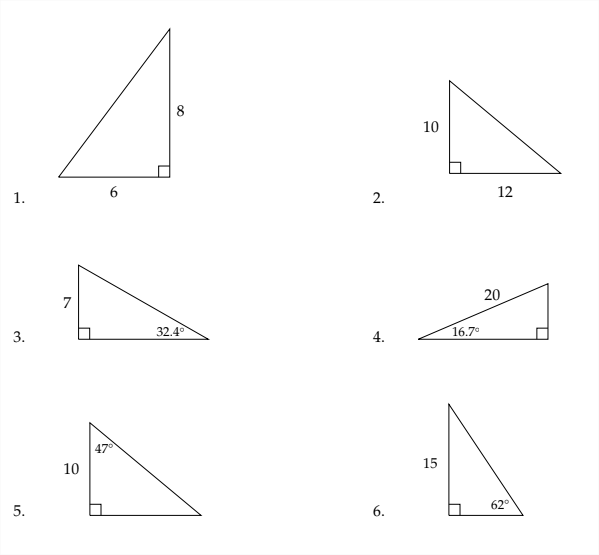
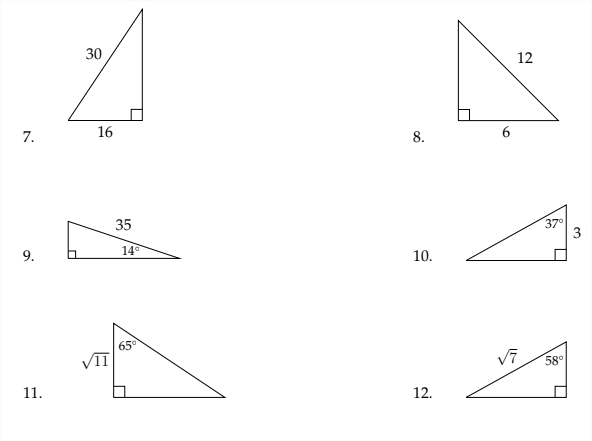
Ejercicios 1.3
En cada problema a continuación, resuelve el triángulo. Redondear longitudes de lado al más cercano$100^{t h}$ y el ángulo mide al más cercano$10^{\text {th }}$ de un grado.

$clipboard_e4f7544a73cc68dea363cd0d87830a102.png$

$clipboard_edf428a83bbdf149e8009999800551a09.png$