2.3: El desplazamiento vertical de una función trigonométrica

Última actualización
Guardar como PDF

Page ID: 117039

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

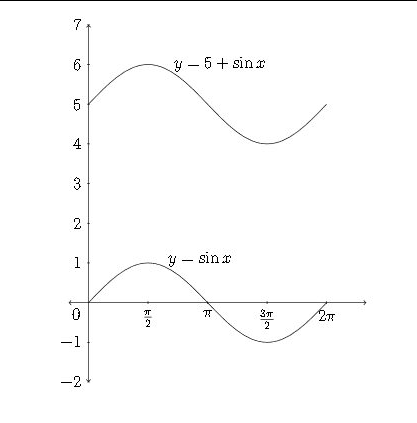
Si se suma o resta una constante a una función trigonométrica, esto afectará a los$y$ -valores de la función Si consideramos la función$y-5+\sin x,$ entonces cada uno de los$y$ valores estándar tendría 5 agregados a if, lo que desplazaría la gráfica hacia arriba 5 unidades.
El siguiente gráfico considera solo los valores cuadránticos para la función sinusoidal:
\ begin {tabular} {|c|c|c|}
\ hline$\theta$ &$\sin \theta$ &$5+\sin \theta$\\
\ hline 0 & 0 & 5\\
\ hline$\pi / 2$ & 1 & 6\\ hline
\ hline$\pi$ & 0 & 5\\
\ hline$3 \pi / 2$ & -1 & 4\\
\ hline$2 \pi$ & 0 & 5\\
\ hline
\ end {tabular}

$clipboard_ede5c070d07c8fe55cf1bb0789cfb4041.png$

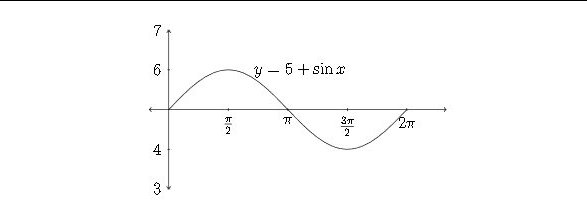
A veces el$x$ eje -se dibuja a través de la línea que es el nuevo “cero” o “línea media” para la función - en este caso sería$y-5$

$clipboard_e87e20b7638d21dc26d41fc558583cbb8.png$

Al igual que, una constante negativa movería el gráfico hacia abajo, ya que cada valor y sería menor que el$y$ valor -correspondiente en la función sinusoidal estándar

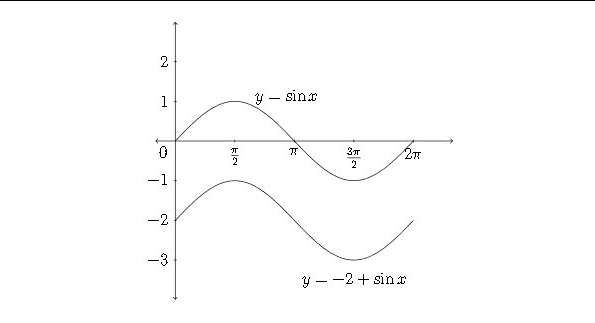
$clipboard_eaa9d8adfd3a3e651563da20ddf802696.png$

En los ejemplos anteriores la constante se ha escrito frente a la función sinusoidal para mayor claridad. A menudo la constante se escribe después de la función:
\ [\ begin {array} {c}
y-\ sin x+5\
\\ mathrm {or}\\
y-\ sin x-2
\ end {array}
\]

Ahora hemos examinado tres de las cuatro transformaciones de funciones trigonométricas que se discuten en este capítulo: amplitud, periodo y desplazamiento vertical. Una ecuación general para una sinusoide que involucra estas tres transformaciones sería:
\ [ Y=A\ sin (B x) +D
\] O
\ [ y=A\ cos (B x) +D
\] Al determinar una ecuación a partir de una gráfica que implica un desplazamiento vertical, el valor de$A$ will ser la mitad de la distancia entre los valores máximo y mínimo:
\ [ A=\ frac {m a x-m i n} {2}
\] y el valor de$D$ será el promedio de los valores máximo y mínimo:
\ [ D=\ frac {m a x+m i n} {2}
\]

Ejemplo
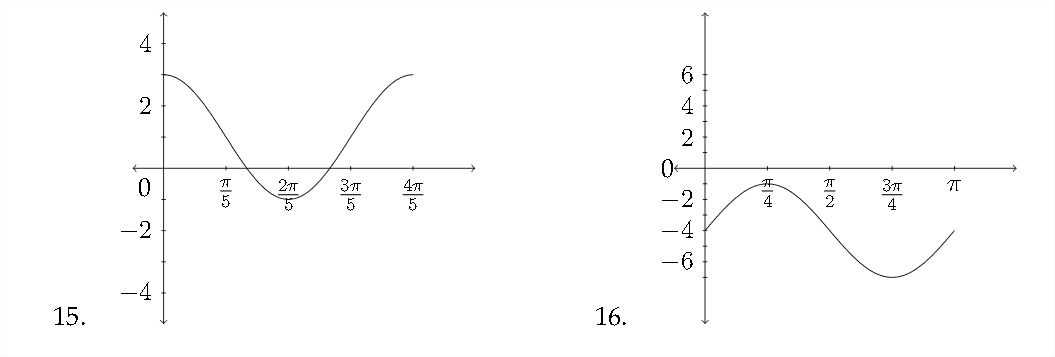
Determinar una ecuación que satisfaga la gráfica dada.

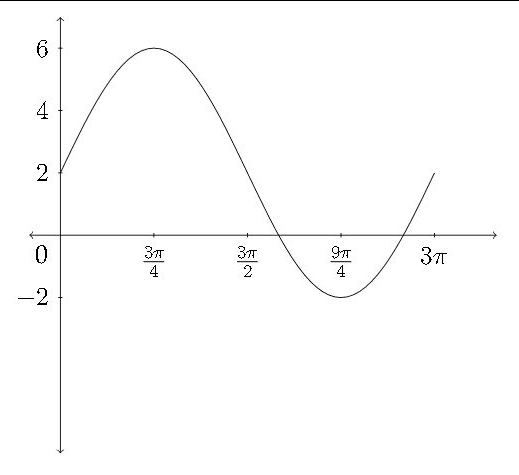
$clipboard_eb9a5a41b697448191e95f61ae0e448b2.png$

En esta gráfica, el$y$ valor máximo es 6 y el$y$ valor mínimo es$-2 .$ El promedio de estos dos:
\ [ \ frac {m a x+m i n} {2} =\ frac {6+ (-2)} {2} =\ frac {4} {2} =2=D
\] es el valor del$D,$ desplazamiento vertical.
La distancia entre 6 y -2 es la$6-(-2)=8 .$ mitad de la distancia entre el$\max$ y$\min$ es$4,$ que es el valor de$A$
\ [\ frac {m a x-m i n} {2} =\ frac {6- (-2)} {2} =\ frac {8} {2} =4=A
\]

La gráfica completa un ciclo completo entre 0 y$3 \pi,$ así el periodo sería$3 \pi$ y el valor de$B$ sería$B=\frac{2 \pi}{P}=\frac{2 \pi}{3 \pi}=\frac{2}{3}=B .$ Así que una ecuación correcta para la gráfica sería:
\ [ y=4\ sin\ frac {2} {3} x+2
\]

Ejercicios 2.3
Determinar la Amplitud, Período y Desplazamiento Vertical para cada función a continuación y graficar un periodo de la función. Identificar los puntos importantes en los$y$ ejes$x$ y.
1. $\quad y=\sin x+1$
2. $\quad y=\cos x-1$
3. $\quad y=2 \cos x-\frac{1}{2}$
4. $\quad y=5 \sin x+4$
5. $\quad y=-\sin \left(\frac{1}{4} x\right)+1$
6. $\quad y=-\cos (2 x)+7$
7. $\quad y=\frac{1}{3} \sin (\pi x)-4$
8. $\quad y=-\frac{1}{2} \cos (2 \pi x)+2$
9. $\quad y=5 \cos \left(\frac{1}{2} x\right)+1$
$10 . \quad y=4 \sin \left(\frac{1}{3} x\right)-1$
11. $\quad y=3 \cos x+2$
12. $\quad y=2 \sin x+3$
13. $\quad y=2-4 \cos (3 x)$
14. $\quad y=5-3 \sin (2 x)$

Determinar una ecuación que satisfaga la gráfica dada.

$clipboard_ef06827032e823eb3136b6c1ebd4b1738.png$

$clipboard_e43a8453a2e534595bf2ec5bd31d3044e.png$