4.4: Aplicaciones

Última actualización
Guardar como PDF

Page ID: 117062

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En las secciones anteriores sobre aplicaciones, vimos situaciones en las que se utilizó la trigonometría de triángulo rectángulo para encontrar distancias y ángulos. En esta sección, utilizaremos la Ley de los senos y la Ley de los cosenos para encontrar distancias y ángulos.

Ejemplo$\PageIndex{1}$

Un automóvil viaja por una carretera recta, en dirección oeste durante 1 hora, para luego viajar por otra carretera recta al noroeste durante media hora. Si la velocidad del auto era constante de 50 mph ¿a qué distancia está el auto de su punto de partida?

Solución

Primero, dibujemos un diagrama:

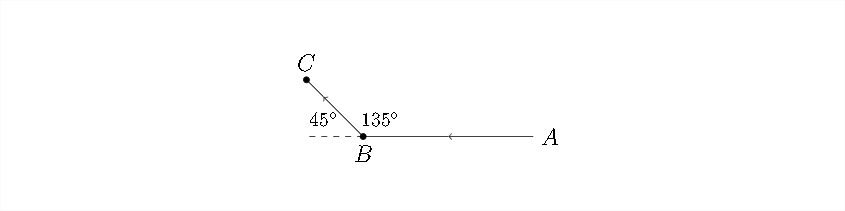
$clipboard_eefb87e096135b608e3c071bb2b6a2d34.png$

En la imagen de arriba, conocemos los ángulos$45^{\circ}$ y$135^{\circ}$ por la dirección en que viajaba el automóvil. La dirección noroeste corta exactamente a mitad de camino entre norte y oeste creando un$45^{\circ}$ ángulo. En el otro lado de este$45^{\circ}$ ángulo hay un$135^{\circ}$ ángulo que está en el triángulo que usaremos para responder a la pregunta (triángulo$A B C$).

La longitud de$\overline{A B}$ es de 50 millas y la longitud de$\overline{B C}$ es de 25 millas. Esto proviene de la información sobre la velocidad y el tiempo de viaje dada en el problema. Entonces el triángulo que necesitamos para responder a la pregunta se muestra a continuación:

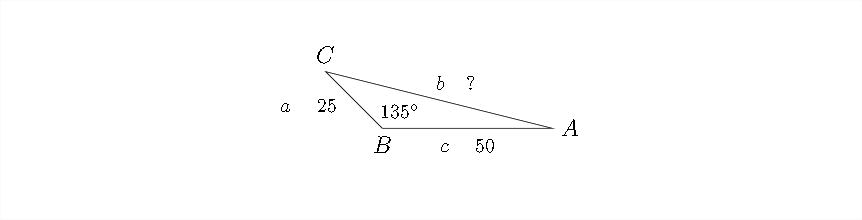
$clipboard_e23d81ccb6e827cadc4d35bf2c19d0a84.png$

Podemos usar la Ley de cosenos para resolver este problema:
\ [ \ begin {array} {c}
b^ {2} =a^ {2} +c^ {2} -2 a c\ cos B\\
b^ {2} =25^ {2} +50^ {2} -2 * 25 * 50 *\ cos 135^ {\ circ}\\
b^ {2}\ approx 625+25+2500-2500 * (-0.7071)\\
b^ {2}\ aprox 3125+1767.75\\
b^ {2}\ approx 4892.75\\
b\ approx 69.9\ mathrm {millas}
\ end {array}
\]

Ejemplo$\PageIndex{2}$

Un piloto vuela un avión en camino recto durante 2.5 horas y luego hace una corrección de rumbo, dirigiéndose$10^{\circ}$ a la izquierda del rumbo original. El piloto vuela entonces en esta dirección durante 1 hora. Si la velocidad del avión es una constante$350 \mathrm{mph}$, ¿a qué distancia está el avión de su posición inicial?

Solución

Nuevamente, comenzaremos por hacer un diagrama:

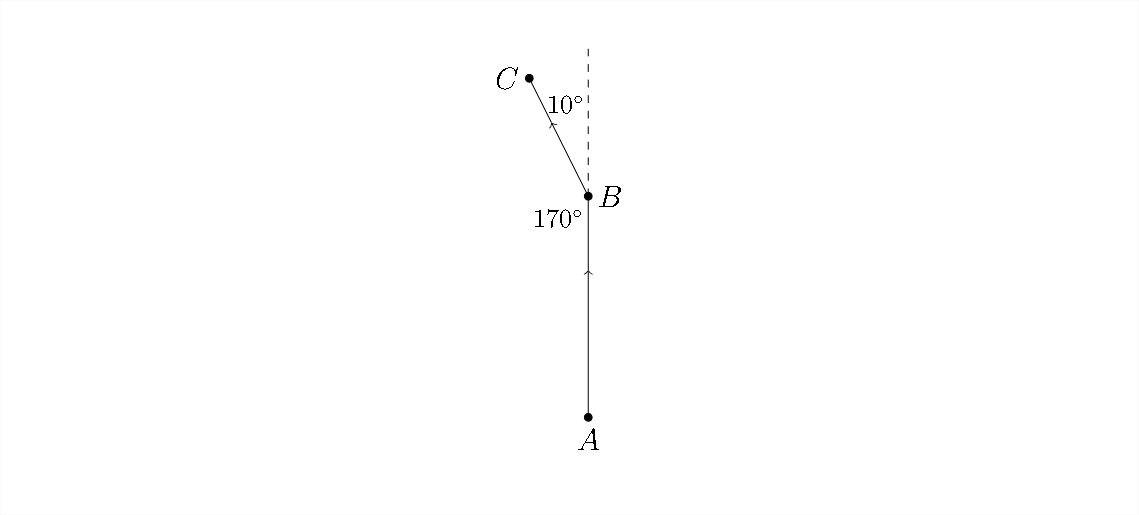
$clipboard_eb3040ee063bcae03ab1ab4b0fd57b530.png$

En este problema, estaremos trabajando con triángulo$A B C$, que se muestra a continuación. Podemos calcular las longitudes de$\overline{A B}$ y$\overline{B C}$ a partir de la información dada en el problema y usarla para calcular la longitud de$\overline{A C}$:

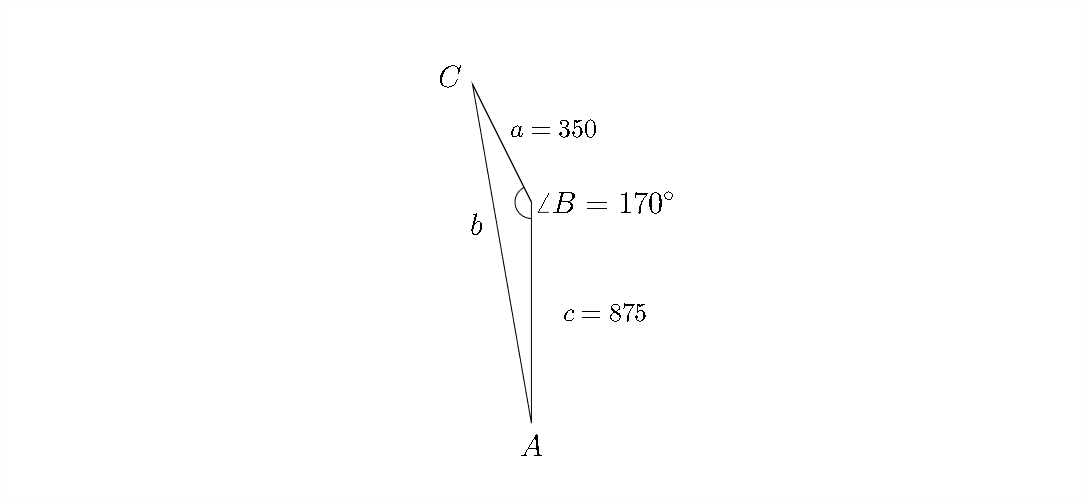
$clipboard_e14b6edb5c6ea673728038bdd527053b0.png$

Usando la Ley de cosenos:
\ [ \ begin {array} {c}
b^ {2} =a^ {2} +c^ {2} -2 a c\ cos B\\
b^ {2} =350^ {2} +875^ {2} -2 * 350 * 1050 *\ cos 170^ {\ circ}\\
b^ {2}\ approx 122.500+765.625-735,000 * (-0.9848)\\
b^ {2}\ aprox 888,125+723,828\\
b^ {2}\ aprox 1.611.953\\
b\ aprox 1270\ mathrm {millas}
\ end {array}
\]

Ejemplo$\PageIndex{3}$

Un piloto sale del aeropuerto en Bend, se dirige hacia Corvallis con el rumbo$N 70^{\circ} W .$ Recorre las 103 millas y hace una entrega antes de despegar y volar en rumbo de 72 millas$N 25^{\circ} E$ para llegar a Portland.

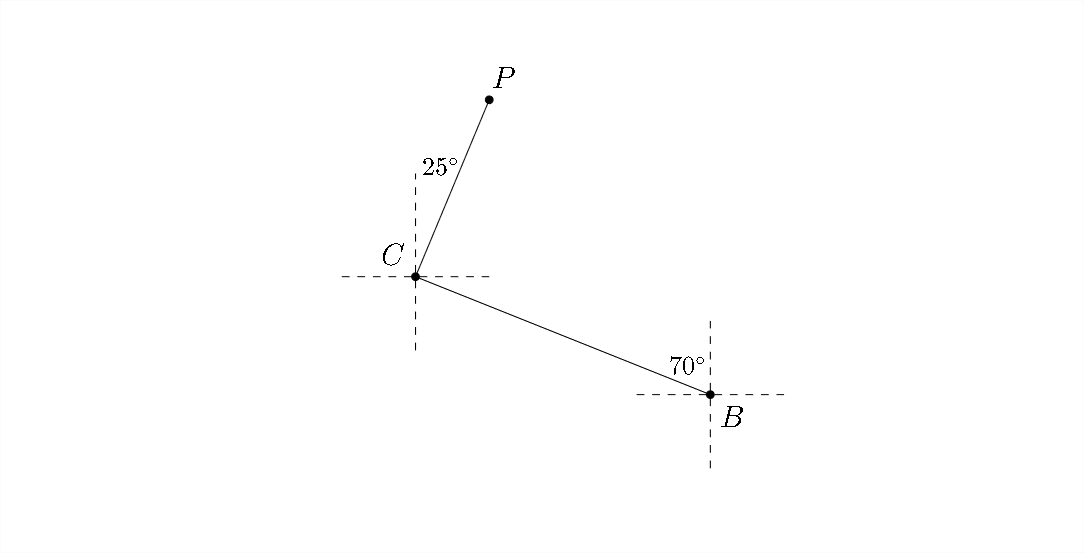
$clipboard_e4a878b214c3780120c6cc84548bb086d.png$

a) Con base en esta información, encuentre la distancia aérea entre Portland y Bend.
b) Encontrar el rumbo de Portland a Bend.

Solución

En este problema, se ha dado un diagrama. Vamos a enmendar esto para convertirlo en un triángulo:

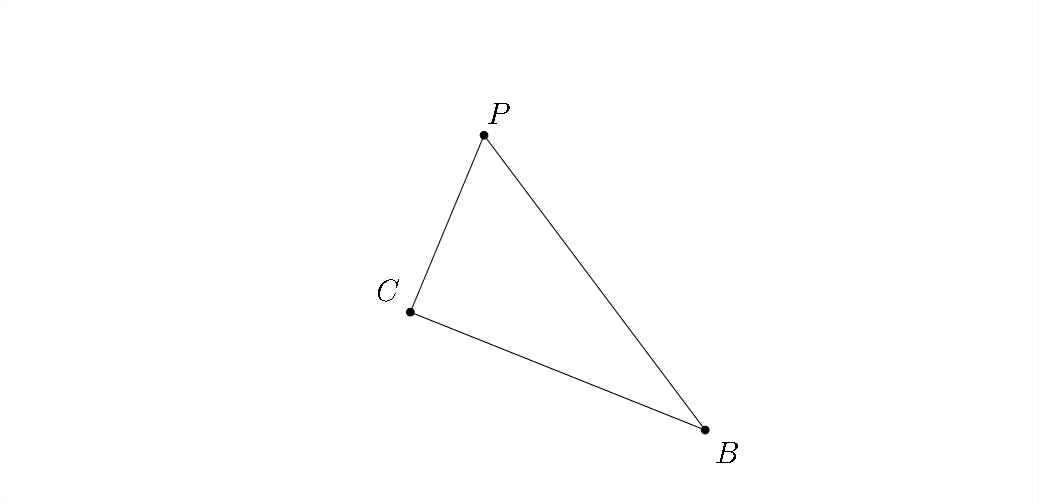
$clipboard_e6e922fa6811a503062ed12271bdfea17.png$

Llenar las medidas de los ángulos es complicado en este problema, así que volvamos a ver el diagrama original:

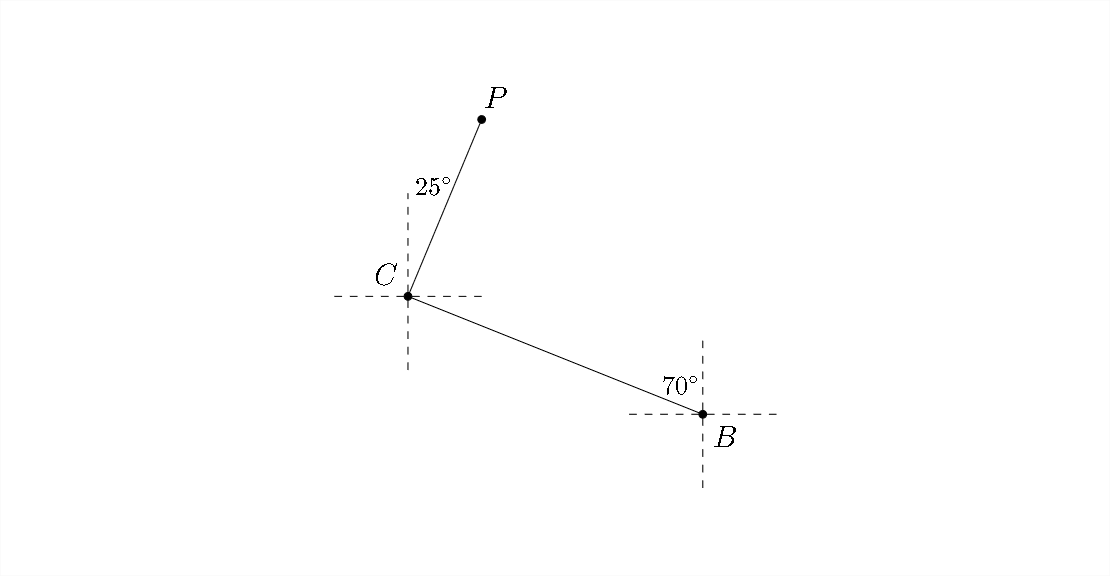
$clipboard_e9b6e88aef01d33bedd9a60709e3a0d8c.png$

Si extendemos la línea discontinua hacia el este desde Corvallis para que se encuentre con la línea discontinua que
corre hacia el norte desde Bend, podemos crear un triángulo que nos muestre que el ángulo$\angle B C X=20^{\circ} .$ Además, observe que$\angle P C X=\left(90^{\circ}-25^{\circ}\right)=65^{\circ}$

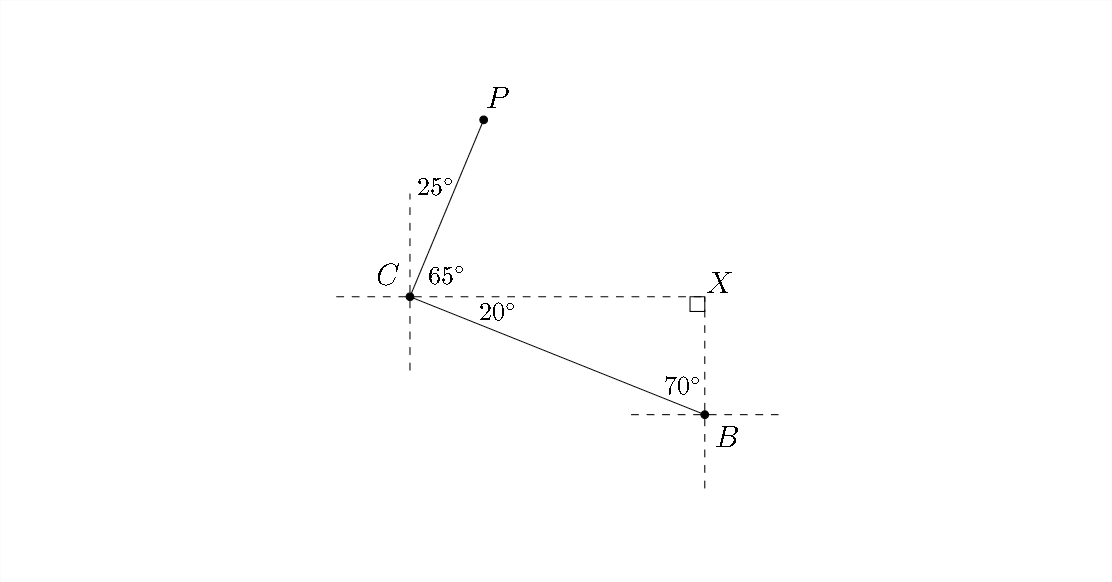
$clipboard_e569c96fb8116fd223f7cc19a426d3bb8.png$

Esto significa que$\angle B C P=85^{\circ} .$ Sabemos por el problema que$\overline{B C}=103$ y$\overline{C P}=72 .$ vamos a necesitar encontrar la longitud$\overline{B P}$ y la medida de$\angle C P B$ para responder a las preguntas.

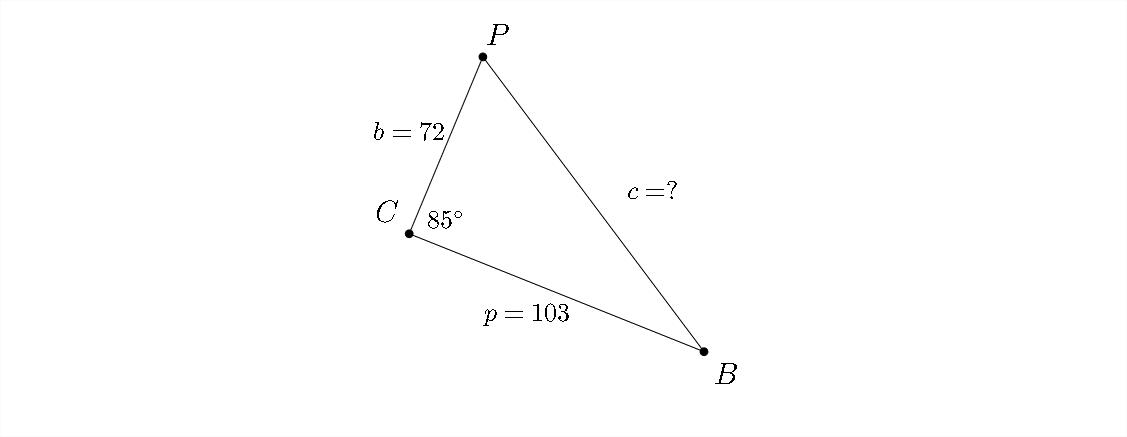
$clipboard_eab31d43d501c6ebe9f0d67cb71091a78.png$

Ahora estamos trabajando con un triángulo como el que se muestra arriba, así podemos usar la Ley de los cosenos para encontrar la distancia aérea de Portland a Bend:
\ [ \ begin {array} {c}
c^ {2} =b^ {2} +p^ {2} -2 b p\ cos C\\
c^ {2} =72^ {2} +103^ {2} -2 * 72 * 103 * cos\ 85^ {\ circ}\\
c^ {2}\ aprox 5184+10.609-14,832 * (0.087156)\\
c^ {2}\ aprox 15.793-1292.7\\
c^ {2}\ aproximadamente 14.500.3\\
c\ aprox 120.4\ texto {millas}
\ end {array}
\]

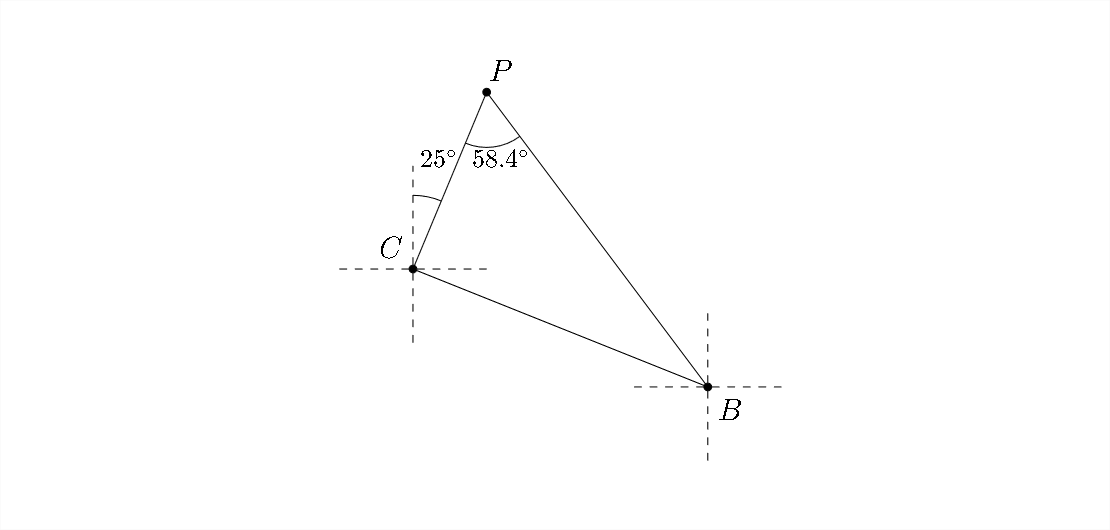
Para encontrar$\angle P,$ usaremos la Ley de los senos:

\ [ \ begin {array} {c}
\ frac {\ sin 85^ {\ circ}} {120.4} =\ frac {\ sin P} {103}\\
103 *\ frac {\ sin 85^ {\ circ}} {120.4} =\ sin P\\
103 *\ frac {0.9962} {120.4}\ approx\ sin P\\
0.85223 aprox\\ sin P\\
58.4^ {\ circ}\ aproximadamente P
\ final { matriz}
\]

Ahora que conocemos la medida de$\angle P$, podemos determinar el rumbo de Bend de Portland.

$clipboard_e777a83a38543c68c154a08913e7cbcf1.png$

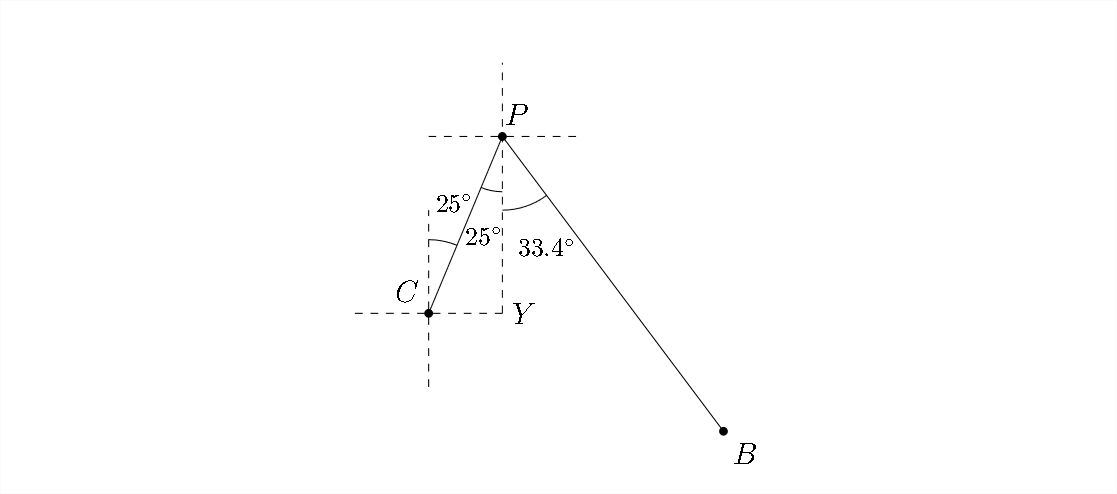
En la imagen de abajo note que$\angle Y P C=25^{\circ} .$ Esto significa que el rumbo de Portland a Bend será al este de sur por la diferencia entre$\angle P=58.4^{\circ}$ y$\angle Y P C=25^{\circ} .$ Esto hace que el rumbo de Bend de Portland sea igual a$S 33.4^{\circ} E$

$clipboard_e607ed957471b3a2dd652310cadb22643.png$

Ejemplo$\PageIndex{4}$

Una torre de 125 pies se encuentra en la ladera de una montaña que está inclinada$32^{\circ}$ a la horizontal. Un cable de sujeción debe ser unido a la parte superior de la torre y anclado en un punto a 55 pies cuesta abajo desde la base de la torre. Encuentre la longitud más corta de cable necesaria.

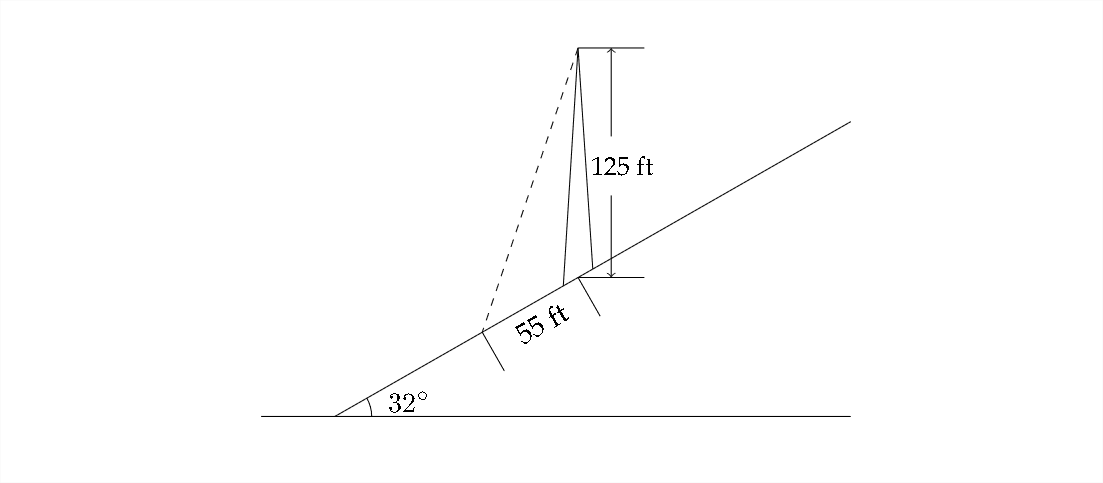
$clipboard_e97e32ee9b35fc1468ea09c5dc18bf322.png$

Solución

Un aspecto importante en la solución de este problema es identificar un triángulo en el problema que involucra la cantidad desconocida que se nos pide encontrar. Si estamos buscando la longitud del cable de sujeción, podemos usar un triángulo que involucre el cable, la distancia desde el cable hasta el centro de la torre y la altura de la torre:

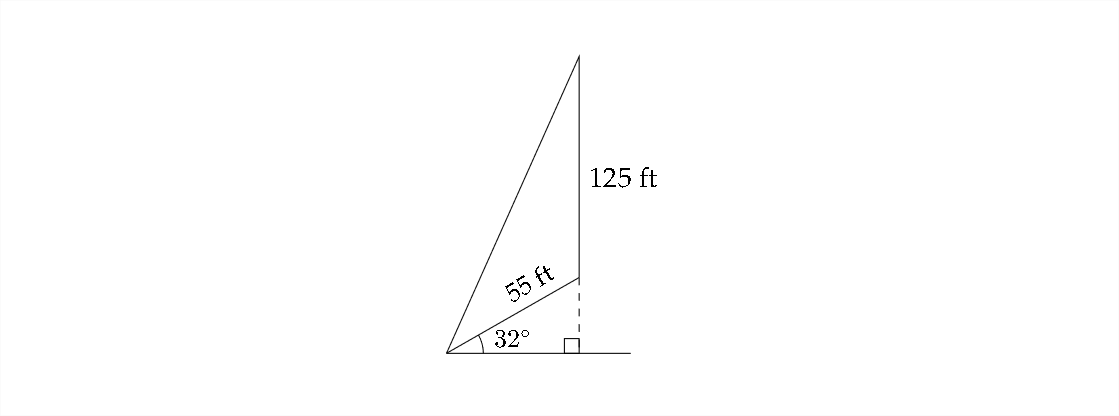
$clipboard_e8437a8310f0fb2d91f4cccc48cbeda34.png$

El ángulo entre la horizontal y el cerro se mantendrá$32^{\circ}$ en cualquier punto del cerro. Si dejamos caer una perpendicular a la horizontal, podremos encontrar el ángulo incluido entre los dos lados dados.

En el pequeño triángulo rectángulo, conocemos el ángulo de 32'. Eso significa que el otro ángulo agudo debe ser$58^{\circ}$, y el ángulo suplementario (que está en el triángulo que nos interesa$)$ será$122^{\circ}$

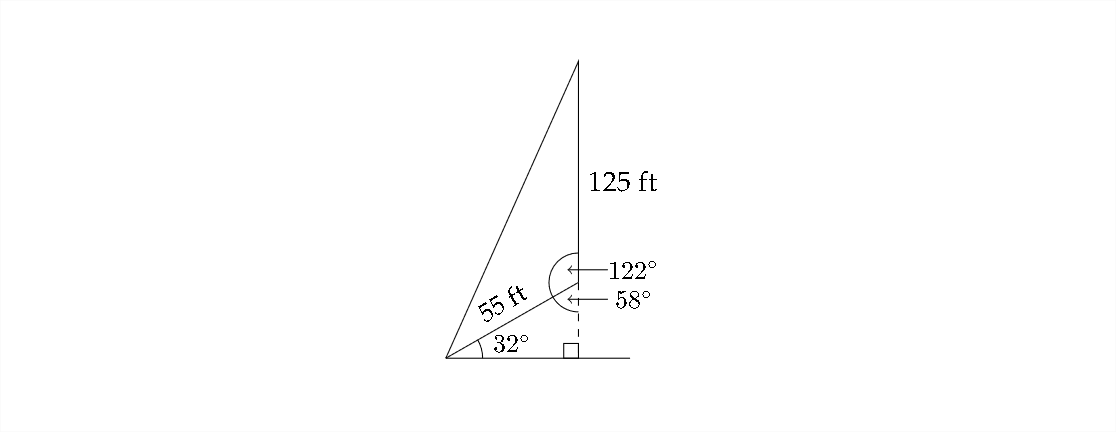
$clipboard_e8934372938e8799c812483c131ae43e9.png$

Ahora podemos usar la Ley de cosenos para encontrar la longitud del cable de sujeción:

\ [ \ begin {array} {c}
x^ {2} =125^ {2} +55^ {2} -2 * 125 * 55 *\ cos 122^ {\ circ}\\
x^ {2} =15,625+3025-13.750 *\ cos 122^ {\ circ}\
x^ {2}\ aprox 18,650+7286.39\
x^ {2}\ aprox 25,936.39\\
x\ aprox 161\ texto {pies}
\ final { matriz}
\]

Ejercicios

1. Dos caminos rectos divergen en un ángulo de$50^{\circ}$. Dos autos salen de la intersección en$1 \mathrm{pm},$ uno viajando$60 \mathrm{mph}$ y el otro viajando$45 \mathrm{mph}$. A qué distancia están los autos (como vuela el cuervo) a las$1: 30 \mathrm{pm} ?$
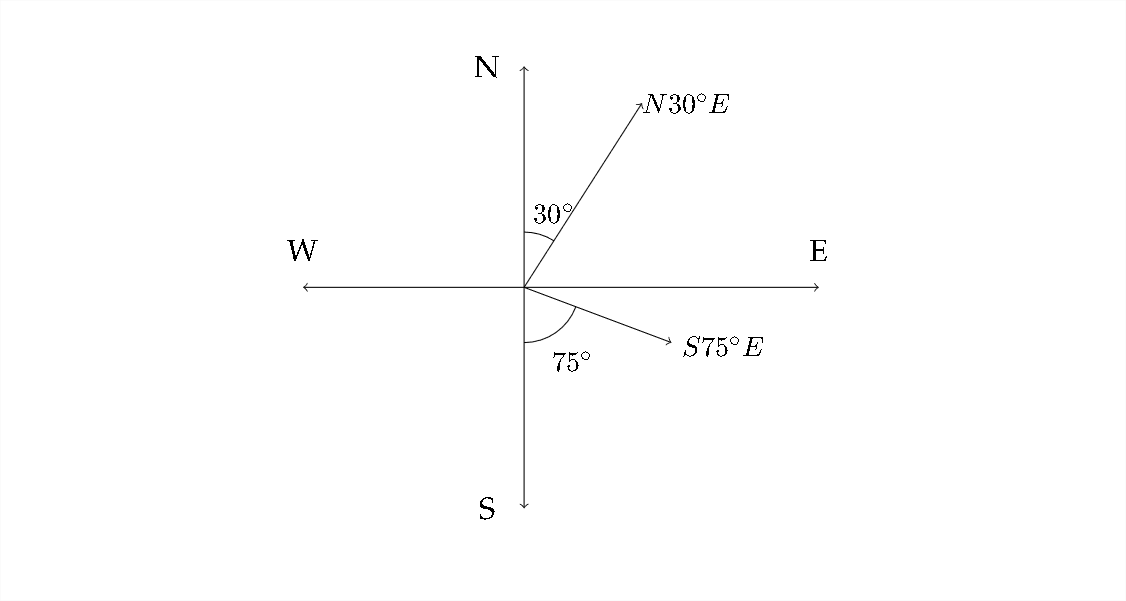
2. Dos embarcaciones salen del mismo puerto al mismo tiempo. Uno viaja a una velocidad de
$40 \mathrm{mph}$ en dirección$N 30^{\circ} E$ y el otro viaja a una velocidad de 28 mph en dirección$S 75^{\circ} E .$ ¿A qué distancia están las dos embarcaciones después de una hora?

$clipboard_e53b75464208953795c61b2bb994cc5dd.png$

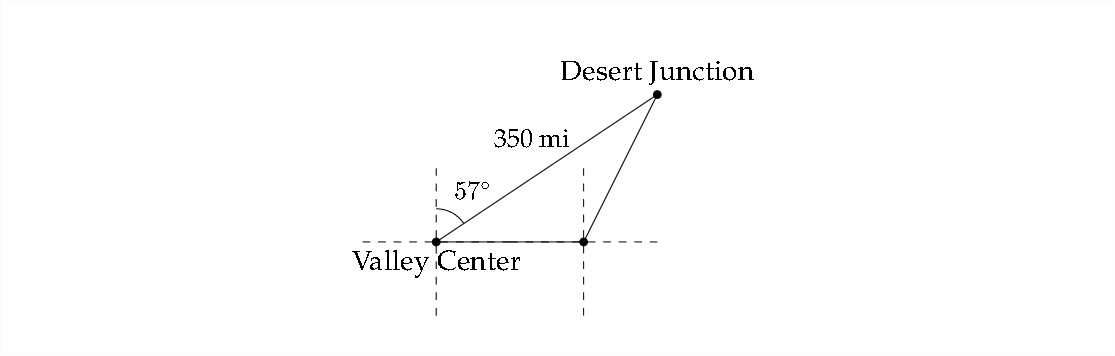
3. El aeropuerto en Desert Junction está a 350 millas del aeropuerto en Valley Center al rumbo de$N 57^{\circ} E .$ Un piloto que quiere volar desde Valley Center a Desert Junction vuela erróneamente hacia el este a 225 mph durante 30 minutos antes de corregir el error. ¿A qué distancia está el avión de su destino cuando el piloto nota el error? ¿Qué rumbo debe usar el avión para llegar a Desert Junction?

$clipboard_e10c97479a12e866e23875c61c0feb03f.png$

4. Un avión sale del aeropuerto$A$ y viaja 520 millas al aeropuerto$B$ en una dirección de$N 35^{\circ} W .$ El avión sale del aeropuerto$B$ y viaja al aeropuerto$C 310$ millas de distancia en un rumbo de$S 65^{\circ} W$ desde aeropuerto$B .$ Encuentra la distancia de aeropuerto$A$ a aeropuerto$C .$

5. Dos aviones despegan al mismo tiempo de un aeropuerto. El primer avión vuela a 300 mph a una dirección de$S 45^{\circ} E .$ El segundo avión vuela a una dirección de$S 5^{\circ} W$ con una velocidad de 330 mph. ¿Qué tan lejos están después de las 3 horas?

6. Dos aviones salen de un aeropuerto al mismo tiempo. Sus velocidades son$180 \mathrm{mph}$ y$110 \mathrm{mph},$ y el ángulo entre sus trayectorias de vuelo es$43^{\circ} .$ ¿Qué tan lejos están después de 2.5 horas?

7. Dos barcos dejan una entrada portuaria al mismo tiempo. El primero viaja a una velocidad de 23 mph y el segundo viaja a 17 mph. Si el ángulo entre los cursos de los barcos es$110^{\circ},$ ¿a qué distancia están después de una hora?

8. Un barco sale de la entrada a un puerto y viaja 15 millas con un oso$\operatorname{ing} S 10^{\circ} W,$ luego gira y recorre 45 millas con un rumbo de$N 43^{\circ} W .$ ¿Qué tan lejos de la entrada del puerto está el barco y cuál es el rumbo del barco desde el puerto?

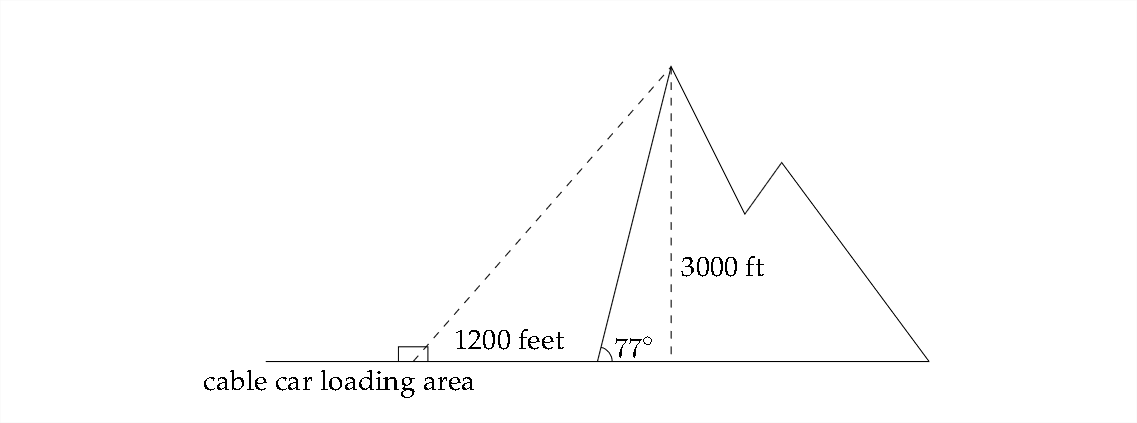
9. Una montaña empinada se inclina$77^{\circ}$ a la horizontal y se eleva 3000 pies sobre la llanura circundante. Se va a instalar un teleférico que conectará la llanura con la cima de la montaña. La distancia desde el pie de la montaña hasta el área de carga de entrada del teleférico es de 1200 pies (ver diagrama a continuación). Encuentre la longitud más corta necesaria del cable.

$clipboard_e1b5fe1f971897b6e9969db67ed7b6a51.png$

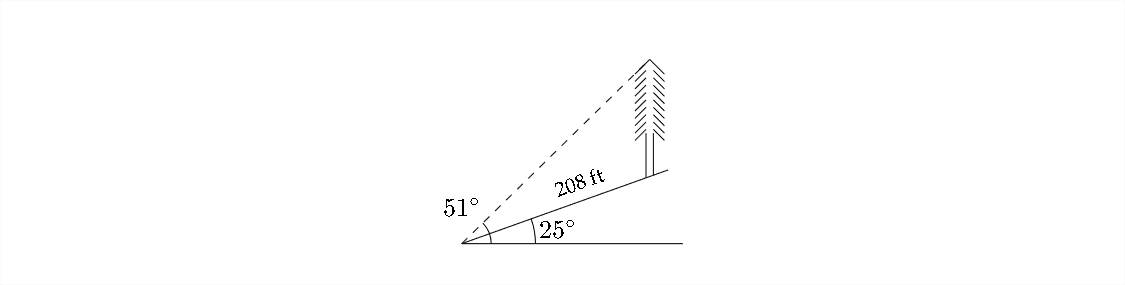
10. Un árbol en una ladera proyecta una sombra cuesta$208 \mathrm{ft}$ abajo de la colina. Si el ángulo de inclinación de la ladera es$25^{\circ}$ con respecto a la horizontal y el ángulo de elevación del$\operatorname{sun}$ es$51^{\circ},$ encontrar la altura del árbol.

$clipboard_ebf5e859d1e63cb61dcd8ce59a859afee.png$