4.3: La Ley de los Cosinos

Última actualización
Guardar como PDF

Page ID: 117066

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hay situaciones en las que la Ley de los senos no puede ser utilizada para resolver un triángulo. En el diagrama a continuación, tenemos información sobre dos lados y el ángulo incluido:

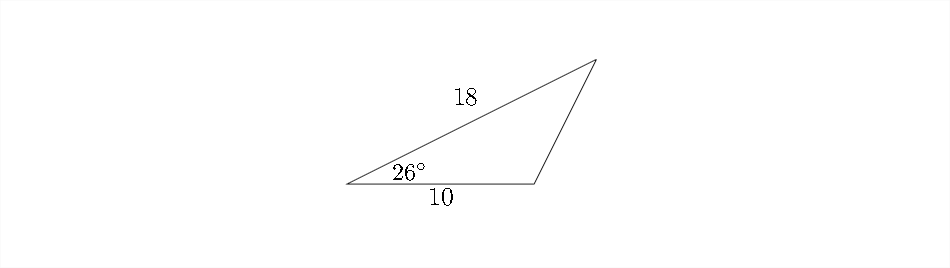
$clipboard_e1d444f5ea3d12a19d0551c2f0ce8013d.png$

El problema anterior carece de un par completo ángulo-lado el cual es necesario para establecer el cálculo de la Ley de los senos.

Otra situación común involucra un triángulo en el que se conocen los tres lados pero no se conocen ángulos:

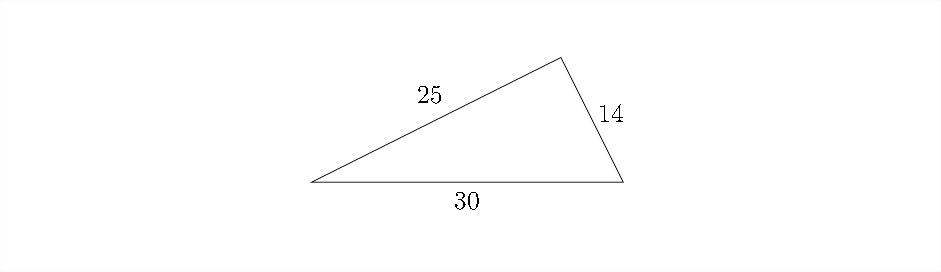
$clipboard_e6a1e6575fd4c99a23667c6b0fe5506df.png$

Nuevamente, la falta de un par ángulo-lado nos impediría establecer un cálculo de Ley de senos.

La Ley de Cosinos es una forma de sortear esta dificultad. Usar la Ley de los cosenos es más complicado que usar la Ley de los senos, sin embargo, como acabamos de ver, la Ley de los senos no siempre será suficiente para resolver un triángulo.

Para derivar La Ley de los cosenos, comenzamos con un triángulo arbitrario, como el que se ve en la página siguiente:

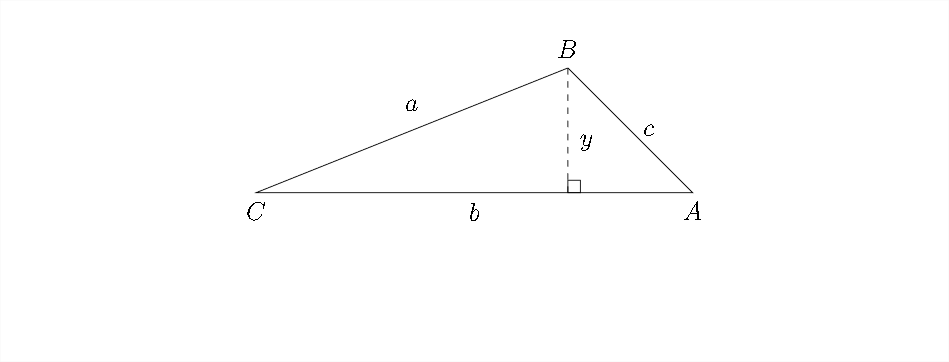
$clipboard_e767303295b4f98ae3eaea9b57e77fd92.png$

En este diagrama hemos tomado el triángulo arbitrario y creado una perpendicular con longitud$y .$ A partir de esto, podemos decir eso$\sin C=\frac{y}{a}$ y eso$a \sin C=y$

Podemos dividir el lado$A C$ en dos pedazos$A D$ y$C D,$ como se ve abajo, y etiquetar la distancia$C D$ como$x$

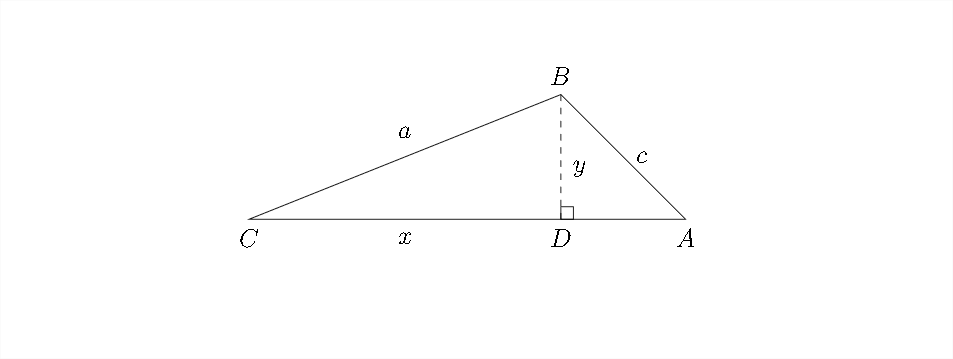
$clipboard_e8074137b0107c3ee6140b3f843274065.png$

Entonces, podemos decir eso$\cos C=\frac{x}{a}$ y que$a \cos C=x$
Si entonces ponemos este triángulo sobre los ejes de coordenadas con$\angle C$ en el origen (0,0) podemos derivar la Ley de los cosenos. La coordenada del vértice en$\angle B$ será$(a \cos C, a \sin C),$ y las coordenadas del vértice en$\angle A$ serán$(b, 0)$

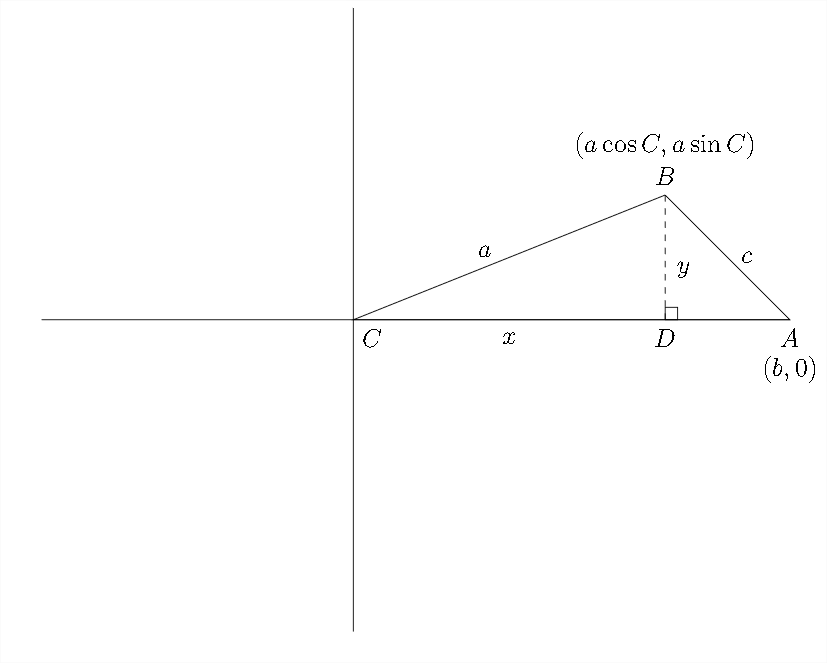
$clipboard_e7b345a04f53ab024c9837562895b59ad.png$

Usando la fórmula de distancia, podemos decir que:
\ [ c=\ sqrt {(a\ cos C-b) ^ {2} + (a\ sin C-0) ^ {2}}
\] Cuadrando ambos lados:
\ [ c^ {2} =( a\ cos C-b) ^ {2} + (a\ sin C-0) ^ {2}
\] y
\ [ c^ {2} =a^ {2}\ cos ^ {2} C-2 a b\ cos C+b^ {2} +a^ {2}\ sin ^ {2} C
\] o
\ [ c^ {2} =a^ {2}\ sin ^ {2} C+a^ {2}\ cos ^ {2} c+b^ {2} -2 a b\ cos C
\]

Factorizando el$a^{2}$ y reemplazando$\sin ^{2} C+\cos ^{2} C$ con 1, salimos con una de las formas más comunes de la Ley de los cosenos:
\ [ \ begin {array} {c}
c^ {2} =a^ {2}\ sin ^ {2} C+a^ {2}\ cos ^ {2} C+b^ {2} -2 a b\ cos C\\
c^ {2} =a^ {2}\ izquierda (\ sin ^ {2} C+\ cos ^ {2} C\ derecha) +b^ {2} -2 a b\ cos C\\
c^ {2} =a^ {2} (1) +b^ {2} -2 a b\ cos C\\
c^ {2} =a^ {2} +b^ {2} -2 a b\ cos C
\ end {array}
\] Cualquier letra puede usarse para representar cada uno de los lados, pero el orden en el que se usan las letras es muy importante. El lado del triángulo aislado en el lado izquierdo debe corresponder al ángulo utilizado en el lado derecho.

La Ley de los cosenos
\ [ \ begin {array} {l}
a^ {2} =b^ {2} +c^ {2} -2 b c\ cos A\\
b^ {2} =a^ {2} +c^ {2} -2 a c\ cos B\
c^ {2} =a^ {2} +b^ {2} -2 a b\ cos C
\ end {array}
\]

Veremos tres ejemplos: dos en los que se dan dos lados y el ángulo incluido y uno en el que se dan los tres lados del triángulo.

Ejemplo 1
Resolver el triángulo: Medidas de ángulo$\angle A=38^{\circ}, c=17, b=8$ redondo y longitudes laterales al más cercano$10^{\text {th }}$.

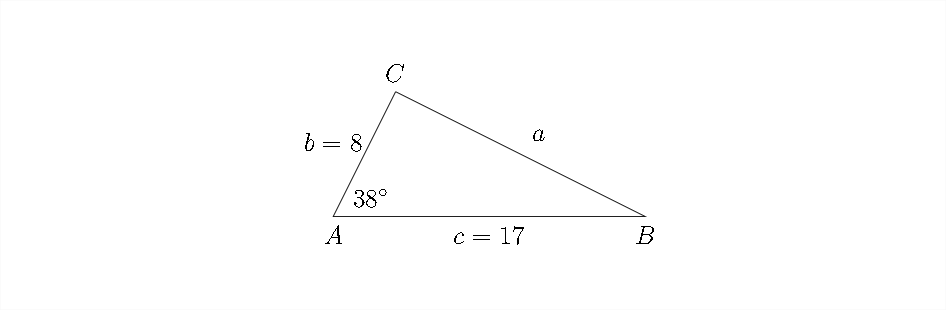
$clipboard_e6f6acd19b3a4c51338653db47eca0ba7.png$

Por lo general, es una buena idea ver si puedes usar primero la Ley de los senos, ya que es más fácil de calcular. En este caso no podemos porque no tenemos un par completo ángulo-lado. Entonces, usando la Ley de cosenos para encontrar lado$a:$
\ [ \ begin {array} {c}
a^ {2} =b^ {2} +c^ {2} -2 b c\ cos A\\
a^ {2} =8^ {2} +17^ {2} -2 * 8 * 17 *\ cos 38^ {\ circ}\\
a^ {2} * aprox 64+289-272 0.7880\\
a^ {2}\ aprox 353-214.336\\
a^ {2}\ aprox 138.664\\
a\ aproximadamente 11.8
\ fin {array}
\]

Una vez que sabemos que$a \approx 11.8$ podemos usar esto para encontrar los otros ángulos usando la Ley de los senos. Por el tema del caso ambiguo al usar la Ley de los senos, a menudo es buena idea encontrar los ángulos que corresponden a los dos lados más cortos del triángulo, porque si hay un ángulo obtuso en el triángulo tendrá que corresponder al lado más largo. Si encontramos los dos ángulos más pequeños, podemos estar seguros de que ambos serán agudos y podemos restarlos$180^{\circ}$ para encontrar el ángulo más grande.

\ [ \ begin {array} {c}
\ frac {\ sin 38^ {\ circ}} {11.8} =\ frac {\ sin B} {8}\\
8\ veces\ frac {0.61566} {11.8} =\ sin B\\
0.4174\ approx\ sin B\\
24.7^ {\ circ}\ approx B
\ end {array}
\] Así con$\angle A=38^{\circ}$ y$\angle B \approx 24.7^{\circ},$ luego:
\ [ \ ángulo C\ aprox 180^ {\ circ} -\ izquierda (38^ {\ circ} +24.7^ {\ circ}\ derecha)\ aproximadamente 180^ {\ circ} -62.7^ {\ circ}\ aproximadamente 117.3^ {\ circ}
\]

Entonces, los ángulos y lados del triángulo serían:
\ [ \ begin {array} {lll}
\ ángulo A=38^ {\ circ} & a\ aproximadamente 11.8\
\ ángulo B\ aproximadamente 24.7^ {\ circ} & b=8\
\ ángulo C\ approx 117.3^ {\ circ} & c=17
\ end {array}
\] En ejemplo$2,$ veremos un problema en el que se da un ángulo obtuso.

Ejemplo 2
Resuelve el triángulo: Medidas de ángulo$\angle A=110^{\circ}, c=30, b=35$ redondo y longitudes laterales al más cercano$10^{\text {th }}$.

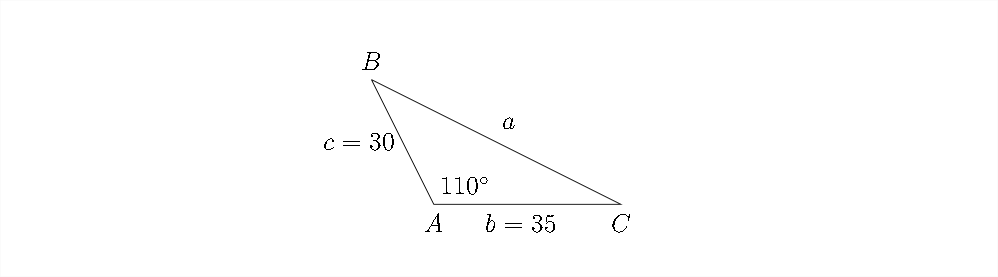
$clipboard_ed8f187ac3be0cfdf1d2de5e1a7e0043b.png$

El cálculo para este problema es ligeramente diferente del último porque el coseno de$110^{\circ}$ será negativo:
\ [ \ begin {array} {c}
a^ {2} =b^ {2} +c^ {2} -2 b c\ cos A\\
a^ {2} =35^ {2} +30^ {2} -2 * 35 * 30 *\ cos 110^ {\ circ}\\
a^ {2}}\ aprox 1225+900-2100 * (-0.3420)\\
a^ {2}\ aprox 2125+718.2\\
a^ {2}\ aproximadamente 2843.2\\
a\ aproximadamente 53.3
\ fin {array}
\]

En este problema, ya que nos dieron un ángulo obtuso, entonces los otros dos ángulos deben ser agudos y no tenemos que preocuparnos por el caso ambiguo en el uso de la Ley de los senos.

\[\frac{\sin 110^{\circ}}{53.3}=\frac{\sin B}{35} \quad \frac{\sin 110^{\circ}}{53.3}=\frac{\sin C}{30}\]

\[35 * \frac{0.9397}{53.3}=\sin B \quad 30 * \frac{0.9397}{53.3}=\sin C\]

\[0.61706 \approx \sin B \quad 0.5289 \approx \sin C\]

\[38.1^{\circ} \approx B \quad 31.9^{\circ} \approx C\]

Entonces los ángulos y lados del triángulo serían:
\ [ \ begin {array} {lll}
\ ángulo A=110^ {\ circ} & a\ aprox 53.3\
\ ángulo B\ aprox 38.1^ {\ circ} & b=35\
\ ángulo C\ aprox 31,9^ {\ circ} & c=30
\ end {array}
\]

En ejemplo$3,$ veremos un problema en el que se dan tres longitudes laterales y encontramos un ángulo usando la Ley de cosenos.
Ejemplo 3
Resolver el triángulo: El ángulo$a=20, \quad c=9, \quad b=15$ redondo mide al más cercano$10^{t h}$

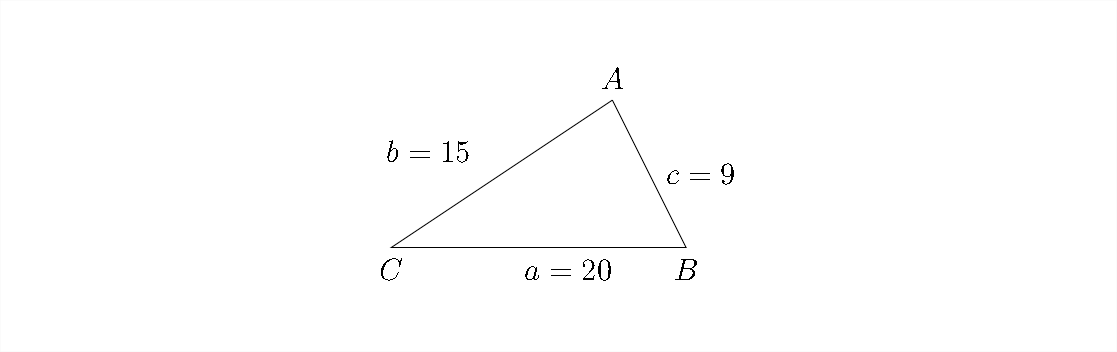
$clipboard_e40710cd88c690b2779cd47b1c2a4eb56.png$

No importa qué ángulo elijamos resolver, pero el ángulo que escojamos debe corresponder al lado aislado en el lado izquierdo de la fórmula. Si queremos resolver por$\angle B,$ diríamos:
\ [ \ begin {array} {c}
b^ {2} =a^ {2} +c^ {2} -2 a c\ cos B\\
15^ {2} =20^ {2} +9^ {2} -2 * 20 * 9 *\ cos B\\
225=400+81-360 *\ cos B\\
225=481-360 cos\\
-256=-360\ cos B\\
\ frac {-256} {-360} =\ frac {-360\ cos B} {-360}\\
0.7\ overline {1} =\ cos B\\
44.7^ {\ circ}\ approx B
\ end {array}
\] Una vez que sepamos la medida de$\angle B,$ usaremos esta para encontrar la medida de la$\angle C,$ cual corresponde a lado $c,$el lado más pequeño. Después restaremos para encontrar el ángulo más grande.
\ [ \ begin {alineado}
\ frac {\ sin 44.7^ {\ circ}} {15} &=\ frac {\ sin C} {9}\\
9 *\ frac {0.7034} {15} &=\ sin C\\
0.42204 &\ approx\ sin C &\
25.0^ {\ circ} &\ approx C
\ final {alineado}
\]

Entonces, con$\angle B \approx 44.7^{\circ}$ y$\angle C \approx 25.0^{\circ},$ luego:
\ [ \ ángulo A\ approx 180^ {\ circ} -\ izquierda (44.7^ {\ circ} +25.0^ {\ circ}\ derecha)\ approx 180^ {\ circ} -69.7^ {\ circ}\ approx 110.3^ {\ circ}
\] Entonces los ángulos y lados del triángulo serían:
\ [ \ begin {array} {lll l}
\ ángulo A=110.3^ {\ circ} & a\ aproximadamente 53.3\
\ ángulo B\ aproximadamente 44.7^ {\ circ} & b=35\\
\ ángulo C\ aprox.25.0^ {\ circ} & c=30
\ end {array}
\]

Si hubiéramos usado la Ley de los senos para encontrar$\angle A$, la calculadora habría devuelto el valor del ángulo de referencia para$\angle A$, ¡en lugar del ángulo que realmente está en el triángulo descrito en el problema!

Ejercicios 4.3
En cada problema, resuelve el triángulo. Redondea las longitudes de los lados al más cercano$100^{\text {th }}$ y el ángulo mide al más cercano$10^{\text {th }}$.

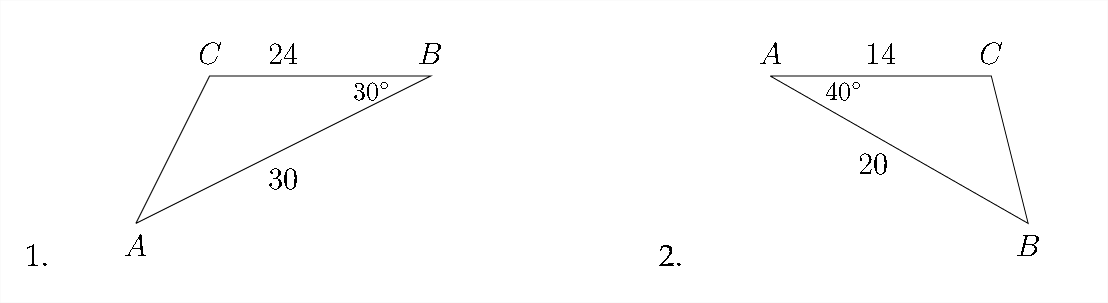
$clipboard_ef84b612c905145a7d7c199ad1b1b1673.png$

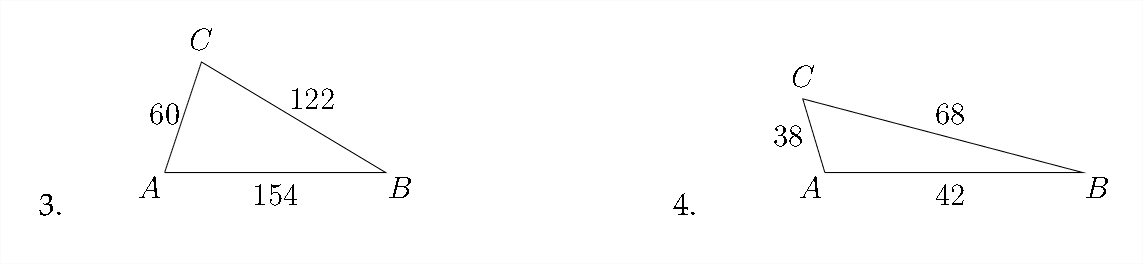
$clipboard_ed2e72f6f63318464e268ba5ee98c2e4c.png$

5. $\quad \angle A=52^{\circ}, \quad c=27, \quad b=36$
6. $\quad \angle B=75^{\circ}, \quad a=32, \quad c=59$
7. $\quad \angle B=135^{\circ}, \quad a=12, \quad c=18$
8. $\quad \angle C=120^{\circ}, \quad b=22, \quad a=30$
9. $\quad a=21, \quad b=26, \quad c=23$
10. $\quad a=11, \quad b=13, \quad c=17$
11. $\quad a=25, \quad b=32, \quad c=40$
12. $\quad a=60, \quad b=88, \quad c=120$
13. $\quad \angle A=77.4^{\circ}, \quad b=444, \quad c=390$
14. $\quad \angle B=10^{\circ}, \quad a=18, \quad c=30$
15. $\quad a=112.7, \quad b=96.5, \quad c=130.2$
16. $\quad a=4.7, \quad b=3.2, \quad c=5.9$