1.6: Funciones de Valor Absoluto
- Page ID
- 121374
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Graficar una función de valor absoluto.
- Resolver una ecuación de valor absoluto.
Hasta la década de 1920, se creía que las llamadas nebulosas espirales eran nubes de polvo y gas en nuestra propia galaxia, a unas decenas de miles de años luz de distancia. Entonces, el astrónomo Edwin Hubble demostró que estos objetos son galaxias por derecho propio, a distancias de millones de años luz. Hoy, los astrónomos pueden detectar galaxias que están a miles de millones de años luz de distancia. Las distancias en el universo se pueden medir en todas las direcciones. Como tal, es útil considerar la distancia como una función de valor absoluto. En esta sección, investigaremos las funciones de valor absoluto.

Comprensión del valor absoluto
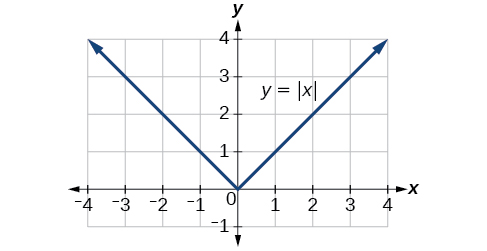
Recordemos que en su forma básica\(f(x)=|x|\), la función de valor absoluto, es una de nuestras funciones de kit de herramientas. La función de valor absoluto se piensa comúnmente como proporcionar la distancia que el número es de cero en una línea numérica. Álgebraicamente, para cualquiera que sea el valor de entrada, la salida es el valor sin tener en cuenta el signo.
Función de Valor Absoluto
La función de valor absoluto se puede definir como una función por partes
\[f(x)=|x|= \begin{cases} x & \text{ if }x{\geq}0 \\ -x & \text{ if } x<0 \end{cases}\]
Ejemplo\(\PageIndex{1}\): Determine a Number within a Prescribed Distance
Describir todos los valores\(x\) dentro o incluyendo una distancia de 4 desde el número 5.
Solución
Queremos que la distancia entre\(x\) y 5 sea menor o igual a 4. Podemos trazar una línea numérica, como la de, para representar la condición a satisfacer.

La distancia de\(x\) a 5 se puede representar usando el valor absoluto como\(|x−5|\). Queremos que los valores de\(x\) que satisfagan la condición\(| x−5 |\leq4\).
Análisis
Tenga en cuenta que
\[\begin{align*} -4&{\leq}x-5 & x-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
Entonces\(|x−5|\leq4\) es equivalente a\(1{\leq}x\leq9\).
Sin embargo, los matemáticos generalmente prefieren la notación de valores absolutos.
Ejercicio\(\PageIndex{1}\)
Describir todos los valores\(x\) dentro de una distancia de 3 del número 2.
- Contestar
-
\(|x−2|\leq3\)
Ejemplo\(\PageIndex{2}\): Resistance of a Resistor
Las partes eléctricas, como resistencias y condensadores, vienen con valores específicos de sus parámetros de funcionamiento: resistencia, capacitancia, etc. Sin embargo, debido a la imprecisión en la fabricación, los valores reales de estos parámetros varían algo de pieza a pieza, incluso cuando se supone que son los mismos. Lo mejor que pueden hacer los fabricantes es intentar garantizar que las variaciones permanezcan dentro de un rango específico, a menudo ± 1%, ± 5% o ± 10%.
Supongamos que tenemos una resistencia nominal de 680 ohmios, ± 5%. Utilice la función de valor absoluto para expresar el rango de valores posibles de la resistencia real.
Solución
El 5% de 680 ohmios es de 34 ohmios. El valor absoluto de la diferencia entre la resistencia real y nominal no debe exceder la variabilidad establecida, por lo que, con la resistencia\(R\) en ohmios,
\[|R−680|\leq34 \nonumber\]
Ejercicio\(\PageIndex{2}\)
Los alumnos que puntúan dentro de los 20 puntos de 80 pasarán una prueba. Escribe esto como una distancia desde 80 usando notación de valor absoluto.
- Contestar
-
Usando la variable\(p\) para pasar,\(| p−80 |\leq20\)
Graficar una función de valor absoluto
La característica más significativa de la gráfica de valor absoluto es el punto de esquina en el que la gráfica cambia de dirección. Este punto se muestra en el origen en la Figura\(\PageIndex{3}\).
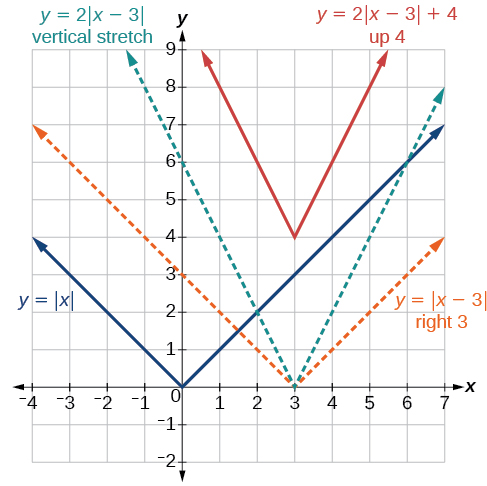
En la figura se\(\PageIndex{3}\) muestra la gráfica de\(y=2|x–3|+4\). La gráfica de\(y=|x|\) ha sido desplazada hacia la derecha 3 unidades, estirada verticalmente por un factor de 2, y desplazada hacia arriba 4 unidades. Esto significa que el punto de esquina se encuentra en\((3,4)\) para esta función transformada.
Ejemplo\(\PageIndex{3}\): Writing an Equation for an Absolute Value Function
Escribe una ecuación para la función graficada en la Figura\(\PageIndex{5}\).
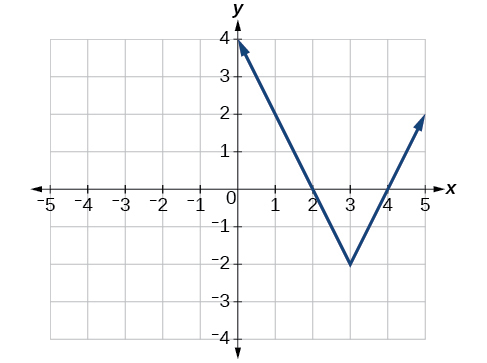
Solución
La función de valor absoluto básico cambia de dirección en el origen, por lo que esta gráfica se ha desplazado hacia la derecha 3 unidades y hacia abajo 2 unidades desde la función básica del kit de herramientas. Ver Figura\(\PageIndex{6}\).
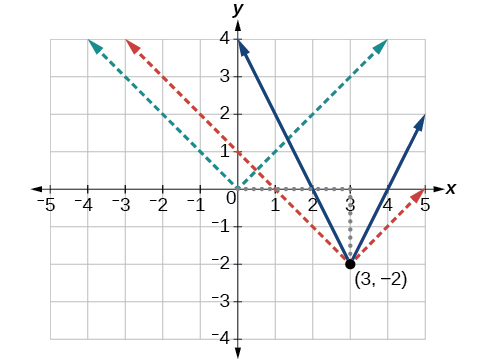
También notamos que la gráfica aparece estirada verticalmente, debido a que el ancho de la gráfica final sobre una línea horizontal no es igual a 2 veces la distancia vertical desde la esquina hasta esta línea, como lo sería para una función de valor absoluto sin estirar. En cambio, el ancho es igual a 1 veces la distancia vertical como se muestra en la Figura\(\PageIndex{7}\).
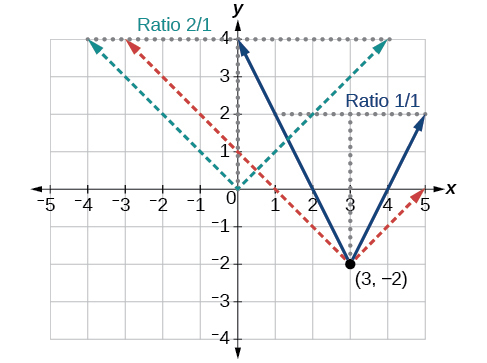
A partir de esta información podemos escribir la ecuación
\[\begin{align*} f(x)&=2|x-3|-2, \;\;\;\;\;\; \text{treating the stretch as a vertial stretch, or} \\ f(x)&=|2(x-3)|-2, \;\;\; \text{treating the stretch as a horizontal compression.} \end{align*}\]
Análisis
Tenga en cuenta que estas ecuaciones son algebraicamente equivalentes: el estiramiento para una función de valor absoluto se puede escribir indistintamente como estiramiento o compresión vertical u horizontal.
Q & A
Si no pudiéramos observar el tramo de la función a partir de las gráficas, ¿podríamos determinarla algebraicamente?
- Contestar
-
Sí. Si no podemos determinar el estiramiento en función del ancho de la gráfica, podemos resolver el factor de estiramiento poniendo un par de valores conocidos para\(x\) y\(f(x)\).
\[f(x)=a|x−3|−2 \nonumber\]
Ahora sustituyendo en el punto\((1, 2)\)
\[\begin{align*} 2&=a|1-3|-2 \\ 4&=2a \\ a&=2 \end{align*}\]
Ejercicio\(\PageIndex{3}\)
Escribe la ecuación para la función de valor absoluto que se desplaza horizontalmente a la izquierda 2 unidades, se voltea verticalmente y se desplaza verticalmente hacia arriba 3 unidades.
- Contestar
-
\(f(x)=−| x+2 |+3\)
Q & A
¿Las gráficas de las funciones de valor absoluto siempre se cruzan con el eje vertical? ¿El eje horizontal?
- Contestar
-
Sí, siempre se cruzan con el eje vertical. La gráfica de una función de valor absoluto cruzará el eje vertical cuando la entrada sea cero.
No, no siempre se cruzan con el eje horizontal. La gráfica puede o no intersectar el eje horizontal, dependiendo de cómo se haya desplazado y reflejado la gráfica. Es posible que la función de valor absoluto interseccione el eje horizontal en cero, uno o dos puntos (Figura\(\PageIndex{8}\)).
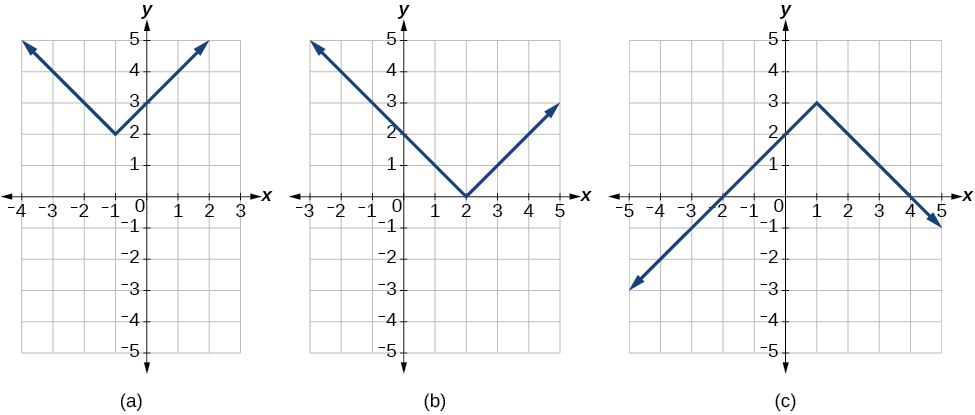
Figura\(\PageIndex{8}\): (a) La función de valor absoluto no intersecta el eje horizontal. (b) La función de valor absoluto cruza el eje horizontal en un punto. (c) La función de valor absoluto cruza el eje horizontal en dos puntos.
Resolver una ecuación de valor absoluto
Ahora que podemos graficar una función de valor absoluto, aprenderemos a resolver una ecuación de valor absoluto. Para resolver una ecuación como\(8=|2x−6|\), notamos que el valor absoluto será igual a 8 si la cantidad dentro del valor absoluto es 8 o -8. Esto lleva a dos ecuaciones diferentes que podemos resolver de forma independiente.
\[2x-6=8 \quad \text{ or } \quad 2x-6=-8 \nonumber\]
\[\begin{align*} 2x &= 14 & 2x &= -2 \\ x&=7 & x&=-1 \end{align*}\]
Saber resolver problemas que involucran funciones de valor absoluto es útil. Por ejemplo, es posible que necesitemos identificar números o puntos en una línea que estén a una distancia especificada de un punto de referencia dado.
Una ecuación de valor absoluto es una ecuación en la que la variable desconocida aparece en barras de valor absoluto. Por ejemplo,
\[\begin{align*}|x|&=4, \nonumber \\[4pt] |2x−1| &=3, \\[4pt] |5x+2|−4 &=9. \end{align*}\]
Soluciones a Ecuaciones de Valor Absoluto
Para números reales\(A\) y\(B\), una ecuación de la forma\(|A|=B\), con\(B\geq0\), tendrá soluciones cuando\(A=B\) o\(A=−B\). Si\(B<0\), la ecuación no\(|A|=B\) tiene solución.
Cómo...
Dada la fórmula para una función de valor absoluto, encuentra las intercepciones horizontales de su gráfica.
- Aísle el término del valor absoluto.
- Utilizar\(|A|=B\) para escribir\(A=B\) o\(−A=B\), asumiendo\(B>0\).
- Resolver para\(x\).
Ejemplo\(\PageIndex{4}\): Finding the Zeros of an Absolute Value Function
Para la función\(f(x)=|4x+1|−7\), encuentra los valores de\(x\) tal que\(f(x)=0\).
Solución
\[\begin{align*} 0&=|4x+1|-7 & & &\text{Substitute 0 for f(x).} \\ 7&=|4x+1| & & &\text{Isolate the absolute value on one side of the equation.} \\ 7&=4x+1 &\text{or} -7&=4x+1 &\text{Break into two separate equations and solve.} \\ 6&=4x & -8&=4x & \\ x&=\frac{6}{4}=1.5 & x&=\frac{-8}{4}=-2 \end{align*}\]
La función emite 0 cuando\(x=1.5\) o\(x=−2\) (Figura\(\PageIndex{9}\)).
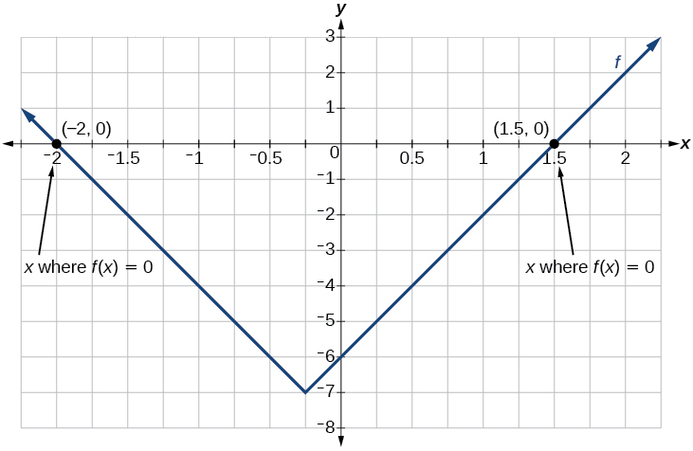
Ejercicio\(\PageIndex{4}\)
Para la función\(f(x)=|2x−1|−3\), encuentra los valores de\(x\) tal que\(f(x)=0\).
Solución
\(x=−1\)o\(x=2\)
Q & A
¿Deberíamos esperar siempre dos respuestas a la hora de resolver\(|A|=B\)?
Contestar
No. Podemos encontrar una, dos, o incluso ninguna respuesta. Por ejemplo, no hay solución para\(2+|3x−5|=1\).
Cómo...
Dada una ecuación de valor absoluto, resolverla.
- Aísle el término del valor absoluto.
- \(|A|=B\)Utilízalo para escribir\(A=B\) o\(A=−B\).
- Resolver para\(x\).
Ejemplo\(\PageIndex{5}\): Solving an Absolute Value Equation
Resolver\(1=4|x−2|+2\).
Solución
Aislar el valor absoluto en un lado de la ecuación da lo siguiente.
\[\begin{align*} 1&=4|x-2|+2 \\ -1&=4|x-2| \\ -\frac{1}{4}&=|x-2| \end{align*}\]
El valor absoluto siempre devuelve un valor positivo, por lo que es imposible que el valor absoluto sea igual a un valor negativo. En este punto, notamos que esta ecuación no tiene soluciones.
Q & A
En Ejemplo\(\PageIndex{5}\), si\(f(x)=1\) y\(g(x)=4|x−2|+2\) fueran graficados en el mismo conjunto de ejes, ¿se cruzarían las gráficas?
Contestar
No. Las gráficas de\(f\) y no se\(g\) cruzarían, como se muestra en la Figura\(\PageIndex{10}\). Esto confirma, gráficamente, que la ecuación no\(1=4|x−2|+2\) tiene solución.
Encuentra donde la gráfica de la función\(f(x)=−| x+2 |+3\) intersecta los ejes horizontal y vertical.
\(f(0)=1\), por lo que la gráfica cruza el eje vertical en\((0,1)\). \(f(x)=0\)cuando\(x=−5\) y\(x=1\) así la gráfica cruza el eje horizontal en\((−5,0)\) y\((1,0)\).
Resolviendo una desigualdad de valor absoluto
Las ecuaciones de valores absolutos no siempre pueden implicar igualdades. En cambio, es posible que necesitemos resolver una ecuación dentro de un rango de valores. Usaríamos una desigualdad de valor absoluto para resolver tal ecuación. Una desigualdad de valor absoluto es una ecuación de la forma
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
o
\[ |A|{\geq}B, \nonumber\]
donde una expresión\(A\) (y posiblemente pero no usualmente\(B\)) depende de una variable\(x\). Resolver la desigualdad significa encontrar el conjunto de todos los\(x\) que satisfagan la desigualdad. Por lo general, este conjunto será un intervalo o la unión de dos intervalos.
Existen dos enfoques básicos para resolver las desigualdades de valores absolutos: gráfica y algebraica. La ventaja del enfoque gráfico es que podemos leer la solución interpretando las gráficas de dos funciones. La ventaja del enfoque algebraico es que produce soluciones que pueden ser difíciles de leer de la gráfica.
Por ejemplo, sabemos que todos los números dentro de las 200 unidades de 0 pueden expresarse como
\[|x|<200 \nonumber\]
o
\[ −200<x<200 \nonumber\]
Supongamos que queremos conocer todos los posibles rendimientos de una inversión si pudiéramos ganar alguna cantidad de dinero dentro de $200 de $600. Podemos resolver algebraicamente para el conjunto de valores de\(x\) tal manera que la distancia entre\(x\) y 600 sea menor a 200. Representamos la distancia entre\(x\) y 600 como\(|x−600|\).
\[|x−600|<200\]
o
\[−200<x−600<200\]
\[\begin{align*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \end{align*}\]
Esto significa que nuestras devoluciones estarían entre $400 y $800.
A veces se nos presentará un problema de desigualdad de valor absoluto en términos de una función de valor absoluto desplazada y/o estirada o comprimida, donde debemos determinar para qué valores de la entrada la salida de la función será negativa o positiva.
Cómo...
Dada una desigualdad de valor absoluto de la forma\(|x−A|{\leq}B\) para números reales\(a\) y\(b\) donde\(b\) es positiva, resolver la desigualdad de valor absoluto algebraicamente.
- Encuentra puntos de límite resolviendo\(|x−A|=B\).
- Intervalos de prueba creados por los puntos de límite para determinar dónde\(|x−A|{\leq}B\).
- Escriba el intervalo o unión de intervalos que satisfagan la desigualdad en la notación de intervalo, desigualdad o constructor de conjuntos.
Ejemplo\(\PageIndex{6}\): Solving an Absolute Value Inequality
Resolver\(|x −5|{\leq}4\).
Solución
Con ambos enfoques, necesitaremos saber primero dónde es verdadera la igualdad correspondiente. En este caso primero encontraremos dónde\(|x−5|=4\). Hacemos esto porque el valor absoluto es una función sin cortes, por lo que la única forma en que los valores de la función pueden pasar de ser menores de 4 a ser mayores que 4 es pasando por donde los valores son iguales a 4. Resolver\(|x−5|=4\).
\[\begin{align*} x−5&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−5&=−4 & x&=1\end{align*}\]
Después de determinar que el valor absoluto es igual a 4 at\(x=1\) y\(x=9\), sabemos que la gráfica sólo puede cambiar de ser menor de 4 a mayor de 4 en estos valores. Esto divide la línea numéricahasta en tres intervalos:
\[x<1,\; 1<x<9, \text{ and } x>9. \nonumber\]
Para determinar cuándo la función es menor que 4, podríamos elegir un valor en cada intervalo y ver si la salida es menor o mayor que 4, como se muestra en la Tabla\(\PageIndex{1}\).
| Prueba de intervalos\(x\) | \(f(x)\) | \(<4\)o\(>4\) | |
|---|---|---|---|
| \ (x\)” style="vertical-align:middle; ">\(x<1\) | \ (f (x)\)” style="vertical-align:middle; ">0 | \ (<4\) o\(>4\) "style="vertical-align:middle;" >\(|0-5|=5\) | Mayor que |
| \ (x\)” style="vertical-align:middle; ">\(1<x<9\) | \ (f (x)\)” style="vertical-align:middle; ">6 | \ (<4\) o\(>4\) "style="vertical-align:middle;" >\(|6-5|=1\) | Menos de |
| \ (x\)” style="vertical-align:middle; ">\(x>9\) | \ (f (x)\)” style="vertical-align:middle; ">11 | \ (<4\) o\(>4\) "style="vertical-align:middle;" >\(|11-5|=6\) | Mayor que |
Debido a que\(1{\leq}x{\leq}9\) es el único intervalo en el que la salida en el valor de prueba es menor que 4, podemos concluir que la solución a\(|x−5|{\leq}4\) es\(1{\leq}x{\leq}9\), o\([1,9]\).
Para usar una gráfica, podemos bosquejar la función\(f(x)=|x−5|\). Para ayudarnos a ver dónde están las salidas 4, también se\(g(x)=4\) podría esbozar la línea como en la Figura\(\PageIndex{11}\).
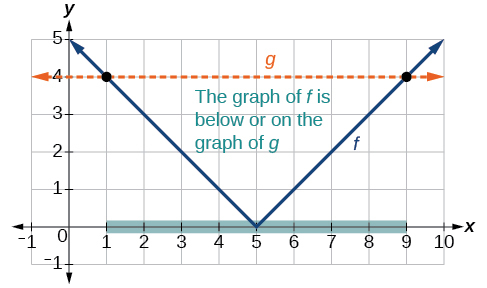
Podemos ver lo siguiente:
- Los valores de salida del valor absoluto son iguales a 4 at\(x=1\) y\(x=9\).
- La gráfica de\(f\) está debajo de la gráfica de\(g\) on\(1<x<9\). Esto significa que los valores de salida de\(f(x)\) son menores que los valores de salida de\(g(x)\).
- El valor absoluto es menor o igual a 4 entre estos dos puntos, cuando\(1{\leq}x\leq9\). En notación de intervalos, este sería el intervalo\([1,9]\).
Análisis
Para las desigualdades de valor absoluto,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; x−A<−C \text{ or } x−A>C. \nonumber\]
El\(>\) símbolo\(<\) o puede ser sustituido por\(\leq\) o\(\geq\).
Entonces, para este ejemplo, podríamos usar este enfoque alternativo.
\[\begin{align*} |x−5|&{\leq}4 \\ −4&{\leq}x−5{\leq}4 &\text{Rewrite by removing the absolute value bars.} \\ −4+5&{\leq}x−5+5{\leq}4+5 &\text{Isolate the x.} \\ 1&{\leq}x\leq9 \end{align*}\]
Ejercicio\(\PageIndex{5}\)
Resolver\(|x+2| \leq 6\).
- Contestar
-
\(-8 \leq x \leq 4\)
Cómo...
Dada una función de valor absoluto, resuelve para el conjunto de entradas donde la salida es positiva (o negativa).
- Establezca la función igual a cero y resuelva los puntos límite del conjunto de soluciones.
- Utilice puntos de prueba o una gráfica para determinar dónde la salida de la función es positiva o negativa.
Ejemplo\(\PageIndex{7}\): Using a Graphical Approach to Solve Absolute Value Inequalities
Dada la función\(f(x)=−\frac{1}{2}|4x−5|+3\), determinar los\(x\) -valores para los cuales los valores de la función son negativos.
Solución
Estamos tratando de determinar dónde\(f(x)<0\), cuál es cuándo\(−\frac{1}{2}|4x−5|+3<0\). Comenzamos aislando el valor absoluto.
\[ \begin{align*} -\frac{1}{2}|4x−5|&<−3 \;\;\; \text{Multiply both sides by –2, and reverse the inequality.} \\ |4x−5|&>6\end{align*}\]
A continuación resolvemos por la igualdad\(|4x−5|=6\).
\[\begin{align*} 4x-5&=6 & 4x-5&=-6 \\ 4x-6&=6 \end{align*}\]
o
\[\begin{align*} 4x&=-1 \\ x&=\frac{11}{4} & x&=-\frac{1}{4} \end{align*}\]
Ahora, podemos examinar la gráfica de\(f\) para observar donde la salida es negativa. Observaremos dónde están las ramas por debajo del\(x\) eje -eje. Observe que ni siquiera es importante exactamente cómo se ve la gráfica, siempre y cuando sepamos que cruza el eje horizontal en\(x=−\frac{1}{4}\) y\(x=\frac{11}{4}\) y que la gráfica se ha reflejado verticalmente. Ver Figura\(\PageIndex{12}\).
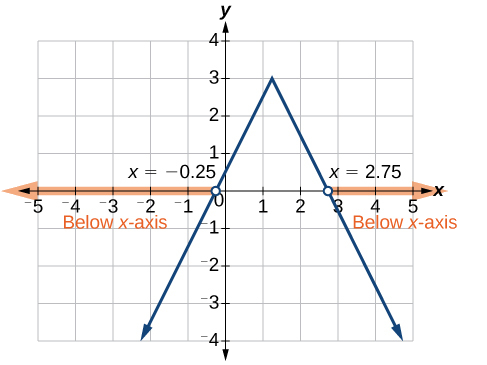
Observamos que la gráfica de la función está por debajo del\(x\) eje -izquierda\(x=−\frac{1}{4}\) y derecha de\(x=\frac{11}{4}\). Esto significa que los valores de la función son negativos a la izquierda de la primera intercepción horizontal en\(x=−\frac{1}{4}\), y negativos a la derecha de la segunda intercepción en\(x=\frac{11}{4} \). Esto nos da la solución a la desigualdad.
\[x<−\frac{1}{4} \text{ or } x>1\frac{1}{4} \nonumber\]
En notación de intervalos, esto sería\(( −\infty,−0.25 )\cup( 2.75,\infty)\).
Ejercicio\(\PageIndex{6}\)
Resolver\(−2|k−4|\leq−6\).
- Contestar
-
\(k\leq1\)o\(k\geq7\); en notación de intervalos, esto sería\(\left(−\infty,1\right]\cup\left[7,\infty\right)\)
Conceptos clave
- La función de valor absoluto se usa comúnmente para medir distancias entre puntos.
- Los problemas aplicados, como rangos de valores posibles, también se pueden resolver usando la función de valor absoluto.
- La gráfica de la función de valor absoluto se asemeja a una letra V. Tiene un punto de esquina en el que la gráfica cambia de dirección.
- En una ecuación de valor absoluto, una variable desconocida es la entrada de una función de valor absoluto.
- Si el valor absoluto de una expresión se establece igual a un número positivo, espere dos soluciones para la variable desconocida.
- Una ecuación de valor absoluto puede tener una solución, dos soluciones o ninguna solución.
- Una desigualdad de valor absoluto es similar a una ecuación de valor absoluto pero toma la forma | A |B<B, | A |≤B, | A |>, o | A |≥B.Se puede resolver determinando los límites del conjunto de soluciones y luego probando qué segmentos están en el conjunto.
- Las desigualdades de valores absolutos también se pueden resolver gráficamente.
Glosario
ecuación de valor absoluto
una ecuación de la forma\(|A|=B\), con\(B\geq0\); tendrá soluciones cuando\(A=B\) o\(A=−B\)
desigualdad de valor absoluto
una relación en la forma\(|A|<B\),\(|A|{\leq}B\),\(|A|>B\), o\(|A|{\geq}B\)


